贝叶斯统计分析的新工具— Stan*

刘 晋 汪秀琴 李天萍 徐文华 陈 峰

【提 要】 目的 鉴于国内研究者熟悉的贝叶斯统计软件WinBUGS已停止更新，OpenBUGS已见介绍，本文介绍国外新近出现的贝叶斯统计软件Stan的基本原理与实际使用。方法 由于Stan安装具有其自身特点且较为复杂，本文首先介绍Windows平台下Stan安装与使用方法，接着介绍Stan语言及运行步骤，最后以线性-正态层次模型为例介绍Stan的应用。结果 Stan作为一种新型贝叶斯统计软件，使用了全新的汉密尔顿蒙托卡罗(Hamiltonian Monte Carlo，HMC)抽样方法，可以处理GIBBS抽样难以收敛的复杂多元层次模型。Stan使用的概率模型定义语言，相比较BUGS，逻辑清晰，程序更易理解。结论 Stan功能强大，应用方便，是贝叶斯分析的有力工具。

贝叶斯统计历史悠久，与频率统计并称统计学的两大学派。自Tomas Bayes提出贝叶斯定理至今已有300余年，直到近30年，马尔科夫链-蒙托卡罗(Markov Chain Monto Carlo，MCMC)模拟技术以及计算机技术的迅速发展使计算后验分布高维积分的难题得以解决，贝叶斯统计才在理论与应用上得以快速发展。各类基于MCMC的贝叶斯统计软件的出现，将研究者从复杂繁琐的后验分布计算中解脱出来，从而更专注于贝叶斯模型本身，非统计专业人员也能将贝叶斯统计应用于相应领域。可以说，贝叶斯统计软件对贝叶斯统计理论和应用的发展起到了重要作用。

目前国际上常用的贝叶斯统计软件有BUGS(WinBUGS、OpenBUGS)、JAGS、Stan及多种R软件包[1-3]。国内对WinBUGS软件有较为详尽的介绍[4-9]，但该软件已于2007年停止更新。最近对该软件的发展版OpenBUGS已见介绍[10-13]。而Stan是近年新出现的贝叶斯统计软件，与BUGS等贝叶斯统计软件相比，Stan具有应用平台广、复杂模型下计算速度快、语言更加灵活的特点，在国外已受到广泛关注。如贝叶斯统计的著名学者Andrew Gelman使用Stan作为其著作的例子[2]，Kruschke在其介绍贝叶斯统计分析的著作中将Stan作为示例软件之一[1]。这些动向说明Stan正成为贝叶斯分析工具的新选择，但国内尚未见相关研究。

Stan软件基本情况

Stan是一款基于C++语言编写的采用MCMC方法对复杂统计模型进行贝叶斯推断的专业工具。它是开源软件，可从https://mc-stan.org/免费下载，使用者也可根据自身需求，编写函数，扩展其功能。该软件可在Windows、Mac OS、Linux 3种操作系统下运行，通过R、Python等6款统计软件调用。与BUGS、JAGS主要使用Gibbs抽样不同，Stan使用的是汉密尔顿蒙托卡罗(Hamiltonian Monte Carlo，HMC)抽样，在复杂模型的条件下，HMC的抽样较GIBBS抽样效率更高。本文将以Windows环境下，使用R调用Stan为例，介绍Stan的使用方法。其它平台以及软件下的Stan使用方法，可以参考Stan官网帮助[14]。

Stan的运行可分为以下6个步骤：(1)使用Stan概率模型语言，建立贝叶斯统计模型；(2)通过Stanc函数将Stan模型语言编译为C++代码；(3)将C++代码编译为可以被R载入的动态链接库；(4)运行动态链接库的程序从后验分布中抽样；(5)对后验分布样本进行收敛诊断；(6)基于后验分布进行统计推断。

通常，(2)至(4)步可从R中调用函数来实现，使用者不需要了解其中具体过程，但是如需对程序进行调试，也可以逐步执行(2)、(3)、(4)步。下文将介绍Stan软件的安装与具体使用过程。

Stan软件安装与使用

与BUGS等贝叶斯统计软件相比，Stan的安装具有其自身特点且较为复杂，本部分将介绍Windows平台下，基于R界面的Stan安装与使用方法。

R界面下的Stan软件是名为RStan的R软件包。截至本文写作时,其最新版本是发布于2018年11月9日的2.18.2。

1.安装

首先安装R软件，从https://www.r-project.org/下载，版本要求为3.4.0或更新。

RStan安装前，为确保R中没有RStan，在R中运行以下命令以清除原有RStan：

remove.packages("rstan")

if (file.exists(".RData")) file.remove(".RData")

重启R，安装rstan包。运行以下命令：

install.packages("rstan",repos="https://cloud.r-project.org/",dependencies=TRUE)

检查C++ 工具链安装情况,运行以下命令：

pkgbuild::has_build_tools(debug=TRUE)

如包含C++工具链的Rtools软件尚未安装，根据提示，从http://cran.r-project.org/bin/windows/Rtools/下载并安装。注意在安装过程中，需要勾选“add rtools to system Path”选项。

Rtools安装完成后，为确认其安装成功，重新运行命令：pkgbuild::has_build_tools(debug=TRUE)，如返回如图1结果“TRUE”代表安装成功。

载入rstan包，运行如下命令：library(rstan)，R显示结果见图2。

图2提示运行如下三条命令以充分使用计算机CPU与内存，保存已经编译的程序等，目的是加快stan程序的运行速度。这三条命令如不运行，也不影响使用。

options(mc.cores=parallel::detectCores())

rstan_options(auto_write=TRUE)

Sys.setenv(LOCAL_CPPFLAGS='-march=native')

图1 rstan安装成功提示

图2 rstan性能优化配置提示

至此，rstan的安装与配置工作结束。

2.Stan语言及应用

Stan语言是一种概率程序语言，一个完整的Stan程序一般由若干个模块构成，包括数据模块(data)、参数模块(parameters)、参数转换模块(transformed parameters)、模型模块(model)、预测值模块(generated quantities)。在各模块内，可以定义变量、使用赋值语句、函数以及表达式等元素。数据模块的作用是定义构建贝叶斯模型的观察变量类型、取值范围等；参数模块定义贝叶斯模型参数的类型、取值范围；参数转换模块通过表达式与赋值语句将参数模块的参数转换为新的参数变量；模型模块通过对观察变量指定特定的概率分布函数定义似然函数；预测值模块通过变量定义与赋值语句定义预测变量。

值得指出的是，与BUGS语言不同，Stan程序是基于C++语言的，因此，各变量使用前必须定义，各模块需按照顺序排列。

以OpenBUGS软件示例第一卷第一个例子为例[15]，部分数据示例见表 1。欲了解小鼠日龄与体重的关系。以日龄作为自变量，体重作为因变量。构建线性-正态层次模型。

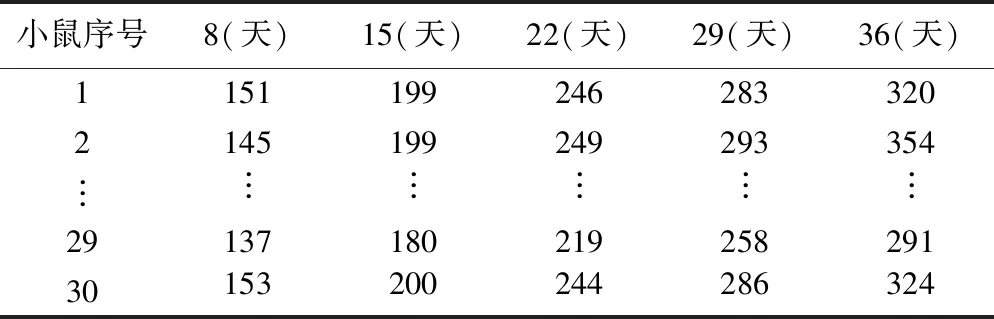
表1 小鼠成长数据示例

构建贝叶斯模型如下：

似然函数：yij～N(ai+βi(xij-xbar),σy)

层次先验：

第一层：αi～N(μα,σα)β～N(μβ,σβ)

第二层：σy,σs,σβ～IG(0.001,0.001),μα,μβ～N(0,100)

y代表小鼠体重，x代表小鼠日龄，下标i代表第i只小鼠，下标j代表第j天，xbar为30只小鼠5次测量体重的均值。感兴趣的变量是各小鼠体重随年龄变化的平均水平βα、基线下的小鼠平均体重α0=μα-μβxbar。

步骤1 定义Stan，构建模型

在文本编辑器中使用Stan语法定义贝叶斯模型，以“Stan”后缀存储，本例所用的Stan程序如下。

data {

intN;//定义总样本量为N，类型为整数，下限为0。

intT;//定义体重测量次数为T，类型为整数，下限为0。

real x[T];//定义年龄为x，类型为实向量

real y[N,T];//定义体重为y，类型为实矩阵

real xbar;//定义体重均值为xbar,类型为实数

}

parameters {

real alpha[N];//定义参数α，类型为实向量，向量长度为N

real beta[N]; //定义参数β，类型为实向量，向量长度为N

real mu_alpha;//定义超参数μα，类型为实数

real mu_beta; // 定义超参数μβ，类型为实数

}

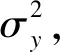
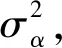
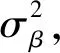
transformed parameters {

realsigma_y; //定义参数σy,类型为实数，下限为0

realsigma_alpha;//定义参数σα，类型为实数，下限为0

realsigma_beta; //定义参数σβ，类型为实数，下限为0

}

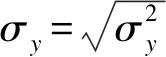
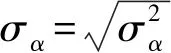
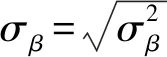
model {

mu_alpha ～ normal(0,100);//定义μα先验分布为一扁平的正态分布

mu_beta ～ normal(0,100);//定义μβ先验分布为一扁平的正态分布

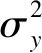
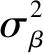
alpha ～ normal(mu_alpha,sigma_alpha); // 定义向量α的每个参数先验分布服从正态分布

beta ～ normal(mu_beta,sigma_beta); //定义向量β的每个参数先验分布服从正态分布

for (n in 1:N)

for (t in 1:T)

y[n,t] ～ normal(alpha[n] + beta[n]*(x[t]-xbar),sigma_y);

}//利用循环定义线性正态分布似然函数

generated quantities {

real alpha0;//定义α0类型为实数

alpha0 <- mu_alpha - xbar * mu_beta;//为α0赋值

}

本程序涵盖了上文介绍的Stan语句模块。结合注释，应不难理解程序的含义。在参数模块中指定的参数为方差，再通过参数转换模块将其变换为标准差，是出于提高软件运行效率的考虑。

步骤2 数据准备

数据以R列表(list)形式存储，其中x为小鼠的日龄，xbar为日龄均值，N为小鼠数目，T为观察次数，y为小鼠体重。

rats_data <- list(x=c(8.0,15.0,22.0,29.0,36.0),xbar=22,N=30,T=5,y=structure(

.Data=c(151,199,246,283,320,

145,199,249,293,354,

……

137,180,219,258,291,

153,200,244,286,324),

.Dim=c(30,5)))

步骤3 后验分布抽样

通过library语句载入rStan软件包，并通过Stan函数执行HMC抽样，结果存储于fit_rats变量，该变量存储了模型构建以及后验样本等信息，后续的收敛诊断以及统计推断的数据均来自于该变量。该变量存储初始值、Stan函数的参数设置、Stan模型、以及后验分布抽样样本等信息。执行HMC抽样的语句为

library(rStan)

fit_rats <- Stan(

file="C: ats.Stan",# Stan程序

data=rats_data,# 存储数据的列表名称

chains=4, # 马尔科夫链数目

warmup=1000, # 预热迭代次数

iter=5000 # 每条链的迭代次数

)

步骤4 收敛诊断

通过traceplot函数可以对估计参数绘制踪迹图，以对后验样本是否收敛进行诊断，图3显示了4个参数的踪迹图，并用灰色表示预热状态的抽样。

traceplot(fit_rats,pars=c("alpha0","mu_beta","mu_alpha","sigma_y"),inc_warmup=TRUE,nrow=4)

由图3可见，在抽样250次后，4条马尔科夫链很好的重合在一起，并保持平稳、水平。说明模型已经很好的收敛，更多的收敛诊断方法可以使用Stan提供的bayesplot软件包进行收敛诊断。

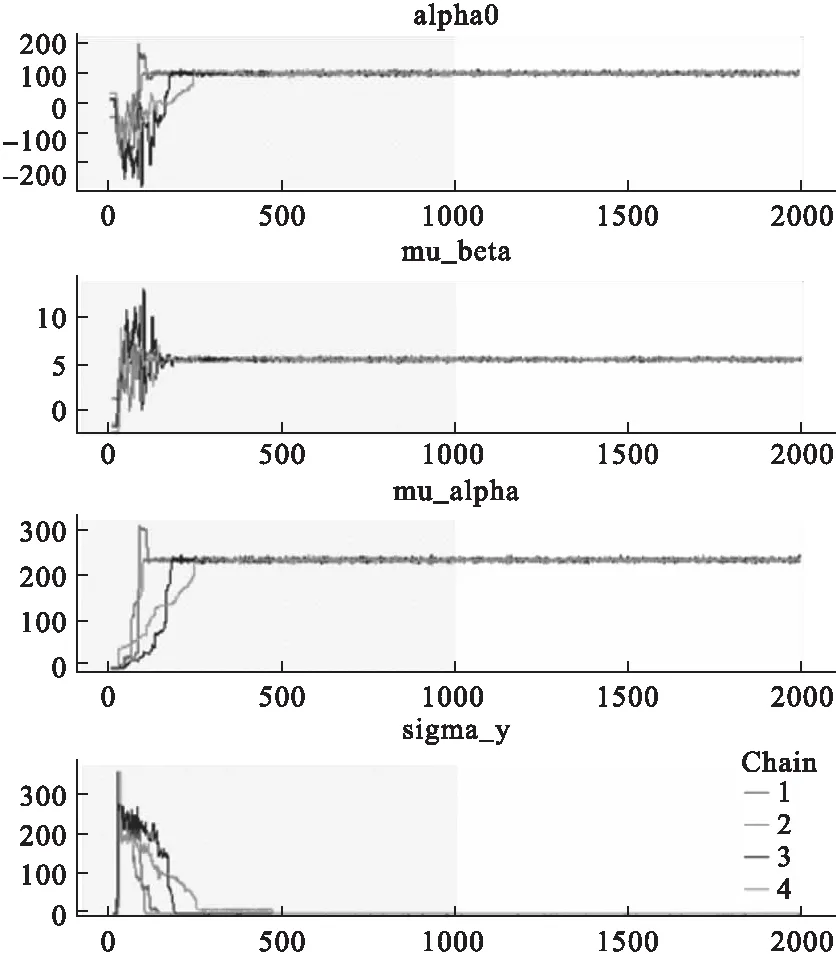
图3 各参数后验分布收敛情况

步骤5 后验分布推断

使用print 函数展示后验样本的统计推断结果，可通过指定pars参数指定需要展示的变量参数，本例展示α0、μβ、μα、σy4个参数的后验分布推断结果。

print(fit_rats,pars=c("alpha0","mu_beta","mu_alpha","sigma_y"),probs=c(0.05,0.5,0.95))

讨 论

本文介绍了Stan在Windows下通过R软件进行贝叶斯统计建模与推断的基本功能。该软件也可采用其它方式调用，如命令行以及matalab、python等软件。通过Stan_demo()函数，使用者可以利用Stan运行和BUGS相同的应用示例。同时，Stan官网也提供软件详细的说明文档以及Stan应用的文献。从使用便利性来讲，Stan作为R的一个软件包，与R深度融合。可以利用R软件丰富的函数和工具包进行数据的读取、整理以及进一步分析，极大的扩展了该软件的功能。例如，通过ShinyStan软件包，可以在浏览器界面对分析结果进行统计、图形展示并提供了5种收敛诊断方法。通过Bayesplot软件包，也可以进行收敛诊断并绘制各种图形。通过LOO软件包可以进行留一法交叉验证，并计算误差。同时，与R的结合使得Stan适合进行大规模的贝叶斯统计模拟。虽然OpenBUGS通过R2Bugs软件包也可以实现在R中的调用，但是，它是通过外部调用实现的，当需要进行大规模模拟时，速度不如Stan。其次，与BUGS、JAGS等软件相比，Stan使用了全新的HMC抽样方法，可以处理GIBBS抽样难以收敛的复杂多元层次模型。Stan使用的概率模型定义语言大体与BUGS类似，不同之处是，变量使用前必须事先定义，语句按顺序执行。因此与BUGS比较，则程序逻辑更为清晰，易于理解。

表2 各参数后验推断

当然，与BUGS相比，Stan的安装过程略显繁琐，同时需要使用者掌握一定的R软件知识。定义模型未提供图形化的操作界面，也不能以BUGS软件有向图的方式定义贝叶斯模型。但总体而言，安装与掌握该软件的使用难度并不大，同时其官网提供了详细的文字与视频教程，以及丰富的应用实例，对于BUGS软件的实例，均有对应的例子提供。相信初学者通过学习这些资料，可以很快掌握该软件的使用方法。通过本文的介绍，希望能够推动Stan软件在国内的应用，利用Stan软件的强大功能，使贝叶斯统计在医学研究中发挥更大作用。