催化效应对气动热环境影响的流动-传热耦合数值分析

王国林, 周印佳, 金 华, 孟松鹤

(1. 哈尔滨工业大学 特种环境复合材料技术国家级重点实验室, 哈尔滨 150080; 2. 中国空气动力研究与发展中心 超高速空气动力研究所, 四川 绵阳 621000; 3. 中国空间技术研究院 载人航天总体部, 北京 100010)

0 引 言

几十年来，考虑复杂结构和各种防热材料的流-热-固耦合一体化计算方法逐步应用于航天工程[1]。数值计算基本采用高精度CFD技术求解N-S方程与固体求解器相耦合的方式开展流-热-结构耦合研究[2-3]，对高超声速飞行器进行建模与分析仿真工作，并与对应的高超声速风洞试验的气动力、气动热和热响应测试数据进行对比与验证。但耦合计算中固体热传导和结构变形的求解大多是采用有限元[4-6]和有限差分技术[7]，而非效率更高的边界元求解。当前对高超声速流动与固体之间的耦合换热问题已进行了大量研究，提出了多种耦合方法和策略[8-10]。

随着各国在临近空间和火星探测的太空竞赛，新一代高马赫数、长航时、高机动飞行器和火星再入探测器壁面将面临严重的催化效应[11-15]。研究表明飞行器关键部位防热材料表面的催化效应最高可带来近50%以上的气动热载荷[16]，使其成为非平衡气动热研究领域的热点。针对此问题，诸多学者[17-20]在高温气体非平衡效应和气动热环境的数值模拟与理论分析方面做了大量研究工作，通过设定材料为非催化、完全催化和有限催化特性，基于CFD方法分析类返回舱[21]和有翼飞行器[22]等材料表面催化对热防护系统和气动热的影响，特别是对催化特性发生变化时的热流载荷预测进行了解析与修正[23]。催化效应会对飞行器翼身结合处的激波与湍流边界层相互作用产生影响[24]，数值分析与试验结果的对比分析表明[25]，壁面催化特性、表面温度和马赫数等参数都对激波/边界层相互作用和气动热载荷有重要影响。其中，催化热的出现很大程度增大了激波/边界层相互作用分离区的下游气动热[26]。对于壁面催化不连续和壁面滑移条件下的气动加热问题也进行了研究，在壁面催化不连续的条件下，会导致壁面温度产生“跳跃”现象[27]，而壁面滑移对壁面温度的“跳跃”几乎没有任何影响[28]，数值计算结果表明温度“跳跃”现象会导致航天飞机表面产生大约150K的温度跳跃，与测量结果相比该计算结果偏低[29]。遗憾的是，对于考虑表面催化效应的流动/传热多场耦合分析，研究甚少，董维中等[30]针对C/C材料，考虑由氧化反应和催化反应引起的热化学烧蚀和热效应，建立了表面温度分布与气动热的耦合计算方法，实现了流场非平衡、表面的热辐射以及热防护层内部的热传导效应的部分耦合。但是，该研究尚未考虑具体的催化反应过程，缺少针对飞行器表面的物理化学计算模型和内部热响应计算模型，进而建立完善的非平衡流场/表面催化/热传导多场耦合模型与求解策略，分析材料表面催化效应对耦合传热过程的影响。

基于此，本文在高超声速非平衡流动求解器与结构热力多场耦合计算框架之上，建立超高速流动/催化反应/传热多场耦合分析模型，基于高频等离子风洞开展ZrB2-SiC超高温陶瓷防热材料表面催化特性的测试，对比简化原子复合催化模型和有限速率催化反应模型对气动热的影响，揭示非烧蚀防热材料表面催化效应对耦合传热的根本原因，进而大幅度提升多场耦合计算对热载荷预测的可靠性，有效避免非耦合计算给防热设计带来的过高估计。

1 考虑表面催化反应的耦合计算策略

在非平衡条件下，材料表面会发生氧分子和氮原子的催化复合反应(如表1所示)，定义防热材料表面催化复合反应程度的参数为催化复合系数(简称催化系数)γ，大多数情况下γ被拟合为温度的函数，在CFD模拟中作为催化边界条件使用。本文主要针对简化催化原子复合模型和有限速率表面反应模型表征表面催化效应对耦合传热过程的影响，并对2种模型的计算结果进行对比分析。其中相对于反应3和4，形成异相的NO的反应5通常在气动热模拟中不予考虑，因此在简化催化原子复合模型忽略异相的NO生成。然而，研究发现等离子体风洞中的试样附近有NO生成[31]，并且在与OREX再入飞行数据的匹配过程中也证明了NO生成的重要性[32]，因此在有限速率表面反应模型中考虑扩散至邻近表面原子与气相中原子复合反应(E-R机制)以及与另一吸附原子复合反应(L-H反应)，其中S0为吸附系数，γer为反应效率，E为反应放热量。在之前建立的超高速流动-传热耦合模型[33]的基础之上，将表面相互作用模型嵌入CFD中实现其表面反应建模能力，并与FEM程序相耦合，具体计算流程如图1所示。这里仅研究催化效应对耦合传热过程的影响。

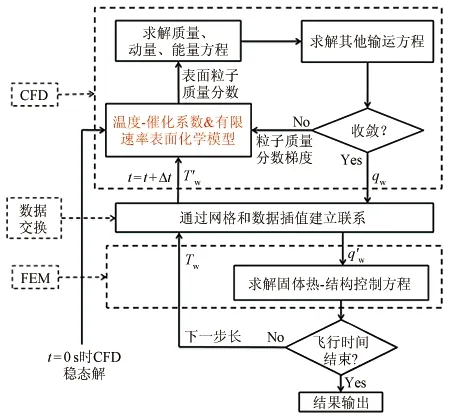
图1 考虑表面反应后的耦合策略

2 材料表面催化系数测试

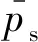
得到ZrB2-SiC材料表面催化系数随温度的变化如图3所示，可拟合为与材料表面温度相关的函数：

γ=1/[-109.61858+14114.02483(1000/T)6.45401]

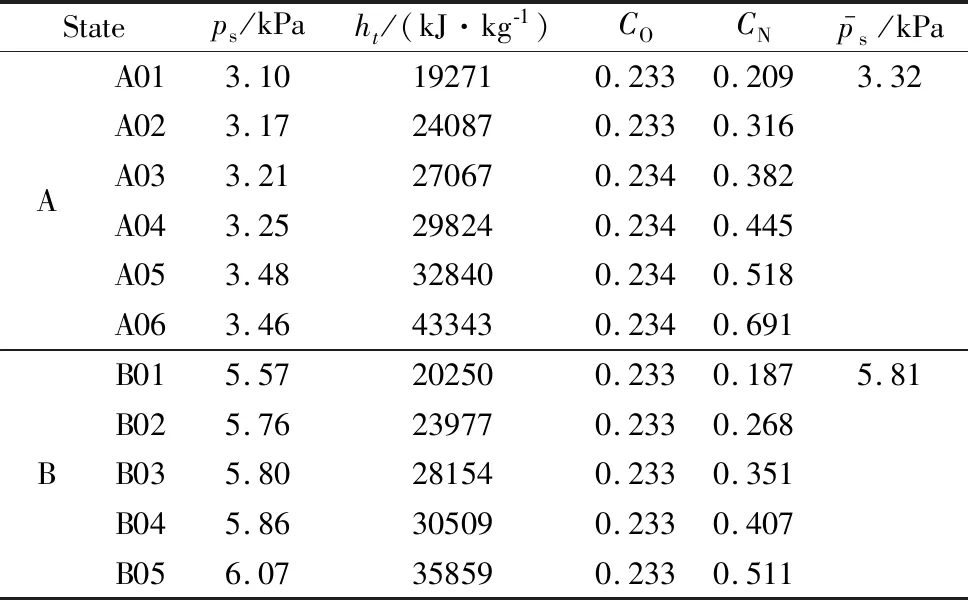
表2 高频等离子风洞流场参数Table 2 Wind tunnel parameters

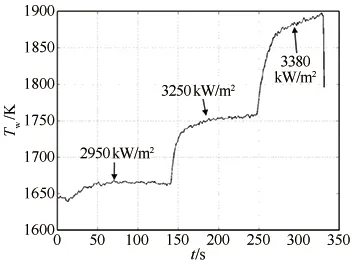
图2 不同试验状态下试样表面热流密度和温度历程

Fig.2Changecurveofsurfaceheatfluxandtemperaturewithincreasingtimeunderdifferentstates

图3 不同状态下试样表面催化系数

从试验结果可以看出，ZrB2-SiC材料表现出较低的催化系数且随着材料表面温度升高而逐渐增大，当表面温度低于1600K时，γ小于0.001且变化不大；而在更高的温度下，γ仍小于0.035。

3 考虑催化反应的多场耦合计算分析

3.1 耦合传热模型对热载荷的影响

针对ZrB2-SiC低催化非烧蚀防热材料，开展考虑表面催化效应的多场耦合计算，计算对象为轴对称头锥，几何尺寸如图4所示，自由来流马赫数、压力和温度分别为15、1090.2Pa和223.1K，飞行高度30.48km。不考虑气体辐射的影响，此时壁面处于气动加热、辐射散热、催化加热(完全催化)以及固体传热的热平衡机制，计算中假设氮原子和氧原子具有相同的壁面复合系数。首先对比催化和非催化壁面条件下非耦合的壁面辐射平衡和耦合传热对表面温度和热流分布的影响，如图5和6所示。

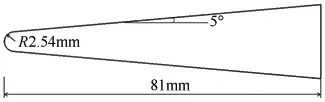
图4 几何模型

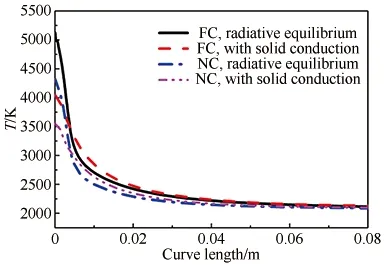
图5 有无固体热传导时的表面温度分布

Fig.5Comparisonofsurfacetemperaturedistributionswithandwithoutheatconduction

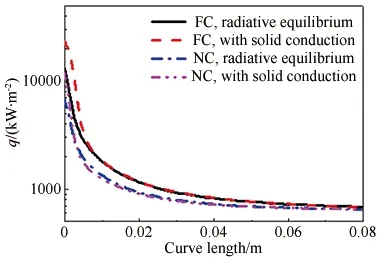
图6 有无固体热传导时的表面热流分布

Fig.6Comparisonofsurfaceheatfluxdistributionswithandwithoutheatconduction

从图5中可以看出，非耦合的辐射平衡假设结果高估了驻点温度并低估了锥面温度。这是由于超高温陶瓷材料具有较高的热导率，鼻锥处的一部分热载荷向内部快速进行热传导，而此热传导的存在降低了驻点温度并使后面锥面的温度升高。对于具有更高热导率的材料，这种效应会更明显。在非催化壁面条件下，考虑固体热传导时的驻点温度比辐射平衡假设结果低了780K，而在完全催化条件下则低了960K。

假定定常有限催化系数0.100～0.001，得到耦合传热下驻点压力、热流和温度如表3所示。结果表明壁面催化特性对壁面热流和温度有很大影响，而对压力没有影响。最低的非催化壁面热流与最高的完全催化热流相差了4.78MW/m2。

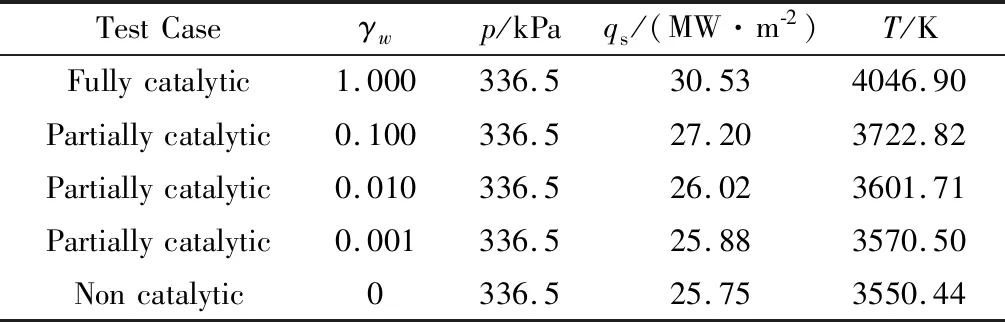
表3 耦合传热下驻点压力、热流和温度Table 3 Stagnation pressures, surface heat flux and temperature under coupling heat conduction

3.2 催化反应对气动热环境的影响

材料表面催化系数是壁面温度的函数，由于壁面附近原子发生复合，改变了壁面附近组分质量分数，因此气体混合物的热导率也发生了改变。类似的,可知模型表面不同时间、不同位置因温度不同其催化特性也有所不同。根据半经验Wilke公式[36]计算的热导率以及催化系数变化,得到材料表面催化系数(反应速率)与热导率、时间和表面位置的关系，如图7所示。图7(a)结果表明，随着壁面催化系数增大，混合气体的热导率略有增加。而催化反应速率随表面温

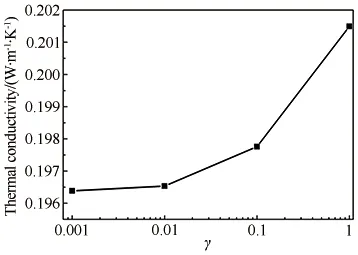
(a) 热导率与催化反应系数的关系

(b) 催化反应速率与时间的关系

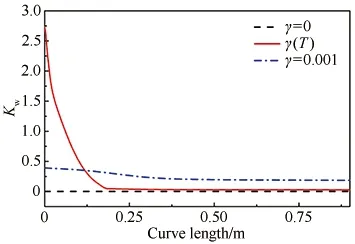
(c) 催化反应速率与表面位置的关系

Fig.7Thechangeofmaterialsurfacecatalyticpropertywiththermalconductivity,timeandsurfacelocation

度升高而逐渐增大。此外，由于催化系数是温度的函数，直接导致锥体表面不同部位的催化性能有所差异，用定常催化系数不能准确地对其进行表征，在后续的气动热环境计算中，上述物理量均非定值。

针对自由来流马赫数、压力和温度分别为9、574.6Pa和236.5K，飞行高度35km的飞行工况，分别采用简化原子复合催化模型和有限速率催化反应模型计算驻点热流随时间的变化，结果如图9所示。考虑固体结构内的瞬态传导过程，给出了2种化学反应模型计算的t=500s时刻的表面温度对比，如图10所示。由图可知，2种模型计算的结果基本一致，其中有限速率表面反应模型在驻点处温度稍低于简化反应模型，而在锥体后部温度则略高，二者的细微差别是由表面组分分布的不同所致。简化催化模型在对不同材料表面催化效应的初步研究中可以作为基准模型，更精细的研究则需要采用有限速率催化反应模型。

图8 几何模型和计算网格

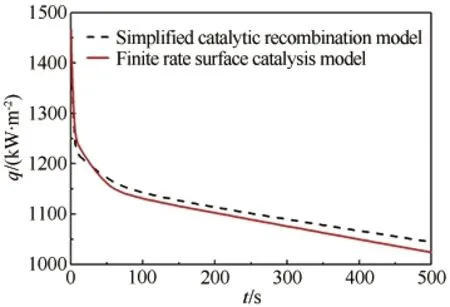
图9 驻点热流随时间变化

图10 t=500s时表面温度分布

3.3 催化反应对传热的影响

在上述耦合计算的基础之上，开展耦合传热过程中催化效应和壁面温度对换热系数影响规律的研究。耦合模型计算的有限催化和非催化壁面条件下的驻点处换热系数随时间变化的对比如图11所示。这里的换热系数定义为CH=q/(Tfilm,w-Tref)，表示物体表面与附近空气温差1K，单位时间单位面积上通过对流与附近空气交换的热量，单位为W/(m2·K)。Tfilm,w为流体边界层平均温度，Tref=226.91K。可以看出在整个耦合换热过程中，驻点处的换热系数整体上随时间变化呈上升趋势，尤其是在初始的短时间内变化较剧烈，而后逐渐趋缓，但是整体绝对值变化不大。另外由于催化效应的影响，有限催化壁面的换热系数整体上略高于非催化壁面的换热系数，表明催化效应的存在增强了周围气体的换热能力。

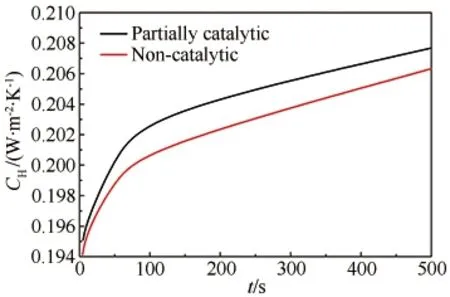
图11 驻点处换热系数随时间变化

Fig.11Theheattransfercoefficientofstagnationpointvaryingwithtime

将有限催化和非催化壁面条件下的驻点处换热系数随壁面温度的变化进行了对比，如图12所示。2种情况下的驻点换热系数均随壁面温度的升高呈现出近似线性增大的规律，且有限催化壁面的换热系数整体上略高于非催化壁面的换热系数。

图12 驻点处换热系数随温度变化曲线

Fig.12Theheattransfercoefficientofstagnationpointvaryingwithtemperature

4 结 论

(1) 建立了超高速流动/催化反应/传热多场耦合分析模型与计算策略，并通过高频等离子风洞获得了ZrB2-SiC超高温陶瓷材料催化系数与温度的函数关系。壁面的总热流取决于流动非平衡状态和材料表面催化特性，对于具有较高热导率材料的热响应，耦合传热分析能够有效避免非耦合计算带来的过度高估的结果。

(2) 材料表面气体热导率随着壁面催化系数的增大略有增加，从而使得飞行器表面的传热能力有所增加。简化催化模型在不同材料表面催化效应的初步研究中可以作为基准模型，更精细的研究则需要采用有限速率催化反应模型。

(3) 催化效应的存在增强了周围气体的换热能力，有限催化壁面周围气体的换热系数整体上略高于非催化壁面的换热系数，因此在传热分析中需要考虑表面催化效应以精确获得结构热响应。