重视矢量场定理在电磁场理论教学中的应用

李长胜 周 震 冯丽爽

(北京航空航天大学仪器科学光电工程学院，北京 100083)

“电磁场理论”或“电磁场与电磁波”是目前理工科电气、电子、通信以及光电信息科学与工程等专业本科生的重要基础课，理科物理专业本科生对应的类似课程为“电磁学”和“电动力学”。由于电磁场理论的抽象性，本课程普遍被认为是一门难教、难学的课程[1-3]。为了使学生学好这门课程，许多文献提出了各种有针对性的方法，以增强本课程的教学效果、降低教学难度。例如：(1)选择合适的教材和采用合理的教学方式[1]；(2)利用几何图形以及电磁场仿真图形和动画技术，采用形象化的教学方式帮助学生理解电磁场的概念和规律[4]；(3)加强实验课和实践课的教学环节[5]；(4)归纳总结电磁场的对称性和对偶性特点[6, 7]；(5)采用类比教学法，例如：将矢量场类比为流体中的流速场[8]；研究利用电磁力与惯性力的相似性[9]；(6)重视电磁场与电磁波的理论知识在各个领域中的应用，关注电磁学相关物理效应的教学，激发学生的学习兴趣[10]等。

矢量分析和场论是电磁场理论课程中的核心基础内容，有的工科院校将其单独开设为一门数学基础课程[11]，其主要内容包括标量场的梯度，矢量场的通量、环量、散度、旋度等基本概念，以及散度定理、斯托克斯定理和亥姆霍兹定理等基本矢量场定理。这些基本概念和定理提供了后续电磁场与电磁波课程内容的数学基础和“场”的基本思想，因而通常出现在相关教材的第一章[12-16]。

关于矢量分析和场论与本课程教学之间的关系，已有一些文献进行了相关分析和讨论，例如：文献[17]讨论了矢量分析在物理规律中的应用；文献[3]和[18]讨论了几何图形及矢量图分析在电磁场教学中的应用；文献[19]提出在电磁学教学中应强调“场”的物理思想和体系；文献[20]认为电场线的两大性质是静电场两大定理(即高斯定理和环路定理)的形象表述；等等。但目前尚未见有文献分析和讨论矢量分析和场论基础，特别是典型矢量场定理在电磁场理论课程教学中的重要作用。

本文在讨论场论基础知识与电磁场理论课程内容之间关联关系的基础上，提出在“电磁场理论”课程教学中应充分重视矢量场定理的普遍应用，从而可以帮助学生理解和掌握本课程内容，有效降低本课程的教学难度，提高教学效率。

1 场论基础与电磁场理论的关系

场是一种特殊的物质形态，是物理学中最基本、最重要的研究对象之一。“场”的概念和思想贯穿于物理科学发展的始终，在宏观、微观物理，尤其是近代物理中，均离不开“场”的思想，包括引力场、流体场、电磁场以及场的量子理论和规范场等[21]；场论既是物理学，也是数学的重要组成部分和研究对象[11]。场论基础知识提供了上述各种形态物理场的一般概念和基本规律，它描述了各种物理场均具有的共同属性，因此学好矢量分析和场论基础知识，正确理解和掌握“场”的一般概念、思想、规律及其数学表述，将有助于降低电磁场理论课程学习的难度，对于本课程教学具有重要指导意义。

电磁场是典型物理场之一，因而电磁场理论与场论之间是“特殊与一般”的关系。实际上，电磁场理论中的诸多概念和定理均是根据场论基础知识来定义和推导得出的，例如：利用标量梯度的概念描述电位与电场之间的关系；利用矢量场的散度和旋度描述电场、磁场与其场源之间的关系；利用散度定理和斯托克斯定理，可以将麦克斯韦方程的微分形式转换为积分形式，等等[12-16]。

因此在电磁场理论课程教学过程中，应充分重视矢量分析与场论基础知识的普遍应用，善于利用场论基础中的一般概念和定理分析、理解和掌握电磁场理论，以便降低本课程的教学难度，提高教学效率。

2 矢量场定理在电磁场理论中的应用

矢量场F的散度是为了描述F在空间某点M附近的通量特性而引入的，它定义为点M处单位体积内散发出来的矢量F的通量，即该点的通量源密度，其定义式为[12]

(1)

式中S为包围点M的任意闭合曲面，ΔV为S所限定的体积。

矢量场F的旋度是为了描述F在空间某点M附近的环流(量)特性而引入的，其大小等于该点处环流面密度的最大值，其方向是使环流面密度取得最大值的面元法线方向，其定义式为[12]

(2)

式中ΔS为经过点M的面元，C为ΔS的边界闭合路径，en为面元ΔS的正法线单位矢量。可见，点M处矢量场的旋度即是该点的漩涡源密度。

电磁场是一种典型的矢量场，矢量场的散度和旋度的概念始终贯穿于电磁场理论课程教学之中，例如：描述电磁场运动变化规律的麦克斯韦方程组是由电磁场量的两个旋度方程和两个散度方程组成的，因而可以利用电场、磁场的散度和旋度运算求解其场源；同时表明在无界、自由空间中的矢量场可以完全由其散度和旋度确定，这也是亥姆霍兹定理的核心内容。

矢量场的基本定理主要包括散度定理、斯托克斯定理和亥姆霍兹定理，这3个定理在电磁场理论中得到普遍应用；在教学过程中，要求学生深刻理解并熟练应用这些基本定理，将有利于学生顺利地理解和掌握电磁场理论中的有关概念、规律和分析方法，从而提高本课程的学习效率。

2.1 散度定理的应用实例

根据散度定理，矢量场F的散度·F在体积V内的体积分等于该矢量场在限定该体积的闭合面S上的面积分[12]，即

(3)

散度定理的典型应用实例主要包括：

(1) 静电场高斯定理与稳恒磁场磁通连续性[12]。可以利用散度定理将上述定理的微分形式转换为积分形式。在电通密度(或电位移)矢量为D的场域内任意取一闭合曲面S，S所包围的区域体积为V，S内的自由电荷体密度为ρv，已知静电场高斯定理(麦克斯韦第四方程)的微分形式为

·D=ρv

(4)

对式(4)两边取体积分，并利用散度定理即可得出静电场高斯定理的积分形式，即

(5)

式中Qv为体积V内的自由电荷总量。

稳恒磁场是有旋无散场，即对于磁通密度矢量为B的任意闭合曲面S内任意一点，有

·B=0

(6)

对式(6)两边取体积分并利用散度定理可得

(7)

上式即为稳恒磁场磁通连续性定理(麦克斯韦第三方程)的积分形式。

(2) 电流连续性方程与基尔霍夫电流定律[12,16]。利用散度定理，可以根据电流连续性方程的积分形式推导出其对应的微分形式。设某闭合面S所限定的体积V不随时间变化，且该区域内自由电荷体密度为ρv、传导电流体密度为Jc，则电流连续性方程的积分形式为

(8)

(9)

由于体积V是任意的，故根据式(9)可得出电流连续性方程的微分形式，即

(10)

此外，将式(5)代入式(8)等号右边，并利用散度定理可得，

(11)

式中Jd和Id分别为位移电流密度和位移电流。式(8)等号左边为流入和流出闭合面S的所有传导电流的总和，即

(12)

式中Ic为传导电流。将式(11)、(12)代入式(8)可得基尔霍夫电流定律，即

(13)

式中Ij为传导电流或位移电流。

(3) 坡印廷定理[12]。假设空间中闭合曲面S所限定空间场域V内的电场、磁场、电通密度、磁通密度矢量分别为E、H、D、B，电流密度矢量为J，则根据麦克斯韦方程组中的两个旋度方程，以及矢量恒等式·(E×H)=H·(×E)-E·(×H)可得，

(14)

式中w=(H·B+E·D)/2为电磁场的能量密度，对式(14)两边取体积分并利用散度定理可得坡印廷定理的积分形式，即

(15)

(4) 电磁场的动量守恒与转化定理[22]。假设介质中电磁场的动量密度矢量定义为

gem=D×B

(16)

动量流密度张量(或电磁应力张量)定义为

Jg=0.5(D·E+B·H)l-DE-BH

(17)

式中l为二阶单位张量，Jg为二阶对称张量，电磁场对自由电荷密度为ρ、恒定电流密度为j的静止带电系统的洛伦兹力密度为

f=ρE+j×E

(18)

则电磁场动量守恒与转化定理的微分形式为

(19)

对式(19)两边取体积分并利用散度定理可得该定理相应的积分形式为

(20)

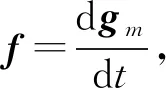
(21)

上式等号左边表示体积V内所有带电体的机械动量和电磁动量之和的时间变化率，等号右边表示该体积表面所受的总的面积力[23]。

(5) 电磁场的角动量守恒与转化定理[22]。假设电磁场的角动量密度矢量为

l=r×gem=r×(D×B)

(22)

式中,r为场点位置矢量，角动量流密度张量为

Jl=-Jg×r

(23)

则在各向同性介质中，电磁场的角动量守恒与转化定理的微分形式为

(24)

对式(24)两边取体积分并利用散度定理可得该定理相应的积分形式为

(25)

等号右边的体积分表示单位时间内场域V中总机械角动量(r×gm)的变化量。

2.2 斯托克斯定理的应用实例

根据斯托克斯定理，矢量场F的旋度F在曲面S上的面积分等于该矢量场在限定曲面S的闭合曲线C上的线积分[12]，即

(26)

斯托克斯定理的典型应用实例主要包括：

(1) 麦克斯韦第一、第二方程[12]。麦克斯韦第一方程(即安培环路定理)的微分形式为

(27)

对式(27)两边取面积分并利用斯托克斯定理可得对应的积分形式，即

(28)

麦克斯韦第二方程(即法拉第电磁感应定律)的微分形式为

(29)

对式(29)两边取面积分并利用斯托克斯定理可得对应的积分形式，即

(30)

(2) 磁通量的计算式[12]。根据磁通密度B与矢量磁位A之间的关系式B=×A和斯托克斯定理可得利用A计算磁通量Φ的公式，即

(31)

此外，根据式(30)、(31)和斯托克斯定理，可以推导出基尔霍夫电压定律[16]。

2.3 亥姆霍兹定理的应用实例

根据亥姆霍兹定理，若矢量场F在某闭合面S所限定的有限空间区域V内处处单值，且其导数连续、有界，场源分布在区域V内，则该矢量场由其散度、旋度及其边界条件唯一确定，且矢量场F(r)可表示为标量场u(r)的梯度的负值与另一矢量场A(r)的旋度之和[15]，即

F(r)=-u(r)+×A(r)

(32)

式中u(r)和A(r)的表达式分别为

式中r、r′分别为场点、源点的位置矢量。

亥姆霍兹定理的核心内容是自由空间矢量场完全由其散度和旋度确定，这可以用来诠释和理解为什么4个麦克斯韦方程组是关于电场强度和磁感应强度的散度和旋度的。许多文献分析讨论了亥姆霍兹定理在电磁场理论中的应用，例如：文献[24]从亥姆霍兹定理出发, 阐明了电位移与场源之间的内在联系。文献[25]讨论了该定理在电磁场理论中的贯穿作用，认为根据亥姆霍兹定理，可以由麦克斯韦方程组自然地引出标量电位和矢量磁位，并可方便地导出库仑定律或毕奥-萨伐尔定律，以及位函数与场在自由空间的积分表达式。

此外，文献[26]讨论了亥姆霍兹定理在求解静电场边值问题中的应用，可由亥姆霍兹定理直接导出静电场电位边值问题的一般积分解表达式，其推导过程简单明了。文献[27]从亥姆霍兹定理出发，合理导出静态与时变电磁场问题求解所需要的基本方程，并基于不同类型电磁场的特性给出对应的定解条件；由于静态和时变电磁场的不同特性，其所要求的边界条件有所减弱，即根据静电场的无旋性，其边界条件只需给定电场的法向分量，根据恒定磁场的无散性，其边界条件只需给定磁场的切向分量，对于时变电磁场，由于电场与磁场的相互耦合，边界条件只需给定电场或者磁场的切向分量。

3 结语

高斯定理是矢量场中闭合曲面积分与其所限定区域的体积分之间的一个变换关系；斯托克斯定理是矢量场中的闭合曲线积分与其所围曲面积分之间的一个变换关系；亥姆霍兹定理表明，一个矢量场所具有的性质可由其散度和旋度来描述，上述应用实例表明，这些矢量场定理普遍存在并始终贯穿于“电磁场理论”课程的诸多内容之中，因此在“电磁场理论”课程教学中应充分重视这些矢量分析与场论基础知识的广泛应用。

在多年的电磁场理论课程教学实践过程中，通过在绪论课及场论基础课中提醒学生重视上述矢量场定理的学习，并在后续课堂教学中提醒学生学会灵活运用上述场论基本概念、矢量场定理分析和理解电磁场理论，可以使学生更易于理解和掌握所学电磁场理论，做到融会贯通，从而可以有效降低本课程教学与学习的难度、提高教学效率。