数学核心素养视角下的解题探究
朱小扣


《普通高中数学课程标准(2017版)》中指出:“学科核心素养是育人价值的集中体现,是学生通过学科学习而逐步形成的正确价值观念、必备品格与关键能力,数学学科核心素养是数学课程目标的集中体现,是具有数学基本特征的思维品质、关键能力以及情感、态度及价值观的综合体现,是在数学学习和应用过程中逐步形成和发展的.数学学科核心素养包括:数学抽象,逻辑推理,数学建模,直观想象,运算能力,数据分析,这些核心素养既相对独立又相互交融,是一个有机的整体.”但是数学学科的核心素养怎么考?这是一个困扰广大数学工作者的问题.笔者将通过分析2018年以来各地的模拟考试试题,阐述六大核心素养的命题形式及解决方法.
一、数学抽象
数学抽象是数学的基本思想,是形成理性思维的重要基础,反映了数学的本质特征,贯穿在数学的产生、发展、应用的过程中.它反映了数学的本质特征,贯穿在数学的产生、发展、应用的过程中.数学抽象使得数学成为高度概括、表达准确、结论—般、有序多级的系统.
点评 本题通过建立直角坐标系,让学生能从情境中(即蜂巢结构图)抽象出数学的概念及方法,从而使得问题得到简化及解决.这样出题可以培养学生从具体到抽象的活动经验,有利于学生把握事物的本质,以简驭繁,运用数学抽象思维方式思考并解决问题.
二、逻辑推理
逻辑推理是指从一些事实和命题出发,依据规则推出其他命题的素养.主要包括两类:一类推理形式主要有归纳、类比;一类推理形式主要有演绎推理.
点评 上述两题通过数列的归纳、类比,实际上,就是从已有的知识和具体的事实经验出发,通过观察、实验、类比、联想、归纳、猜想等手段在某种情境和过程中推出可能性结论的推理.要做此类题时,一定要大胆猜想,这样就可以让学生学会有逻辑地思考问题;能够在比较复杂的情境中把握事物之间的关联,由简到繁,把握事物发展的脉络,从而能更好的认识事物的本质及变化规律.
三、数学建模
数学建模是对现实问题进行抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养.数学建模过程主要包括:在实际情境中,从数学的视角发现问题、提出问题、分析问题、建立模型、确定参数、计算求解,检验结果、改进模型,最终解决实际问题.
点评 通过构造距离型函数模型可以使得问题得到化归,迅速解决上述两个问题,使得学生理解数学建模的重要性.数学建模主要表现为:发现和提出问题,建立和求解模型,检验和完善模型,分析和解决问题.
四、直观想象
直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养.主要包括:借助空间形式认识事物的位置关系、形态变化与运动规律,利用图形描述、分析数学问题,建立形与数的联系,构建数学问题的直观模型,探索解决问题的思路.
例如学生掌握了三棱柱各个面延展分空间21个部分,正方体各个面延展分空间27个部分及其他棱柱的情形,那么三棱锥各个面延展可以把空间分成多少个部分?三棱台各个面延展可以把空间分成多少个部分?学生掌握和理解起来不容易,借助直观想象,笔者是按如下方法这样解释的.
例6 三棱锥各个面延展可以把空间分成多少个部分?三棱台各个面延展可以把空间分成多少个部分?
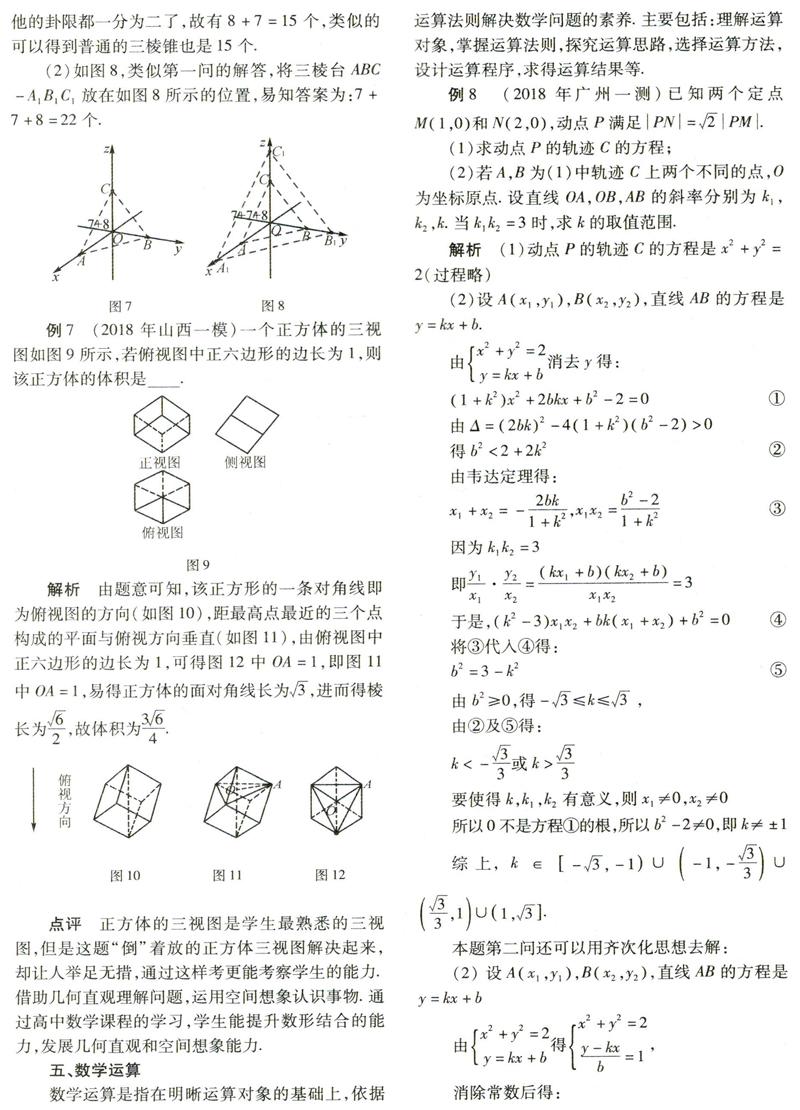
解析 (1)如图7,现将三棱锥O-ABC特殊成OA,OB,OC互相垂直,将其放在如图7所示的位置,8个卦限中,只有第七卦限没有被平面一分为二,其他的卦限都一分为二了,故有8+7=15个,类似的可以得到普通的三棱锥也是15个.
(2)如图8,类似第一问的解答,将三棱台ABC-A1B1C1放在如图8所示的位置,易知答案為:7+7+8=22个.
例7 (2018年山西一模)一个正方体的三视图如图9所示,若俯视图中正六边形的边长为1,则该正方体的体积是.
解析 由题意可知,该正方形的一条对角线即为俯视图的方向(如图10),距最高点最近的三个点构成的平面与俯视方向垂直(如图11),由俯视图中正六边形的边长为1,可得图12中OA=1,即图11中OA=1,易得正方体的面对角线长为3,进而得棱长为62,故体积为364.
点评 正方体的三视图是学生最熟悉的三视图,但是这题“倒”着放的正方体三视图解决起来,却让人举足无措,通过这样考更能考察学生的能力.借助几何直观理解问题,运用空间想象认识事物.通过高中数学课程的学习,学生能提升数形结合的能力,发展几何直观和空间想象能力.
五、数学运算
数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.主要包括:理解运算对象,掌握运算法则,探究运算思路,选择运算方法,设计运算程序,求得运算结果等.
点评 上述例题说明了在解析几何中,除了传统的方法外,还有齐次化方法,双根法,点差法,点乘法,极坐标等多种更简单的解法.类似地,在解决其他题目时,也可以一题多解,多种方法的融合可以进一步发展学生数学运算能力,有效借助运算方法解决实际问题.
六、数据分析
数据分析是指针对研究对象获取数据,运用数学方法对数据进行整理、分析和推断,形成关于研究对象知识的素养.数据分析过程主要包括:收集数据,整理数据,提取信息,构建模型,进行推断,获得结论.
例9 (巴蜀中学2018届高三1月考)统计显示,2011年之前,方便面销量在中国连续18年保持两位数增长,2013年的年销量更是创下462亿包的辉煌战绩;但2013年以来,方便面销量却连续3年下跌,只剩385亿包,具体如表1所示.相较于方便面,网络订餐成为大家更加青睐的消费选择.近年来,网络订餐市场规模的“井喷式”增长,也充分反映了人们消费方式的变化.
附题:
(2011年安徽省高考文科20题)某地最近十年粮食需求量逐年上升,表2是部分统计数据.
(Ⅰ)利用所给数据求年需求量与年份之间的回归直线方程y=bx+a;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该地2012年的粮食需求量.
点评 本题直接用时间代号比2011年安徽省文科高考第20题更简单,有时也会用Eaξ+b=aEξ+b,Daξ+b=a2Dξ等其他公式处理数据,也是为了引导学生找到最佳处理数据的方法,发展整理和处理数据能力.从而提升学生获取有价值信息并进行定量分析的意识和能力.
总结 林新建老师说过:“数学思想是数学素养的核心内容,唯有立意于思想,树立起运用思想引领解题的意识,才能真正培养和提升学生的数学核心素养.”为了发展学生的数学学科的核心素养,发展素质教育,培养德智体美全面发展的社会主义建设者和接班人,作为数学教育工作者的我,深感命题工作与教学工作的责任重大,但如何才能更好的发展核心素养呢?——“问渠哪得清如许?为有源头活水来.”实际上,只有从源头将核心素养融入命的题中,才能让学生在解题中理解和发展核心素养,我们不能让学生去证明一个假命题,也不能让学生去解一个无解的错题,只有反复斟酌,才能命出好题,希望本文对围绕核心素养命题的剖析,能帮助到大家.
(收稿日期:2018-11-12)

