基于组合模型的时栅信号处理系统健康状况预测*
杨继森,李路建,邵争光,李 明,牟智铭
(重庆理工大学机械检测技术与装备教育部工程研究中心,重庆 400054)
时栅传感器是一种基于时空转换思想的新型高精度位移传感器,具有结构简单、测量精度高、环境适应性强等优点[1]。经过长时间应用,传感器制作材料及其驱动电路、信号处理电路等会逐渐老化,这些因素将会引入误差源,导致传感器测量精度降低[2-5]。目前,提高时栅测量精度、减小测量误差所采取的措施有两类:①改进传感器结构、设计高精度激励信号等;②构建误差补偿模型,采用误差修正法等[6-13]。文献[6-7]提出一种平面线圈阵列传感器结构,解决齿槽结构影响行波磁场均匀性的问题。结构优化后的传感器在240 mm量程内的测量精度提高到±1 μm。文献[8]采用电磁仿真分析法,从误差角度对传感器的齿宽、齿槽等结构进行优化设计。经优化,在整周范围内传感器测量精度可达到±2″。文献[9]设计了一种采用闭环控制结构的高精度激励信号源,其输出正弦信号幅值精度为0.01%,相位精度为0.1%,将纳米时栅原始精度从1.4 μm提高至0.9 μm。文献[10]提出一种基于DDS原理结合程控放大电路的高精度激励信号模块。采用该激励信号可基本消除系统误差,将传感器短周期测量误差从±65″减小到±16″。文献[11-13]则是通过分析时栅传感器各类误差的来源、特性,构建转台误差模型、贝叶斯误差模型、直驱式误差模型等,实现误差修正,减小测量误差。以上技术方案主要是从测量源头和测量后续两个角度研究提高时栅传感器测量精度的方法,而针对时栅传感器的测量过程,保证时栅传感器测量精度的研究则相对较少。时栅信号处理电路经过长时间应用,容易出现电路老化现象,导致电路性能下降、影响电路信号传输。激励信号的幅值、相位均会因此发生变化而产生相应的误差,误差经传递最终会影响传感器的测量精度。因此,如何保证信号处理系统健康平稳运行、避免激励信号在信号处理过程中发生变化是提高时栅测量精度的第三种措施。研究时栅传感器信号处理系统的健康预测问题,可提前获悉系统运行状态,尽早排除故障隐患、避免损失持续扩大,在最大程度上确保时栅传感器在进行位移测量时,时栅信号处理系统处于健康平稳状态。
时栅信号处理系统以模拟集成电路为主,具有非线性以及元件容差性等特点,电路模块发生故障时,流经系统的激励信号会包含非平稳以及时变信息。ELMAN神经网络常用于故障模式识别,能实现非线性映射,且具备良好的时变性捕捉能力、强大的优化计算和联想记忆功能等[14]。另外,时栅信号处理系统的性能变化和时间密切有关,某些器件特性的变化曲线已知但同时又含有一些未知因素变化,如应用环境的电磁变化等;有时系统投入使用时间短,历史数据少。灰色模型能够对既含有已知信息又含有未知信息、少量信息的系统进行中长期预测,具有所需样本小、样本无需规律性分布以及计算工作量小等优点[15]。
为了有效利用两种模型的优点,扬长避短,获得优于单个模型的预测结果,本文提出一种基于ELMAN神经网络和灰色模型组合预测的时栅信号处理系统健康状况预测方法,使预测结果能同时反映系统健康状态发展的稳定性和随机性。通过分析激励信号误差对测量精度的影响,确定预测模型参数。考虑建模效率、预测精度,在构建ELMAN神经网络模型和灰度模型的基础上构建组合预测模型,同时制定健康状况诊断标准。实验结果表明,该方法能够准确预测时栅信号处理系统各模块电路的健康状况,预测值与实测值误差较小且相关性高,满足准确预测时栅信号处理系统健康状况的要求。
1 激励信号误差与测量精度
圆型场式时栅位移传感器的结构如图1所示。工作时,传感器定子和转子线圈之间的空气间隙会形成一个匀速旋转磁场,该磁场将在动测头和定测头导线上感应出电信号。两路感应信号的频率、幅值相同而相位不同,相位差代表所处的空间位置差,反映被测单元转动的角位移。对相位差进行解算即可得到被测物体角位移[5,8]。对激励信号变化与两路感应信号的输出关系进行分析,为根据激励信号的变化提前预测时栅位移传感器信号处理系统的健康状况打下理论基础。

图1 圆型场式时栅结构图
当激励信号发生变化时(幅值、相位存在误差),两相感应绕组实际输出信号为:
(1)
式(1)中,Δks,Δkc是两相感应信号的幅值误差;Δθs、Δθc是两相感应信号的正交误差值;Δθωs、Δθωc是两相感应信号的相位误差。
正常情况下,两路感应信号Us、Uc作差得到的合成信号为:
Ue=Us-Uc=Ksin(θ-φ)sin(ωt)
(2)
激励信号的变化主要带来两个方面的误差:
①导致感应输出信号与实际信号产生幅值误差。式(1)中Δks≠Δkc,假设仅有幅值不等,有测量误差ek,那么可得φ=θ+ek。通过计算,省略掉二次以上的微量且将二阶微量用一阶微量替换,则能得到测量误差:ek=0.5(Δks-Δkc)sin(2θ)。
②导致感应输出信号与实际信号产生相位误差。假设只有相位误差Δθωs和Δθωc,则感应信号为:
(3)
展开式(3)得式(4):
(4)
式(4)中微量Δθωs≈0、Δθωc≈0,仅保留一阶微量并且忽略二次以上微量,将二阶微量用一阶微量替换,可得:
(5)
将式(5)代入式(2)得合成信号:
Ue=K[sin(φ-θ)sin(ωt)+Δθωccosθsinφcos(ωt)- Δθωssinθsinφcos(φt)]
(6)
假设Ue=0,则φ≠θ,将产生的误差记为eω,设φ=θ+eω,代入式子(6),且Ue≠θ。省略掉二次以上微量并且用一阶微量替换二阶微量,得到测量误差:
(7)
由上述分析知,时栅激励信号的幅值误差和相位误差会导致时栅传感器的感应信号产生误差项ek和eω,最终影响测量精度。
2 理论与方法
2.1 ELMAN神经网络
ELMAN神经网络是典型的动态回归网络,具有适应时变特性的能力,其模型结构如图2所示[14]。

图2 ELMAN神经网络模型
ELMAN神经网络输入层作为数据输入端,输出层进行线性加权,隐含层函数可为线性或非线性,而承接层具有反馈作用[14]。
该模型的空间非线性数学函数为:
y(k)=g(w3x(k))
(8)
x(k)=f(w1xc(k)+w2(u(k-1)))
(9)
xc(k)=x(k-1)
(10)

(11)
ELMAN神经网络模型的动态跟踪预测能力极强,但需以大量的历史数据为预测基础。因此,对一些工作时间较短的时栅信号处理系统而言,因无充足的历史数据,不能获得很好的预测结果。
2.2 灰色模型
灰色模型的基本原理是以时间序列为横坐标,用微分函数来表示整个数据曲线的函数模型。具体说来,以对系统的发展、变化进行分析为重点,在此基础上对未来某一时刻的特征参数进行预测[15-16]。
考虑模型原理、算法简洁性,本文采用G(1,1)模型进行信号预测。建立G(1,1)模型的主要步骤如下:
①把采样到的n个样本数据进行累计求和,得到新的数据列x(1)(t),t=1,2,…,n,即
(12)
②将第一步产生的新的数据序列构建一组微分方程,方程中的a和u由式子(12)求出。
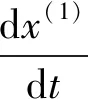
(13)
(14)
式中,B、X的具体表示如下:
(15)
(16)
其中BT是B的转置矩阵,(BTB)-1是矩阵BTB的逆矩阵,n是原始序列的个数。
③求解上述微分方程,得到一个关于时间的函数:
(17)
④求解式子(17)的原函数,得预测模型:
(18)
灰色模型中的G(1,1)模型能够实现参数预测功能,但在累加序列拟合时,离散解和累加序列之间会有误差存在,有时会对预测精度造成比较大的影响。
2.3 组合预测模型
基于上述两个模型的优缺点可知,单一模型可用于时栅信号处理系统健康状况预测,但由于样本数据需求、预测精度、计算效率等影响,在实际应用中存在一定局限性。ELMAN神经网络模型可用于预测工作时间较长、历史数据丰富的时栅信号处理系统,而灰色模型则更适用于历史数据少量的时栅信号处理系统。在充分考虑时栅信号处理系统各模块电路健康预测的实际需求的基础上,利用ELMAN神经网络模型的时变性捕捉、非线性映射能力结合G(1,1)模型对小样本、不确定规律数列具有较好预测效果这一特点,采用组合方式,基于加权-比例-平均思想,构建加权平方和平均组合预测模型,提高预测模型对样本数据量的适应性、扩大预测模型的适用范围及提高预测精度[16]。
(19)

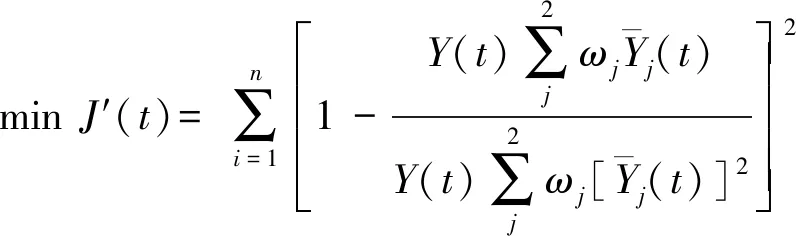
(20)
(21)
1≥ω1,ω2≥0
(22)
2.4 模型评价
模型建立之后,本文设计相对误差、预测均方差、相关系数3个评价指标对所建立的预测模型进行各项性能评估,检测模型有效性、可靠性。
(23)
(24)
(25)

2.5 健康状况预测
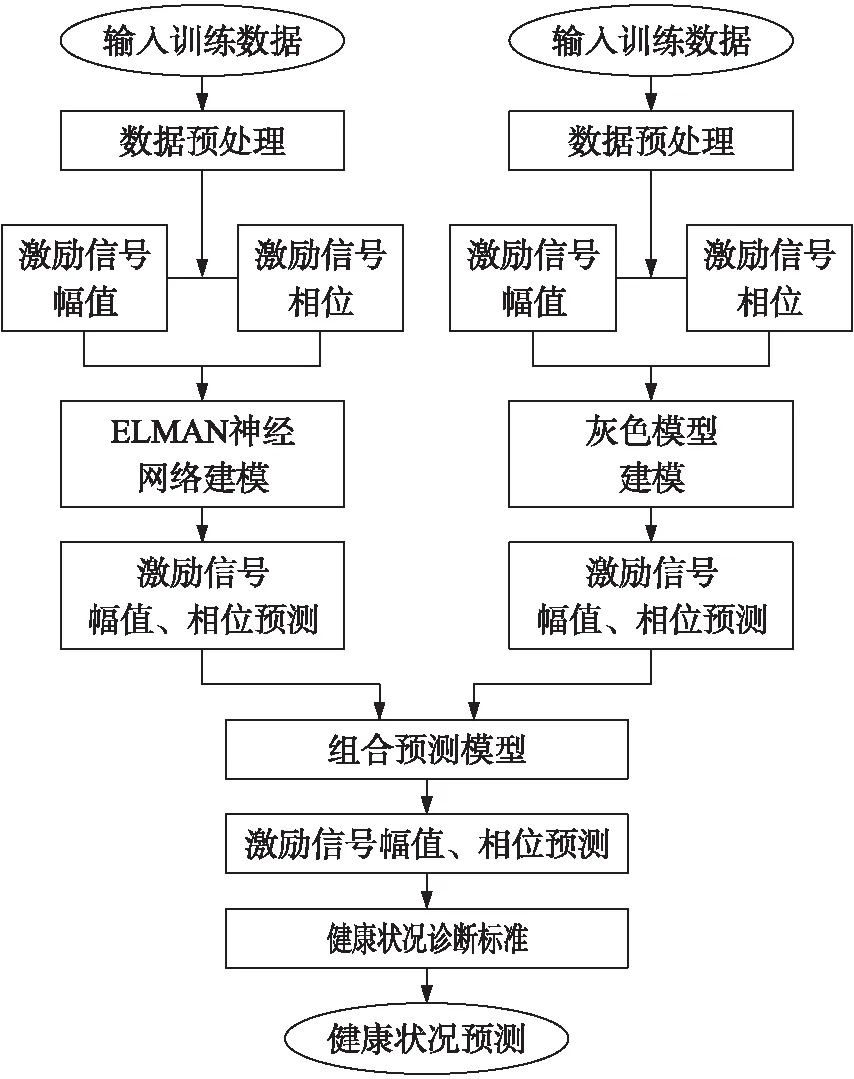
图3 健康状况预测流程图
3 模型建立
3.1 预测模型参数确定
由时栅传感器的测量原理分析可知,激励信号发生变化(幅值、相位发生变化),时栅的感应信号必将带有误差项,影响位移解算。对于时栅信号处理系统,模数转换、偏置电路、低通滤波、功率放大模块之中任何一个模块运行不稳或发生故障,激励信号都会发生幅值或相位上的变化,激励信号的状态可以直接反映时栅信号处理系统各模块电路的健康状态。由此,考虑以各模块电路输出激励信号的幅值、相位作为预测参数。预测参数的选取关系到健康状况预测结果的正确性、可靠性。本文采用克朗巴哈系数法对幅值、相位作为预测参数进行可靠性分析。
(26)

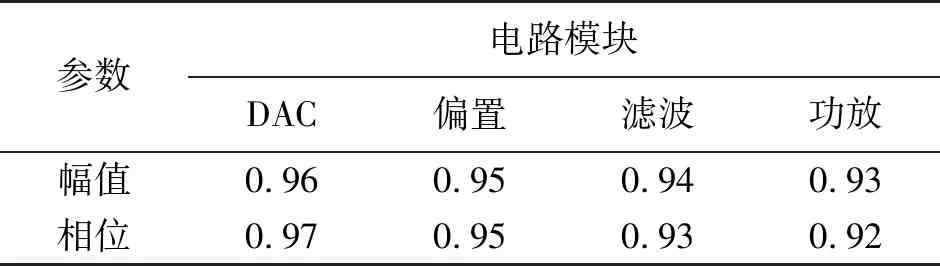
表1 参数可靠性系数

图4 时栅硬件平台与数据采集现场
表1中,幅值、相位的可靠性系数均达到0.9以上,说明所选参数可靠性高,选择合理。
3.2 预测模型建立
以圆型场式时栅传感器为例,以健康状态已知的时栅信号处理系统为实验对象,共设置4个数据采集端口,利用实验室搭建好的时栅传感器数据采集平台,每隔6 h连续采集DAC模块、偏置电路、滤波电路、功率放大模块的输出激励信号数据,实验平台如图4所示。考虑到现场采集数据时间过长,故以实验室数据库存储的该系统每隔6 h的历史数据为样本数据,导出每个电路模块各600个数据作为实验数据,其中,500个作为模型训练数据,100个作为模型检验数据,即以系统125 d的历史数据预测系统未来25 d内的健康状况。
ELMAN神经网络模型输入层、输出层各有2个结点,均为幅值、相位;参考ELMAN神经网络建模文献,采用公式法确定隐藏层结点个数,通过k=2×sqrt(m×n)+1确定[12]。此处m=2,n=2,计算得k=5,即隐藏层结点个数为5。模型结构为2-5-2,如图5所示。
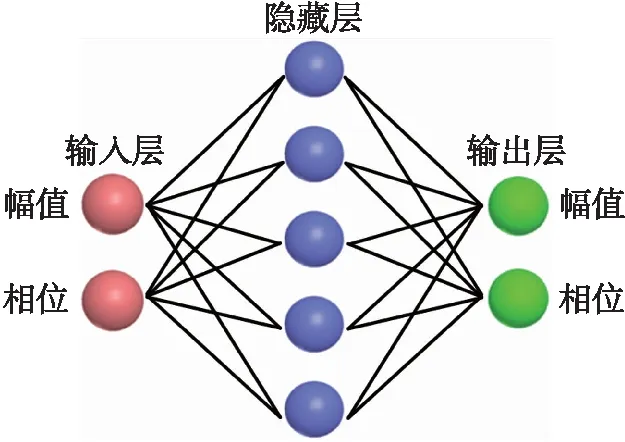
图5 ELMAN神经网络预测模型
按照G(1,1)模型建立步骤,构建幅值、相位参数预测模型,样本数据n=500。在ELMAN神经网络模型以及灰色预测模型构建完成的基础上,构建组合预测模型。根据ELMAN神经网络模型以及G(1,1)模型预测结果,代入二次规划模型计算ω1、ω2取值。
3.3 健康状况诊断标准
根据时栅信号处理系统运行实际,将其健康状态划分为三个等级:健康、亚健康、病态,分别对应于三种电路状态:①正常状态:电路对激励信号的影响很小,可忽略不计;②待检状态:激励信号幅值差、相位差已体现在感应信号中,需通过误差修正等措施才能保证传感器达到预期精度。技术人员可选择对电路进行检修,恢复正常状态;③故障状态:电路导致传感器出现不可修正的误差甚至错误。必须立即停止使用、需要进行维修。
若激励信号经过各模块电路后发生变化,幅值差、相位差的差值越大则表明电路健康状态越差。结合历年时栅传感器信号处理系统的运行状况及测量维修日志,考虑时栅误差补偿模型的效果,基于实验室现有的健康、亚健康、病态共三类时栅信号处理系统的测试数据构建健康状况诊断标准。将标准激励信号分别通入以上三类系统,采集激励信号在系统运行时,各模块电路输出激励信号的幅值及相位数据,以标准激励信号幅值和相位为真值,经系统运行后的激励信号幅值和相位为实测值,计算幅值差和相位差,确定健康诊断标准如表2所示。
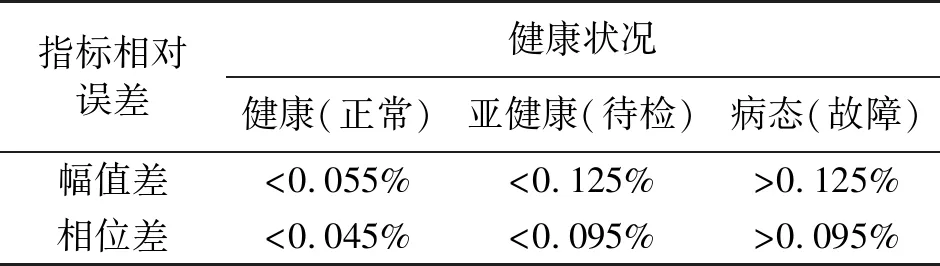
表2 健康状况诊断标准
该健康状况诊断标准的建立基于实验室现有的时栅信号处理系统,且仅适用于该类型时栅信号处理系统。若系统模块组成有所变化或者电路制作工艺有所改进,则需依据上述诊断标准构建过程重新计算和确定各指标的具体数据。
4 实验及讨论
将经过预处理的实验数据输入各预测模型,进行训练和测试。以功率放大模块输出激励信号的幅值预测为例,对实验结果进行说明。
由图6、图7可知,采用ELMAN神经网络模型、G(1,1)模型,所得的100个幅值预测值与实测值总体趋势一致,吻合度较高。经计算,两个模型的三个评价指标值如表3所示。模型相关系数R2均在98%以上,说明预测值与实测值吻合度高;相对误差值和预测均方差较小,说明预测误差较小。

图6 ELMAN神经网络预测结果(功率放大模块输出激励信号的幅值)
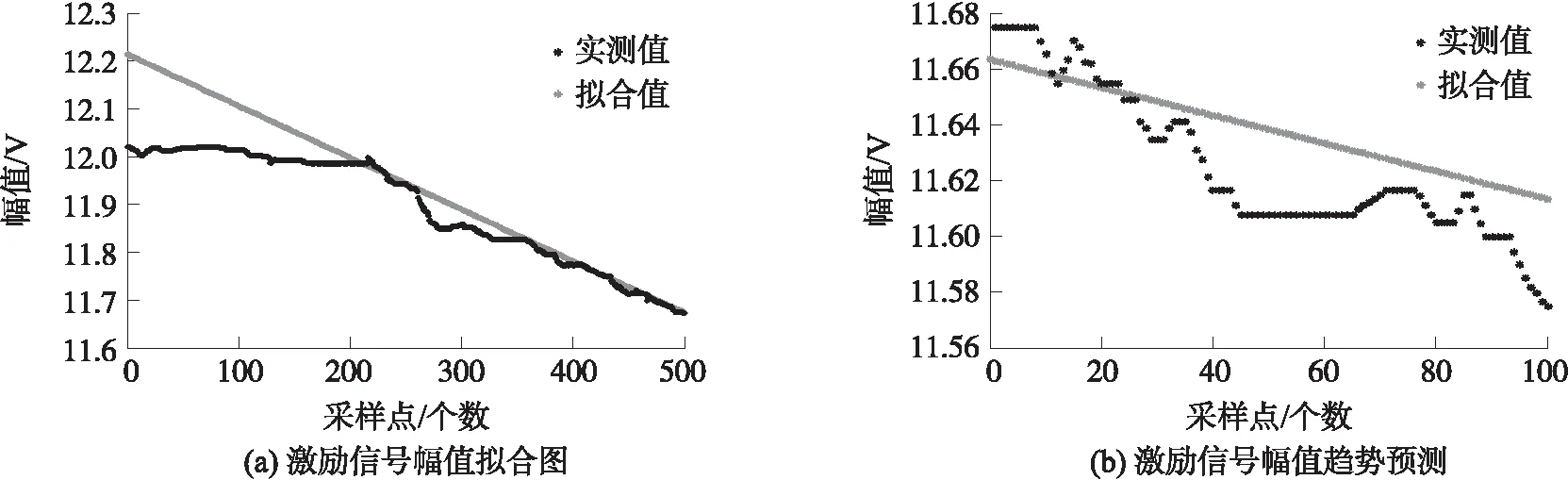
图7 灰色模型预测结果(功率放大模块输出激励信号的幅值)

电路模块预测模型ELMAN神经网络AVR2灰色模型AVR2组合预测模型AVR2DAC0.113 10.020 40.988 40.113 20.022 50.988 20.101 10.011 90.988 5偏置电路0.107 60.011 60.989 70.107 70.011 90.989 60.101 30.011 20.989 8滤波电路0.110 50.016 00.989 60.111 30.016 20.989 50.100 80.010 80.989 9功率放大0.112 10.011 80.988 50.113 70.012 10.987 10.101 60.010 60.988 8
注:A为相对误差;V为预测均方差;R2为相关系数。
对比两个模型的预测结果,前者的预测性能优于后者。结合二次规划模型计算出组合模型的ω1、ω2取值分别为0.7、0.3。
基于上述两个模型的预测结果,组合模型预测结果如图8所示。对比三个模型的幅值预测曲线图,组合模型绝大多数实测点离预测曲线都较近,且相关系数最高、相对误差和预测均方差最小,说明该模型预测性能最好、预测精度最高。各模型评价指标计算值如表3所示。
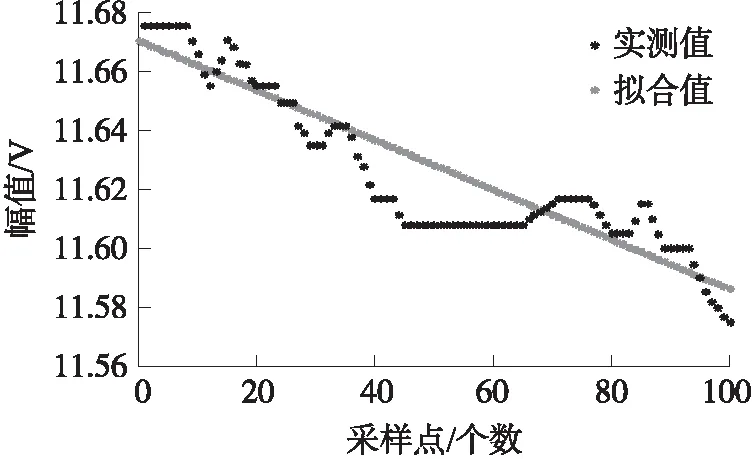
图8 组合模型预测结果 (功率放大模块输出激励信号的幅值)
分析组合模型预测结果,计算两参数相对误差值并与健康诊断标准作比较(见表2),健康预测结果如表4所示。
对比电路实际健康状况与模型诊断结果,ELMAN模型和G(1,1)模型都各有一个模块的诊断结果出现偏差,组合模型正确预测了四个模块的健康状况。采用组合模型比单一的ELMAN模型或G(1,1)模型,预测精度更高、健康状况预测效果更好。
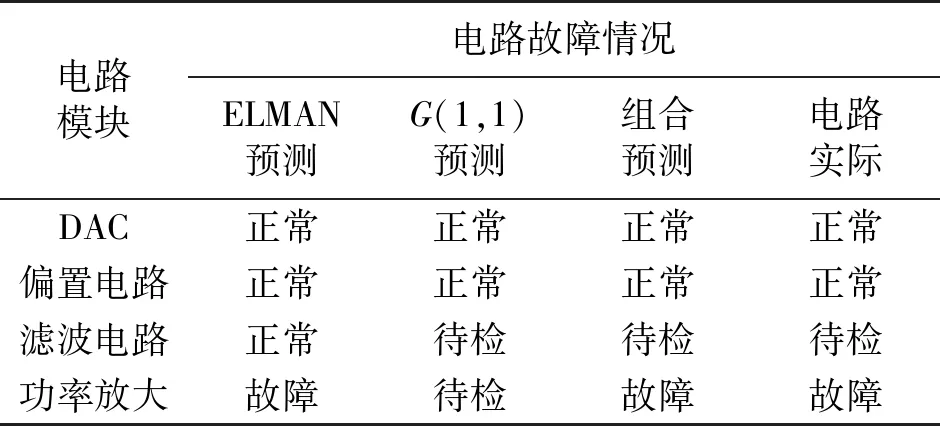
表4 模块电路健康预测结果
5 结论
时栅信号处理电路经过长时间应用,电路性能降低、稳定性下降、影响电路信号传输。与此同时,激励信号的幅值、相位均会因此发生变化而产生相应的误差,最终影响传感器的测量精度。针对此问题,本文提出一种基于ELMAN神经网络和灰色模型组合预测的时栅信号处理系统健康状况预测方法。通过分析激励信号误差对测量精度的影响,确定预测模型参数。在构建ELMAN神经网络模型和灰度模型的基础上构建组合预测模型、制定健康状况诊断标准。实验结果表明,该健康预测方法可靠性高、预测精度高,满足提前准确获悉电路系统健康状态的要求。对提高时栅位移传感器测量精度具有现实意义。

