应用逻辑方法解决杂合子随机交配并逐代淘汰隐性个体的问题
潘金元(安徽省望江中学 安徽安庆 246200)
在遗传学解题中,杂合子连续自交和连续自交并逐代淘汰隐性个体的问题讨论较多,师生非常熟悉,但对杂合子随机交配并逐代淘汰隐性个体的问题讨论较少,或者讨论、推理和计算的过程不严谨。笔者尝试应用逻辑方法计算其产生的Fn代的情况,特此交流。
1 逻辑方法简介
逻辑学是一门基础科学,是推理和思维的重要工具。本文运用的逻辑方法包括归纳推理、数学归纳法、演绎-推理。
由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理,称为归纳推理。简言之,是由部分到整体、由个别到一般的推理。归纳推理的结论是一种猜想,未必可靠,需要证明其正确性。
数学归纳法是一种特殊的证明方法,主要用于研究与正整数有关的数学问题。可按照以下2步进行:①证明当n 取第1 个值时命题成立;②假设n=k 时命题成立,证明当n=k+1 时命题也成立。完成这2 个步骤,就可断定命题对从第1 个值开始的所有正整数n 都成立。
演绎推理是从一般性的原理出发,推出某个特殊情况下的结论。简言之,是由一般到特殊的推理,与归纳推理相反。“三段论”是演绎推理的一般模式,包括:①大前提——已知的一般原理;②小前提——所研究的特殊情况(属于大前提);③结论——根据一般原理对特殊情况作出的判断。即集合M 具有某种性质P,m 是集合M 的子集,所以m 也具有性质P。在演绎推理中,只要前提和推理形式正确,结论必然正确[1]。
2 应用分析
例1,大豆是两性花植物,子叶颜色由一对等位基因控制,基因型BB 呈深绿、Bb 呈浅绿、bb 呈黄色(幼苗阶段死亡)。现有子叶浅绿大豆作为亲本随机交配,求成熟Fn的基因型类型及概率。
2.1 解法1:归纳推理和数学归纳法 先计算前几代成熟个体的基因型类型及概率(图1)。

图1 成熟个体基因型及概率计算图解
前几代成熟个体中基因型Bb 的概率分别是:P∶1Bb→F1∶2/3Bb→F2∶1/2Bb→F3∶2/5Bb→F4∶1/3Bb→F5∶2/7Bb,即P∶1Bb →F1∶2/3Bb →F2∶2/4Bb →F3∶2/5Bb→F4∶2/6Bb→F5∶2/7Bb。
观察规律,归纳推理,成熟Fn中Bb 的概率为,计算得出BB 的概率为。
下面利用数学归纳法证明该猜想。
假设当n=k 时,猜想成立,即成熟Fk为。
随机交配时配子结合如表1。
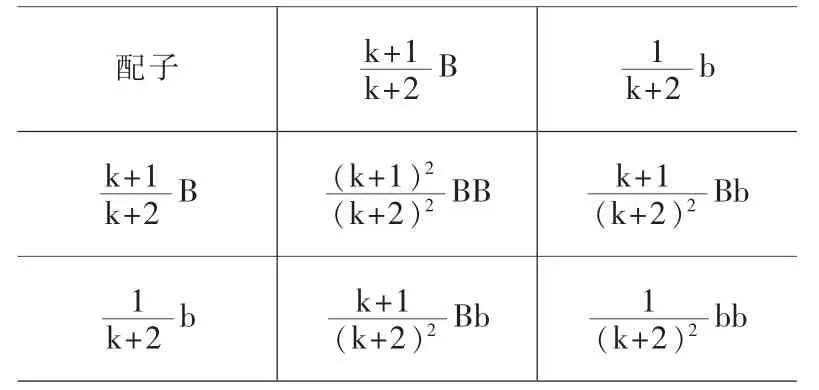
表1 成熟Fk 随机交配产生Fk+1
Fk+1为
bb 个体死亡后,成熟Fk+1为
所以,当n=k+1 时,猜想也成立。上述猜想得证。
2.2 解法2:演绎推理 假设成熟Fn中Bb 的基因型频率Pn(Bb)为x,则Pn(BB)=1-x,随机交配时配子结合如表2。

表2 成熟Fn 随机交配产生Fn+1
成熟Fn+1中淘汰bb 后,剩下BB 和Bb。其中。
将上式求倒数:

又很容易计算出成熟F1中Bb 的基因型频率,
根据等差数列的通项公式an=a1+(n-1)×d(其中a1为首项,d 为公差)可知,
上述推理过程运用的是演绎推理。如果一个数列的后一项与前一项的差值是常数,则该数列是等差数列,通项公式是an=a1+(n-1)×d,这是公认的原理,必然正确,是该演绎推理的大前提。,满足等差数列的特点,是小前提,且推理形式是正确的。所以,得到的结论一定正确。
3 结语
逻辑学是推理和思维的重要工具,加强逻辑思维能力的培养是现代素质教育的重要一环,是造就具有思维能力和创新潜力人才的有效途径。在《普通高中生物学课程标准(2017年版)》中,学科核心素养的“科学思维”素养就明确提出了“归纳与概括、演绎与推理等”。可见,让学生在学习过程中逐步发展科学思维,是新一轮课程改革所倡导的。

