贵州毕节白甫河人行索道桥力学性能分析

（中国葛洲坝集团第五工程有限公司，湖北 宜昌 443002）

索道桥是以钢丝绳或钢绞线为主要受力构件，钢横梁及木板等作为局部受力构件的一种柔性悬索体系桥梁［1］。因其投资少、架设快、施工简单及跨度大等优点，在西南山区应用较广，主要用来作为公路、铁路及水利等工程建设用的临时通道。

然而，索道桥是一种典型的柔性结构，荷载通过时变形大，几何非线性效应明显，目前我国并没有索道桥设计施工的规程规范［2］，现有文献对其研究也较少，而对其结构形式相似的悬索桥研究较多［3-4］。在为数不多研究索道桥方面的文献中［5-6］，大多都集中于车行索道桥研究，对宽跨比更小、结构更轻和几何非线性效应更明显的人行索道桥研究则更少。

本文以贵州省夹岩水利枢纽及黔西北供水工程北干渠3标临建设施中的白甫河人行索道桥设计施工为例，通过对索道桥索梁组合的几何非线性有限元分析，研究索道桥主索布置、横梁间距及抗风索张力结构参数对索道桥力学性能的影响，为索道桥设计和施工提供技术参考。

1 工程概况

白甫河索道桥是为便于白甫河跨河拱桥施工而修建的临时性桥梁。除方便两岸施工人员通行外，索道桥更重要的作用是在其上布设混凝土泵管，泵送混凝土至白甫河对岸。白甫河索道桥设计净跨径为200 m，全桥共布置8根主索，其中桥面索6根，两边各设置1根稳定索。主索均采用Φ40钢丝绳，绳股结构为6×19WS＋IWR，其标准强度为1 770 MPa。索道桥矢跨比为1/25，人行道净宽1.8 m，桥面索与稳定索采用Q235空心方钢横梁进行连接，索道桥设计荷载为2.75 kN/m。

本文以该桥为工程背景，通过建立索道桥索梁组合的空间有限元模型，分别研究索道桥主索布置宽度、横梁间距及抗风索张力结构参数对索道桥力学性能的影响，并以所得分析结果指导白甫河人行索道桥设计与施工。图1和图2分别为白甫河人行索道桥结构立面和横断面，主要由锚碇、承重索系统、连接调节构件、稳定结构和桥面系构件组成。

图1 白甫河索道桥结构立面（单位：mm）

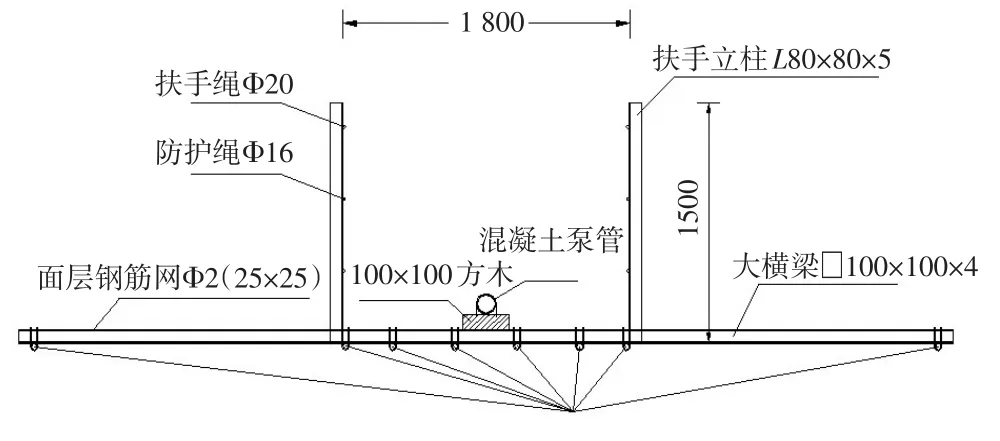
图2 白甫河索道桥结构横断面（单位：mm）

2 索道桥非线性有限元分析

2.1 有限元模型建立

索道桥主要是由柔性钢丝绳张拉而成，具有较强的几何非线性。根据索道桥结构特点，同时考虑索和梁的共同作用，采用LINK10杆单元模拟主索和抗风索，BEAM189梁单元模拟钢横梁，在数值有限元软件ANSYS中建立索道桥索梁结构有限元计算模型，由于桥面板和护栏不是主要受力构件，故未对其结构进行建模，仅将面板和护栏质量等效施加到主索中。LINK10杆单元使用只受拉选项时，如果单元受压，刚度将会消失，非常适合用于模拟主索的张紧或松弛。BEAM189梁单元可用于非线性大应变细长梁结构分析，且可使用SECTYPE、SECDATA、SECOFFSET定义任何梁截面形状。

索道桥的力学特性分析只有在确定其成桥状态后才能进行，由于索是柔性的，索上任意一点上的弯矩为零，可以推导出悬索的水平拉力H与悬索桥跨中最大垂度f之间的关系式为

式中，Mmax为简支梁的最大弯矩。

通过迭代法求得索道桥的成桥线形，具体实施过程如下：根据公式（1）可知，由索道桥成桥状态下的矢跨比可以求得主索的水平张力，迭代法的原理是在索曲弦线位置创建索道桥初始几何模型，采用索的实际材料性质和实常数，并设置很小的初应变，施加自重荷载及边界条件后在ANSYS中对索道桥进行几何非线性求解，逐步更新索道桥有限元模型，直到主索的水平张力与理论值近似相等即停止迭代，最后更新得到的有限元模型即为索道桥最后成桥状态。通过迭代法求得索道桥成桥状态有限元模型见图3，图4为索道桥局部放大图。该有限元模型共1 928个节点和1 924个单元。

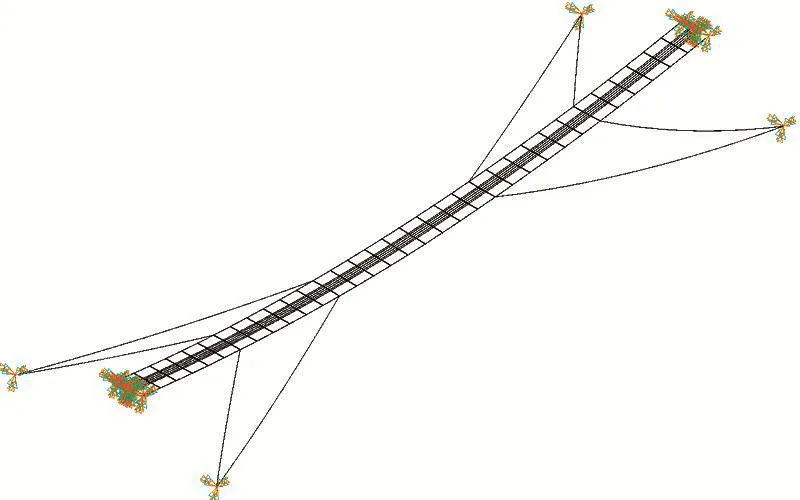
图3 索道桥有限元模型

图4 索道桥局部放大示意

2.2 计算边界条件

除自重之外，白甫河索道桥主要还受到其上的混凝土泵管、混凝土和人重以及外部风荷载作用。其值大小分别如下。

（1）由于混凝土泵管被固定在索道桥桥宽正中间，不考虑混凝土及混凝土泵管偏载影响，计算时荷载值取0.6 kN/m，均布设在索道桥中央。

（2）在桥宽1.8 m范围内，人群荷载都有可能发生，计算时考虑15人通行，且每人相距1 m处在索道桥最边缘，每人自重75 kg。

（3）根据JTG D60-2015《公路桥涵设计通用规范》［7］对风荷载计算规定，计算白甫河索道桥横桥向受到的风荷载为27.22 kN，均布设在索道桥桥跨范围内。

依据索道桥的实际受力情况，耦合钢横梁与主索搭接处平动自由度，主索与抗风索锚固端为完全固结，同时施加上述3种荷载条件进行索道桥力学特性研究分析。

3 结果分析

施加上述计算边界条件，逐步改变主索布置宽度、横梁间距及抗风索张力结构参数，对索道桥成桥状态下的有限元模型进行结构非线性静力计算，得到索道桥主索拉力、横倾角、横梁最大应力及最大位移力学参数，并将静力计算结果导入模态分析中，采用子空间迭代法进行索道桥大变形预应力模态计算，获得索道桥结构的自振频率。图5、图6分别为主索分布宽度和横梁间距为6 m、抗风索张力为10 kN时索道桥顺桥向正立面位移云图和索道桥一阶振型图。从位移图可以看出，索道桥在荷载作用下发生1.07 m位移，由于风荷载及人员的不平衡荷载，索道桥有一个横向倾角α，当横倾角过大时，会引起整个索道桥发生横向倾覆。从一阶振型图可以看出，索道桥振动频率较低，大小为0.317 0 Hz，且最易发生侧向振动。

图5 索道桥顺桥向正立面位移

图6 索道桥一阶振动

3.1 主索分布对索道桥力学性能影响

取索道桥上横梁间距为6m，抗风索张力为10kN，依次对主索分布宽度为5，6 m和7 m进行索道桥空间有限元模型分析计算，计算结果如表1所示。

表1 主索分布宽度对索道桥力学性能影响

从表1可以看出，主索分布宽度对索道桥主索拉力没有影响，对索道桥最大变形及一阶频率影响较小，对索道桥横倾角和横梁最大应力影响较大。主索分布越宽，索道桥横倾角越小，但横梁应力会逐渐增大。主索分布宽度由5 m增至7 m时，横倾角由4.45°减至2.71°，横梁最大应力却由70.01 MPa变大到92.5 MPa。因此在索道桥结构设计时,应适当增大索道桥主索分布宽度,以提高索道桥的抗倾覆性；但主索分布宽度过大时,会导致索道桥横梁结构尺寸变大，增大了索道桥结构自重。

3.2 横梁间距对索道桥力学性能影响

取索道桥主索分布宽度为6 m，抗风索张力为10 kN，依次对横梁间距为4，6 m和8 m进行索道桥空间有限元模型分析计算，计算结果如表2所示。

表2 横梁间距对索道桥力学性能影响

从表2可以看出，横梁间距对索道桥主索拉力没有影响，对索道桥最大变形及一阶频率影响较小，对索道桥横倾角和横梁最大应力影响较大。横梁间距越大，索道桥横倾角和横梁最大应力也就越大。横梁间距由4 m增至6 m时，横倾角由2.86°增到3.76°，横梁最大应力也由58.9 MPa变为120.3 MPa。如果横梁间距设置过小，会增加索道桥自重，不能充分发挥材料力学性能。在索道桥实际应用中，通过设置较大的钢横梁间距，在钢横梁间距之间再铺设密度较小木棱条作为小横梁，可提高索道桥横向稳定性及减小横梁应力。

3.3 抗风索张力对索道桥力学性能影响

取索道桥主索分布宽度为6 m，横梁间距为6 m，依次对抗风索张力为5，10 kN及15 kN进行索道桥空间有限元模型分析计算，计算结果如表3所示。

表3 抗风索张力对索道桥力学性能影响

从表3可以看出，抗风索张力对索道桥主索拉力、横梁最大应力及索道桥最大变形影响较小，对横倾角和一阶频率影响较明显。当抗风索张力由5 kN增到15 kN，横倾角由3.51°减小至3.34°，一阶频率由0.295 8 Hz增到0.325 4 Hz。抗风索张力增大，索道桥横倾角会减小，但减小幅度较小。抗风索张力增大会提高索道桥的一阶振频，增加索道桥结构刚度。

4 结论

本文采用几何非线性有限元法，建立了索道桥整桥有限元模型，在给定的计算边界条件下，分别从索道桥主索分布宽度、横梁间距及抗风索张力结构3个参数对索道桥力学性能的影响进行了分析，结果表明：

（1）主索分布宽度对索道桥主索拉力没有影响，对索道桥最大变形及一阶频率影响较小，对索道桥横倾角和横梁最大应力影响较大，主索分布越宽，索道桥抗倾覆性越好，横梁应力也会较大。

（2）横梁间距对索道桥主索拉力没有影响，对索道桥最大变形及一阶频率影响较小，对索道桥横倾角和横梁最大应力影响较大，横梁间距越小，索道桥抗倾覆性越好，横梁应力也较小。

（3）抗风索张力对索道桥主索拉力、横梁最大应力及索道桥最大变形影响较小，对横倾角和一阶频率影响较明显，抗风索张力越大，索道桥抗倾覆性越好，一阶振频也会随之提高。