《认识面积》教学

陈娟娟

【教学内容】

人教版五年级下册第五单元。

【教学过程】

一、两次观察体验活动，凸显“面”的二维性

1.第一次观察体验“面”——平面图形的面，线动成面，感知面的二维性与线的一维性的联系与区别。

（1）素材：课件演示“点动成线”的轨迹图。

问题1：如果一个点朝着一个方向移动，猜它的运动轨迹会形成什么？

生：线。

演示：课件展示两个涂着红色和蓝色颜料的点，朝着一个方向移动发现形成两条线段。课件演示两条线段对齐比长短，蓝色的线段比红色的线段长很多。

问题2：如果两个点一直不停地朝同一个方向移动，两条线的长度还能比较长短吗？

生：不能，因为线的长度范围无法确定，就不能比较长短了。

小结：在一定的长度范围里，线是有长短的，我们把线的长短叫长度。

（2）素材：课件演示“线动成面”的轨迹图。

问题1：如果一条线段朝着一个方向移动，猜它的运动轨迹会形成什么？

生：面。

演示：课件展示一短一长两条涂满红色颜料和蓝色颜料的线朝上面移动。

问题2：猜一猜，是短线移动形成的面大还是长线移动形成的面大？

生：长线移动形成的面大。

演示：形成一个红色的长方形和一个蓝色的长方形。课件演示两个长方形叠在一起比较大小，短线移动形成的红色长方形比长线移动形成的蓝色的长方形大很多。

问题3：为什么短线移动形成的面更大？

生：因为短线移动形成的面更宽更胖，面的大小除了看长度还要看宽度。

问题4：如果两条线段一直不停地朝这个方向移动，形成的面能比较大小吗？

生：不能，因为不能确定两个面的范围，所以不能比较大小。

小结：在一定的区域范围里，面是有大小的，数学里我们把面的大小称为面积。揭题：线有长短，线的长短用长度来表示，面有大小，面的大小除了看长度还要看宽度。面的大小用面积来表示，这节课就来“认识面积”。

2.第二次观察体验“面”——物体表面的面，面不离体，感知面的二维性与体的三维性的联系与区别。

（1）问题1：如果面朝一个方向移动，留下的运动轨迹会形成什么？

生：体。

演示：两个沾满颜料的长方形慢慢移动，形成两个长方体。

问题2：长方体上有面吗？在哪里？

生：有，在长方体的表面。

小结：面在体上，原来物体的表面也有面。

（2）素材：纸杯的侧面和底面，其他物体的表面。

问题：找一找纸杯的侧面在哪里？底面在哪里？

活动：用沾染颜料的手去摸出纸杯完整的侧面和底面，说说你有什么发现。

生：通过摸一摸、涂一涂发现侧面是弯弯的曲面，底面是平平的平面；面是一片片的，不像线是一条条的。

（3）问题：生活中还有哪些“面”？

活动：在教室里找一找“面”，并摸一摸。

生：橡皮的表面、数学书的封面、桌面、黑板面、门面、地面。

比较：桌面和黑板面谁更大？发现黑板面明显比桌面大。

小结：物体表面的面也有大小，物体表面的面的大小也叫面积。经过刚才的学习，我们知道了平面图形和各种物体表面的面有大小，数学里把面的大小叫面积。

举例：说一说什么叫面积？

生：黑板表面的大小就是黑板面的面积。课桌表面的大小就是课桌面的面积。

二、四次比较活动，建立“面积”的直观表象

1.第一次比较面积大小。

素材：一眼就能看出的大小不同的两张正方形纸片，两个大小比较接近但是用观察法和重叠法都比较不出来大小的正方形、长方形。

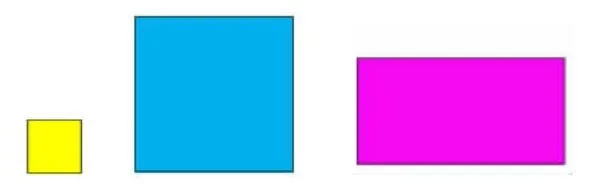
活动：比较三个图形的面积哪个最大，哪个最小？

生：观察法比较，第一个正方形最小，第二个和第三个通过观察比较不出大小。

生：通过把第二个和第三个图形叠一叠，把两个图形重叠的部分剪去，剪到最后，发现大正方形比大长方形正好多了1 个小正方形。

生：重叠法比较，通过重叠证明第一个正方形最小，虽然第二个和第三个无法通过彼此重叠比较大小，但是可以借助第一个小正方形估一估、量一量，发现大正方形里包含了9 个这样的小正方形，大长方形里包含了8 个这样的小正方形，9 大于8，所以大正方形的面积比大长方形的面积大。原来还可以用小的图形去测量大的图形的面积。

小结：观察法、重叠法可以帮我们判断面积的大概大小，用小图形去测量大图形的面积可以让我们借助具体数量比较面积大小。

2.第二次比较面积大小。

素材：小组合作用大小相同的圆形、等边三角形、正方形去量大正方形和大长方形的面积，比一比哪种图形更适合做面积单位。

记录单

思考：（1）正方形和长方形哪个面积更大？（2）比一比哪种图形更适合做面积单位？（3）观察活动记录，你有什么发现？

生：9＞8，15＞12，通过以上测量我们知道正方形面积大一点。圆形铺的面中间会有空隙，等边三角形铺的面边缘会有空隙，除非把等边三角形剪成两半才能铺完整的面，三种图形里只有正方形可以密铺。

生：圆形不适合作为面的度量单位，因为圆形不能密铺。虽然一个长方形用了8 个圆铺面，但长方形的面积一定比8 个圆形的面积大，因为用圆铺面的时候中间有空隙，这些空隙的面积还没被度量出来，所以圆不适合作为面的度量单位。

生：不能密铺的图形只要变成更小的单位也可以密铺。等边三角形虽然不可以密铺，但是铺在图形边缘部分的三角形剪成两半也能密铺，圆形不能密铺，要填完中间的空隙除非剪成无限细小的扇形，看来只要把图形变成更小的单位，也能完成测量。

生：图形不用铺完整的面，只要铺出一行一列就可以算出一共需要多少个面积单位铺面，行数乘列数正好等于面积单位的个数。

小结：正方形可以密铺，比等边三角形和圆形更适合做面积单位，当图形不能密铺时，可以通过剪一剪把图形变成形状更小能密铺的面积单位。

3.第三次比较面积大小。

素材：课件展示用小一点的方格量图形和大一点的方格量图形，引导学生发现测量单位还必须大小统一。

问题：长方形含有12 个正方形，正方形含有9 个正方形，难道长方形面积比正方形面积大吗？为什么？

生：测量单位大小不统一，不能比较大小。

小结：面积单位除了要满足“密铺”的条件外，还要满足“大小形状”标准统一的条件。

4.第四次比较面积大小。

问题1：同样是用小方格去量，同样用了3 个面积单位，为什么左边的图形面积更大？

问题2：为什么两个图形的形状不一样，面积却一样？

小结：几个面积单位不相交，面积就是相加；面积单位搬来搬去，面积是不变的。

5.通过四次比较面积大小，完成从形到数的转变，建立面积的表象。

小结：通过测量，我们把平面图形面积的大小比较变成面积单位个数的大小比较。其实面积，就是数一数、算一算有多少个相同的面积单位。

三、活动小结

师：什么是面？面在哪里？请举例。

师：什么是面积？请举例。

师：怎样的图形比较适合用来测量面积？