复杂背景下重叠椭圆形叶片的分割算法

刘鑫磊，梁 耀，黎双文，钟伟镇，李丰果

（华南师范大学物理与电信工程学院/广东省量子调控工程与材料重点实验室，广东 广州 510006）

【研究意义】随着农业生产的智能化和现代化，对植物生长状态和病虫害已逐步实现了实时监控，实时监控可为后期的管理提供依据。在植物生长状态和病虫害实时监控中，尤其是复杂背景或树叶相互重叠时，植物叶片图像的分割及其特征的提取是基础，也是当前研究的热点和难点。【前人研究进展】常见复杂背景图像中分割出目标对象的方法有边缘检测法（如Sobel算子等）［1-2］、阈值分割法（如大律法等）［3-5］和形态学分割［6-7］等。此外，孙俊等［8］提出一种基于改进 Otsu 算法的生菜叶片图像分割方法，该算法选取HSV颜色空间中的S分量，利用改进的粒子群优化算法搜索最优阈值，以该最优值作为Otsu算法的分割阈值，最终得到生菜叶片分割图；汪庆等［9］提出了一种基于归一化绿-红差异指数（NDI）颜色差异特征的叶片分割算法，能够将绿色叶片区域从自然环境中精确分割出来。为了提高复杂背景下目标树叶分割算法的运行效率和准确性，黎双文等［10］提出了一种超绿算法结合模糊C聚类算法分割树叶的方法；对于复杂背景下或光照不均匀的目标树叶，梁耀等［11］提出了一种基于GrabCut算法的复杂背景下或光照不均匀时目标树叶的自动分割算法。上述分割算法的目标对象是单片叶片，在对自然生长状态下目标叶片的实时监控时，监控图像中往往出现多片目标叶片或多片目标叶片重叠的情况，给目标叶片的分割和后期的特征提取带来极大困难。为解决这一问题，WANG等［12］提出了一种C-V模型结合改进Sobel算子的重叠叶片分割算法，该算法首先利用超绿算法去除背景中的非绿色部分，再分别以C-V模型和改进Sobel算子寻找重叠叶片的轮廓与边缘，将二者结合起来，从而分割出重叠叶片中的上片叶子。然而由于植物叶片的多样性和所获取图像的背景随机性和复杂性，难以找到一种普适的分割算法，因此需要对不同的目标叶片和不同背景下的分割算法进行深入研究。【本研究切入点】目前还没有研究一种普适的算法可以用于所有类型的叶片分割，因此本研究针对复杂背景下椭圆形重叠叶片的分割算法进行研究。【拟解决的关键问题】针对于自然生长状态下含有复杂背景的多片重叠的目标叶片，本研究提出一种提取特征点结合贪婪算法的分割方式，可以较为有效地分割椭圆形重叠叶片。该方法可为复杂背景下多片重叠目标叶片的分割提供算法参考，也为植物生长状态的实时监控算法奠定基础。

1 基本原理

1.1 超绿算法

由于植物叶片多为绿色，而背景中往往含有一些非绿色区域，如建筑物、地面和天空等，因此目标叶片与背景的RGB组成是不同的，绿色叶片的G分量要高于背景，所以可以用超绿算法［13-14］有效去除整幅图像中的非绿色背景。

设标记图像的像素为Si，G、B、R分别为需要分割图像的每个像素3个通道的像素值。超绿算法处理图像可以表示为：

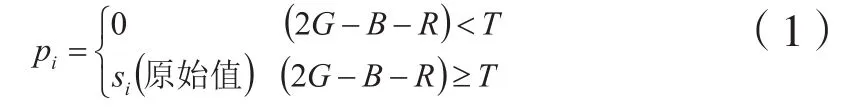
从式（1）可以看出，当需要分割图像的灰度化因子大于或等于阈值T时，对应位置的标记图像像素值不变；灰度化因子小于阈值 时，对应位置的标记图像像素值统一为0。

1.2 凹点检测和凸点检测

使用贪婪算法寻找上层叶片在重叠区域的边缘前，需将上层叶片的未重叠区域的边缘截取一部分并翻转到重叠区域作为贪婪算法的初始点，因此需先获得重叠叶片的尖端点和重叠部分的凹点。凹点用来确定截取边界，凸点用来确定对称轴。目前凹点检测方法有很多［15-18］，其中之一采用圆形模板来检测目标的凹点和凸点。本文采用计算圆形模板面积的方式来确定凹点与凸点。具体算法为，首先定义一半径为R的圆形模板，模板内的总像素点数为M。将该模板遍历重叠叶片的边缘点，将每个边缘点计算圆形模板内与重叠叶片区域相重叠的像素点的个数（图1圆圈中黑色部分的像素点个数即同时位于圆形模板与叶片区域的像素个数），设为A1；与非重叠叶片区域相重叠的像素点的个数（图1圆圈中白色部分的像素点个数即位于圆形模板内但不在叶片区域的像素个数），设为A2。

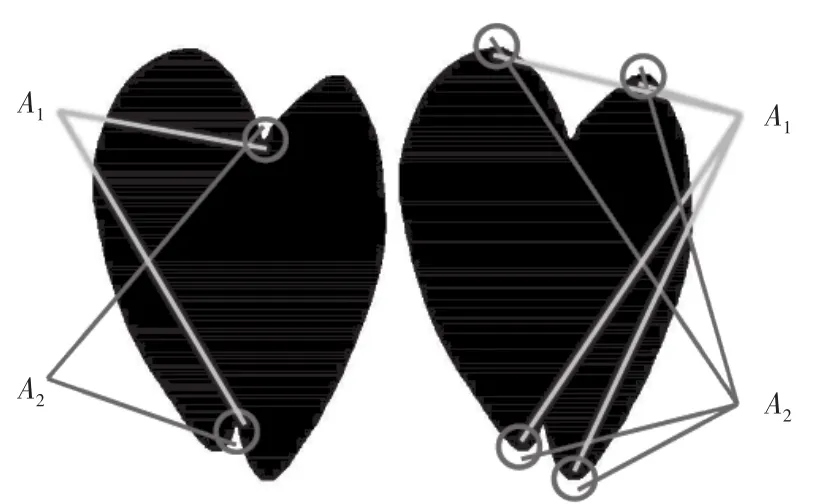
图1 凹点检测与凸点检测示意图Fig.1 Schematic diagram of pit detection and bump detection

根据式（2）判断第i个点Ci是否为凹点或者凸点：

式中，t1与t2分别为判断边缘点Ci是否为凹点或者凸点的阈值，二者不能相等。从式（2）可以看出，当模板内位于目标内（即A1）的点占比低于t1时，将该点判断为凹点；当模板内位于背景内的点（即A2）占比高于t2时，将该点判断为凸点。在凸点检测和凹点检测过程中，若有多个距离相近且满足式（2）的凸点和凹点，则它们的位置集中在图1中红圈区域。本算法中，每个位置只需要一个凹点或凸点，因此分别求得每一区域的中心点作为凹点或凸点检测的最终结果。

1.3 贪婪算法

重叠叶片分割的关键是准确获得上层叶片重叠部分的边缘信息。对于主叶脉左右完全对称的叶片，可先获得叶片的对称轴，然后将未重叠的边缘以对称轴为轴翻转即可得到重叠部分的边缘。但通常情况下，叶片并非完全左右对称，仅仅通过翻转并不能保证翻转后的边缘与上层叶片重叠部分的边缘完全吻合，需对边缘进行进一步处理。我们提出采用贪婪算法（又称贪心算法）［19-20］对翻转后的边缘进行处理，使得翻转后的边缘与上层叶片在重叠处的实际边缘吻合。贪婪算法是一种寻求局部最优解的算法，其基本思想是当需要处理多个问题的最优解时，可以取出其中一个问题并假定其他问题已经处于最优解，寻找此时该问题的最优解，当找到当前问题在当前情况下的最优解则以同样方法寻找下一问题的最优解，所有问题解决一遍则视为一次循环。

由于在重叠叶片的重叠区域中，位于上层的叶片边缘通常会比较清晰明显，因此，这一部分边缘的梯度会高于周围的叶面区域，所以本研究使用贪婪算法寻找梯度最大的边缘区域。由于所要寻找的边缘区域通常都是竖直方向上的，本研究所用贪婪算法的模板形状为1行n列的长方形，并以翻转得到的部分边缘作为贪婪算法的起始点，如图2所示。图2中的数值代表以Vi为中心的模板范围内与原图所对应的位置上的梯度值，Vi-1，Vi和Vi+1点为贪婪算法起始点中的连续3个点，其中Vi-1表示在本次循环中已经寻找过最大梯度值的点，Vi表示在本次循环中即将寻找最大梯度值的点，Vi+1表示在本次循环中下一个寻找最大梯度值的点。以图2中1行11列的模板为例，贪婪算法寻找最大梯度值过程为：在本次循环中，以初始位置的Vi为中心，建立一个1行11列的模板，将与原图对应的梯度数值放入其中，并比较整个模板中的梯度数值，选择其中梯度数值最大的位置，将该点在原图中的对应位置作为下次循环中新的Vi点位置（在整个过程中，不需要记录新的Vi点位置的具体梯度数值），以图2中模板内的梯度数值为例，则应将模板左数第2个位置在原图中对应的位置作为新的Vi点位置，当模板内存在多个相同最大梯度值时，则求出这几个最大值的中心位置在原图中所对应的位置，并将其作为新的Vi点位置，此时结束对点Vi的处理，对下一点即Vi+1点开始做同样的处理，直到本次循环结束（循环结束的标志为以上层叶片尖端点为轴翻转的边缘点全部以上述方式处理1次）。

图2 贪婪算法示意图Fig.2 Schematic diagram of greedy algorithm

1.4 凸包补缺算法

重叠叶片中上层叶片边缘的获取是对其准确分割的前提。在使用贪婪算法寻找上层叶片在重叠处的边缘点后，边缘点中存在不吻合的地方。个别边缘点偏离差到上层叶片的内部，这些偏离的点会导致上层叶片的分割出现缺口。因此需要用凸包补缺算法［21］进行补缺。凸包补缺算法的基本原理如下：

（1）确定凸包补缺算法的起始点并将所有排序。将所有点中纵坐标最小的点作为起始点，若存在多个纵坐标最小点，则选择其中横坐标最小的点作为起始点，以起始点为中心，建立坐标轴，依次计算其他点相对于起始点的幅角与距离，根据幅角大小进行排序，幅角相同则距离小的排在前面，如图3A所示。

（2）以起始点开始，取3个连续的点，判断中间点是否为凸包点。由起始点开始，依次取3个连续的点，如图3A所示，从P0开始，依次取3个点，即P0、P1、P2，依次连接3个点形成的形状称之为左旋，则此时可以确定P1为凸包上的点。

（3）根据第2步的结果确定新的起始点，并重复第2步。通过第2步确定点P1为凸包点，则以该点为新的起始点，依次取3个点，如图3B所示，从P1开始，依次取3个点：P1、P2、P3，依次连接3点形成的形状称之为右旋，则可以确定P2不是凸包上的点，此时需要继续以P1为起始点，跳过P2依次选择3个点，如图3C所示，连接的3个点为P1、P3、P4，可以判断这3个点所成的形状为左旋，则P3为凸包点，则以P3为新起始点。不断重复步骤二、步骤三，直到遍历所有的点，将所有凸包点按顺序连接起来，即可得到点集的凸包，如图3D所示，所得到的凸包即为点集的包络，点集内所有点都在点集的包络范围之内。

图3 凸包补缺算法示意图Fig.3 Schematic diagram of convex hull filling algorithm

2 算法流程

2.1 算法流程图

在算法中，需要设置的参数有凹点检测与凸点检测的模板大小。经过尝试，采取直径为410个像素的圆形模板，该模板可以使凹点检测与凸点检测效果最好。在使用贪婪算法时，使用的模板大小为1×201，该模板可以得到较好的移动效果。算法流程如图4所示。

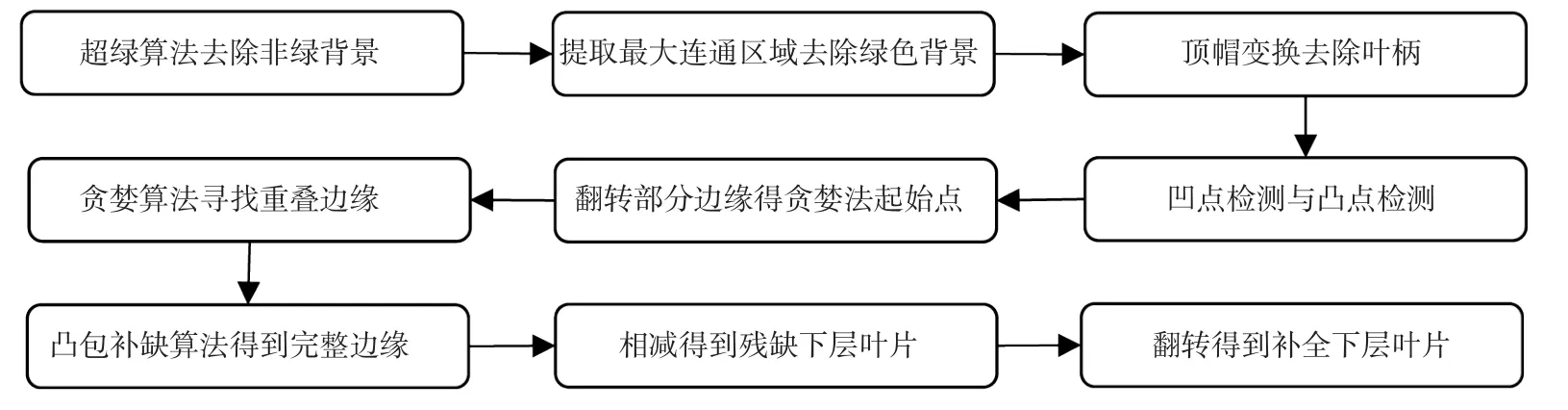
图4 复杂背景下重叠椭圆形叶片分割算法流程Fig.4 Flowchart of segmentation algorithm of overlapping elliptical leaves in complex background

2.2 算法流程描述

（1）利用超绿算法去除图像中的非绿色部分，如天空，大地，建筑物等；

（2）提取（1）中得到的图像中的最大连通区域，即重叠叶片区域；

（3）对（2）中得到的图像进行顶帽变换，去除叶柄；

（4）对（3）得到的图像进行凹点检测与凸点检测，得到叶片重叠区域的凹点以及尖端点；

（5）以目标叶片的两个尖端点所确定的直线作为对称轴，将与目标叶片重叠部分对应的外侧边缘点翻转至两片叶子重叠区域；

（6）以贪婪算法寻找目标叶片在重叠区域的边缘；

（7）对（6）得到的结果进行平滑，并与目标叶片的非重叠区域的点组合，得到完整的目标叶片边缘；

（8）对（7）得到的边缘进行凸包补缺处理并以此边缘分割原图像；

（9）用（3）得到的重叠叶片区域减去（8）得到的结果，得到下层叶片未被覆盖的区域；

（10）以（4）得到的下层叶片尖端点连线为轴，将下层叶片完整的一般翻转，得到下层叶片的补全图像。

3 结果与分析

3.1 目标树叶分割

（1）使用超绿算法去除非绿色背景。图5A为原图，图像中包含了大量非绿色背景，如建筑物、天空、大地等，因此首先通过超绿算法将这一部分非绿色的背景去除，得到图5B，可以看出该算法可以有效去除背景中的非绿色部分，但是对绿色部分无效。

图5 目标树叶的分割Fig.5 Segmentation of target leaves

（2）提取最大连通区域，去除绿色背景。在获取图像时，通常会以目标重叠叶片作为主体，因此重叠叶片在图像中所占绿色面积最大，提取图5B中的最大连通区域得到如图5C所示的重叠叶片区域，从而去除了绿色背景。

（3）顶帽变换去除叶柄。所得到的最大连通区域包含了重叠叶片与叶柄，而叶柄会导致凹点检测和凸点检测时出现偏差，因此需利用顶帽变换对图5C去除叶柄，结果如图5D所示。

（4）凸点检测与凹点检测。为了准确获得上层叶片在重叠区域的边缘，需要使用贪婪算法。为了不影响重叠叶片的其他边缘而只在叶片重叠区域使用贪婪算法，需要使用凸点检测与凹点检测算法分别得到两片叶片的尖端点和重叠区域的凹点，检测结果见图5E、F。

（5）将部分上层叶片翻转至重叠区域，作为贪婪算法的初始点。通过凹点检测与凸点检测得到的特征点将重叠叶片的部分边缘点翻转到重叠区域作为贪婪算法的初始点，具体做法为：通过上层叶片的两个尖端点可以确定一条直线L1，分别以两个重叠区域的凹点做一条垂直于L1的垂线L2和L3，将L2和L3之间的上层叶片外侧的边缘点以L1为轴翻转到另一侧，如图5G所示，以图5G可以看出，根据叶片的对称性，此时翻转得到的边缘点会位于上层叶片在重叠区域的边缘的附近，但仍然不是完全吻合。

图6 分割算法有效性验证Fig.6 Verification of the effectiveness of the segmentation algorithm

（6）使用贪婪算法准确得到上层叶片在重叠区域的边缘。为让翻转而来的边缘准确贴合到上层叶片的边缘，需使用贪婪算法来处理这一部分边缘点，由于在重叠区域内上层叶片的边缘是梯度最大的位置，因此使用贪婪算法使这一部分翻转得到的边缘点寻找到梯度最大区域即为目标叶片在重叠区域的边缘（图5H），将该边缘与上层叶片非重叠的边缘结合，得到图5I中完整的上层叶片边缘，以图5（I）中的完整边缘分割原图像，结果见图5J。

（7）使用凸包补缺算法对贪婪算法得到的结果进行补缺。从图5J可以看出，此时得到的边缘已经较为准确，但仍会存在个别边缘点存在偏差到了上层叶片的内部，从而导致该部分的上层叶片边缘存在缺口（图5J）。为解决这一问题，使用凸包补缺算法，该算法可以较为有效地填补边缘缺口，得到更为完整的上层叶片边缘。图5K为图5I经过凸包补缺算法得到的更为完整的上层叶片边缘，利用所得到的边缘对原图进行分割即可得到最终的目标叶片，如图5L所示。

（8）下层叶片残缺图和补全图。以整个重叠叶片区域减去上层叶片区域，得到图5M即下层叶片未被覆盖区域；下层叶片尖端点连线将其分为两部分，取完整的一半以该直线翻转，即可得到下层叶片的完整补全图像，如图5N所示。

3.2 分割算法有效性的验证

为检验分割算法的有效性，利用与样本1相同的算法和流程对其他样本进行分割，结果见图6。从图6可以看出，以PS抠图作为标准进行对比，有时不进行凸包运算即可得到较好的效果，如样本1中的图像，样本1中的图像中算法分割的结果没有明显缺陷，因此凸包对该结果影响不大。而样本2～5在未进行凸包时算法得到的结果有不同程度的缺陷，经过凸包算法后，缺陷得到弥补。

3.3 错分率分析

为了对分割准确率进行定量评价，选择人工在Photoshop软件中抠出的目标树叶作为评价标准，使用错分率来评价目标树叶分割的准确率。本研究将图像中的点定义为4种情况：算法分割的结果与手动分割的结果相比较，将分割正确的目标叶片上的点称为正确的目标（True Positive），将目标叶片上的点判断成了背景的点称为错误的目标（False Positive），将分割正确的背景上的点称为正确的背景（True Negative），将背景上的点判断成了目标叶片上的点称为错误的背景（False Negative），因此定义了相关的4种错分率计算方式。第1种是将背景误分割为目标的点即错误背景点占算法分割出来的目标点的比例，称为错误背景率（False Negative Rate，FNR）；第2种是将目标误分割为背景的点即错误目标点占算法分割出来的背景点的比例，称为错误目标率（False Positive Rate，FPR）；第3种为所有误分割的点占整个图像的比例，称为图像错分率（Error Rate，ER）；第4种为所有误分割的点占实际叶片的比例，称为叶片错分率（Error Rate for Object，ERO），具体计算公式为：

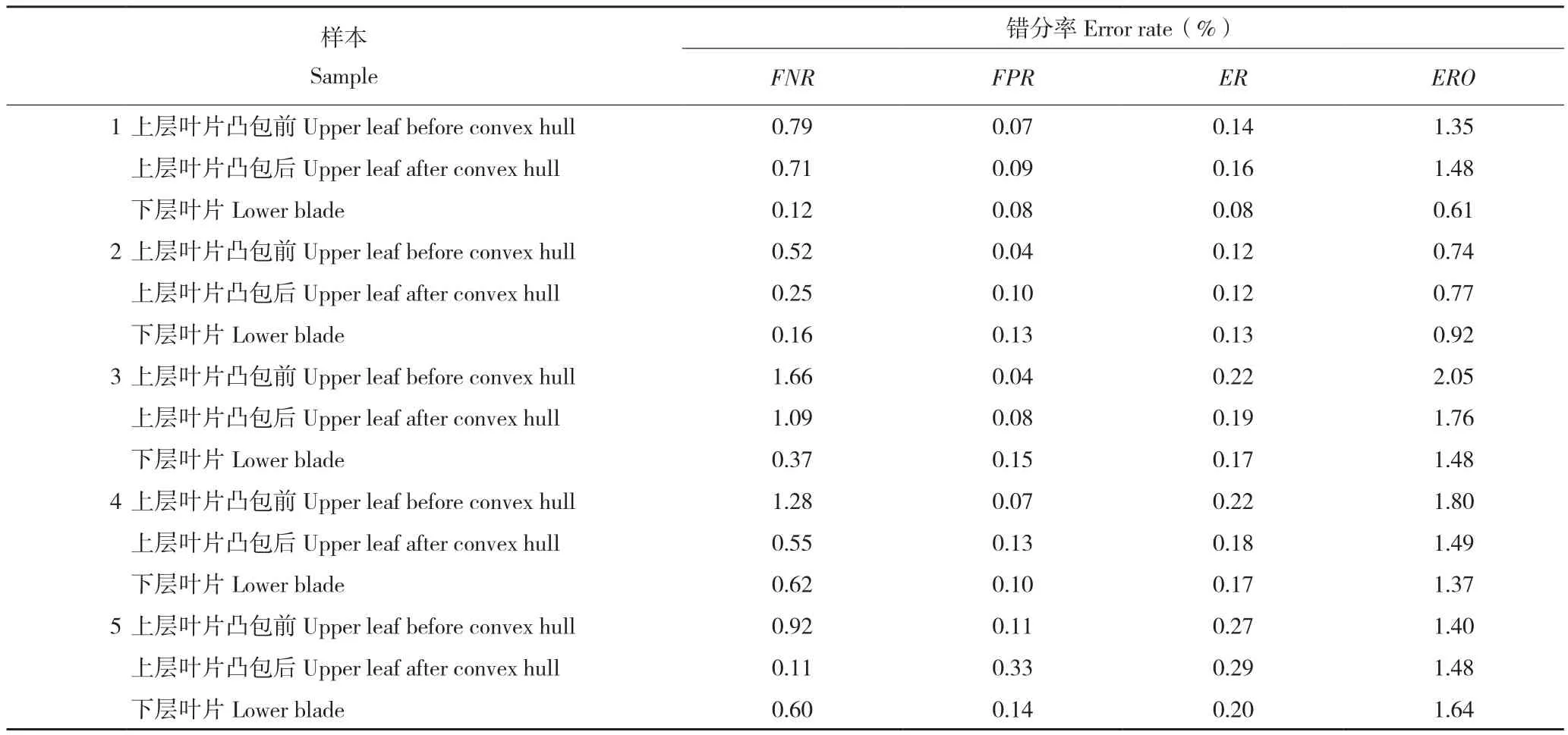
表1 样本错分率Table 1 Misclassification error of the samples

表1为计算得到的错分率。从表1可以看出，上层叶片与下层叶片的错分率均在3.0%以下，且大部分情况下经过凸包后错分率略有下降，也就是说分割准确率更高。

4 结论

为了实现在复杂背景下重叠椭圆形叶片的分割，采用了结合凸点检测和凹点检测的贪婪算法。通过与Photoshop软件人工抠图的对比，分析了所提出算法的错分率。结果表明，本算法在对复杂背景下重叠椭圆形叶片的分割有着较良好的效果，且错分率均在3.0%以下。这一研究可用于植物识别、生长状态及其病虫害的实时监控。然而算法在超绿这一步骤时，受光照影响较大，当叶片边缘部分光照明显不均匀时，会导致超绿后的叶片缺失，从而导致后续的凹点检测与凸点检测出现错误，影响算法的成功率；除此之外，本算法所涉及的叶片均是较为对称的，如不满足此条件，在使用贪婪算法时则难以得出理想结果，这些不足之处有待进一步研究改进。