基于主动学习Kriging的飞行器射程评估

王 浩,张海瑞,王 尧,洪东跑,何沛昊

(中国运载火箭技术研究院， 北京 100076)

随着武器装备的日益发展，临近空间高超声速飞行器具有高速度、强突防、强生存等优势，是世界主要军事大国的研究热点之一。与常规弹道导弹相比，新型高超声速飞行器具有大空域，宽速域的特点，其飞行环境更为恶劣、约束条件更为严格、不确定性影响更为显著。通用航空飞行器(Common Aero Vehicle， CAV)是一种机动灵活性极高的临近空间高超声速飞行器，具有典型的代表意义，CAV飞行器既可以从空间平台投放，也可以利用固体火箭发动机作为助推级从地面发射，具有良好的通用性和适应性[1]。

常规射程评估方法通过偏差组合考虑最大射程的最小值，以此包络预定射程[2]，由于忽略了系统固有的可变性以及模型的不确定性，在新型高超声速飞行器射程评估中具有一定的局限性和主观性，评估精度较差，同时难以实现射程裕度的量化分析。

针对新型高超声速飞行器的特点，综合考虑不确定性因素影响，开展飞行器射程概率评估具有重要意义，不仅可以作为衡量射程能力的重要指标，还可以为射程裕度分析提供定量依据。

在工程应用中，通常采用Monte Carlo方法对射程进行评估。Monte Carlo方法具有非侵入性和无偏性[3]，适用于求解隐式非线性问题，在工程中有着广泛的应用。然而，Monte Carlo方法需要调用大量的仿真计算模型，从而消耗巨大的时间成本和计算资源。为了进一步提升计算效率，近年来国内外学者结合代理模型和Monte Carlo方法开展了较多的研究工作。文献[5]结合Kriging模型的特点提出了主动学习Kriging方法，通过U函数序列加点，具有很高的计算效率。文献[6]进一步将主动学习Kriging和子集模拟方法相结合，提出了AK-SS方法处理小失效概率隐式非线性问题。

本文以某CAV构型为研究对象，利用固体火箭发动机助推发射，建立了气动、推进、质量、弹道学科分析模型，综合考虑不确定性因素影响，建立飞行器射程概率评估模型，通过引入主动学习方法和Kriging代理模型，对CAV构型飞行器射程进行概率评估。

1 飞行器射程评估建模

1.1 飞行器总体基准方案

以固体火箭发动机助推CAV构型飞行器方案为基准，假设飞行器从发射阵地点火起飞，经火箭发动机助推至一定高度后头体分离，进而，飞行器开始机动滑翔，依靠气动力控制实现跳跃滑翔，最后，在距离目标较近的时刻，实现弹道下压，进入末制导段，俯冲直至命中目标，确保飞行器的精确打击。任务剖面可划分为助推段、滑翔段以及末制导段,飞行器的任务剖面如图1所示[7]。

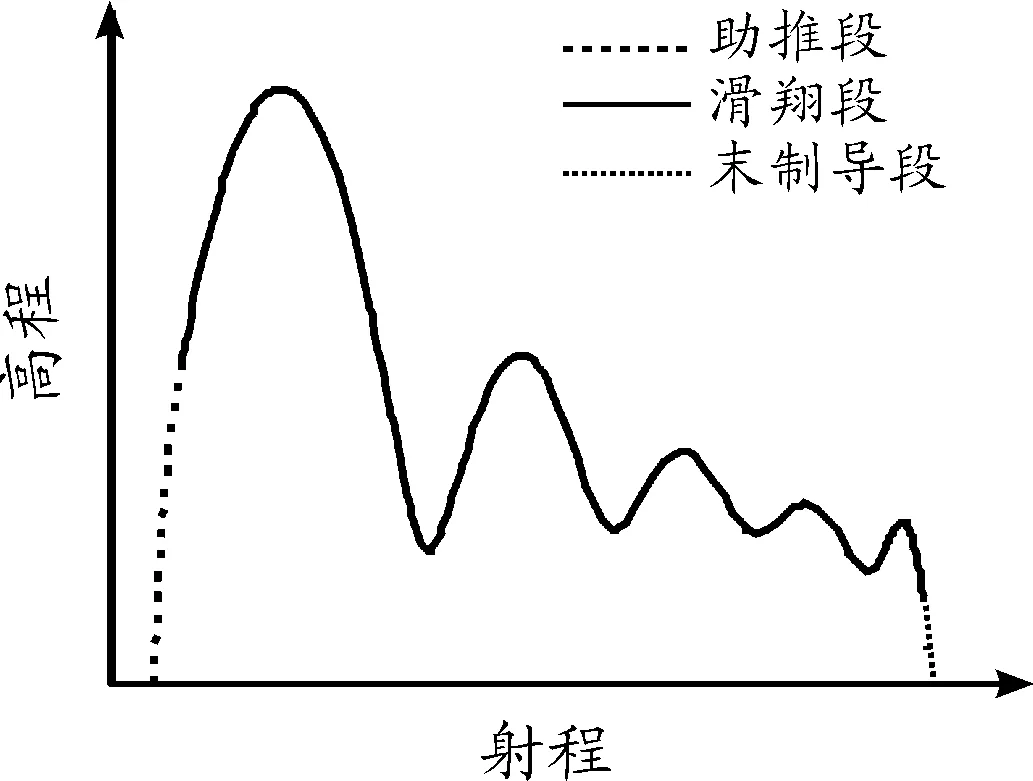
图1 新型临近空间飞行器任务剖面

由于末制导阶段射程与其他两段相比较小，只需要考虑助推段和滑翔段射程即可。此外，高超声速飞行器的射程与设计方案的气动、推进、质量、弹道4个学科密切相关，给出气动、推进、质量、弹道4个子学科与飞行器射程关系，射程仿真计算流程方块图如图2所示[8]。

1.2 学科分析模型

气动学科分析模型是根据飞行器总体基准方案的外形布局、气动学科设计变量以及飞行状态参数等计算气动力系数，包括阻力系数Cd和升力系数Cl。针对CAV构型滑翔弹头方案，采用文献[9]气动分析数据，结合总体方案滑翔高度及速度特点，选取典型滑翔高度为30 km，建立关于攻角α和飞行马赫数Ma的阻力系数和升力系数矩阵[10]，之后，通过线性插值计算某一攻角和马赫数条件下的气动力系数。

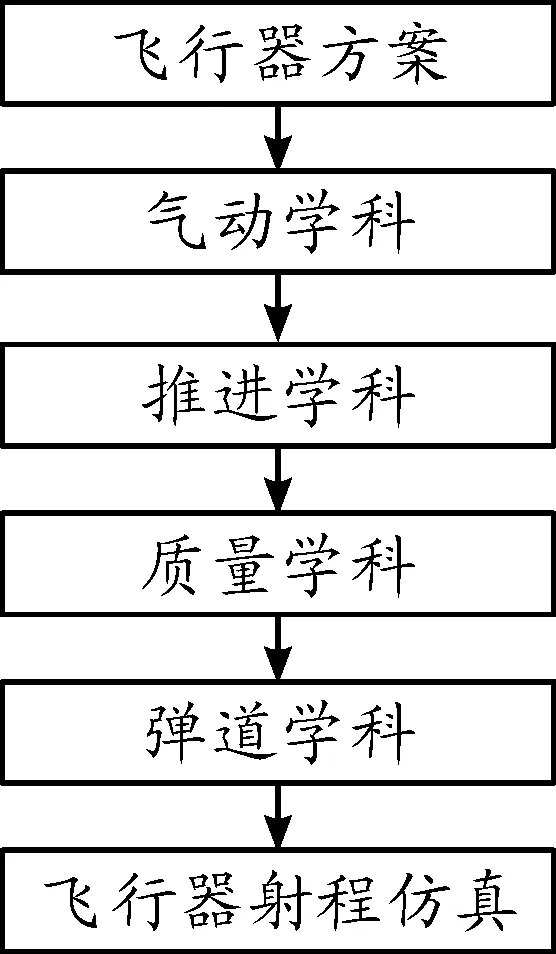
图2 射程仿真计算流程

推进学科分析模型是根据给定的发动机装药形式和装药参数，进行热力计算、内弹道性能计算、质量计算等，最终给出压强-时间曲线p(t)、推力-时间曲线T(t)以及秒耗量-时间曲线m(t)等。基于燃烧室内压力均一假设，推进学科分析采用零维内弹道计算方程组进行计算，具有计算速度快，计算精度适中的特点[11]。推进方案采用单室双推力固体火箭发动机，其药柱包括助推段和续航段两部分，从而在一定程度上弥补固体火箭发动机推力不可调节以及工作时间短的弱点。

质量学科分析模型主要包括CAV构型飞行器质量、发动机推进剂质量、发动机结构质量、以及尾翼、控制机构等结构质量。发动机推进剂质量可通过推进学科质量计算给出，发动机结构质量按照展开型质量方程计算[2]，包括筒体质量、前后封头质量、绝热层和包覆层质量、喷管质量以及点火器质量等结构质量。尾翼、控制机构等质量，在方案设计阶段可按相关成熟型号确定且保持不变。在发动机工作的助推阶段，飞行器质量随发动机推进剂的消耗逐渐减小；在无动力的滑翔阶段，忽略防热涂层的烧蚀作用，飞行器质量恒为CAV构型质量。

弹道学科分析模型是在其他学科分析结果的基础上，根据弹道运动方程实现飞行器自发射至末制导交接班的全过程飞行仿真。本文将弹道学科模型处理为轨迹优化问题，以飞行器射程最大为优化目标，在初始约束、终端约束以及控制约束等因素影响下，利用hp自适应伪谱法实现弹道优化[12]，在轨迹优化过程中，气动分析模型通过插值计算直接嵌入至弹道方程中。hp自适应伪谱法融合了Radau伪谱法与hp型有限元法的优势，在若干离散点上，通过多项式近似替代微分方程约束，从而将最优控制问题转化为非线性规划问题，具有很高的计算精度，其优势在于当某一离散区间的计算精度不满足要求时，可以自适应调整该区间内的配点数h和多项式阶次p，提高多项式近似的精度和效率。hp自适应伪谱法的计算流程如图3所示。

1.3 飞行器射程概率评估模型

针对新型高超声速飞行器大空域，宽速域的特点，在学科分析模型基础上，综合考虑气动、推进、质量学科的不确定性因素影响，将不确定性因素注入飞行器射程仿真模型。

假设飞行器飞行过程中的不确定性因素为X=[x1,x2,…,xn]T，给定目标射程为d0，则在不确定性干扰因素影响下，飞行器最大射程满足给定目标射程d0定义为可信射程D，即

D={d|d(X)-d0≥0}

(1)

式(1)中，d为某一不确定性因素条件下的最大射程。在不确定性因素影响下，飞行器最大射程在某一区间内呈现一定的概率分布，进而，可信射程出现的概率定义为射程的可信程度R，即射程概率评估模型为

R=Pr(d(X)-d0≥0)

(2)

针对这一模型，通过工程经验和相关成熟型号数据确定不确定性干扰因素的分布类型及其分布参数，进而通过Monte Carlo方法开展新型高超声速飞行器射程概率评估。然而在工程应用中，Monte Carlo方法需要调用大量的射程仿真模型，其中弹道学科模型为轨迹优化问题，导致射程概率评估效率较低。针对这一问题，提出了一种基于主动学习Kriging的飞行器射程概率评估方法，利用主动学习和Kriging模型特点，通过序列加点策略自适应更新Kriging模型，进而结合Monte Carlo方法高效开展射程概率评估。

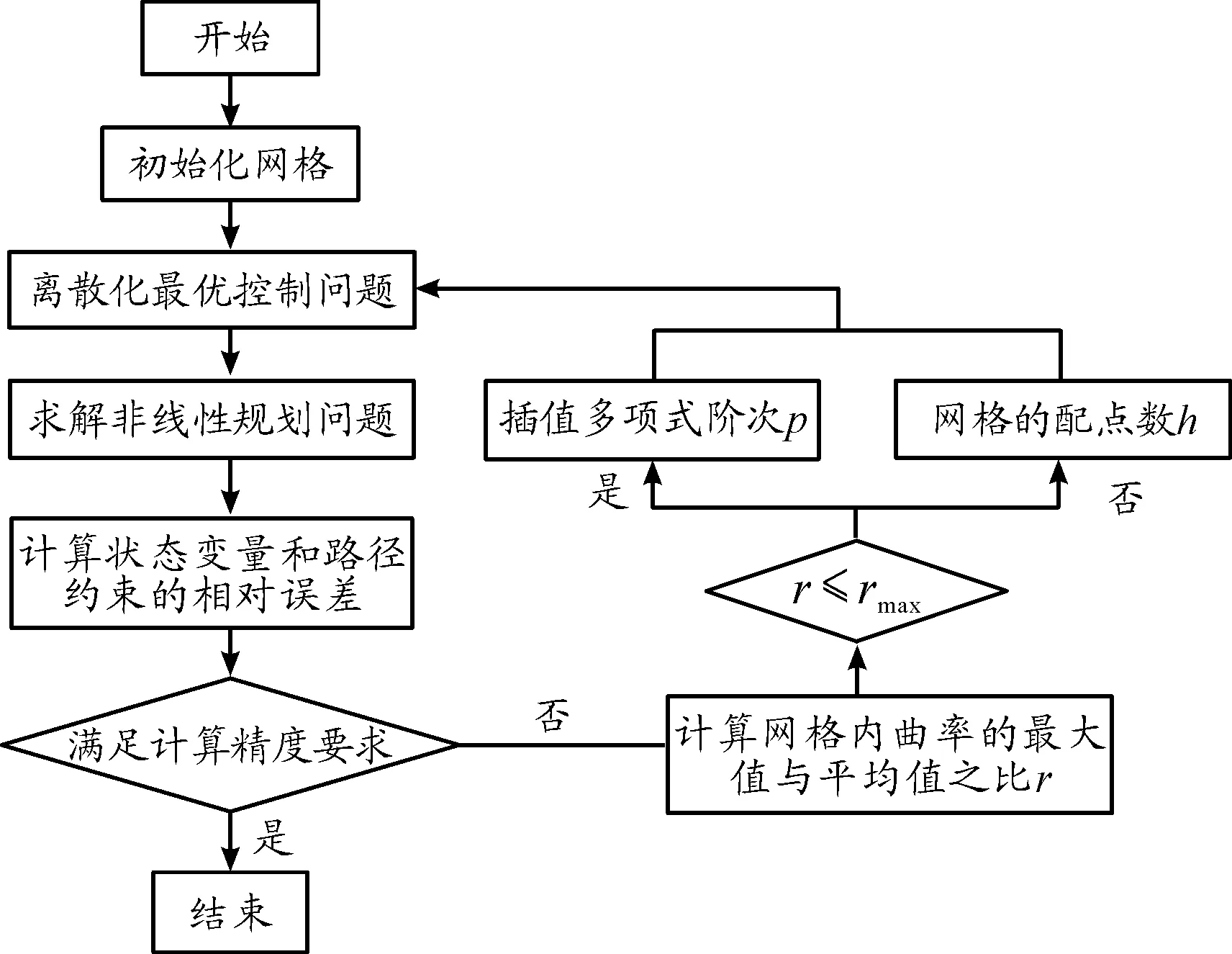
图3 hp自适应伪谱法的计算流程

2 主动学习Kriging模型

2.1 Kriging模型

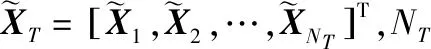
(3)

式(3)中，f(X)=[f1(X),f2(X),…,fn(X)]T为回归基函数，n为回归基函数的个数，β=[β1,β2,…,βn]T为对应的回归系数，该项对模型进行全局性近似；z(X)为服从高斯分布N(0,σ2)的随机过程，该项对模型进行一定程度的修正[15]。

利用对数似然函数，给出回归系数β及方差σ2的极大似然估计

(4)

(5)

其中，F=[f(X1),f(X2),…,f(XNT)]T是f(X)的向量，R为相关矩阵[16]。

在某一未知不确定性因素影响下，Kriging模型在给出预测射程的基础上，还可以进一步给出预测射程的预估标准差，服从如下高斯分布

(6)

式(6)中，μD(X)为Kriging的预测射程，σD(X)为预测射程的预估标准差。

2.2 主动学习策略

根据识别的不确定性干扰因素分布类型及其分布参数，在整个不确定性空间选取一定数量的Monte Carlo样本点集XMC，样本点数量Nc要求满足相关系数小于0.05，即

(7)

根据Kriging模型服从高斯分布的特性，样本点集XMC中任意点分类失效概率可表达为如下：

(8)

其中，U函数为学习函数，当U函数较小时，分类失效概率π较大，在当前Kriging模型下，该样本点具有较大不确定性。进而，在样本点集XMC中选取U函数最小值对应的样本点作为序贯新增训练点，即选取最大分类失效概率的样本点。

通过上述主动学习策略，序列加点，自适应更新Kriging模型，若在迭代过程中，U函数的最小值大于2时，此时样本点集XMC的最大分类失效概率小于Φ(-2)≈0.022 8，满足射程概率评估精度要求，判定收敛。基于主动学习Kriging模型的飞行器射程概率评估计算步骤如下：

1) 根据识别的飞行过程不确定性干扰因素分布类型及分布参数产生样本点集XMC。

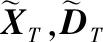
4) 利用Kriging模型计算U(XMC)，选取最小值min(U(XMC))对应的样本点为新增训练点Xnew。

5) 若min(U(XMC))>2，Kriging模型满足精度要求，完成飞行器射程概率评估计算；否则，继续步骤6。

3 数值仿真

以固体火箭发动机助推CAV构型飞行器方案为基准，CAV构型飞行器质量为907.18 kg，气动面积为0.483 87 m2，目标射程为1 300 km。若在不确定性因素影响下射程可信程度大于95%，即满足设计要求；否则，修改论证方案直至满足射程概率评估条件。主要参数如表1所示。

表1 基线方案主要标称参数

忽略不确定性因素影响，利用零维内弹道方程组给出标称状态下压力-时间曲线p(t)以及推力-时间曲线T(t)，如图4所示。进而，给定弹道终端约束为终端高度20 km，终端速度1 000 m/s，终端弹道倾角-23°，利用hp自适应伪谱法给出标称状态下射程最大的纵程-高程曲线d(h)以及速度-时间曲线v(t)，如图5所示。

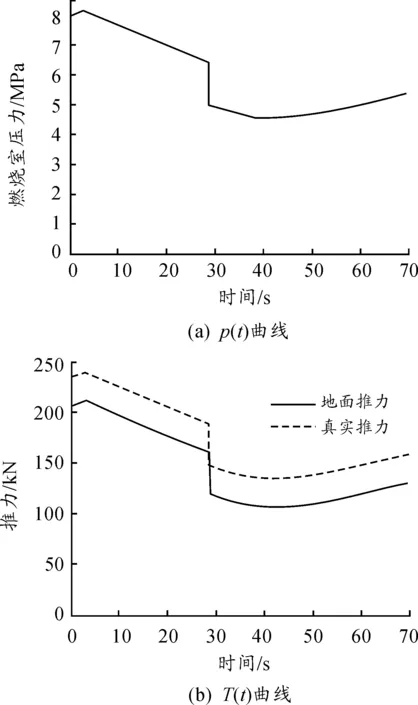
图4 发动机压力-时间p(t)和推力-时间T(t)曲线

通过仿真计算，标称状态下最大射程达到了1 510 km，与目标射程1 300 km相比预留210 km裕度，为验证上述射程裕度的合理性，开展射程裕度精细化评估。结合飞行器弹道特点以及工程经验，考虑如下不确定性因素，包括助推段发动机推力偏斜θ、助推段发动机推力系数偏差ΔP，气动升力系数偏差ΔCl，气动阻力系数偏差ΔCd以及滑翔弹头质量偏差Δm，其不确定性干扰因素分布类型及分布参数值如表2所示。

图5 弹道的纵程-高程d(h)以及速度时间v(t)曲线

不确定性因素分布类型分布参数θ/(″)正态分布N(0,1.5)ΔP均匀分布U(-0.03,0.03)ΔCl均匀分布U(-0.15,0.15)ΔCd均匀分布U(-0.15,0.15)Δm/kg正态分布N(0,3)

根据识别的不确定性因素模型随机选取10 000个Monte Carlo样本点，利用拉丁超立方采样方法抽取21个训练点构建初始Kriging模型，进而采用主动学习Kriging方法开展射程概率评估，通过154次序列加点，自适应更新代理模型，满足收敛条件。进一步给出加点射程响应与目标射程之差的迭代历程如图6所示。

通过图6表明：基于主动学习Kriging的飞行器射程概率评估方法趋于选择目标射程附近的样本点以及不确定性因素较大的样本点，因而，Kriging模型在目标射程附近具有较高的精度，满足射程概率评估需求，为进一步验证方法的准确性和有效性，采用常规的Monte Carlo方法开展射程概率评估，评估结果如表3所示，其中计算仿真平台的处理器为Intel(R) Core(TM) i7-6700U CPU @3.40GHz,内存4.00GB。

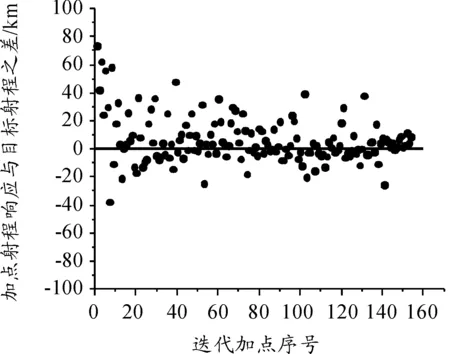
图6 加点射程响应与目标射程之差的历程

由表3可见，基于主动学习Kriging的飞行器射程可信程度与Monte Carlo方法结果的相对误差不足0.5%，具有很高的计算精度。同时，本文方法调用射程仿真次数远小于Monte Carlo方法的分析次数，具有较高的计算效率，满足方案阶段快速设计迭代的工程需求。此外，分析结果表明，飞行器基线方案的射程可信程度大于95%，满足射程指标需求，实现了射程裕度的量化分析计算。

表3 飞行器射程概率评估结果

4 结论

针对临近空间高超声速飞行器大空域、宽速域的特点，在建立气动、推进、质量、弹道学科分析模型的基础上，通过考虑飞行过程不确定性因素的影响，建立了飞行器射程概率评估模型，实现了射程裕度的定量评估。在此基础上，通过引入主动学习策略和Kriging代理模型提升了射程评估效率，结合数值仿真结果验证了该方法的准确性和有效性，减少了射程评估的计算时间，为飞行器总体方案射程评估提供定量依据，具有较强的工程实践意义。