多弹协同微分对策制导律研究

郭志强,周绍磊

(海军航空大学， 山东 烟台 264001)

近年来，针对可以利用电磁干扰、假目标欺骗和大机动规避等手段的目标拦截问题引起了制导学者的重视[1-2]。由于微分对策制导律[3-8]在制导过程中不需对目标的机动规律作任何假设，只需考虑目标的机动能力，因而可使目标机动对制导精度的影响降到最小。本文根据多个拦截弹协同拦截单个机动目标的对策模型和制导要求，基于微分对策理论提出了一种协同制导律，该制导律选用了适用于所有对策参与者的性能指标，不需事先选择相关的权值[9]，避免了对非连续性能指标泛函的处理。

1 运动模型及其简化

1.1 非线性运动模型

本文考虑多个拦截弹协同拦截一个机动目标进行到末制导阶段时的情况，并在制导律的推导过程中做出以下假设：

1) 拦截弹和目标均具有理想动力学特性，且在运动中均可视为质点；

2) 拦截弹和目标的速度均为常值，且其相对运动可在初始视线方向附近线性化；

3) 重力因素可忽略，且拦截弹和目标的制导问题可以在俯仰平面和偏航平面内解耦。

m个拦截弹与单个目标的平面相对运动关系如图1所示，图中XI-OI-YI表示惯性坐标系，Mi表示第i(i=1,2,…,m)个拦截弹，T表示目标。V、a和γ分别表示速度、法向加速度和航向角，变量的下标i和T分别相应于拦截弹Mi和目标T，LOSi0表示拦截弹Mi与目标之间的初始视线，λi0(λi)表示拦截弹Mi与目标之间的初始视线角(视线角)。

根据图1所示的相对运动关系，可得极坐标下各拦截弹与目标的相对运动方程为

(1)

每个对策参与者各自的动力学方程可表示为

(2)

式中：xj=[xj1xj2…xjnj]T表示每个对策参与者的内部状态向量；uj为其控制指令，根据假设1)有aj=uj；各自状态向量的维数为dim(xj)=nj。

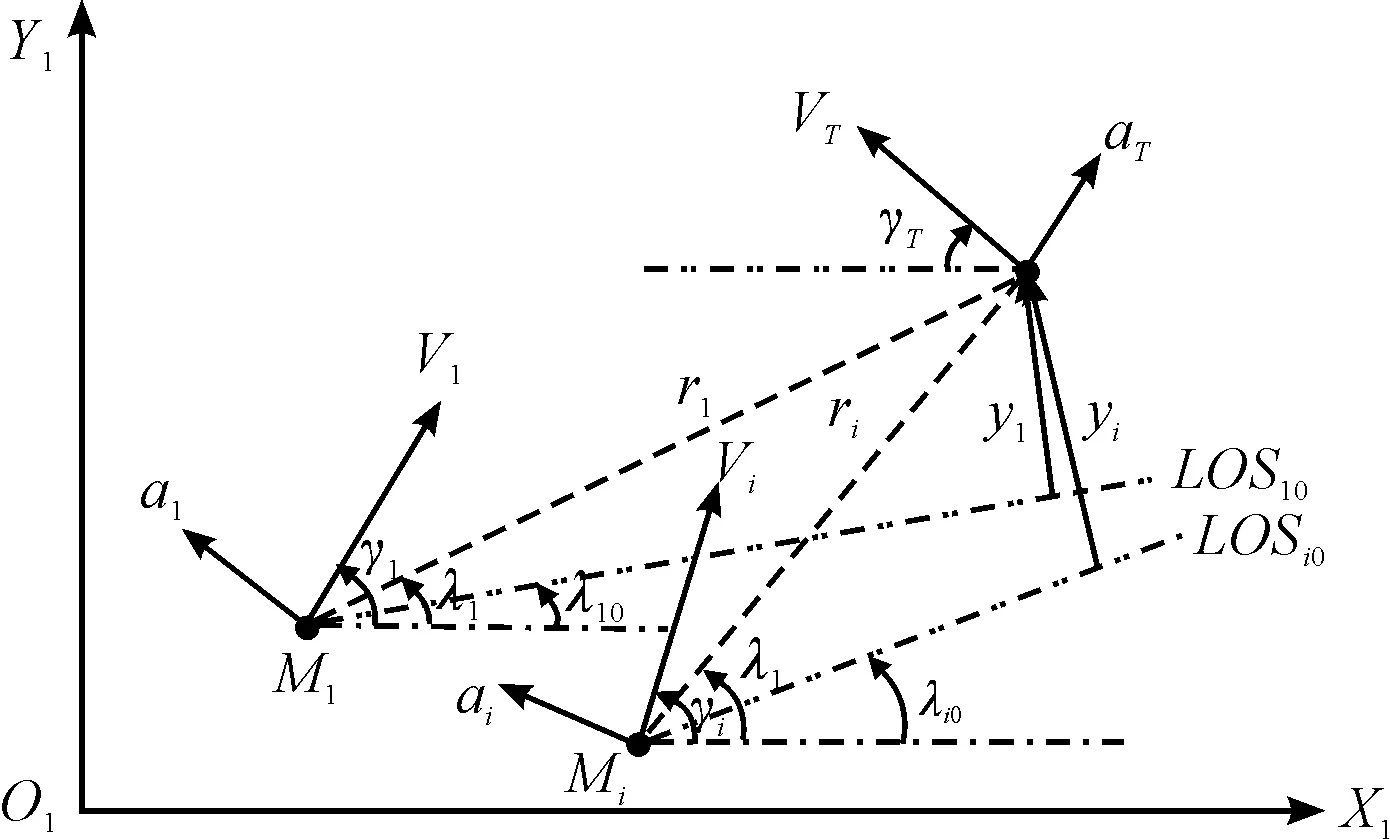
图1 拦截弹-目标的平面相对运动关系

1.2 系统线性化

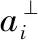
(3)

(4)

将对策各方所组成系统的状态向量表示为

(5)

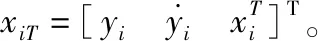
(6)

将式(6)写成矢量形式则有

(7)

式中：A、B和C为适当的矩阵。

1.3 系统降阶

由系统运动方程可以看出，系统维数

dim(x)=n1+…+nm+nT+2m

(8)

显然，当系统维数庞大时对问题进行求解是十分繁琐的。为了对系统进行降阶，通过变换引入新的变量——零控脱靶量Zi(t)

Zi(t)=DiΦ(tfi,t)x(t)

(9)

式中：t为当前时刻，Φ(tfi,t)为系统状态转移矩阵，tfi为拦截弹Mi的终端拦截时刻。矩阵Di称为状态提取矩阵，其形式如下

(10)

拦截弹的终端拦截时间可近似表示为

(11)

在这里本文将对策结束时间定义为

tf=min{tf1,tf2,…,tfm}

(12)

新引入的零控脱靶量组成的向量可表示为

(13)

将其作为新的系统状态向量，则系统维数可降至dimZ(t)=m。

对零控脱靶量求关于时间的导数可得

(14)

1.4 性能指标泛函

微分对策性能指标的选取主要有两种类型，一种是直接采用零控脱靶量作为性能指标的范数型微分对策，另一种是采用线性二次型的性能指标。由于采用范数型微分对策所得到的制导律为“bang-bang”型控制律，不能充分发挥中间控制能量的最优性[10]，本文则根据零控脱靶量，为每个对策参与者选择共同的二次型性能指标泛函如下

(15)

其中，αi、βi均为非负系数。αi表示对拦截弹脱靶量的约束，当αi→∞时表示拦截弹将获得理想拦截对策(即终端脱靶量为零)；βi表示对拦截弹控制能量的约束。此时拦截弹与目标构成了线性二次型微分对策，拦截弹之间采取协同机动使性能指标J极小(也即使脱靶量极小的同时希望使所消耗的能量最小)，而目标则努力使性能指标J达到极大。

2 制导律设计

为简单计，下面将针对两个拦截弹协同拦截单个机动目标的情况进行分析，此时对策变为最简单的情形——二对一追逃微分对策。

性能指标可写为

(16)

该最优问题的哈密顿函数为

(17)

根据最优控制理论可得系统的伴随状态

λ1(t)=α1Z1(tf);λ2(t)=α2Z2(tf)

(18)

在对策过程中，参与对策的各方采取机动，使得下式成立

(19)

则根据控制方程

(20)

可得三者的开环最优控制为

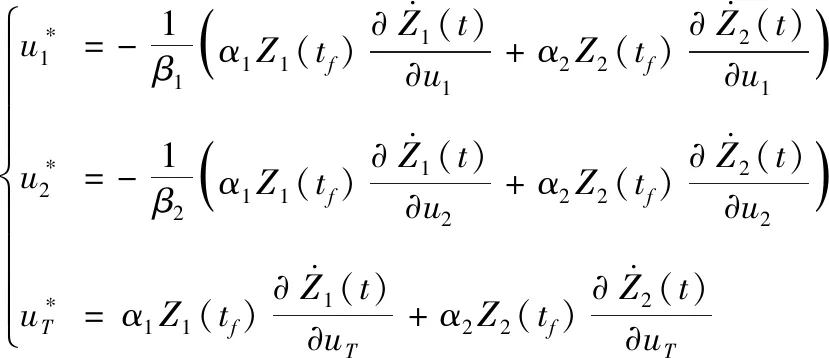
(21)

又由式(9)、式(10)可得零控脱靶量及其导数分别为

(22)

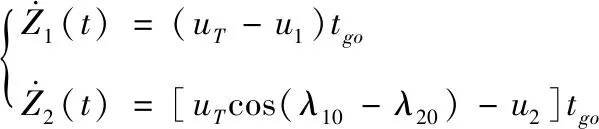
(23)

将式(23)代入式(21)可得

(24)

将式(24)代入式(23)，并分别从t到tf积分可得两个耦合的方程，解之可得

(25)

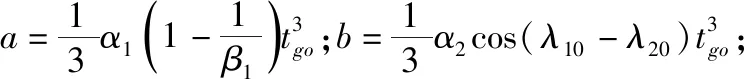
将式(25)代入式(24)，可得相应的闭环最优解为

(26)

其中

(27)

式中：Δ=(1-a)(1-d)-bc。容易看出，该微分对策问题的鞍点存在的充分条件为Δ≠0。

对于式(22)，根据小偏差假设则有

(28)

对上式求关于时间的导数后再代入式(22)可得

(29)

至此，式(26)所示的协同微分对策制导律设计完毕。本文通过为每个对策参与者选取共同的性能指标，有效避免了对分段连续性能指标泛函的处理，无需在制导律的初始阶段选取较多的权值，得出了适合在线应用的制导律。

3 仿真分析

本节针对两个拦截弹迎击拦截单个大机动目标的情况对所设计的制导律进行仿真分析。仿真参数值如表1所示。

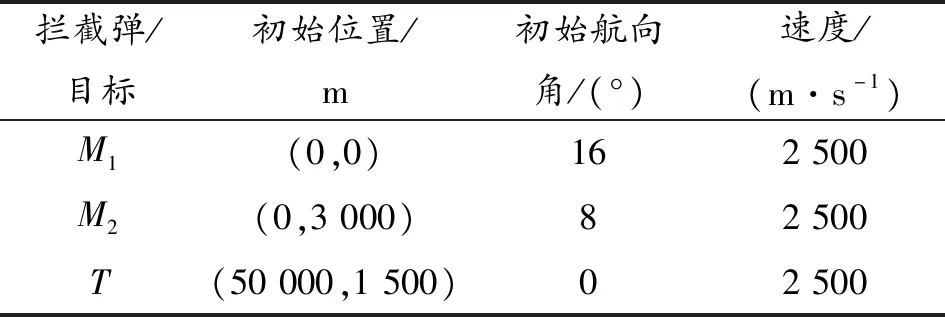
表1 仿真参数值

两枚拦截弹采用本文提出的制导律协同拦截单个目标，仿真过程的有关系数取为α1=α2=108，β1=β2=2，仿真结果如图2～图5所示。

由图2和图3表明，利用本文所设计的制导律，拦截弹M2在拦截弹M1的协同配合下首先命中目标。由于本文及文献[10]的制导方法均非时间上的协同制导，均未对制导时间做约束，故在对策结束时拦截弹M1与目标之间尚有一定距离，但这一距离并非其最终的脱靶量。

图4表明，当拦截弹和目标均采用最优机动策略时，拦截弹可以以较低的加速度需求完成拦截任务(a1max≈47 m/s2，a2max≈58 m/s2，aTmax≈206 m/s2)，这说明通过采用本文制导律，拦截弹以较低的机动通过协同配合完成对高机动目标的拦截。

下面在表1给出的参数条件下，对两枚拦截弹采用文献[10]提出的CLQDG协同制导律的情况进行分析。仿真中CLQDG方法的相关参数选取为α=105，αE=105，该方法中权重系数k的取值为0.5，其结果如图5-图7所示。

图5和图6表明，在CLQDG方法中拦截弹M2率先命中目标。图7为采用CLQDG制导律时拦截弹和目标的控制指令(a1max≈157 m/s2，a2max≈151 m/s2，aTmax≈295 m/s2)。

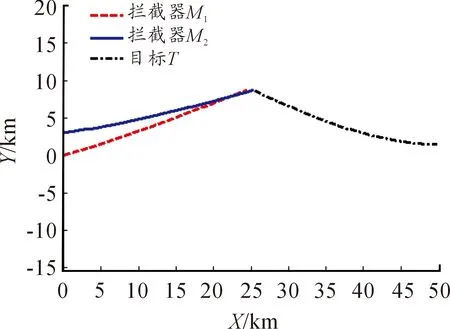
图2 拦截弹与目标的运动轨迹

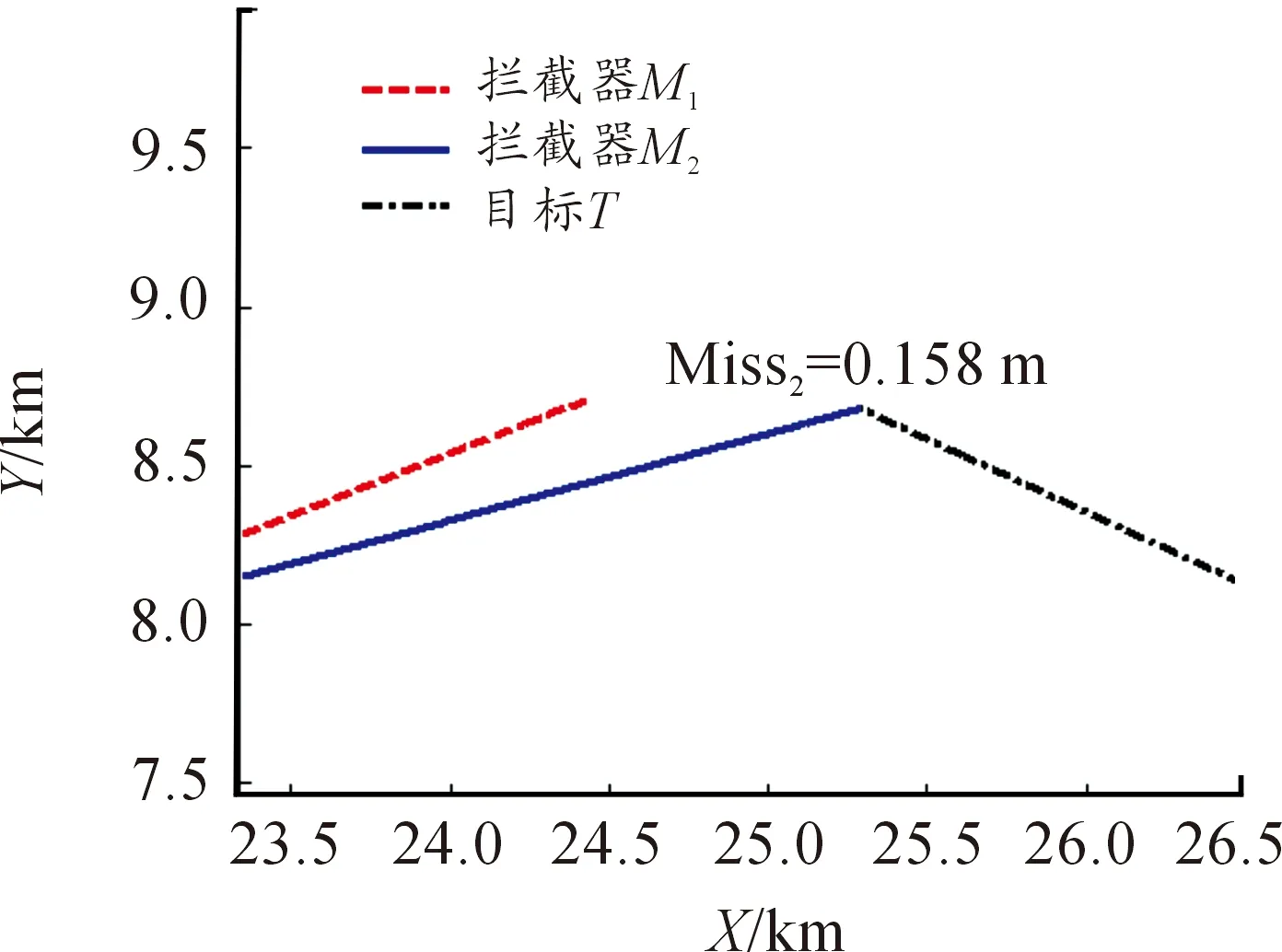
图3 拦截弹与目标的运动轨迹(放大图)

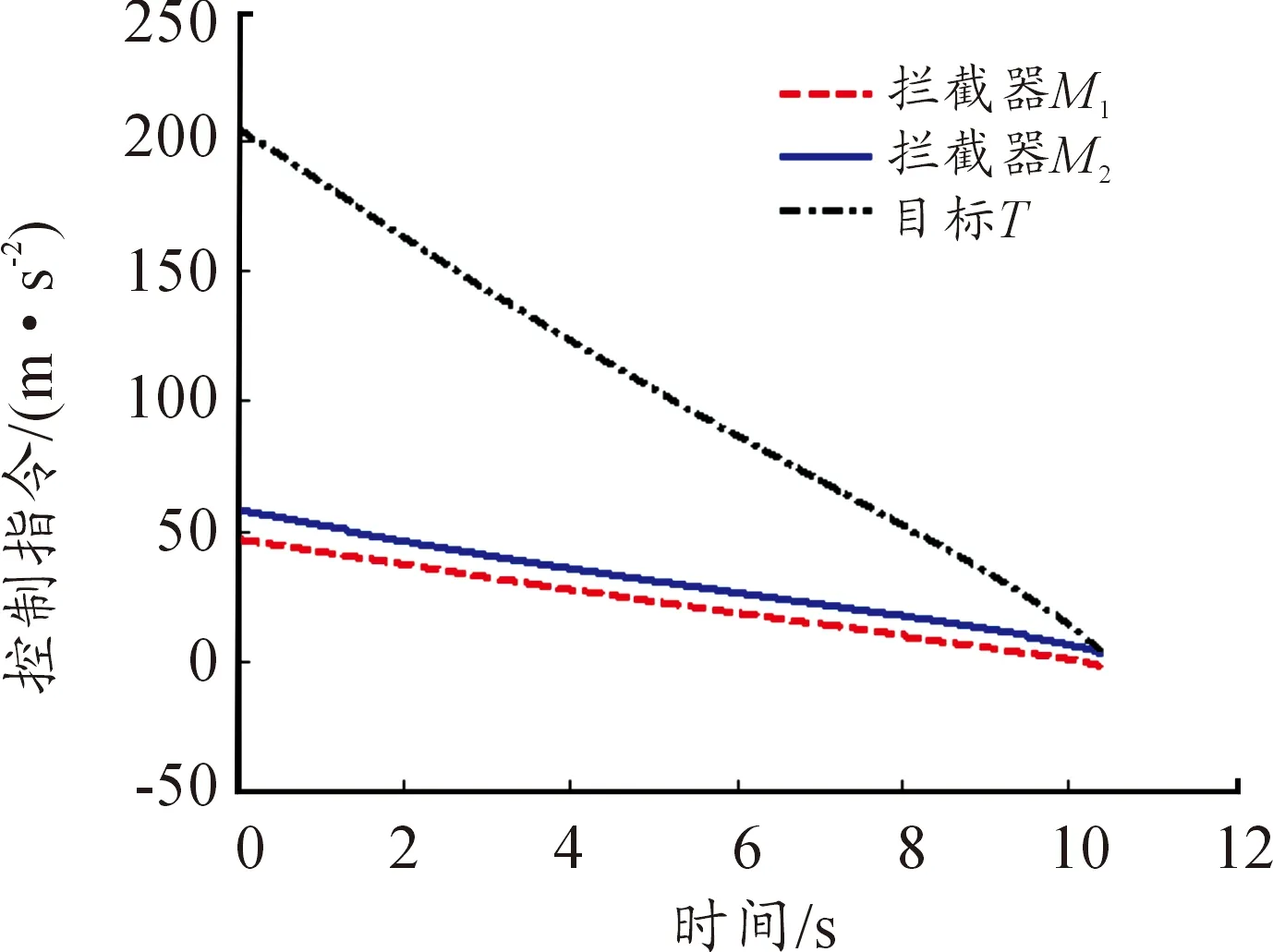
图4 拦截弹与目标的控制指令

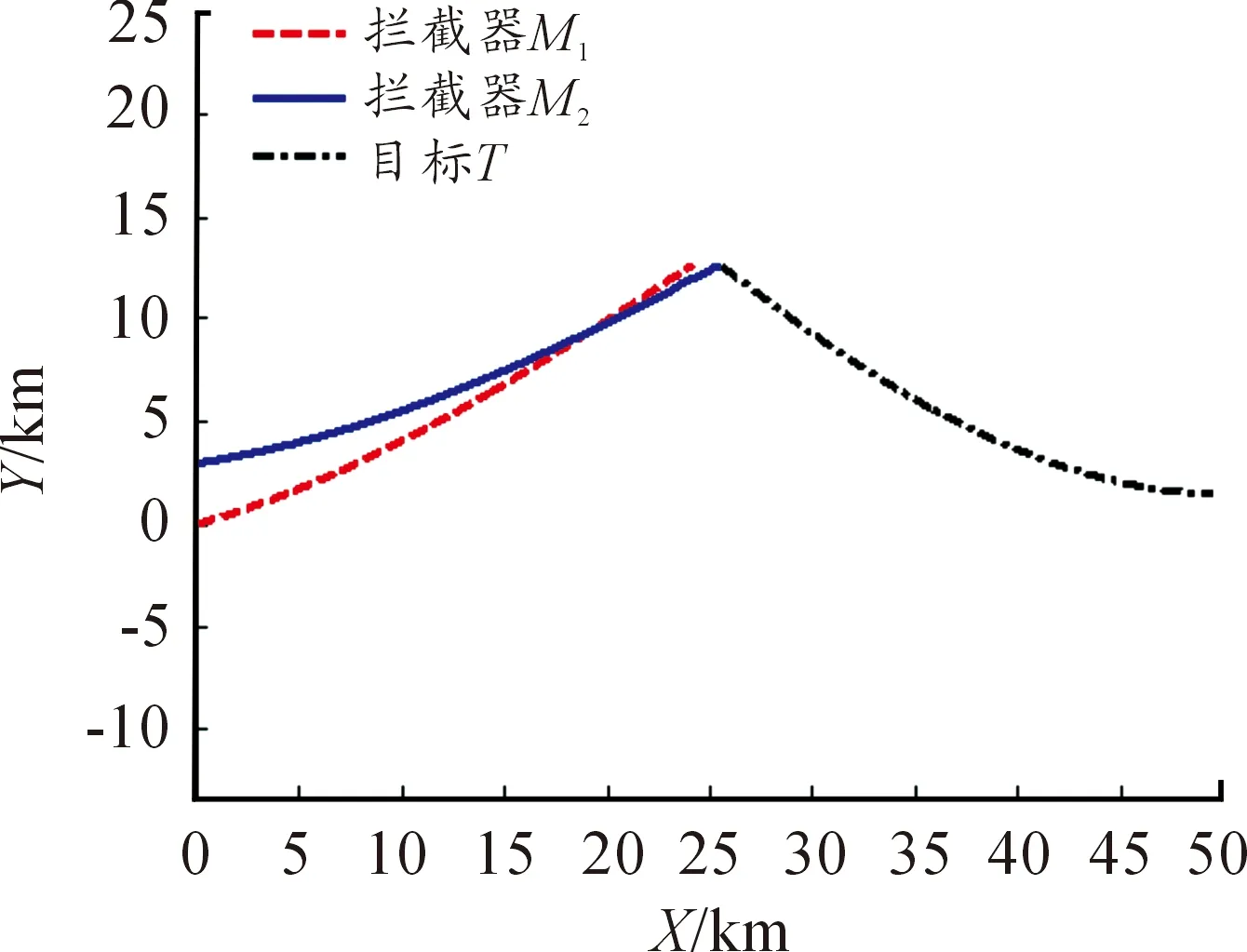
图5 拦截弹与目标的运动轨迹-CLQDG

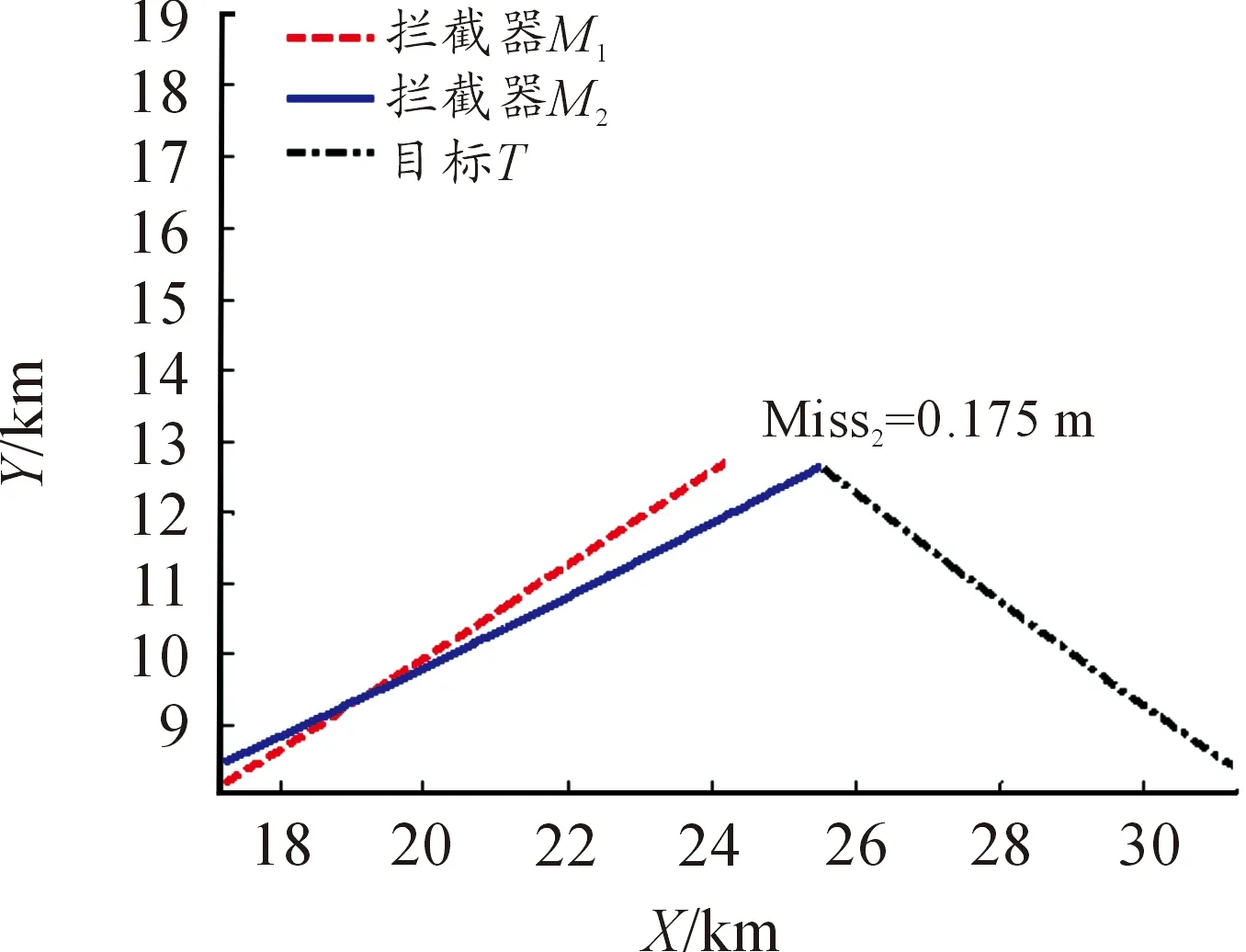
图6 拦截弹与目标的运动轨迹-CLQDG (放大图)

由以上仿真结果可以看出，采用两种制导方法均能对目标进行拦截，但本文所提方法不涉及对分段函数的处理，而且拦截弹完成拦截所需的加速度需求减小，从而降低了对拦截弹的机动性要求，实现了对高机动目标的拦截。

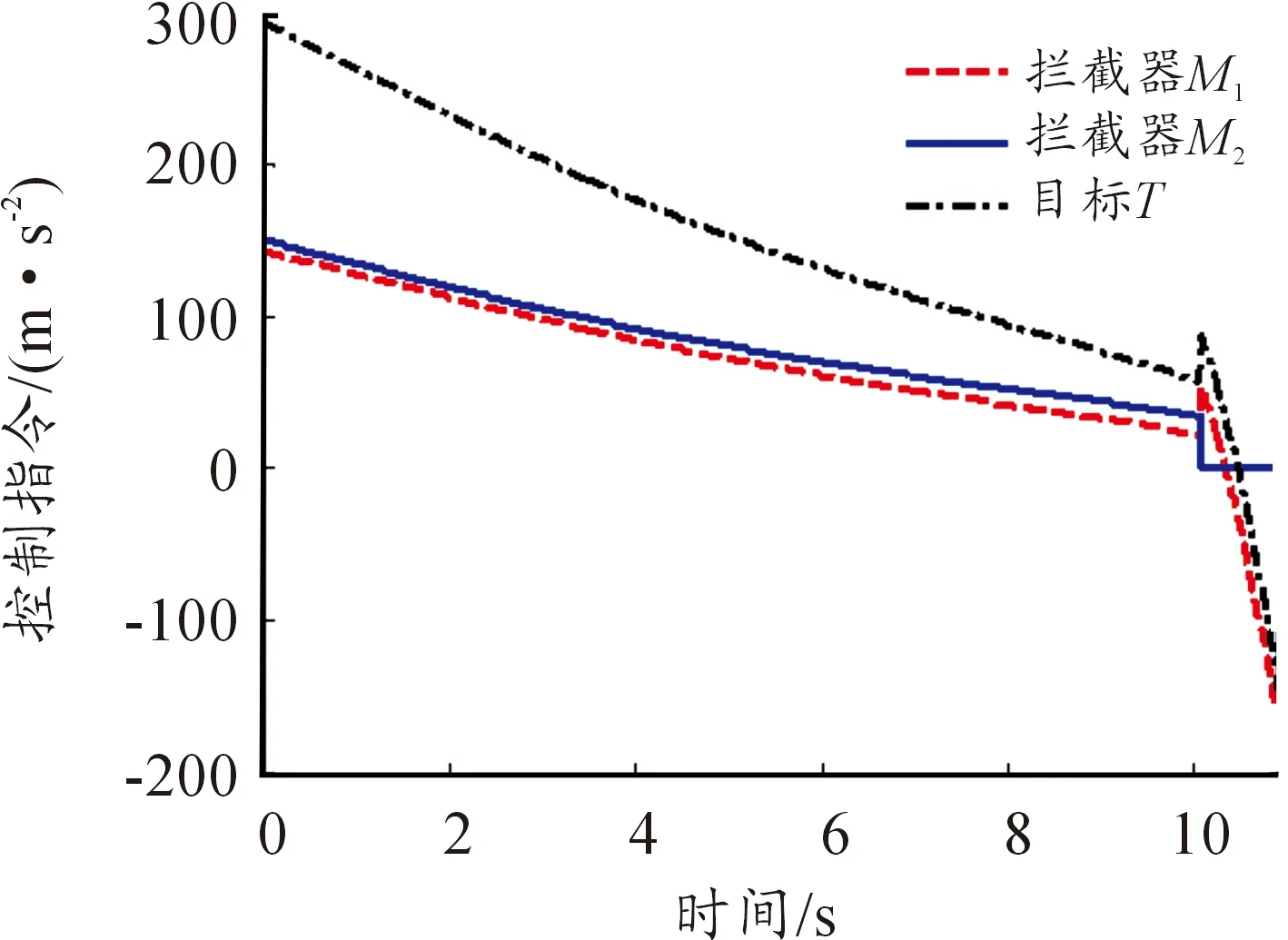
图7 拦截弹与目标的控制指令-CLQDG

4 结论

考虑到当追逃双方分别采用不同的性能指标时，要涉及到分段函数的处理以及相关参数的事先选取，为了避免这些问题，本文基于微分对策理论，选取了适用于所有对策参与者的性能指标，进一步推导出对策双方的闭环最优制导策略。在对策过程中，各拦截弹在追求自身脱靶量最小的同时，采取协同机动以减小其他拦截弹的脱靶量，通过仿真分析表明了本文所提制导律的有效性。