子母弹中心管式静态抛撒仿真技术研究

许胜刚，蔡汝山，李 劲

(工业和信息化部电子第五研究所， 广州 510610)

在子母弹的研究过程中，子母弹抛撒系统的研究是关键部分之一[1]。目前应用的抛撒系统主要有燃气活塞式、气囊式、中心管式等等。其中，中心管式抛撒系统因具有抛撒系统紧凑、子弹药初速高等优点而被广泛应用。美国的MLRS火箭系统使用的是中心爆管抛撒技术，每发母弹携带644枚子弹药，圆柱部外圈排列14枚子弹药，内圈排列7枚子弹药，子弹串之间用聚碳酸酯塑料固定并隔离，在母弹中心部位装有药管。当母弹被发射出到达指定作战区域后，母弹时间引信作用，引爆中心爆管，冲击波挤压母弹壳体，母弹壳体开裂，同时将子弹药向四周抛出。中心管式抛撒方式的抛撒过载非常大，较大的抛撒过载易造成子弹药弹体变形和引信变形。弹体变形将造成子弹药落地姿态较差，导致子弹药引信失效；引信变形易造成安保装置未解保、发火机构失效等，这些均会造成子弹药瞎火。因此，采用中心爆管式抛撒技术的子弹药瞎火率往往较高。南京理工大学钱华梅[2]设计了一种高抛速、低过载的多用途航空子母弹二次抛撒系统，该抛撒系统可以在满足抛撒指标的前提下，将抛撒过载控制在较小的范围内。在中心管式抛撒技术的研究中，进行静态抛撒研究十分关键。通过静态抛撒研究，可以确定中心管式抛撒药的种类和装药量，研究子弹药在抛撒过程中承受的过载，对子弹药的强度进行校核，获得子弹药的抛撒速度及落地分布。目前，针对中心管式静态抛撒的研究较少。本文建立了子弹药静态抛撒的内弹道模型，对其内弹道过程进行了数值模拟仿真，得到了子弹药内弹道过程的运动学参数变化规律。

1 物理模型

如图1所示，子母弹静态抛撒使用的是专门研制的模拟母弹，在其内壁上设置有预制槽，用于放置子弹药串，同时，预制槽也是便于母弹壳体破裂。装配有子弹药的模拟母弹实物如图2所示，子弹药套装成串后，按串装入母弹，以中心爆管为中心，圆周排列，子母弹系统示意图如图3。

图1 静态抛撒用的模拟母弹

图2 装配有子弹药的模拟母弹实物

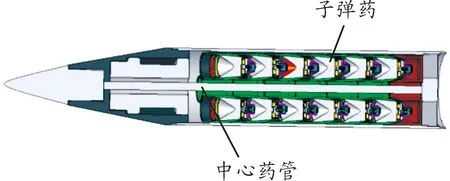
图3 子母弹系统示意图(纵截面)

中心药管是抛撒装药的燃烧室。中心药管中装有电点火头、电雷管和抛撒用发射药。集束子弹药抛撒过程是复杂的，包括了抛撒药燃烧、中心管爆裂、子弹运动、母弹壳体破裂等多种现象。静态抛撒时，电点火头工作，点燃中心药管内抛撒药，抛撒药燃烧释放出高温高压气体，当管内的气体压力超过管本身的承压强度极限时，中心药管爆裂，抛撒药的燃气压缩子弹药挤压母弹壳体。随着抛撒药的燃烧，母弹腔内压力不断增加，子弹药将母弹壳体挤压破裂，子弹药解除约束。随后，子弹药在中心药管高温、高压、高速的燃气的作用下沿着径向向四周运动，最终子弹药抛撒出母弹。

2 子弹药静态抛撒内弹道数学模型

2.1 内弹道过程基本假设

子弹药静态抛撒过程是将抛撒药的化学能转化为子弹药动能的过程，该过程非常短暂，为方便建立内弹道数学模型，提出如下假设[1,3-5]：

1) 抛撒药的燃烧满足几何燃烧定律，在中心管式抛撒药燃烧过程中，没有未燃烧火药流出，抛撒药的燃烧速度为中心管或子弹药后方平均压力的指数燃速函数。

2) 抛撒药燃气服从诺贝尔方程，火药力、余容、比热比等为常数，燃气与未燃烧的火药在各自区域内均匀分布，燃气流动为等熵流动。

3) 当中心药管内的压力达到其爆裂压力时，管壁沿轴向同时炸开，子弹药运动取轴对称一维模型，不考虑炸开过程及沿轴向炸开的不同时性，不考虑中心药管破片对子弹药运动的影响；仅考虑子弹药与火药气体的径向运动。设定子弹药轴向运动分量为零，将所有子弹看成一个整体，均匀分布于中心药管的侧面，对弹丸的推力面积假设为圆柱体的有效侧面积，不考虑弹后压力分布给子弹运动带来的影响。

4) 火药的热量散失用气体流失系数 来修正，除子弹药运动以外的次要功用次要功系数 来修正。

2.2 内弹道数学模型

根据经典内弹道学理论，中心管式抛撒药燃烧方程为：

(1)

抛撒药形状函数[6]：

(2)

式(2)中:z为抛撒药相对已燃厚度，u1为抛撒药燃速系数，e1为抛撒药初始弧厚的一半，p1为平均压力，ψ为抛撒药已燃百分比，χ、λ、μ为抛撒药形状的特征量，zk为抛撒药燃烧结束时相对已燃厚度，n为抛撒药燃速指数。

火药燃烧为定容燃烧，其定容气态方程为

(3)

式(3)中：f为抛撒药的火药力，ω为抛撒药装药总质量，p1为抛撒药压力，V0为中心管容积，ρ为抛撒药密度，β为火药余容。

子弹药所受压力与其速度关系为

(4)

子弹药位移和速度关系为

(5)

式(5)中：pf为母弹壳体对子弹药的压力，S为抛撒药有效作用面积，φ0为虚拟质量系数。m为单个子弹药质量，N为子弹药个数，s为子弹位移。

火药气体具有的状态势能为

(6)

式(6)中：φ1为火药气体流失修正系数。

子弹药动能为

(7)

式(7)中：φ2为次要功系数。

某一瞬间火药燃烧释放出的总能量为

E=φ1fωψ

(8)

能量守恒方程为

E=Ep+Ek

(9)

即：

(10)

式(1)～式(5)、式(10)联立，构成子弹药静态抛撒内弹道数学模型。

3 静态抛撒过程仿真

3.1 内弹道数学模型

实际子弹药抛撒装置较为复杂，不便于建立仿真模型。对子弹药抛撒装置进行合理简化，忽略其中部分非重要的结构，建立其静态抛撒仿真模型，如图4所示。

图4 装配有子弹药的母弹实物静态抛撒仿真模型

在该模型中，子弹药和中心药管外壳采用横向各异性硬化塑性材料模型[6]，其材料参数设置如表1和表2所示[7]。

表1 子弹药模型参数

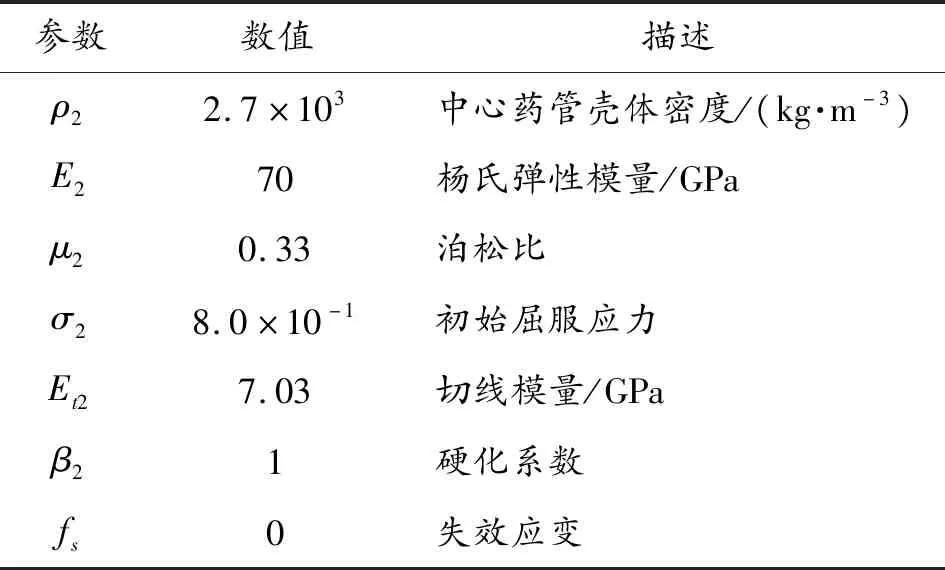
表2 中心药管模型参数

火药用高速爆炸燃烧材料和线性多项式状态方程模拟[7]。空气模型用流体空材料和线性多项式状态方程定义[8]，其压力表示为

P=C0+C1μ+C2μ2+C3μ3+

(C4+C5μ+C6μ2)E

(11)

其中，μ=1/V-1。式(11)中，C0至C6为状态方程系数，E为空气单位体积内能，V为相对体积。对于空气模型，C0=C1=C2=C3=C6=0,C4=C5=0.4.空气密度取ρ3=1.29 kg/m3，初始相对体积V0取1。

3.2 仿真算法

有限元分析中，计算固体力学多采用Lagrange方法，计算流体力学多采用Euler方法，在计算流固耦合问题时，需要选用一种兼备两种算法优点的算法，即Arbitrary Lagrange-Euler(任意拉格朗日-欧拉)算法，简称ALE算法[9]。子弹药静态抛撒过程涉及中心药管起爆、抛撒药燃烧、子弹药在抛撒药的燃气作用下挤压母弹壳体等过程，是一个典型的流固耦合问题。因此，该仿真过程需使用ALE算法。

在子弹药静态抛撒仿真中，抛撒药网格采用单点ALE多材料体单元，抛撒药网格周围用空气填充，空气网格也采用单点ALE多材料体单元。中心药管采用壳单元网格划分，耦合在抛撒药和空气组成的Euler场中。子弹药采用Lagrange算法，采用固体单元划分。空气的上下边界采用非反射边界，以保证计算的精度[10-11]。

3.3 仿真结果及分析

利用ANSYS/LS-DYNA对抛撒模型进行数值模拟仿真，设置总的计算模拟时间为5.4 ms，得到静态抛撒过程中子弹药运动规律曲线，如图5～图7所示。

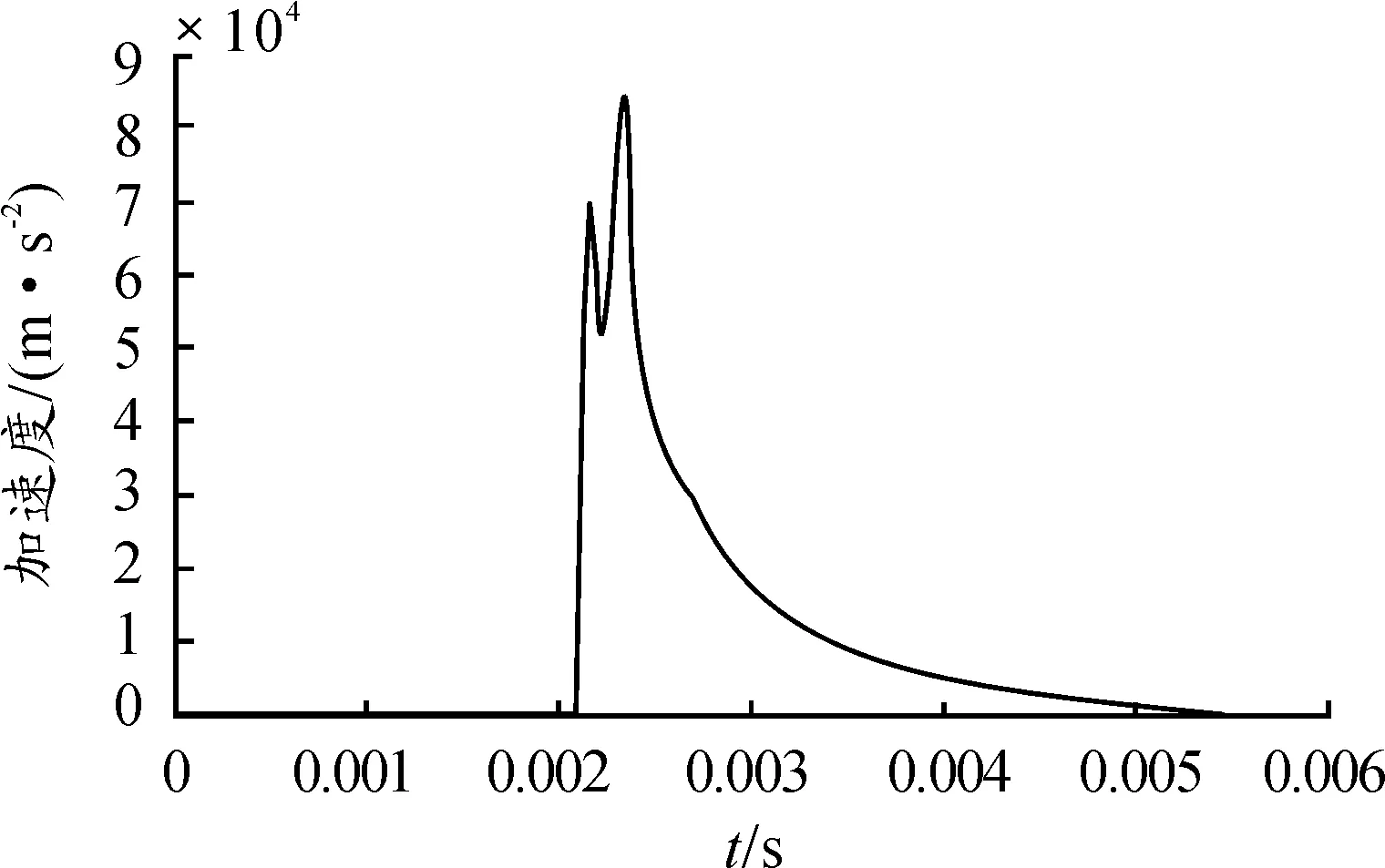
图5 子弹药加速度曲线

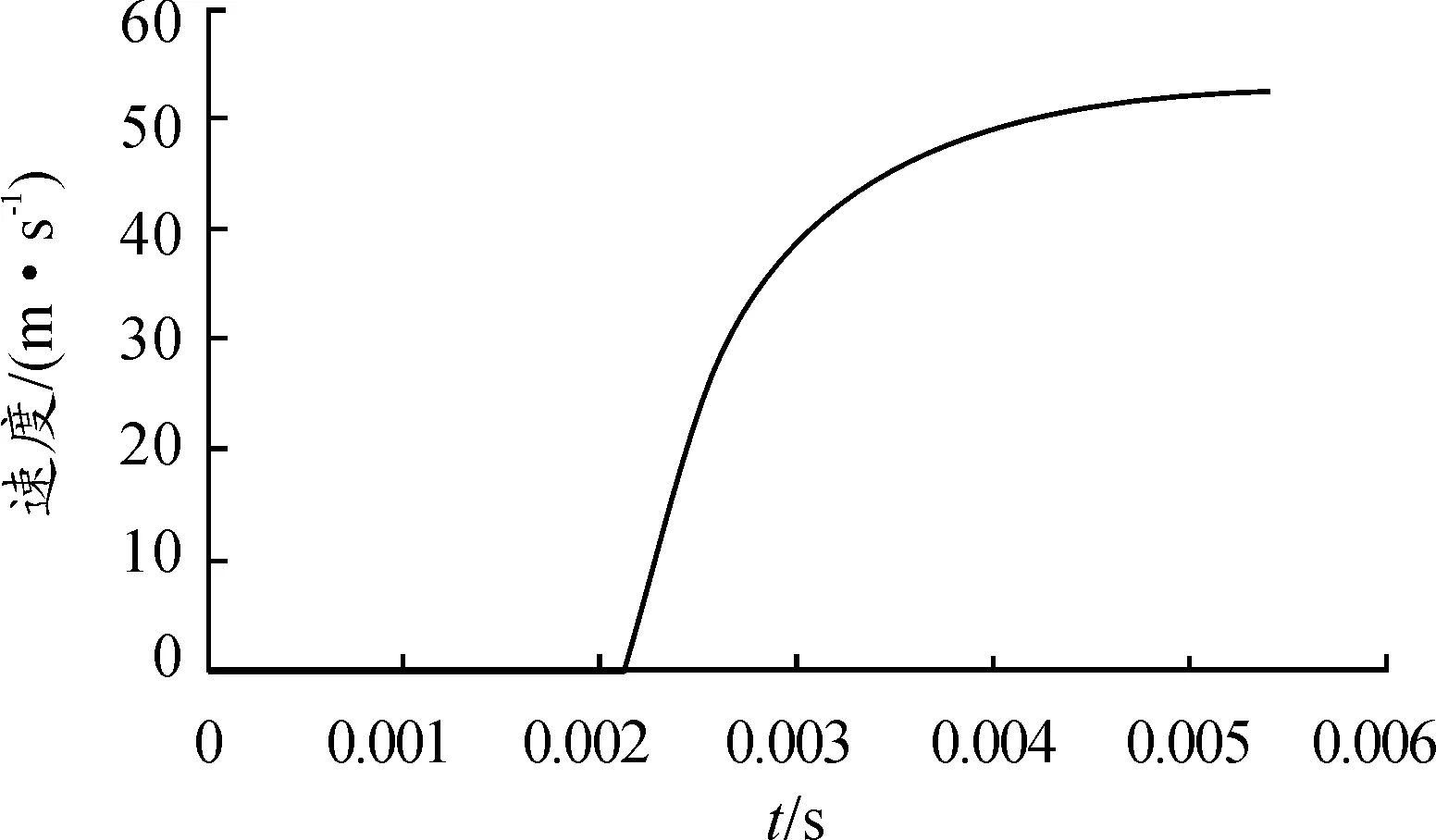
图6 子弹药速度曲线

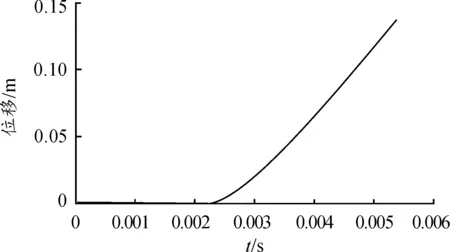
图7 子弹药位移曲线

由图5可以看出：在抛撒药压力和母弹壳体反作用力的综合作用下，子弹药在中心药管起爆后2.1 ms之前没有获得加速度，随后子弹药加速度增加，最大值为8.5×104m/s2，之后子弹药加速度下降，最后降为0。母弹壳体的破裂过程对子弹药加速度的影响较大，这导致了子弹药加速度在增加的过程中出现了波动。

由图6可以看出：在2.1 ms之前，子弹药未获得速度，之后子弹药速度逐渐增加，被抛出时子弹药速度为52.5 m/s。子弹药静态抛撒试验中，子弹药抛出的速度为50～60 m/s。

由图7可以看出：在2.1 ms之前，由于母弹壳体的挤压，子弹药未发生位移，在2.1 ms之后，母弹壳体破裂，子弹药在抛撒药压力的作用下，逐步抛离母弹，当抛撒药压力消失时，子弹药产生137.5 mm位移。

4 结论

利用本文建立的内弹道模型和数值仿真方法，可实现对中心管式抛撒系统的优化设计，得到所需要的子弹药抛撒速度。本文所建立的子弹药静态抛撒内弹道数学模型对于其他使用中心管式抛撒的弹药同样适用。该模型与子弹药抛撒外弹道模型相结合，建立子弹药抛撒全弹道数学模型，可对子弹药全弹道过程进行分析。