双针床经编机梳栉摆动对瞬时需纱量和纱线张力的影响

徐云龙， 夏风林

(江南大学 教育部针织技术工程研究中心， 江苏 无锡 214122)

在双针床经编机成圈过程中，成圈机构的位置状态不断变化。在不同主轴角度时，成圈机构对纱线的瞬时需纱量也发生着急剧的波动。现有的送经机构还不能保证与瞬时需纱量变化规律同步并送出纱线，因此，经纱需求量与实际送经量之间的差值随着不同成圈阶段而变化，最终导致纱线张力的剧烈波动。纱线张力波动过大会使纱线受损，断纱率上升易形成疵点，严重影响织物品质[1],故研究瞬时需纱量和纱线张力的波动规律十分必要。国内已有对单针床经纱消耗曲线图的研究[2]，以及关于纱线需求量对纱线张力波动影响的讨论[3-4]。国内外学者都认同瞬时需纱量与送纱量之间的差异决定着纱线张力的整体波动趋势和特征[5-6]，但近年来大多数研究基于某种控制器的纱线张力检测与控制[7]以及对纱线与张力补偿装置的动态力学模型分析等[8-9]，没有具体分析梳栉摆动对瞬时需纱量和纱线张力波动造成的影响。

本文重点是测试导纱针-织针、梳栉-织针瞬时需纱量，获得这2种瞬时需纱量变化曲线，对比其变化规律，以深入分析梳栉摆动对瞬时需纱量和纱线张力的影响。

1 实验部分

1.1 设备及仪器

RDJ4/2 EL型(E22)双针床经编机，脱圈板间距为3 mm，前后织针间距为5 mm；使用50.00 mm量程的百分表及拉绳(采用11.1 tex涤纶单丝)测试间隔纱线的瞬时需求量。纱线动态张力测试系统由TS1-200-A2-CE1型张力传感器、分辨率为2 500线的增量式编码器、LMS SCADAS Mobile SCM01型四通道声振分析仪和LMS Test Lab分析软件及计算机组成[10]。

本文测试使用的梳栉纱线为阳离子涤纶(22.2 tex/96 f)，垫纱数码为1-0-0-1//。

1.2 测试方法

1.2.1 瞬时需纱量的测试

1) 搭建瞬时需纱量测试平台，其测试原理如图1 所示。图1(a)所示平台中，百分表安置在机尾位置并与导纱针保持水平，仅测量导纱针-织针瞬时需纱量，等同于导纱针相对静止、针床摆动对纱线的瞬时需求量，用S1(单位为mm)表示；图1(b)所示平台中，百分表安置在后梁位置，用于测试梳栉-织针瞬时需纱量，即成圈机构整体(包括梳栉分纱针)的前后摆动对纱线的瞬时需求量，用S2(单位为mm)表示。拉绳一端固定在百分表测量杆的尾部，另一端穿过导纱针孔与织针连接。

2) 测试方法。在双针床经编机成圈过程中，织针和导纱针之间的拉绳长度不断变化，这些变化会通过拉绳和测量杆反映在表盘刻度上，然后读取百分表数值即为测试结果。无论机速高低，同一角度下的成圈机件都会摆到规定的位置，其对纱线的需求量也是不变的，因此，可测试静态瞬时需纱量。测试时，从经编机主轴0°开始手动旋转慢车电动机，主轴每转动5°记录一次百分表读数，直至转到下一个0°(360°)时即一个横列，完成一次测试。按照以上操作方法分别测试导纱针-织针、梳栉-织针瞬时需纱量，各重复测试3次，计算3次测试的平均值，得出瞬时需纱量的波动曲线。

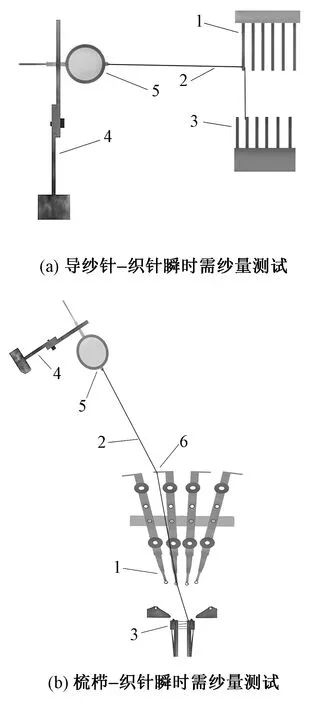
1—导纱针；2—百分表拉绳；3—舌针；4—百分表支架和底座；5—百分表测量杆；6—分纱针。图1 瞬时需纱量测试平台

Fig.1 Testing platform of instantaneous yarn demand. (a) Test for instantaneous yarn demand of guide bar and knitting needle；(b) Test for instantaneous yarn demand of comb and knitting needle

1.2.2 经纱张力的测试

根据分析仪、编码器和张力传感器的连接要求搭建张力测试系统，系统工作原理[10]见图2所示。

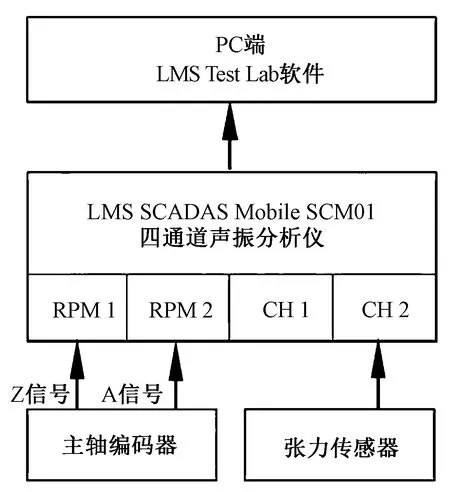
图2 纱线动态张力测试原理图

Fig.2 Measuring principle of yarn dynamic tension

将主轴编码器的Z信号和A信号分别接入分析仪的RPM 1和RPM 2，将张力传感器信号接入CH 2，再将分析仪与安装有LMS Test. Lab分析软件的专用计算机连接。运行LMS Test. Lab软件并设置参数。在Channel Setup模块中选择接收信号的 3个通道，并设置张力接口的电压与测试方式，数据采集频率为2 000 Hz。

测试第2.1把梳栉的纱线张力，即间隔丝张力。测试点选在张力杆和梳栉分纱针之间的位置，经编机转速控制在50 r/min，待机器稳定后开始测试，到达采样时间后结束数据采集。最后在Navigator模块中浏览图像或导出测试数据。

2 结果与讨论

2.1 瞬时需纱量和纱线张力的测试结果

导纱针-织针瞬时需纱量测试结果如图3(a)所示，梳栉-织针瞬时需纱量测试结果如图3(b)所示。为方便对比，令瞬时需纱量初始值均为 20.10 mm， 纱线张力的测试结果如图4所示。

图3 瞬时需纱量波动曲线

Fig.3 Instantaneous fluctuation of instantaneous yarn demand.(a) Instantaneous yarn demand of guide bar-knitting needle；(b) Instantaneous yarn demand of guide bar

图4 纱线张力波动曲线

Fig.4 Fluctuation curve of yarn tension

2.2 梳栉摆动对瞬时需纱量和纱线张力影响

表1示出S1的特征状态及参数，表2示出S2与张力F各特征状态及参数，图5示出瞬时需纱量S1特征峰值对应的成圈机件运动状态。

表1S1各特征状态及参数

Tab. 1 Characteristic states and parameters ofS1

特征点转角/(°)机器状态特征值/mm峰值130前针床上升,梳栉后摆24.10谷值160梳栉前移至针床正上方20.10峰值290前针床针前垫纱23.90谷值2120梳栉后移至针床正上方21.50峰值3150前针床脱圈32.70谷值3180梳栉位于针床正上方27.20峰值4210后针床上升,梳栉前摆29.10谷值4240梳栉后摆至针床正上方26.50峰值5270后针床针前垫纱29.90谷值5300梳栉前摆至针床正上方27.20峰值6330后针床脱圈33.80

表2S2与F各特征状态及参数对比

Tab.2 Characteristic states and parameters ofS2andF

特征点转角/(°)机器状态S2/mmF/cN峰值120～30前针床上升,梳栉后摆32.200.200谷值185～95前针床针前垫纱14.000.067峰值2140～150前针床脱圈40.900.196谷值2210～220后针床上升,梳栉前摆20.200.075峰值3265～275后针床针前垫纱38.100.071谷值3325～335后针床脱圈23.900.095

图5 瞬时需纱量特征值的机器状态

Fig.5 State of characteristic value of instantaneous yarn demand

对比表1、2中数据发现，S1和S2有不同的波动频率和强度。S1有6处峰值，各峰值所处的运动状态分别对应图5所示的位置。S2有3处峰值，峰值所处的运动状态分别对应图5(a)、(c)、(e)所示位置，3处谷值所处的运动状态分别对应图5(b)、(d)、(f)所示位置。

为形象描述梳栉摆动对瞬时需纱量波动形态的影响，先对2种曲线的波动强度进行对比分析，重点分析梳栉摆到最后方和最前方的2个动作。图6示出前针床成圈过程(主轴转角0°～180°)中2种曲线S1和S2的波动差异分析图。

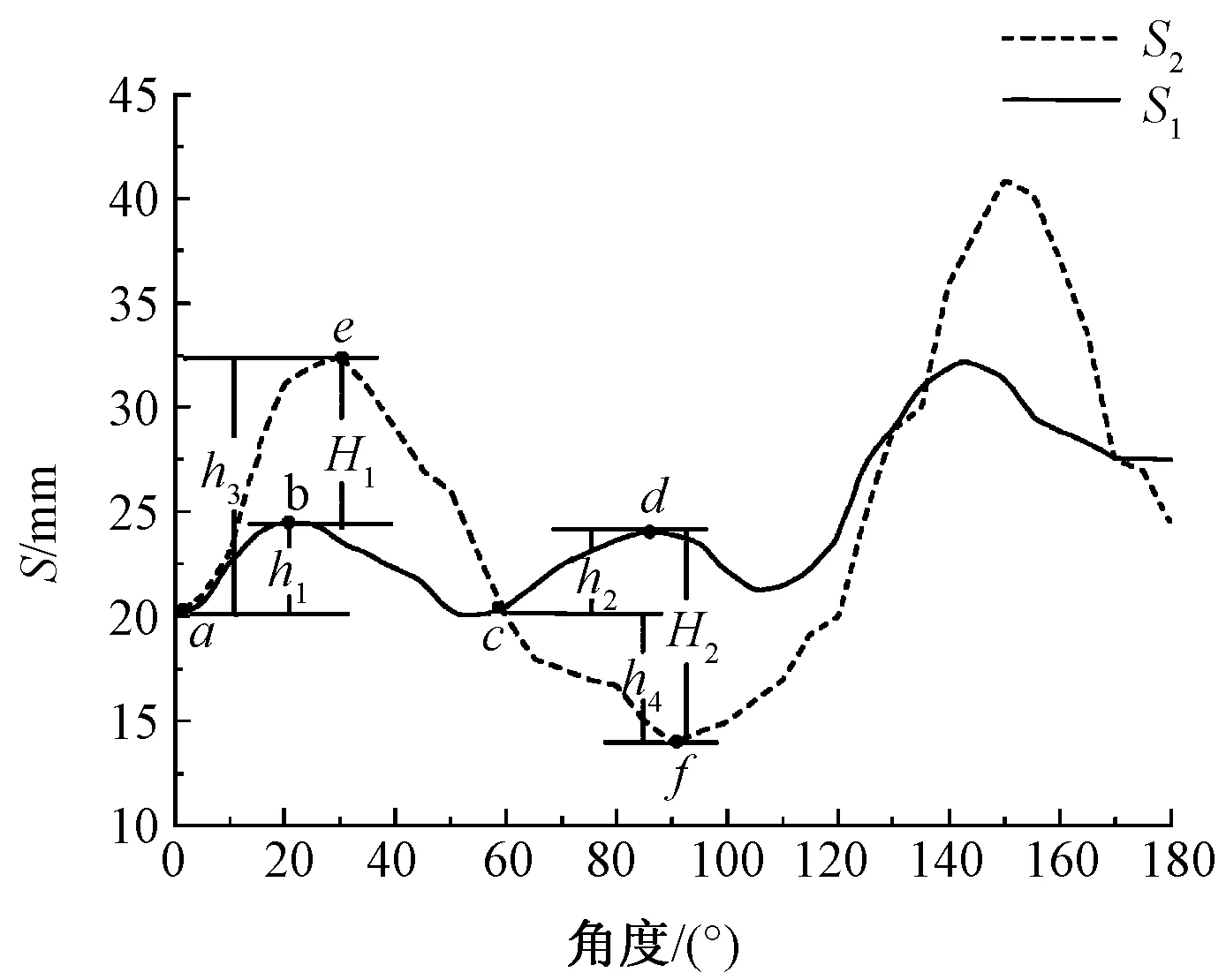
图6 S1和S2波动差异分析图

Fig.6 Difference analysis of fluctuation ofS1andS2

由图6可知：0°～30°梳栉从针床正上方摆到机器后方极限位置，状态如图5(a)所示。此处S1的波动量为h1(30°与0°数值之差)，S2的波动量为h3(30°与0°数值之差)，S2与S1波动量之差为H1为 8.1 mm。60°～90°梳栉从针床正上方摆到机前极限位置，状态如图5(b)所示。此处S1的波动量为h2(90°与60°数值之差，单位为mm)，S2的波动量为h4(90°与60°数值之差，单位为mm)，S2与S1波动量之差为H2为-9.9 mm。为进一步衡量梳栉摆动对瞬时需纱量的影响，需要计算梳栉摆动对瞬时需纱量的影响率，即

式中：p为影响率，%；|S2-S1|为某运动状态时两瞬时需纱量之差，mm。

在30°处梳栉摆到机器后方时，P值为202.5%；90°处梳栉摆到机器最前方，P值为260.5%。这说明：相比于梳栉不摆动的运动形式，梳栉摆到最后方时的瞬时需纱量增加了202.5%，梳栉摆到机器最前方时的瞬时需纱量减少了260.5%，平均变化了231.5%，即梳栉前、后摆动对瞬时需纱量的平均影响率为231.5%。显然可确定，梳栉每次摆动时，梳栉摆动的机器相比于梳栉不摆动机器的需纱波动量增加了2倍以上。

从表2还可看出，纱线张力曲线3个主要波峰的角度范围依次在主轴转角位于10°～30°、120°～140°和250°～270°之间。因为在这3个区间内，梳栉向机后大幅摆动达到极限位置时织针与导纱针之间的距离最大，导纱针与机前后梁之间的距离也是最大，因此，导致从织针到后梁的这段纱线量增大。由于瞬时需纱量大于瞬时送纱量，其差值需要依靠纱线本身弹性伸长和张力补偿装置的变形来补偿，所以纱线张力会突然增大。梳栉前摆时，虽然织针与导纱针的距离也达到最大，但是导纱针与后梁的距离减小，后者减小量大于前者增加量，因此最终的瞬时需纱量表现为谷值。需纱量曲线波动主要受导纱针与织针距离、导纱针与后梁距离差值大小的影响，由此可以推断，梳栉摆动是影响瞬时需纱量和纱线张力波动趋势的最主要因素，而机器速度、花型组织和张力调节方式等也会对瞬时需纱量和纱线张力有影响。

梳栉摆动影响了纱线量的波动，进而影响了纱线张力的波动，因此，纱线张力的变化规律可通过瞬时需纱量的变化规律加以解释，纱线张力曲线和瞬时需纱量S2拥有相似的增区间和减区间。

2.3 从瞬时需纱量到送纱量的推算

由图3(a)可见：180°时前针床成圈完成，导纱针位于织针上方，此时纱线消耗量为27.5 mm。360°(下一个0°)时完成一个横列的编织，此时纱线消耗量为31.4 mm。一个横列消耗的纱线总量为成圈结束时瞬时需纱量与横列初始值之差，即 11.3 mm。如果依此循环，编织480横列时所消耗的纱线量为5 424 mm。从图3(b)可得：成圈结束时瞬时需纱量为31.4 mm，与初始值的差为 11.3 mm，编织480横列所需送经量仍为 5 424 mm/腊克。这说明梳栉的摆动虽然可影响机器总体瞬时需纱量的波动，但不影响导纱针-织针瞬时需纱量，也不影响纱线实际的消耗量。

为验证上述分析的正确性，通过公式对送经量进行理论计算[11]。

式中：m为一个组织循环的横列数；r为机上纵密，横列/cm；R为送经量，mm/腊克。

间隔织物的每个横列包含2个完整的线圈，每个线圈的送经量为

式中：d为织针直径，mm；L为延展线长度，mm。

3 结 论

通过对纱线需求量以及纱线张力值的测试和分析，可以得出以下结论：

1) 除组织工艺外，瞬时需纱量的变化主要受导纱针与织针距离和导纱针与后梁距离差值的影响。梳栉前后摆动改变了这个差值。梳栉每一次摆动导致瞬时需纱量的波动程度增加231.5%，使波动范围增加463%，是影响瞬时需纱量波动最大的因素。

2) 虽然导纱针-织针、梳栉-织针瞬时需纱量2种曲线变化的波动趋势不同，但是成圈结束后所消耗的纱线量是一致的，可以通过计算不同区域瞬时需纱量的差值来分析某个局部区域的送经量，也可以根据需纱量确定合理的送经量和送纱控制方式。

3) 梳栉摆动首先影响了瞬时需纱量的波动，进而导致纱线张力的变化，因此，纱线张力和梳栉瞬时需纱量变化曲线拥有相似的增区间和减区间，而且二者极值出现的角度域也很接近。

FZXB