单轴多级循环加载下聚氯乙烯膜材料的力学行为与能量耗散

汪泽幸， 朱文佳， 何 斌， 刘 超

(湖南工程学院 纺织服装学院， 湖南 湘潭 411104)

膜材料由内部的增强织物和表层面的涂覆高分子材料构成[1]，因内部增强织物微观结构的复杂性、材料与几何非线性及织造与涂层加工过程中经、纬向张力控制的差异，导致膜材料在不同外加荷载下表现出不同的宏观力学行为[2-3]。材料在使用过程中承受如阵风、雨雪的反复作用及预加张力的反复调整等，膜材料通常处于反复加载与卸载状态。此外，膜材料的变形、强度特征及断裂损伤力学特性与所受的应力状态和加载历史密切相关，同时，膜材料在不同应力条件下的破坏实际上是内部微裂纹、缺陷等在荷载条件下断裂、扩张的宏观表现。

目前，众多学者对建筑用膜材料为代表的柔性复合材料在反复加载下的力学行为进行了较为全面的研究：陈务军等[4-7]研究发现聚四氟乙烯膜材料、取偏氟乙烯/聚醚砜膜材料以及机织物增强柔性复合材料的弹性模量、残余变形与反复加卸载次数密切相关；Chen等[8-9]对浮空器膜材料在单、双轴循环下弹性模量的变化趋势进行研究发现，经、纬向应力比与弹性模量之间存在耦合关系，并分析了经、纬向应力比与耦合弹性模量的影响规律；Zhang等[10-12]研究发现，循环加载下PTFE膜材料的单、双轴拉伸行为主要受应力幅值、温度和增强骨架织物结构的影响，且加载历史对力学行为的影响较为明显。

但上述研究主要集中于弹性模量以及拉伸曲线线性程度的变化。而对多级循环加载过程中的能量耗散与演化研究较少。基于此，本文对多级循环加载时的循环加载峰值强度、变形特征、弹性力学性能、断裂损伤力学特性等问题进行研究，对宏观力学行为进行阐述和分析，并对能量耗散及损伤演化进行研究，以期深入了解膜材料的破坏力学行为，为其工程应用提供参考。

1 实验材料与方法

1.1 实验材料

本文以商购涂层法制备的施恩特聚氯乙烯(PVC)膜材料为研究对象，其表层耐气候层涂覆材料为聚偏氟乙烯(PVDF)，增强骨架织物的组织结构为二上二下方平组织，经纱与纬纱均为111.1 tex(192 f)高强涤纶长丝，织物经密和纬密均为24根/(5 cm)，膜材料实测厚度为0.72 mm，面密度为800 g/m2。

1.2 试样制备与实验方法

试样宽度为(50±0.5)mm，长度为(300±0.5)mm，有效夹持隔距为(200±0.5)mm。多级循环加载实验时，以10 mm/min的速率进行自动加卸载，循环峰值应力每级增加5 N/mm，直至试样断裂；为确保实验过程中，试样始终处于张拉状态，卸载下限应力为第一级循环前的预加张力，有效实验样本数为3，对应经向试样编号分别为W-1、W-2与W-3，纬向试样编号为F-1、F-2与F-3。为对比研究多级循环加载时PVC膜材料的强度特性，同时对经纬向试样进行单轴直接拉伸断裂实验，加载速度设定为10 mm/min，有效样本数为5。

所有实验均在室温下采用型号为WDW-20的华龙万能强力试验机进行。

2 结果与分析

2.1 松弛特性分析

PVC膜材料直接拉伸及多级循环加载时的应力-应变曲线如图1、2所示。由图1可知，膜材料经、纬向试样的5次直接拉伸曲线在峰值强度之后应力突然跌落，具有突然破坏的特征。多级循环加载下，应力-应变曲线呈现周期性变化，加载与卸载曲线构成的滞后环面积随着循环次数增加而增加(见图2)。实验结果表明，经向直接拉伸断裂强度为85.88 N/mm，多级循环平均断裂峰值强度为76.67 N/mm，较直接拉伸强度(σC)下降9.21%；纬向单轴拉伸断裂强度为54.78 N/mm，多级循环平均断裂峰值强度为66.67 N/mm，较直接拉伸断裂强度增加21.71%。

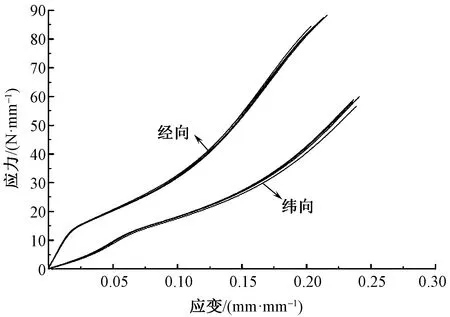
图1 试样拉伸断裂应力-应变曲线

Fig.2 Fracture stress-strain curves of tested specimens

实验用PVC膜材料中增强织物的经密与纬密一致，织造过程中为确保梭口清晰，以便织造加工，经纱所承受的张力较高，伸直度较好。涂层加工过程中，经向亦承受的张力较大，经纱进一步伸直，屈曲程度降低，外加载荷作用下，经纱强力利用率较高，导致膜材料的经向直接拉伸强度较高。

在织造与涂层加工过程中，经纱承受高张力且受反复拉伸、弯曲、摩擦和冲击作用，纤维中大分子已充分伸直；多级循环加载时，大分子之间产生滑移，导致大分子之间作用力下降，宏观表现为多级循环峰值强度低于直接拉伸断裂强度。在织造和涂层过程中，纬纱承受的张力较低且张力波动较小，循环加载作用有利于纤维中大分子的进一步伸直，有利于增强承受外加载荷的作用，从而宏观表现为多级循环峰值强度高于直接拉伸断裂强度。

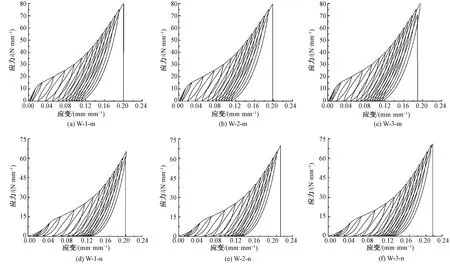
注：m—加载； n—卸载。图2 多级循环加载与卸载下试样的应力-应变曲线

Fig.2 Stress-strain curves of tested specimens under multi-level cyclic loading and unloading

2.2 循环弹性模量分析

循环加载过程中，加载和卸载弹性模量的计算方法主要有线性拟合法和近似等效法2种。线性拟合法：基于加载和卸载应力-应变曲线的初始阶段，对其线性拟合而获得加载和卸载弹性模量，该种方法可反映材料的弹性模量特征；近似等效法：基于初始加载点A与加载终点B连线斜率计算加载弹性模量，基于初始卸载点B(与加载终点同点)与卸载终点C连斜率计算卸载弹性模量，其核心为将加载和卸载曲线近似等效为直线，直线斜率即为加载或卸载弹性模量，此方法计算简便，易于操作(见图3)。

Fig.3 Level 2 stress-strain curves of W-1 specimen

经、纬向试样的多级循环加载与卸载曲线均表现出明显的非线性特征，加载和卸载弹性模量计算时，A、B点间连线斜率高于曲线AB初始段的斜率，同时B、C点连线斜率亦高于曲线BC初始段的斜率。相对于线性拟合法，基于近似等效法计算的加载和卸载弹性模量较高，且无法客观地反映材料的力学行为。

因此，本文基于线性拟合法计算加载和卸载弹性模量，其曲线如图4所示。 可知，PVC膜材料经、纬向试样的加载及卸载弹性随循环加载次数的增加而增加。同一循环内，卸载模量高于加载模量，且随着循环次数的增加，二者之间的差值逐渐增加。

循环加载下，增强纤维和涂层材料中结合力较差的大分子链间产生滑移，并在新的位置建立新的相互结合，且大分子链的伸直程度增加，受力同时性提高，纤维变形主要由大分子链段的伸长和回缩产生，宏观上表现为弹性模量的增加。

2.3 能耗耗散特征

图3中：曲线AB下方区域ABFEA面积为总吸收应变能，表示一个加载与卸载循环过程中外力对试样所做的功；曲线BC下方区域CBFDC面积为该循环的弹性应变能；区域ABCDEA的面积为耗散能，用于试样损伤及塑性变形，总吸收应变能、弹性应变能与耗散能间的关系可表示为：

Ud=U-Ue

(1)

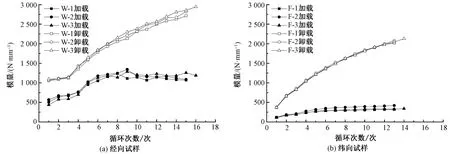
图4 加载与卸载弹性模量曲线

Fig.4 Elastic modulus curves. (a) Warp specimens; (b) Fill specimens

式中：U为总应变能，mJ/mm3；Ue为弹性应变能，mJ/mm3；Ud为耗散能，mJ/mm3。

加载与卸载曲线不重合，形成滞后环，这主要是由于PVC膜材料为典型的黏弹性材料所致；多级循环加载时，材料产生塑性变形，因此，形成的滞后环并未封闭。

试样总吸收应变能、弹性应变能及耗散能的变化趋势如图5所示。可看出，经、纬向试样的能量变化曲线形态相似且呈现非线性增长趋势，表明多级循环加载下经、纬向试样的能量吸收、储存与耗散的机制是一致的。

图5 能量变化与应力和归一化应力关系曲线

Fig.5 Energy variation curves with stress and normalized stress. (a) Total absorption strain energy with stress; (b) Elastic strain energy with stress; (c) Dissipated energy varied with stress; (d)Total absorption strain energy with normalized stress; (e) Elastic strain energy with normalized stress; (f) Dissipated energy varied with normalized stress

同等循环载荷峰值时，经向试样具有较低的总吸收应变能量、弹性应变能和耗散能。以经向试样W-1、纬向试样F-1的第2个加载循环(见图6)为例，因经向试样的加载和卸载模量较高，达到同等循环载荷峰值时，经向试样的初始加载应变(εloading)和卸载应变(εunloading)较小，故加载和卸载曲线下方的面积较小，即总吸收应变能和弹性应变能较小；同时，因同一循环过程中，经向试样产生的塑性形变(εunloading-εloading)也较小，在加、卸载模量差异以及塑性变形差异的双重作用下，经向试样的耗散能也较低。

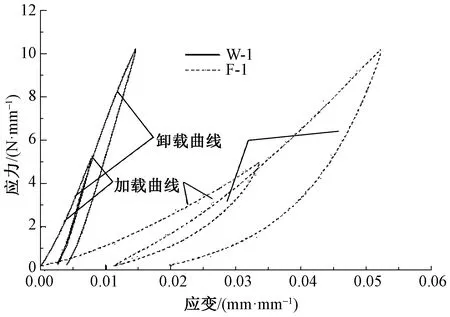
图6 经典试样的第一及二级应力-应变曲线

Fig.6 First and second levels stress-strain curves of typical tested samples

由图5(a)～(c)可知，在同级加载循环中，相对于经向试样，纬向试样的总吸收应变能、弹性应变能和耗散能较高，与纬向试样弹性模量和强度较低的结论不吻合。

图5(d)～(f)示出，同级加载循环对于经、纬向试样是处于不同应力阶段的，就第3加载循环而言，经向试样W-1的峰值应力与纬向试样相差较大，因此同级加载循环的经、纬向试样能量对比不能真实反映材料的能量变化过程，而应力归一化后的分析结果较为可靠。图5(d)～(f)表明：当循环峰值载荷水平较高时，经向试样的总吸收应变能、弹性应变能和耗散能相对较高；而当循环峰值载荷水平较低时，纬向试样的总吸收应变能、弹性应变能和耗散能相对较高。

循环载荷峰值水平较低时，能量的吸收、储存主要依靠增强织物结构的变化、纱线和涂层材料大分子构象的变化来实现；而能量的耗散主要源自增强纤维和涂层材料中大分子链的滑移、原有损伤的扩展、涂层和增强纤维之间结合点的破坏等。因织造和涂层加工过程中张力的差异，相对于经纱，纬纱伸直程度较小且纱线中大分子链段伸展程度不充分，在外加荷载下，纬纱的伸长主要由纬纱屈曲程度减小和大分子链段伸直、滑移构成，纬纱伸长导致模量较低，从而使纬向试样表现出较高的总吸收能；回复阶段，伸直大分子链段向初始状态回复，纱线屈曲状态变化，纬纱屈曲程度较高，对能量的储存能力较强。在循环加载过程中，原有弱损伤得以破坏且因纬纱屈曲结构变化较大，增强纤维与涂层材料之间黏结点破坏概率较高且数量较多，宏观表现为耗散能的增加。

循环载荷峰值水平较高时，能量的吸收、储存和耗散主要依赖增强纤维和涂层材料中大分子链的伸直、回复与滑移。荷载比例越高，大分子链段的伸直程度越高，滑移程度越大，数量越多，同时可回复能力也提高。

2.4 能量耗散率变化规律

将耗散能Ud对总吸收应变能U的比值定义为能量耗散率u，即

(2)

图7示出能量耗散率的变化曲线。可以看出，随着循环载荷峰值的增加，经、纬向试样的能量耗散率呈非线性变化，总体呈现先增加后降低的变化趋势。在加载初期，耗散能Ud占比较低，大部分吸收的能量转化为弹性应变能Ue，表明材料内部缺陷的扩张、增强纤维和涂层材料中大分子链滑移、增强纤维和涂层材料之间脱黏等消耗的能量相对较少，主要转化为可回复的弹性应变能Ue；随着循环荷载峰值增加，耗散能量Ud增加，同时能量耗散率增加，并在循环荷载为20 N/mm时达到极大值；当循环荷载峰值超过此临界值后，虽然耗散能继续增加(见图5)，但大部分能量转化为弹性应变能Ue，能量耗散率呈现逐渐降低的变化趋势。从能量耗散率的角度分析，PVC膜材料使用强度控制在20 N/mm以下较为合理。

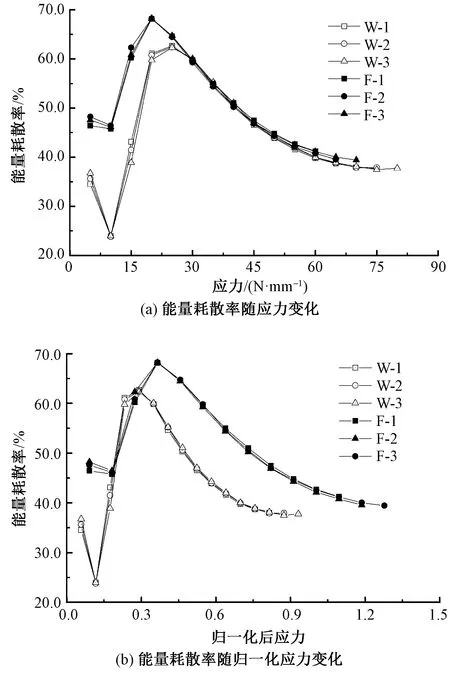
图7 能量耗散率变化曲线

Fig.7 Variation curves of energy dissipation rate withstress (a) and normalized stress (b)

从图7还可以看出，对于第1级循环加卸载过程中，纬向试样的能量耗散率较高，这仍然与织造和涂层加工过程中，经纬向所处的张力状态存在差异有关。

2.5 损伤变量的定义与分析

Lemaitre等[13]从弹性模量变化的角度定义损伤变量，即以弹性模量为损伤因子，认为可利用损伤试样与无损试样的弹性模量之比来定义损伤变量DE，即

DE=1-E′/E

(3)

式中，E、E′分别为无损伤材料与损伤材料的弹性模量，N/mm。

损伤体现为材料缺陷产生、扩展，在此过程中，弹性模量将呈现逐渐降低的变化趋势；当材料完全损伤时，材料发生完全破坏，此时弹性模量E′为0，即材料的损伤变量极限为1.0。

由图5可知，随着多级循环加载的进行，PVC膜材料的弹性模量呈现出递增的变化趋势，故基于弹性模量变化而获得的损伤变量将不可避免出现负值，即材料表现为“负损伤”，计算获得的损伤变量值与实际损伤演化特征相矛盾，所以在多级循环加载条件下，采用弹性模量作为损伤因子的方法是不合理的。

循环加载时，材料可能出现2类破坏极限：1)材料处于弹性工作状态时，循环加载作用下，材料虽不产生塑性变形，但微量损伤在材料结构内部产生、累积，当这些微量损伤累积达到一定程度时，材料达到破坏极限，发生疲劳破坏；2)材料处于弹塑性工作状态时，循环加载将引起材料产生塑性变形并累积，当这些累积塑性变形超过一定程度时，会弱化材料的使用性能，直至出现破坏极限。

从能量转换的角度而言，损伤的累积意味着能量的耗散，因而可从能量耗散的角度定义损伤变量，故可将各循环加载过程中累积的耗散能与最后一级加载循环的总应变能比值定义为损伤变量DU，即循环加载到第i级时损伤变量DU(i)可表示为：

(4)

式中，U(t)为最后一级循环的总应变能，mJ/mm3。

基于式(4)计算而得的损伤变量与循环级数之间的关系见图8。可以看出，循环加载次数约超过7次后，经、纬向试样损伤变量值均大于1.0，与损伤极限为1.0矛盾，故采用式(4)计算损伤变量也不适用。

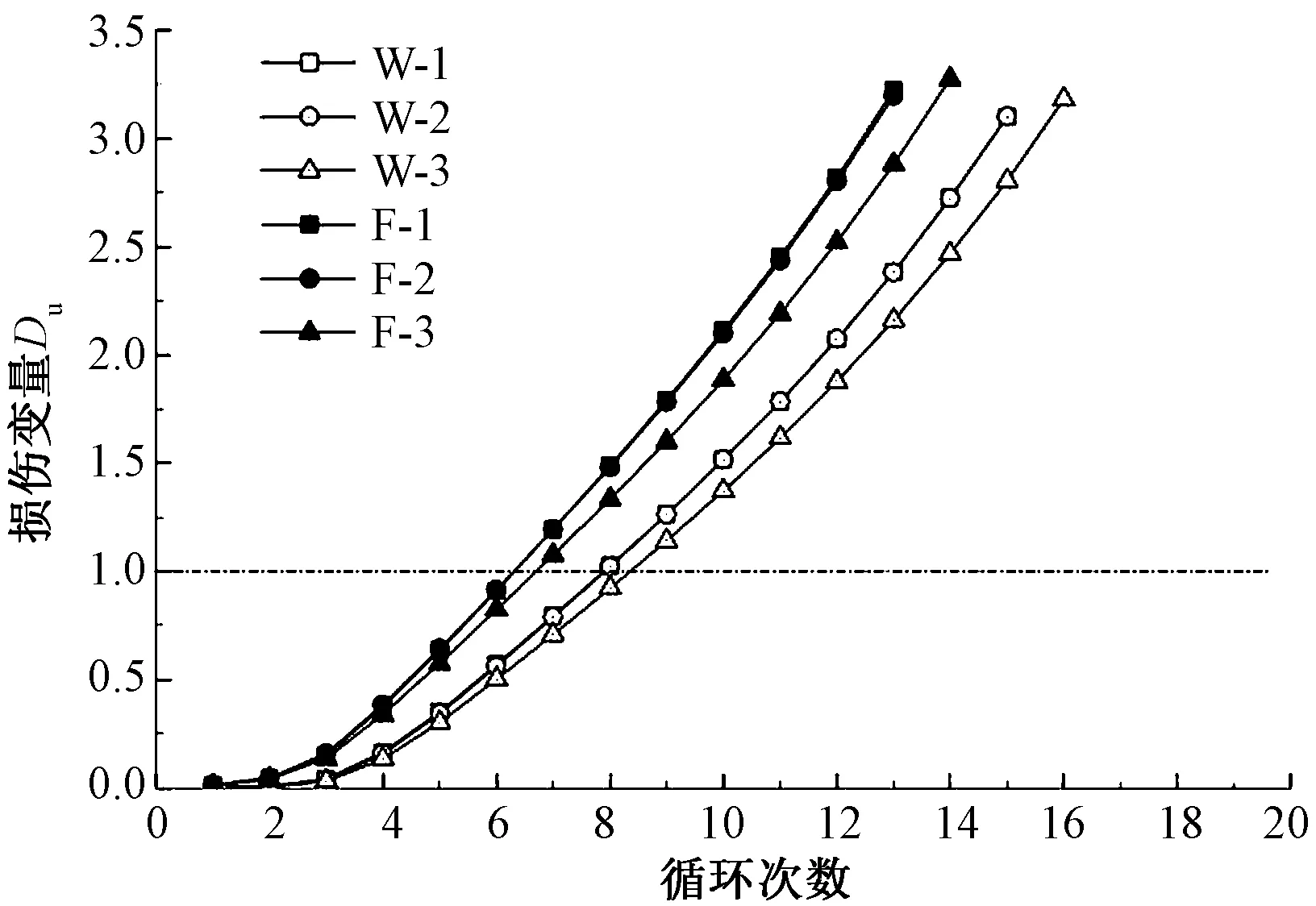
图8 损伤变量DU与循环次数曲线

Fig.8 Curves of damage variableDUand cycle number

由图2、3和6可知，PVC膜材料的加载和卸载曲线并不重合且构成的滞后环也不封闭，从而表明在整个多级循环加载过程中，PVC膜材料均处于弹塑性工作状态，循环加载将引起塑性变形的累积，从而导致材料性能的劣化，基于此，可定义损伤变量为各加载循环累积的塑性应变与无损试样(直接拉伸试样)断裂应变之比，即加载到第i级循环时损伤变量Dε(i)可表示为：

(5)

式中：εb为单向拉伸时试样的断裂应变，mm/mm；εper为各循环产生的塑性变形，mm/mm。

基于式(5)计算而得的损伤变量Dε与循环加载次数之间的变化关系如图9所示。

图9 损伤变量Dε与循环次数曲线

Fig.9 Curves of Damage variableDεand cycle number

从图中可以看出，基于塑性变形累积而计算获得的损伤变量Dε值在0～1之间，在损伤极限范围之内可认为，基于塑性变形累积来定义损伤变量较为合理；同时发现，在随着多级循环加载的进行，经、纬向试样的损伤均呈现相似的非线性增长趋势，表明PVC膜材料经、纬向的损伤机制相似，且同等循环荷载峰值条件下，纬向试样的损伤程度高于经向试样。

3 结 论

本文对PVC膜材料在单轴加载下的多级循环和直接拉伸性能进行了测试和分析，研究了多级循环加载下PVC膜材料的变形行为及机制，分析了PVC膜材料在多级循环加载下的损伤特性，实验分析结果如下。

1)本文选用的PVC膜材料，其经向试样的多级循环断裂峰值强度低于直接拉伸强度，而纬向试样高于直接拉伸强度，这主要因为织造和涂层加工过程中经纬向纱线所承受的张力差异。

2)因PVC膜材料的加载和卸载曲线呈现明显的非线性，因而相对于近似等效计算方法，采用线性拟合法来获取加卸载模量较为合理。随多级循环加载的进行，加载和卸载弹性模量总体表现出递增的变化趋势，且卸载弹性模量高于加载弹性模量。

3)由于多级循环加载的峰值强度与循环加卸载次数不同，经、纬向试样在相同循环加载次数时，其各自的变形过程处于不同阶段。能量与归一化应力变化趋势表明，小载荷水平下，相对于经向试样，纬向试样的总吸收应变能、弹性应变能和耗散能较高，但在高载荷水平下较低。

4)多级循环加载时，PVC膜材处于弹塑性变形阶段，相对于基于弹性模量变化和耗散能累积定义损伤变量，基于塑性变形累积来定义损伤变量较为合理。

FZXB