基于GHM多小波变换的非织造布多焦面图像融合

陈 阳， 辛斌杰， 邓 娜

(1. 上海工程技术大学 电子电气工程学院， 上海 201620； 2. 上海工程技术大学 服装学院， 上海 201620)

非织造布是由纤维随机或定向排列而成，生产以纺黏法为主。非织造布的性能与纤维网的孔隙构造紧密相关，而纤维的厚度、宽度、取向度以及纤维网的形成方式等都与其构造有关，因此能够得到这些结构参数进而找到性能间的联系，对生产及用途都具有十分重要的指导意义。目前主要使用间接法对非织造布孔隙结构进行解析，而其存在的问题集中在费时费力且不能考虑到孔结构的复杂性。计算机数字图像处理技术的发展为研究非织造布结构和性能提供了有效工具。图像质量对纤维的形态测量与结构解析至关重要。

非织造布的厚度太大使得一般光学显微镜的景深不足以将所有纤维清晰地显现在一幅图像中。基于这种不完全聚焦图像的测量，纤维结构将是不准确的，甚至会对后续处理有一定的误导性[1]。由此，在该情况下引入多焦面图像融合的概念[2]。多焦面图像融合可以说是图像融合的一个研究部分[3-4]。多焦面图像融合旨在使用融合技术将同一场景的不同焦点拍摄的2个或多个图像，来形成具有均匀焦点和清晰内容的另一幅清晰图像[5]。针对多源图像，很多算法被研究出来，如小波变换算法[6]；基于金字塔的融合算法：FSD[7-8]、对比度[9]、拉普拉斯(LAP)[10]；平移不变离散小波变换(SIDWT)图像融合算法[11]和空间频率融合算法[12-13]等。目前这些算法仍然被用来处理相应的图像融合。最近，一些基于变换技术如离散余弦变换(DCT)[14]、非下采样轮廓波变换(NSCT)[15]，基于区域的融合算法[16-18]也被用于研究多焦面图像融合中。

本文使用的是基于多小波的多焦面融合技术，很好地解决了单小波只适用2幅图像的局限性[19-20]。Mallat快速算法通常运用于以小波算法为基础的图像融合方法中[21]，能够有针对性地对需要保留的信息进行提取，对边缘保持度、信息量有所保证，从而融合效果与基于金字塔形变换的算法相比更加好。这是因为小波变换更为紧凑。重点在于将高频和低频使用2种方法进行融合操作。主要步骤是将采集到的前2幅图依照多小波变换融合形成图像，接着和下一幅单焦面图像再按照该方法融合，不断迭代，从而得到最清晰的图像。

1 图像采集

用于非织造布分析的计算机辅助显微镜系统是由1台三目显微镜、1台数码相机(PDS50)和1台三轴机动平台组成，如图1所示。三轴载物台在x，y方向上传送样品载玻片，并在每个(x，y)位置调整图像在Z轴上的焦点从而来捕获不同的焦平面，形成一系列的单焦面图像。

图1 图像采集装置

Fig.1 Image acquisition device

从非织造布上切下1 cm×1 cm的测试样品，然后将其放置于载玻片上，并利用显微镜进行成像。根据实际样品的厚度在不同焦平面或层处捕获20张左右图像。每个捕获的图像均具有2 592像素×1 944 像素的尺寸。图2示出样品的20个多焦面图像中的9幅图像。发现在不同的聚焦平面上，每个纤维的清晰度是不同的。

2 多小波变换原理

2.1 图像滤波

多小波分解的是一个矢量信号。在分解图像前需进行预处理，而预处理主要是预滤波。过采样和预滤波后的数据量将呈指数增长，这不适用于本文中的多焦面滤波。本文采用临界采样预滤波，与一般的自适应滤波器相比，其对减少运算繁琐度并提升整体收敛速率很有用。

如果M×N的标量源图像被预先滤波，则获得大小为(M×N)/r2的多个图像输出。预滤波后经小波分解及逆变换得到初始融合图像。

2.2 GHM多小波变换

GHM多小波和其他多小波都有以下特点：在合理的平移后，多小波是对称的，能够使滤波器具有线性或广义线性相位，规避了重组造成的偏差；它的每个缩放函数都是短支撑的，可以避免由于截断导致的错误，因此适合处理边界问题；一阶消失矩存在于全部小波中，为了在应用操作中能够高效重组，就需要一个二阶消失矩;正交性在应用中对偶是其本身，由于不需要构造函数，减少了很多操作[22]。单小波及其尺度函数不足以共同拥有这些性质，所以单小波不便于应用。多小波能够同时具备这些特性，这比单小波更适于应用，得到成果也更快速、精准。

图2 在不同焦平面捕获的非织造布样品图像

Fig.2 Nonwoven fabric sample images captured at different focal planes.(a)Image 1;(b) Image 2; (c) Image 3; (d) Image 4; (e) Image 5; (f) Image 6; (g) Image 7; (h) Image 8; (i) Image 9

多小波是由r≥2个尺度函数Φi(t)和相应的小波函数Φi(t)构成，若有Φ(t)=[Φ0(t),Φ1(t),∧,Φr-1(t)]T,Ψ(t)=[φ0(t),φ1(t),∧,φr-1(t)]T，那Φ(t)与Ψ(t)符合二尺度方程：

式中:Φ(t)=[Φ1(t),Φ2(t),…,Φx(t)]T为尺度函数向量；Ψ(t)=[Ψ1(t),Ψ2(t),…,ΨN(t)]T为小波函数向量；Hk为N×N的尺度；Gk为小波滤波器矩阵(N≥2)。

3 非织造布多焦面融合

本文使用多小波来实现多焦面图像融合。融合原理依据非冗余和方向特征来实现。多小波分解可以使图像分层为2种频带的特征分量。高频拥有细节和丰富的轮廓数据，而低频通常反映图像的大规模特性，因此，选择不同的融合方法来处理来自高低频带的子图像。将小波得到的20几个单焦面图像中的2个分解后，应用不同的高频和低频融合规则，然后将融合图像1小波逆变换。接着再使用融合图像1和其他单焦面图像继续融合，直到纤维清晰地显示在融合图像中。具体流程图如图3所示。

图3 多焦面融合算法流程图

Fig.3 Multi-focus image fusion algorithm flow chart

3.1 高频系数处理规则

高频部分运用基于区域能量方向性的加权融合规则，选取能量绝对值较大的作为高频信息运用到后续处理。区域能量融合规则的使用与传统规则相比，能够更好地提高处理图像的亮度，更好地提取原图信息，切实提高融合质量。

其使用的高频融合规则为：

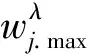
3.2 低频系数处理规则

低频部分表示图像中亮度或灰度值改变较平缓的区域，即图像中占比较大的平缓区域，并描述图中的主要部分。本文使用基于层间相关性的区域方差的方法处理低频系数。该方法能够依据系数查找到有用信息在目标子图像中的方位，因为在小波分解后图像细节会出现在相近的方位。

其中低频融合规则为：

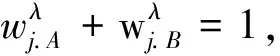
3.3 非织造布多焦面融合步骤

1) 对源图像进行r×r阶预滤波处理，运用临界采样，将其达到图像标量信息转化为矢量信号的效果。

2) GHM多小波分解:将采集到的第1幅(A)及第2幅(B)单焦面源图进行分解，分别得到A、B的高、低频分量系数。

3) 高频分量使用基于区域的方向性和能量加权融合方法，并选取区域匹配度来选择较大区域能量作为融合图像结果。

4) 低频分量采用基于层间相关性的区域方差融合方法，选择相关性大、变化均匀、离散度小的区域作为最终融合图像。

5) 高频和低频分量系数进行逆运算，重构获得初始融合图像。

6) 得到的初始融合图像再作为A，第3幅图再作为B，依次再进行上述步骤直至所有纤维清晰呈现在最后的融合图像中，即可停止。

3.4 非织造布多焦面融合效果图

多小波算法在非织造布的多焦面融合中起到了不错的效果。一般而言，人眼容易识别出融合前后的差别。下面从不同的融合算法效果图及不同的非织造布样品效果图中验证多小波算法的鲁棒性。

3.4.1 各种融合方法比对

图4示出同一样品的融合效果来对比6种算法的差异，为更直观看出本文算法的优越性，将融合图像局部放大。可以看出梯度金字塔及单小波效果最差，其次是双小波，梯度金字塔及拉普拉斯金字塔融合的图像边缘很清晰，但仍有小部分纤维边缘较模糊，最好的是本文使用的多小波，所有纤维均清晰显示。客观评价可以从下文图像质量评估中得到本算法效果是最好的。

图4 各方法多焦面融合效果图

Fig.4 Multi-focus image fusion effect of each method. (a)Multi-wavelet;(b)Single wavelet;(c)Double wavelet;(d)Partial enlargement of multi-wavelet;(e)Partial enlargement of single wavelet;(f)Partial enlargement of double wavelet;(g)Contrast pyramid;(h)Laplacian pyramid;(i)Gradient pyramid;(j)Partial enlargement of contranst pyramid;(k)Partical enlargement of laplacian pyramid;(l)Partical enlargement of gradient pyramid

3.4.2 多小波方法用于不同非织造布样品

本文使用的多小波算法应用范围广，适用于不同的非织造布样品。本文在图5中列举了6种非织造布，分别为样品1#(丙纶与涤纶的混合，25 g)、样品2#(涤纶，30 g)、样品3#(丙纶，30 g)、样品4#(抗老化产品，30 g)、样品5#(阻燃产品，30 g)、样品6#(丙纶与涤纶的混合，27 g),通过对比原图与融合后的图像，可以很清晰地看出本文算法的优越性，所有纤维均清晰显示，为后续的纤维直径、孔隙率及取向度测量提供基础。

图5 6种样品的原图及融合效果图对比

Fig.5 Comparison of original and fusion effect diagrams of 6 kinds of samples. (a) 1#; (b) 2#; (c) 3#; (d) 1#after fusion; (e) 2#after fusion;(f) 3#after fusion; (g) 4#; (h) 5#; (i) 6#; (j) 4#after fusion; (k) 5#after fusion; (l) 6#after fusion

3.5 融合图像质量评估

图像融合质量评价是客观的，是测试图像处理系统性能好坏的重要依据。主观评价凭感知者的主观感受，但受环境影响较大，而客观评价则处于研究热点。本文使用5种技术参数从多方面评价融合的优劣，其定义如下。

3.5.1 平均信息熵

信息熵是图像包含平均信息量大小的度量。融合图像的熵越大，说明图像中的信息量越多，融合的效果越好，平均信息熵即其平均值。平均信息熵定义为：

式中：p(i)为图像取灰度值的概率，可近似为灰度的频率；L为灰度级数。

3.5.2 平均梯度

平均梯度即灰度变化率，这种变化率的大小可用来表示图像清晰度。平均梯度越大，图像层次越多，也就越清晰。平均梯度定义为：

式中:R、C为图像长、宽；I(i,j)为(i,j)位置的灰度值。

3.5.3 互信息

表示2个变量X与Y是否有关系，以及关系的强弱。互信息定义为：

式中：X、Y为原始图像和融合图像；P(X,Y)为联合分布概率。

3.5.4 均方根误差

均方根误差是用来衡量观测值同真值之间的偏差。本文算法的均方根误差为：

3.5.5 峰值信噪比

峰值信噪比越高，说明融合效果和质量越好。峰值信噪比定义为：

根据上述5种图像质量评价指标，将各方法的融合图像进行对比，结果如表1所示。

表1 融合图像质量评估表

Tab.1 Fusion image quality assessment form

类型H-gMIMMSEPSNR多小波变换6.618 68.011 70.532 244.755 031.876 0加权平均6.458 51.783 40.861 548.865 331.843 8单小波变换6.367 74.751 70.787 852.281 531.198 0双小波变换6.336 37.954 30.681 555.529 730.771 0拉普拉斯金字塔融合5.632 17.926 50.543 858.908 430.757 1对比度金字塔融合4.409 87.944 30.564 579.210 329.284 4梯度金字塔融合6.862 63.778 20.629 457.966 030.511 0

从表1可以看出，本文方法得到的融合图像的互信息最小，平均梯度最高，平均信息熵第二高，均方根误差最小，峰值信噪比最高。从这些数据可以看出本文方法融合得到的图像边缘保持度高，信息丢失少，并且得到的信息量多，且清晰度也最高，融合效果和质量也最高，由此也证明本文方法切实可行，效果好。

4 结 论

本文提出使用多小波融合算法进行非织造布多焦面融合，针对不同分量不同频率特性的特点，采用2种融合规则，更好地进行多焦面图像融合。融合的图像结合了多焦面图像的选择特征，使得未聚焦的光纤可被实际地修正，并且模糊纤维边缘可被锐化。与单焦点图像测量的数据相比，从融合图像中获取的数据可大大提高纤维厚度测量的准确性。其次，本文使用的方法能够对显微镜得到的图像直接融合，不需要进行预处理，且融合时间相对而言较短，使得融合更加高效。当然，本文的非织造布多焦面融合只是研究的第1步，本文的侧重点在于多焦面融合,并且不久之后将会在图像融合的基础上对非织造布形态与结构进行解析与测量。

FZXB