碳纤维织物在热流冲击下的热传递数值模拟

郑振荣， 智 伟， 韩晨晨， 赵晓明， 裴晓园

(1. 天津工业大学 纺织科学与工程学院， 天津 300387；2. 天津工业大学 先进纺织复合材料教育部重点实验室， 天津 300387)

流体与固体表面之间热量传递的现象为对流传热，对流传热主要依靠流体质点的运动传递热量，与流体的流动情况密切相关。对流加热在工业中常用于材料的热风干燥过程和金属锻造过程中，能达到快速干燥和加热的目的。对流加热也会产生高温热伤害，如航天上高超声速飞行器在服役过程中表面与周围气流发生强对流传热现象，使固体表面温度急剧升高，高温使飞行器整体结构刚度下降，破坏材料抵抗变形的能力，受热严重部位易产生热应力、热应变等现象，导致飞行器不能安全稳定飞行；工业上高铁及动车在高速运行时其车头与周围气体产生强对流传热现象使车头表面的温度升高，导致高铁及动车车头结构和材料受损；消防员在外界环境中因风速的存在会受到高温热流的正面侵袭，对消防员身体构成严重的伤害。为减少甚至消除高温热流带来的热伤害，研究热流作用下织物的传热机制和传热过程成为关键。目前人们在研究材料高速热流或气流环境下的防护性能时，大都是通过风洞试验及飞行试验等来研究材料的热力学性能，设备复杂，影响因素多且不易控制[1]，周期长，成本高，具有不可重复性。

以传热学基本理论为基础，以计算机软件为工具，利用数值模拟的方法预测材料的传热性能具有简单、快捷、成本低、节约资源等优点[2]。Kamran等[3]使用有限体积法建立多层纤维材料辐射-传导传热模型，并分析轻质多层纤维材料在高温热流条件下的热传递特性；Ji等[4]在高温热流条件下，建立高温多层绝缘结构的二维数值模型，基于辐射-传导机制利用有限元法求解高温下多层绝缘材料的温度分布，模拟结果与实验结果吻合良好，其中耐高温多层绝缘结构由多层纤维绝缘材料和金属箔组成，计算时将多层纤维绝缘材料当作匀质板材；樊钰等[5]在高温热流条件下采用一维瞬态传热理论数值模拟固体火箭发动机碳纤维/环氧树脂复合材料壳体的温度场分布，并利用风洞试验验证模型的准确性，所得温度场分布与试验结果吻合较好，模拟时把复合材料壳体简化为平板进行计算；李旭东等[6]介绍了一种金星进入飞行器，该结构外部采用柔性碳纤维织物与辐条连接，建立半刚性机械展开式结构的模型，利用数值仿真方法预测柔性织物表面在不同速度下的热流密度，建立模型时把柔性织物当成匀质材料考虑。

综上所述，虽然人们在利用数值方法预测热流作用下纺织材料的传热性能方面已经取得了很大进展，但往往忽视纺织材料的组织结构参数对其传热性能有重要影响。多数纺织材料是纱线和空气组成的多孔材料，其孔隙率在60%～80%[7]，显然利用数值方法研究材料的传热性能时，将纺织材料看作匀质平板是不合理的。

碳纤维纺织材料热力学性能优异，具有高强、高模量、密度小、质量轻、耐摩擦、尺寸稳定性好等特点，是理想的功能和结构材料[8]；在热学性能方面，碳纤维具有较高熔点，较大的比热容，良好的耐高温特性[9]，因此碳纤维材料在航空、军用和工业领域有广泛的应用前景。本文以碳纤维平纹织物为研究对象，基于纱线的横截面形状和交织路径函数，建立碳纤维平纹织物的三维几何模型；在此基础上根据热环境利用传热学基本理论建立热流作用下织物热传递过程的数值模型，预测织物厚度方向温度变化情况，并自行设计搭建试验平台验证该传热数值模型的准确性。

1 织物三维几何模型的建立

1.1 模型参数的获取

本文采用日本东丽T700 12 K型碳纤维纱，织物经纬密为26根/(10 cm)× 24根/(10 cm)。建立织物几何模型前，需要准确获得织物的经纬纱线交织路径函数、经纬纱截面形状、尺寸等参数。本文选用的碳纤维纱较粗，上机织造时经纬纱较稀疏，经纬密小，利用Xradia 510 Versa型三维X射线显微镜(德国卡尔·蔡司股份公司)观察织物中的纱线形貌；由于织物中的碳纤维纱为丝束，易脱散，采用火棉胶溶液对织物进行处理，使之在织物表面形成一层保护膜，起固定作用[10]。在电镜图片上利用ImageJ软件测得经纱宽度为3.48 mm，纬纱宽度为3.02 mm，经纱高度为0.29 mm，纬纱高度为0.32 mm，经纱间距为3.97 mm，纬纱间距为3.15 mm。

采用YG141LA型数字式织物厚度仪(莱州电子仪器有限公司)根据ASTMD1777标准测试碳纤维平纹机织物的厚度，测试标准压力为 600 cN，压脚面积为2 000 mm2(Φ50.48 mm)，测试10个点并取平均值，测得织物厚度为0.67 mm。

1.2 模型的建立

图1 碳纤维织物

Fig.1 Carbon fiber fabric.(a)SEM of fabric;(b)Geometry model of fabric; (c) SEM and geometry model of warp cross-section;(d) SEM and geometry model of weft yarn cross-section

利用诺丁汉大学开发的商业建模软件Texgen[11]建立碳纤维平纹织物的三维几何模型。建模过程中根据电镜图中纱线截面形状对纱线横截面模型进行局部修改，定义纱线路径上各个节点的空间坐标，采用样条曲线获得纱线交织路径，避免纱线屈曲处出现重叠、凹陷[12]，构建出碳纤维平纹织物的三维几何模型。图1示出碳纤维织物的电镜照片与三维几何模型图。由图1(a)、(b)可见，织物三维模型能够准确反映织物的几何结构情况；由图1(c)、(d)可看出经纬纱线的横截面均为椭圆形，模型中经纬纱横截面与电镜图片有较好的一致性，且平纹织物结构较均匀，纱线之间无重叠。

2 碳纤维织物热传递性能的数值模拟

2.1 热传递理论

为探讨碳纤维织物在热流冲击下的传热机制，将尺寸为30 cm×20 cm的碳纤维织物竖直放置(见图2)，用一束热气流垂直冲击织物的正面中心位置，假设热流冲击面积小于织物，织物背面初始条件为17 ℃室温环境。

热流冲击到织物表面后，假定织物致密，纱线间孔隙内为静止空气，不考虑气流通过织物孔隙的对流。此时碳纤维织物在热流冲击下的传热过程为：首先对流换热使织物表面温度升高；其次织物表面通过热传导传递到织物背面；然后织物和外界发生辐射和对流换热。碳纤维织物在对流热冲击下，其传热途径包括热传导、热对流、热辐射，热量传递过程中各个环节的换热方式如图2所示。

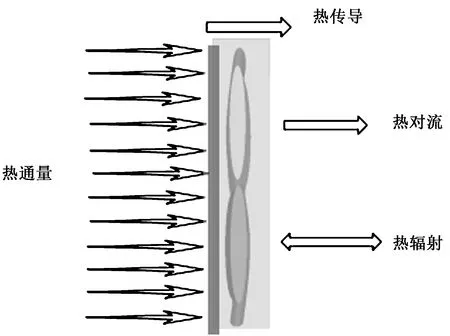
图2 碳纤维织物在对流热冲击下的热量传递机制

Fig.2 Principle of heat transfer with carban fiber fabric under heat flux

1)传热微分方程的建立。当材料仅受到传导热且无内热源时，假设热量仅在材料的厚度方向进行传递，其一维导热微分方程[13]为：

(1)

式中：ρ为材料密度，kg/m3；c为比热容，J/(kg·℃)；λ为导热系数，W/(m·K)；T为温度，℃；t为时间， s。

在热流冲击下织物背面温度升高后可以通过对流向环境散热，根据牛顿冷却公式[14]

Qc=hPdx(Tw-TF)

(2)

式中：h对流传热系数，W/(m2·K)；Tw固体表面温度，℃；Tf为流体的温度，℃；P为截面周长，m。

织物温度升高后与外界发生辐射热交换，根据斯蒂芬-玻耳兹曼定律，物体辐射热流量

(3)

式中：Ten为周围环境的温度，℃；ε为物体的发射率,%；σ为玻尔兹曼常数，为5.67×10-8W/(m2·K4)。

再根据能量守恒可知：

Qe=φq-ΔQx-Qc-Qr

(4)

式中：Qe为单位时间内微元体内能的增量，W/m2;φq为织物正面获得的热通量,W/m2；ΔQx为x方向的导热流量,W/m2；Qr和Qc分别为辐射散热和织物背面的对流散热，W/m2; 整理可得式(5)，其中φx为织物正面获得的热流密度,W/m2。

因此可得出在热流作用下，碳纤维织物的一维传热微分方程为：

(5)

2)瞬态传热系统。热分析包括稳态热分析和瞬态热分析，在初始温度已知的条件下，利用瞬态热分析来实时检测温度场随时间的分布情况。分析过程遵循方程：

[C]{T}+[K]{T}={Q}

(6)

式中:[K]为传导矩阵，含导热系数、对流传热系数；[C]为比热矩阵，包括系统内能的增加；[T]为节点温度向量；[Q]为节点热流向量。

2.2 材料属性

将织物三维几何模型导入到有限元软件后，利用布尔操作创建经纬纱线与空气的联接，使织物模型系统装配为纱线和空气的集合体，并赋予纱线与空气一系列属性参数。所需纱线和空气的属性参数包括纱线的密度、导热系数、定压比热容。空气属性参数可根据不同的环境温度查表得到[15]。纱线的密度采用比重瓶法测量；纱线的导热系数和定压比热容采用基于瞬变平面热源技术的Hot Disk热常数分析仪测量。表1示出碳纤维纱线和空气的热物性参数值。

表1 材料的热物性参数

Tab.1 Thermophysical parameters of materials

材料质量密度/(kg·m-3)导热系数/(W·m-1·K-1)定压比热容/(J·kg-1·K-1)空气 1.060.0291 005碳纤纱1 798.900.5281 318

2.3 网格划分

在有限元软件中，采用映射网格中的四面体网格类型对织物模型进行划分网格[16]，单元尺寸为1.5×10-4mm。再通过相关性水平来调整网格的疏密程度，根据实际情况选择50。通常网格越精细，数值模拟求解的精确度越高。织物模型划分的单元数量为268 547，节点数量为402 536。

图3 碳纤维织物模型网格划分

Fig.3 Meshed of carbon fiber fabric model.(a)Fabric mesh model;(b)Air domain mesh

2.4 边界条件

为简化计算，将织物内部的热量传递过程看作沿织物厚度方向上的一维瞬态传递过程。假设组成织物的经纬纱是各向同性材料，且经纬纱线热物性恒定，织物边界与外部环境无热量交换；在模拟计算中，对织物受热面施加恒定的热流密度值为 1 319 W/m2。热对流和热辐射载荷施加在织物外表面，如图4、5所示。经计算织物外表面的对流传热系数为25 W/(m2·℃)，采用TIR100-2型红外热发射仪测定织物的辐射率为0.5。时间步长为4 s，计算80 s内织物的温度分布情况。

图4 对流载荷

Fig.4 Convective load

图5 辐射热载荷

Fig.5 Radiation load

3 试验验证

为研究在一定热流冲击下碳纤维的传热性能，自行搭建了对流热冲击下纺织品传热性能的测试平台，其示意图如图6所示。

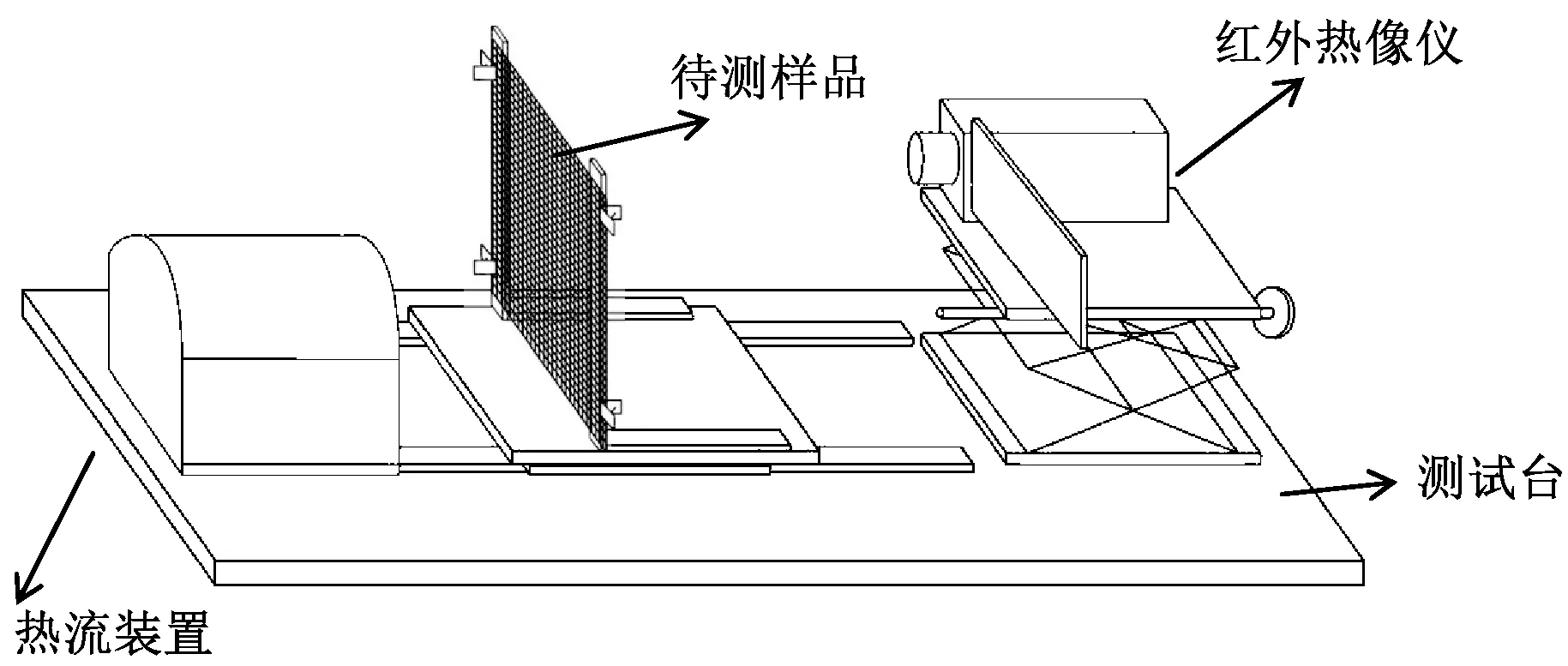
图6 验证试验示意图

Fig.6 Schematic diagram of verified experiment

该测试平台包括热流发生装置、样品架、Green TEG热流计、数字风速仪、红外热像仪。待测织物的尺寸为30 cm×20 cm。气流出口速度可用数字式风速仪测定，测试方法为将风速计打开并调零，多次测量气流出口的速度，保证其为稳定状态。

织物表面的热流密度值可通过接触式热流计Green TEG测得，其工作原理是利用热流传感器接收热流信号，并产生与热流成正比的输出电压，热流值即为该输出电压除以传感器灵敏度的值，最后在电脑终端显示[17]。每个热流传感器均有其各自的灵敏度。具体操作是选择一个热流计探头，利用导热贴将探头正对着热气流出口处固定在待测织物表面，然后打开软件TracerDAQ记录对应探头下的数据，多次测量求其平均值。

红外热像仪的工作原理就是测量物体发出的不可见红外能量转变为可见的热图像。热图像的不同颜色代表被测物体的不同温度。红外热像仪是一种二维的、非接触式的测温设备。它具有测温范围广、测试结果精确等优点。本文试验利用红外热像仪测试织物背面的温度云图，获得热量在织物样品厚度方向上的传递过程。

4 结果与分析

4.1 数值模拟结果与分析

利用有限元方法对碳纤维织物在对流热作用下的传热方程进行计算求解后，可获得织物在热流冲击各时间节点处的温度分布云图，同时还可自动生成温度随时间变化的动态云图，并能得到在织物背面选中的某个节点随时间变化一系列温度值，预测在热流作用下碳纤维织物背面温度随时间的变化规律。图7、8示出碳纤维织物受热流冲击8、24、48、80 s时模型厚度方向和纱线的温度分布云图。

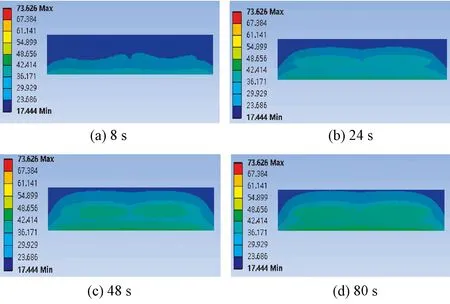
图7 织物模型厚度方向温度分布

Fig.7 Temperature distribution in thickness direction of fabric model

图8 织物模型中纱线的温度分布

Fig.8 Yarn temperature distribution in fabric model

从图7、8可见，织物受热面随着热流冲击时间的延长，织物背面的温度逐渐升高，热量主要沿织物厚度方向传递，在55 s后传热过程达到平衡，织物背面温度逐渐稳定在46 ℃左右。在织物水平方向上，碳纤维平纹织物较稀疏，因气流的作用，织物中的空气由静止变为流动状态，流动空气的热传导能力大于静止空气热传导能力，使得孔隙处纱线温度升高较快；织物中经纬纱线按照一定方式上下交织，使纱线呈现高低不平的起伏状态[18]，当织物底部与热气流接触时，弯曲程度较高的部分首先接触热流，温度较高。

4.2 热流冲击下织物传热计算结果的验证

对碳纤维平纹织物受热面施加热流密度值为 1 319 W/m2的载荷时，利用建立的热流冲击下织物热传递数值模型可得到织物背面温度随时间变化情况。在织物背面随机选取1个节点，求得传热80 s内该节点随时间变化的温度值，并将其与试验值进行比较，如图9(a)所示。另外其他条件不变，改变待测织物受热面所受到的热流密度为1 103 W/m2，计算求得待测织物传热80 s内的温度分布，与试验所测织物背面温度曲线对比，如图9(b)所示。

Fig.9 Temperature distribution on back of fabric

从图9可见，碳纤维织物背面温度随受热时间延长逐渐增加，前30 s内上升较快，55 s左右织物背面温度趋于稳定。当热流密度为1 319 W/m2时，达到传热平衡时织物背面温度为46.16 ℃，模拟值为46.11 ℃，二者结果相似度较高，其背面温度的模拟值和实验值平均误差为6.64%；当热流密度为 1 103 W/m2时，传热平衡时织物背面温度为 37.85 ℃，模拟值为38.87 ℃，二者结果相差不大，经计算背面温度的模拟值和实验值平均误差为3.28%，这说明该模型能较好地反映碳纤维平纹织物的动态传热过程。

在温度随时间上升阶段，试验值比模拟值上升速率快，因所用碳纤维纱线较粗，上机织造时经纬密度较小，织物较稀疏，且碳纤维纱未加捻，在一定气流冲击下，织物受到压力作用使得纱线与纱线间易产生相对滑动，纱线间孔隙增大，导致织物的透气性较好[19]，热量易穿透织物到达织物背面，而在数值模拟计算过程中没有考虑压力的作用，导致试验值略高于模拟值，在今后的工作中需要进一步考虑热力耦合对气流冲击下织物传热性能的影响。

5 结 论

为研究织物在热流冲击下的热传递性能，基于织物中纱线的截面形状及其交织路径函数，建立碳纤维平纹织物的三维几何模型，基于传热学理论建立在热流冲击下织物中热传递的数值模型，预测热量在织物径向的传递过程，获得织物背面不同时刻温度的数值。自行搭建对流热冲击下织物传热过程测试的试验平台，利用红外热像仪对织物背面的温度进行非接触测试，将试验测试结果与数值模拟计算结果进行对比，当织物表面分别施加热流密度为1 319和1 103 W/m2载荷时，织物背面温度的模拟值和试验值的平均相对误差分别为6.64%和3.28%，说明所建立的数值模型能较好地反映碳纤维平纹织物的动态传热过程。建立碳纤维织物在热流冲击下传热过程的数值模型可为今后高温热流冲击下热防护纺织材料的设计、性能评估和优化提供预测依据。

FZXB