岬湾海岸海滩养护工程对水体交换的影响
匡翠萍, 董智超, 顾 杰, 李文斌
(1.同济大学 土木工程学院, 上海 200092; 2.上海海洋大学 海洋生态与环境学院, 上海 201306)
自然界砂质海岸岸线中有50%为岬湾型海岸,岬湾海岸因其独特的地貌特征,根据海滩稳定性特征,可以分为静态平衡海滩、动态平衡海滩和不稳定海滩[1].静态平衡海滩被当做一种稳定的岸线形式[2],在风暴侵蚀过后,被搬运的沙仍会恢复到沙滩上,形成一种天然自保机制[3].所以通过人工岬湾布置岬头使岸线与静态平衡海湾岸线重合,从而使海湾保持平衡和稳定[4].人类活动正在成为塑造地球表生系统最重要的营力,近岸海域受人类活动影响显著,农业施肥、工业排污等使入海营养盐和污染物大幅上升,导致近岸海域底质重金属、有机污染物严重超标,水体出现富营养化[5].岬湾海岸虽然有助于降低海滩和岸线受自然灾害侵蚀的风险,但由于其两侧岬头对沿岸流的阻碍作用,使岬湾内动力条件减弱,降低了近岸水体的自净能力,河口排污稀释扩散能力下降[6],近岸海域水质恶化[7],藻华[8]等现象频发.PAN等[9]认为在靠近岬头端部设计一定宽度的潮汐通道,以减弱可以接受程度的岸线保护效果为代价,可以有效加快岬湾海岸的水体交换能力,改善岬湾内水质状况.
在长期针对近岸海域水环境问题的探索过程中,人们发现海洋环境中污染物在水体中受到物理、化学和生物过程的共同影响[10],水体环境的改善最终归结为对污染物归宿的控制[11].随着海域的涨落潮过程,海岸环境中污染物浓度可以与外界的水体发生交换并得到稀释[12],通过量化水体输运过程和其规律,研究水体交换能力的强弱,可以有效反映水体的自净能力.采用数学模型研究海域水体交换能力是较为快速和有效的手段,主要分为拉格朗日法[13]和欧拉法[14].拉格朗日法基于粒子追踪,可有效避免数值耗散产生的不稳定,但忽略了水体的对流扩散作用[15].欧拉法基于对流扩散方程求解,反映局地余流特征,对于运移轨迹和归宿问题存在局限性[16].
海滩养护工程是当前抵御海岸侵蚀灾害环境友好的对策,通过向海滩大量抛沙,使海岸平均高潮位以上海滩后滨的宽度迅速得以增加,辅以导堤促淤、外防波堤(或潜堤)掩护等措施,达到增宽和稳定海滩的目的.张宇等[17]采用DELFT3D建立工程区海域潮流数学模型,模拟发现在海区岬角处修建突堤和修筑离岸潜堤工程将显著减小工程区内潮流流速,利于养滩的形成和稳定.刘会欣等[18]采用数值模拟结合物理模型试验方式,研究了北戴河新区岸线在养滩工程后的稳定性,认为人工养滩工程同时辅以人工沙坝,能够较好保持北戴河新区岸线的稳定.杨燕雄等[19]则应用了数值模拟和物理试验探讨研究了沙坝的养滩作用,并通过北戴河养滩工程证实了人工近岸沙坝在海滩养护工程中遮蔽功效.
针对岬湾海岸的海滩养护工程,诸多学者研究的视角多集中在海滩养护工程对水动力和工程稳定性的影响,而海滩养护工程对水环境的影响研究较少,本文以秦皇岛新开河口至南山人工岬湾海岸为例,基于水动力和保守物质输运模型,采用欧拉法计算滞留时间来定量分析水体交换能力,研究滩肩补沙和水下沙坝工程对近岸海域水动力和水体交换的影响,以期对工程的设计规划及岬湾海岸水环境的改善提供一定的参考依据.
1 研究区域及工程布置
河北省秦皇岛位于渤海湾与辽东湾交汇处,是河北省著名的沿海城市.海域潮流基本属于正规半日潮流,表现为顺岸往复流,涨潮流主要为西南偏西(WSW)向,落潮流为东北偏东(ENE)向,潮流方向与岸线、等深线基本平行.秦皇岛海域波浪主要为风浪和以风浪为主的混合浪,约占全年频率的75%;涌浪及以涌浪为主的混合浪约占全年频率22%.海域波高值总体较小,一般小于0.5 m.
秦皇岛海港区新开河口至南山岸线海滩侵蚀不断加剧:滩面束窄、岸坡变陡、组成物质粗化,部分岸线沙滩滩肩已基本消失,区内东山浴场海滩生态功能和旅游休憩价值显著下降同时威胁近岸建筑.本次海滩修复工程为滩肩补沙与两座水下沙坝吹填.补沙岸线长1.1 km,将人工沙滩的上限高程(即滩肩高程)设置为2.0 m(85国家高程基准),滩肩由陆向海为小于1∶100的缓坡形式,设计高水位以下剖面坡度为1∶10,直至与自然海床相交,整体向海拓宽沙滩30~50 m.吹填的两座水下人工沙坝离岸约200 m,每段沙坝长200 m,底宽80 m,坝顶宽60 m,坝顶高程-0.9 m.海滩养护工程布置如图1所示.图中,Y0,Y1和Y2为模型验证点位.NE,SE和SW为模型外海开边界.
2 数学模型的建立和验证
MIKE 21模型是丹麦水力学研究所(DHI)研发的通用数学模拟系统软件,主要模拟河流、湖泊、河口、海洋及海岸的水流、波浪、泥沙及水环境.采用MIKE 21中水动力模块、波浪模块和物质输运模块分别建立秦皇岛海域潮流、波浪和保守物质输运模型.模型通过有限体积法进行离散,显式欧拉法进行求解,同时具备计算速度快和计算精度高的特点[20].
2.1 基本控制方程
2.1.1潮流模型
潮流模型建立在Navier-Stokes方程的基础上.在笛卡尔坐标系下,通过对三维水平动量方程和连续方程沿水深积分得到二维浅水方程:
(1)
(2)
(3)
式(1)~(3)中:t为时间;x、y为笛卡尔坐标下纵、横坐标;h为总水深,h=η+d,η为水位,d为静止水深;u、v分别为x、y方向的水深平均流速;Sf为源汇项,f为科氏力系数;ρ0为水的密度;sxx、syy、sxy和syx为辐射应力分量;pa为大气压力;τsx,τsy分别为x、y方向上的表面风应力;τbx,τby分别为x、y方向的底床切应力;侧应力Tij包括黏性力和紊动力等,通过水深平均流速梯度由涡黏方程计算,公式如下:
(4)
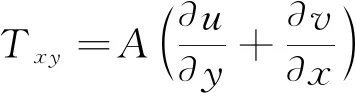
(5)
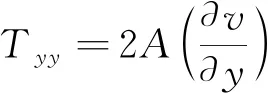
(6)
亚网格尺度涡流黏度A由Samagorinsky公式(7)确定:
(7)
式中:cs为常数,取0.28;l为特征长度;变形率Sij根据下式计算:
(8)
2.1.2波浪模型
MIKE 21波浪模块采用的是非结构网格下的风成波浪谱模型,可以对近岸海域风成浪和涌浪的成长、消散与传播变形进行模拟.在笛卡尔坐标系下,模型的控制方程为:
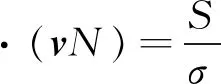
(9)
式中:N(x,σ,θ,t)为波作用密度;σ为相对角频率;θ为波向;v=(cx,cy,cσ,cθ)为波群的推进速度;cx、cy为波浪在x、y方向上的传播速度分量;cσ、cθ为波浪在σ,θ方向上的传播(变形)速度分量;S是以谱密度表示的源函数;▽为四维梯度算子.
(10)
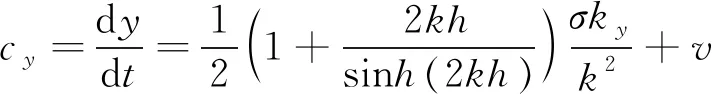
(11)
(12)
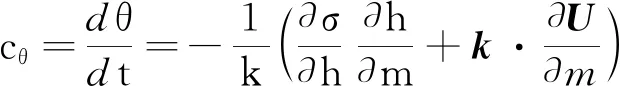
(13)
式(10)~(13)中:kx、ky为波数矢量k在x和y方向上的分量;s为沿波浪方向θ上的空间坐标;m为垂直于s的坐标;▽x为x空间的二维微分算子;cg为波群速度大小.
2.1.3保守物质输运模型
保守物质输运方程为
(14)
式中:C为保守物质浓度;εx和εy为对流扩散系数.
2.2 模型计算范围和网格
为保证计算精度同时考虑计算效率,建立渤海和秦皇岛海域的双重嵌套模型,为保证计算边界不受到新开河口至南山岸线海滩养护工程的影响,秦皇岛海域模型陆地岸线南起团林乡,北至甘家村(图1),模型向外海延伸大约46 km.模型采用非结构网格对研究区域进行剖分,网格节点数为4 888个,网格单元数为9 099个,网格从外海到岸线由疏到密,外海边界分辨率约为4 km,新开河口至南山岸线最大分辨率为5 m.
2.3 模型参数选取及边界条件
模型开边界包括NE(东北)、SE(东南)、SW(西南)三个开边界,NE和SW外海开边界的走向基本与主流方向垂直,从而增强模型的稳定性.采用流速和潮位控制的Flather边界条件,由渤海大模型[21]提供.固边界采用不可滑移条件,即流速为0.涡粘性系数采用Samagorinsky亚网格尺度模型来计算水平涡粘系数,其中常数CS取为0.28,涡粘系数A上下限分别取为1.0×1010和1.8×10-6m2·s-1.曼宁数根据底部泥沙粒径分布,区域均值为74 m1/3·s-1,时间步长取60 s.海岸边界采用动边界模拟滩肩和潮间带的干湿交换过程,取干点临界值hdry=0.005 m,淹没临界值hflood=0.05 m,湿点临界值hwet=0.1 m.物质输运模型中初始条件设置计算区域为单位浓度示踪物质,其他区域为0,且外海边界条件均设置为0以模拟外海水体与研究水体的交换过程.
2.4 模型验证
秦皇岛潮流模型潮位选取了秦皇岛测站(Y0)验证,时间为2013年5月16日0:00至5月17日24:00,同时对秦皇岛海域的9个测站进行流速、流向多次验证,时间为2013年5月16日08:00至5月17日08:00,其中具有代表性的Y1、Y2二个测站验证结果如图2所示,可以看出Y0点计算的潮位过程与实测潮位过程较为一致,Y1与Y2点模拟流速、流向过程与实测数据在数值和相位上吻合较好.
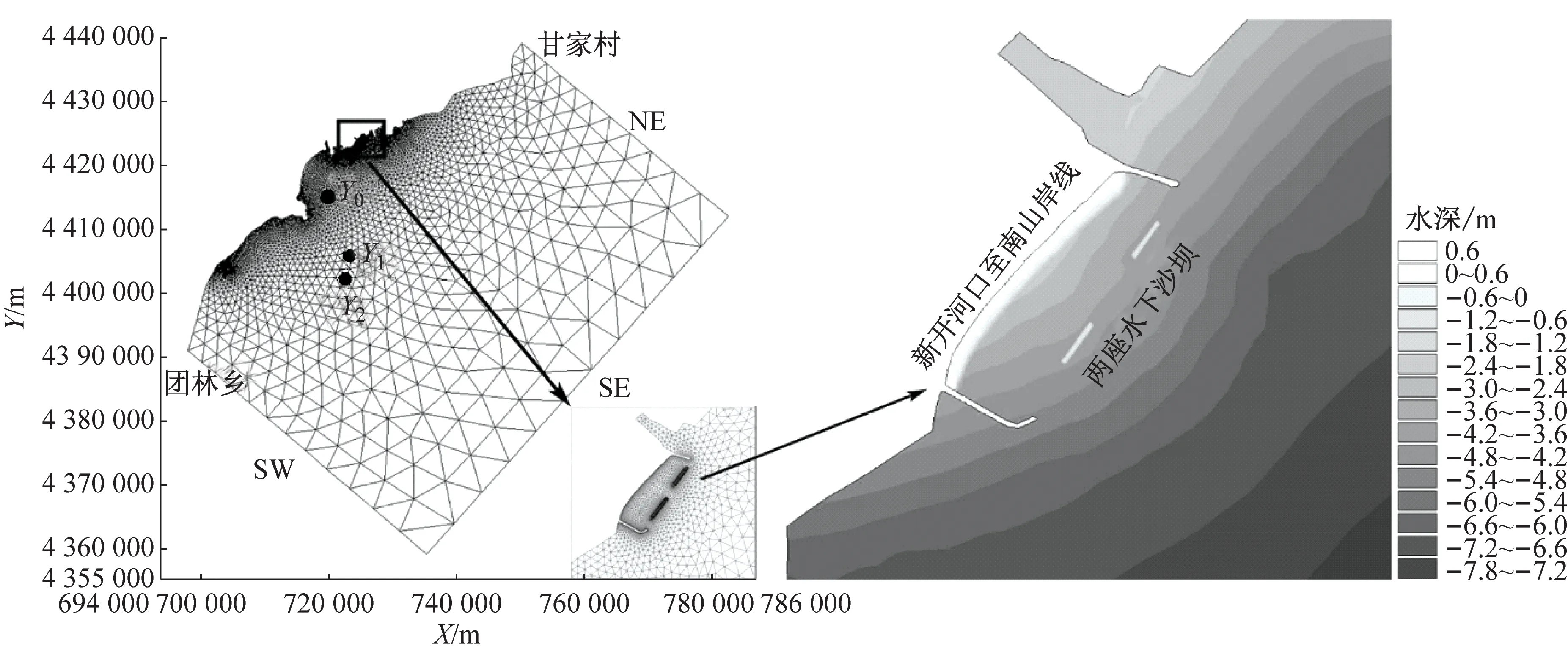
图1 模型网格及海滩养护工程
Fig.1 Mesh of Model and Beach Nourishment Project
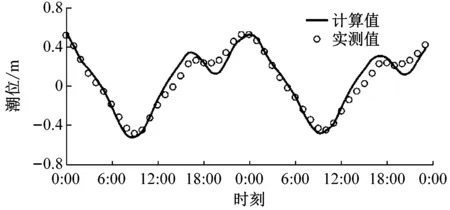
a Y0,潮位
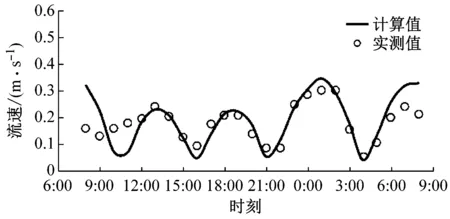
b Y1,流速 c Y1,流向
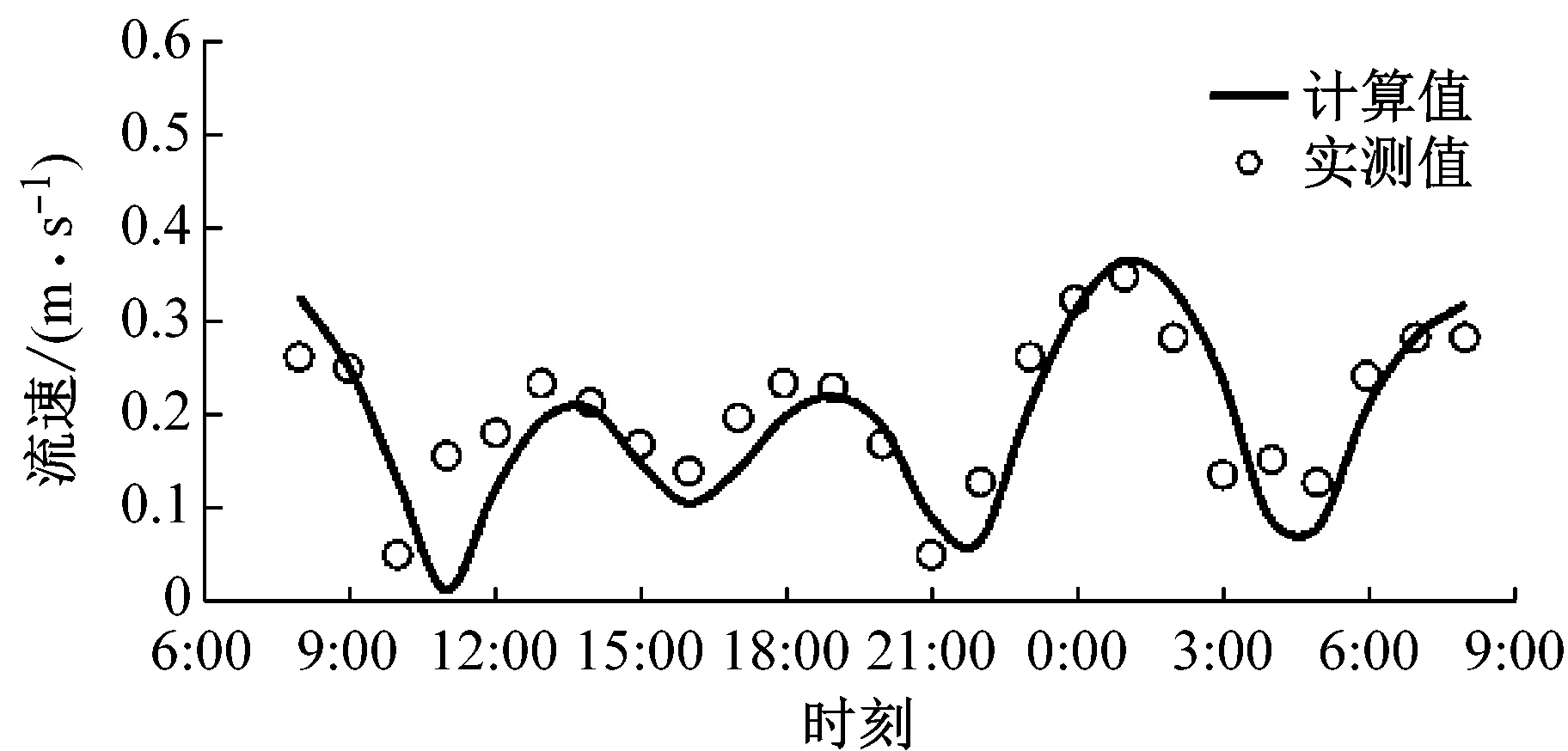
d Y2,流速 e Y2,流向
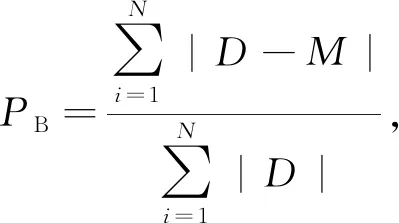
3 数学模型的建立和验证
3.1 滞留时间定义及研究分区
滞留时间定义为初始的单位浓度的示踪物质衰减(此处衰减为动力作用引起的浓度降低,非化学衰减)到某一(如e-1、50%或10%)初始质量所需要的时间,通过实验或数值模拟得到浓度变化过程,计算出相对质量变化过程,用最小二乘法进行曲线拟合,确定衰减系数后进而计算得到滞留时间.随时间变化的剩余示踪剂质量与初始示踪剂质量之比的衰减函数可表示为
Mt/M0=βe-kt+Q
(15)
式中:Mt和M0分别为示踪剂在时刻t和初始时刻t0的质量;参数β、k和Q利用最小二乘法拟合求得.
为研究海滩养护工程前后水体交换特性变化,将岬湾内部分为如图3所示的三个子区域:图3a为岬湾内部区域,图3b为将岬湾内部区域划分为三个子区域,其中A为西侧沙坝掩护子区域,B区域为东侧沙坝掩护子区域,C为两沙坝之间子区域.
3.2 工程前后流场分析
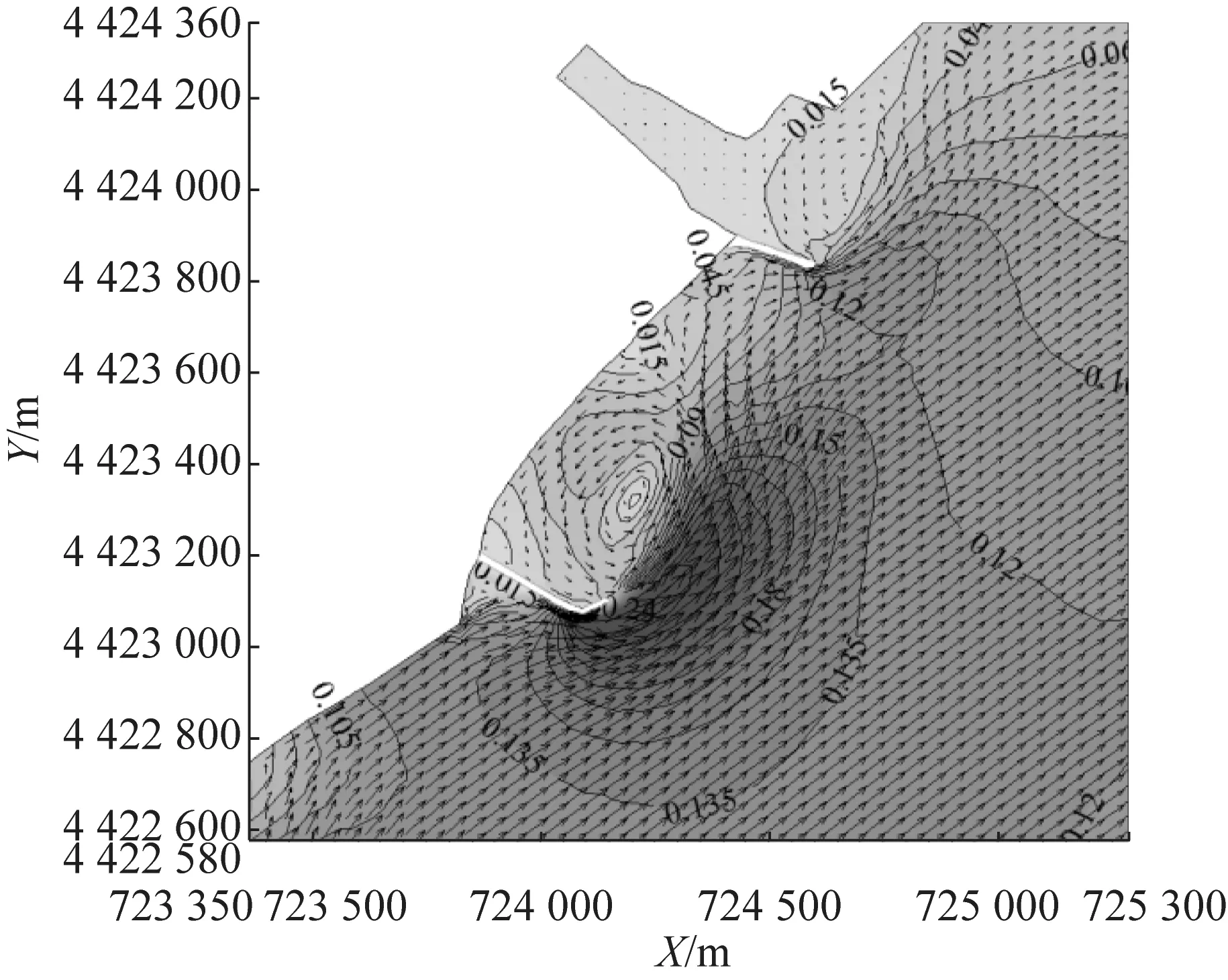
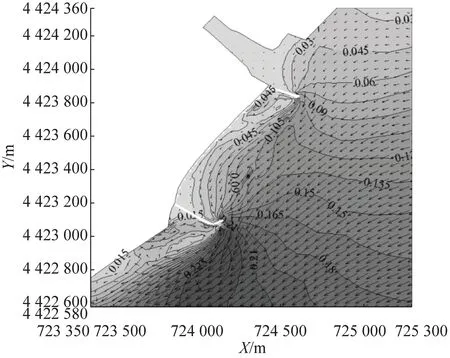
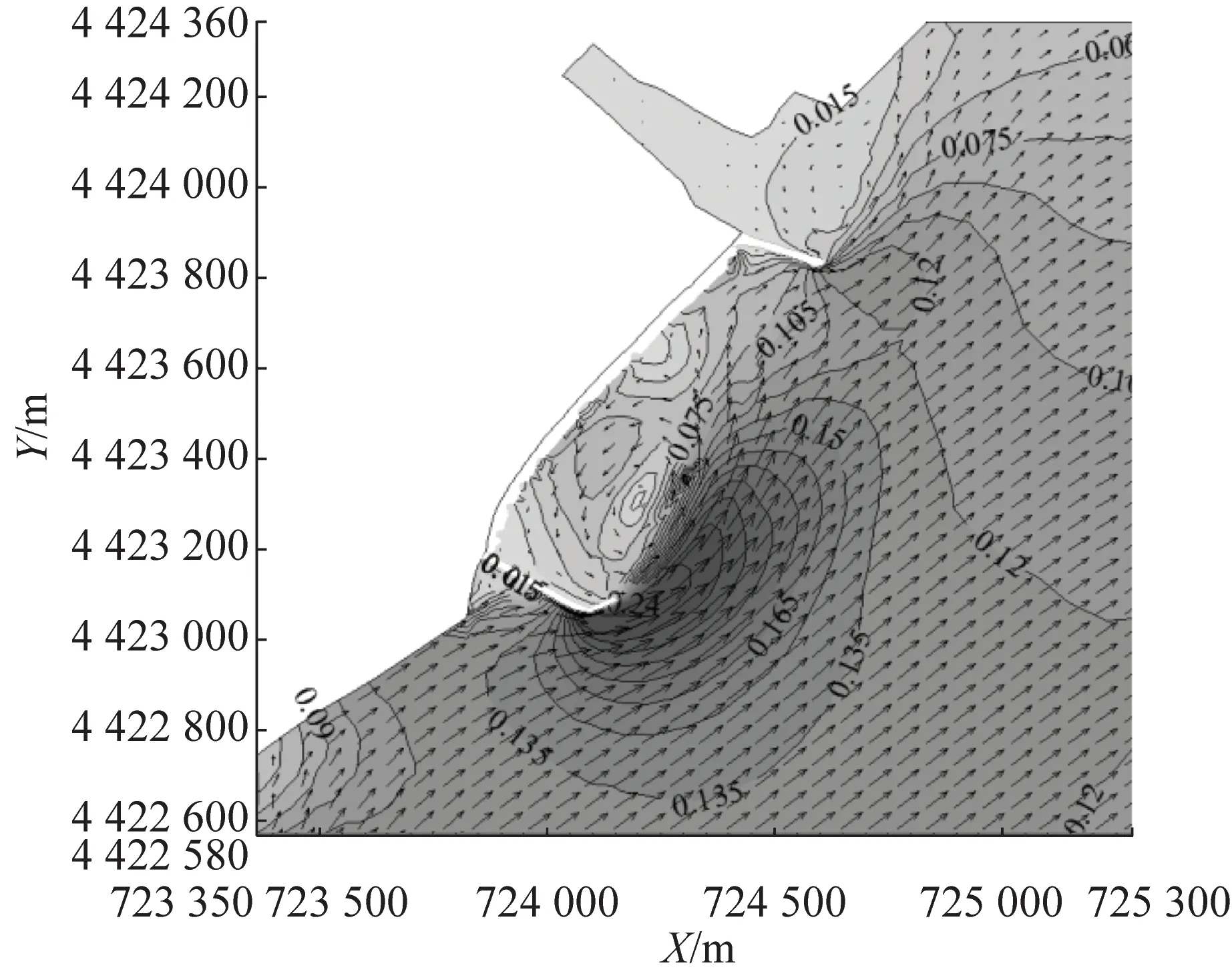
图4和图5分别为新开河口至南山近岸海域涨落急时刻海滩养护工程前和工程后的流场,图中的等值线为流速值.由于水下沙坝与水流走向保持基本平行,沙坝顶托水流且起到一定的导流作用,流速变化主要发生在滩肩、沙坝坝顶、沙坝后侧以及两个沙坝之间的水流通道.
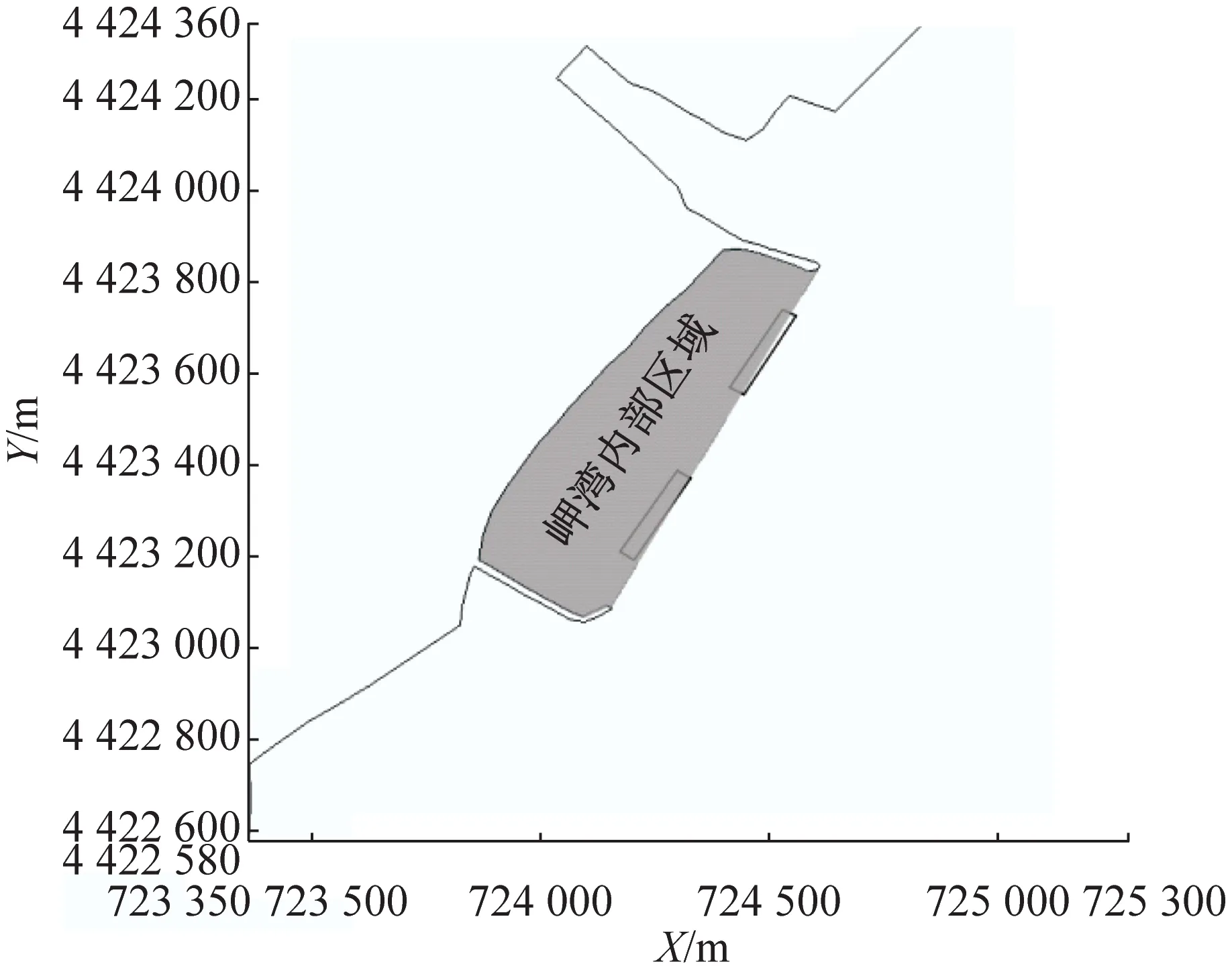
a 岬湾内部区域
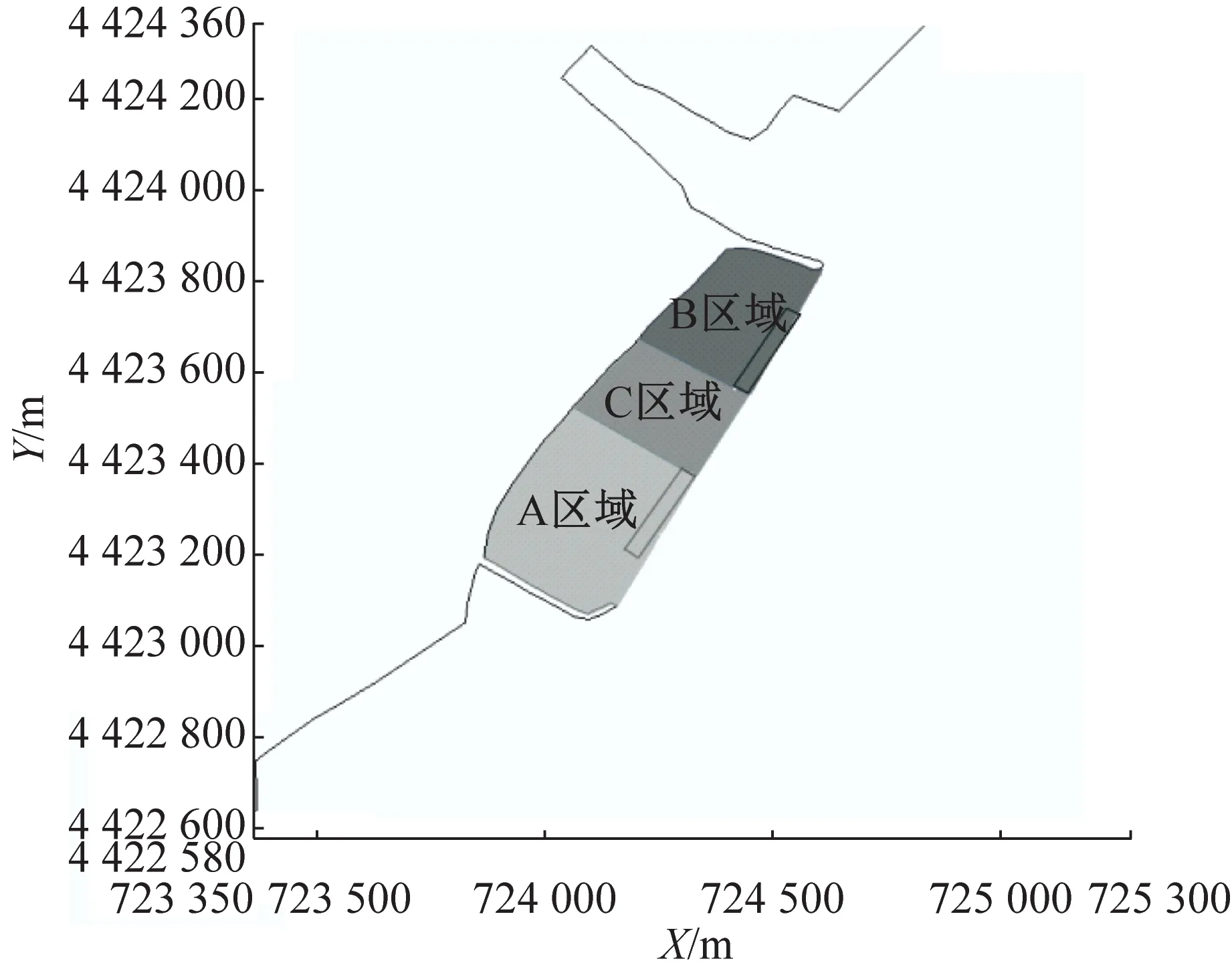
b 岬湾内部三个子区域
涨急时刻:沙坝坝顶处,由于顶托作用流速增加约0.02~0.03 m·s-1;两沙坝间流速减小约0.015 m·s-1,沙坝与岬头间形成潮汐通道流速增加约0.01 m·s-1,滩肩补沙使得岸滩前段向海前移,两沙坝后侧的滩肩处流速减小0.04~0.07 m·s-1,其余滩肩处流速减小较少约0.01~0.02 m·s-1.落急时刻:与涨急时刻流速变化区域分布相似,沙坝坝顶处流速增加约0.02 m·s-1;两沙坝间流速减小约0.01 m·s-1,沙坝与岬头间流速增加约0.01 m·s-1,两座沙坝后侧滩肩位置流速减少约0.05~0.06 m·s-1,其余滩肩处流速减小约0.01~0.02 m·s-1.
3.3 不同动力情景设置
由水体驱动动力来看,影响滞留时间的主要因素为潮流、波浪和风,波浪受风影响,为研究波浪和风对水体交换影响情况,设置纯潮流、潮流与波浪耦合、潮流与风场耦合、潮流、波浪与风场耦合4种不同动力条件的情景进行对比分析,设置4种情景如表1所示,风场条件参考所统计风况,风速5.0 m·s-1,风向为北偏东40°.波浪场条件参考所统计出的具有代表性的常浪浪况:周期为4.06 s,波高为0.30 m,波向为155.2°.“√”和“×”号分别表示对应情景下该影响因素加入、不加入.

a 涨急
b 落急
a 涨急
b 落急
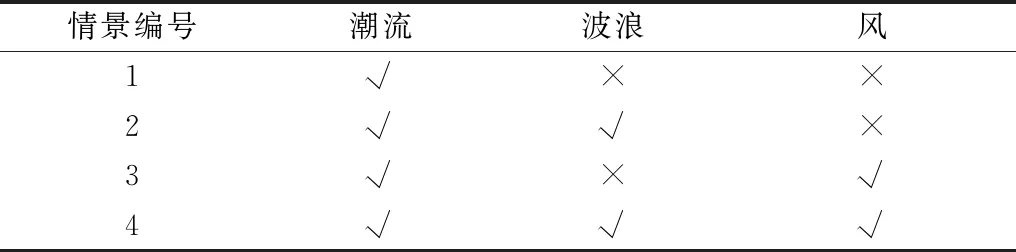
表1 不同动力情景
3.4 滞留时间对工程的响应特征分析
不同情景工程前、后滞留时间如图6所示.不同区域4种情景下,由于沙坝与人工岬头形成的潮汐通道使得靠近岬头处流速增加,流速增加约0.01~0.03 m·s-1,水动力条件增强,水体交换加快.A区域和B区域由于沙坝顶托作用的影响,流速增加0.02~0.03 m·s-1,在不同情景条件下滞留时间减少约6.6 %~23.9 %,而C区域由于未设置沙坝,与外海直接连通,和工程前条件接近,即使受到A、B区域的共同影响,滞留时间有所降低,但变化幅度很小.整体而言,由于工程进行了滩肩补沙,水深变浅,岬湾内部区域水体减少,水体更易于发生整体交换,滞留时间缩短,而且两座水下沙坝的吹填,虽然较工程前对水体有遮蔽作用,但是岬头与沙坝之间预留的潮汐通道及沙坝顶托的流速增加,加快了岬湾内部区域的水体交换,岬湾内部区域工程后较工程前的滞留时间缩短,减少约5.6 %~16.0 %.
a 情景1
b 情景2
c 情景3
d 情景4
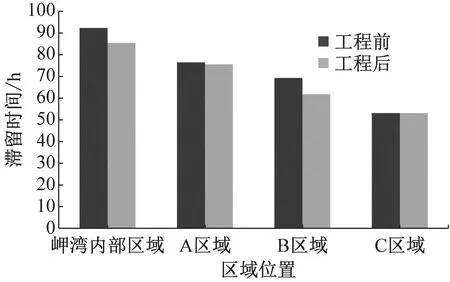
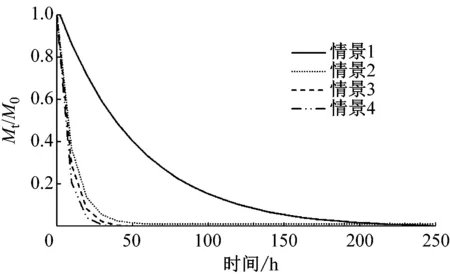
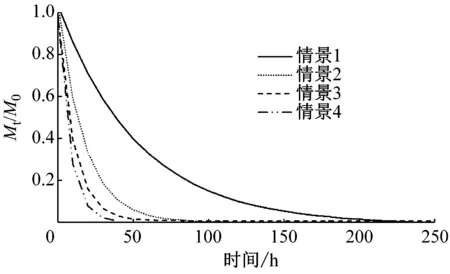
3.5 滞留时间对动力因素响应分析
工程前岬湾内部区域、A、B、C子区域4种情景的滞留时间如图7所示.整体上,波浪、风场及波浪和风场同时作用均会促进水体交换,情景1滞留时间最长,情景2、情景3滞留时间相对于情景1减少70.5%、78.7%,情景4,即潮流、波浪与风场同时驱动下,岬湾内部区域、A、B、C区域滞留时间最短,相对情景1滞留时间减少83.2%.
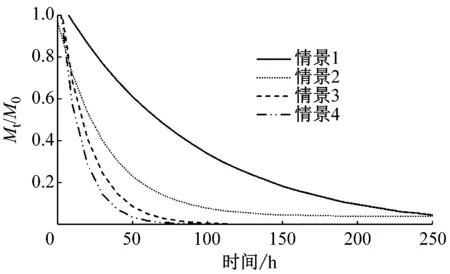
a 岬湾内部区域

b A区域
c B区域
d C区域
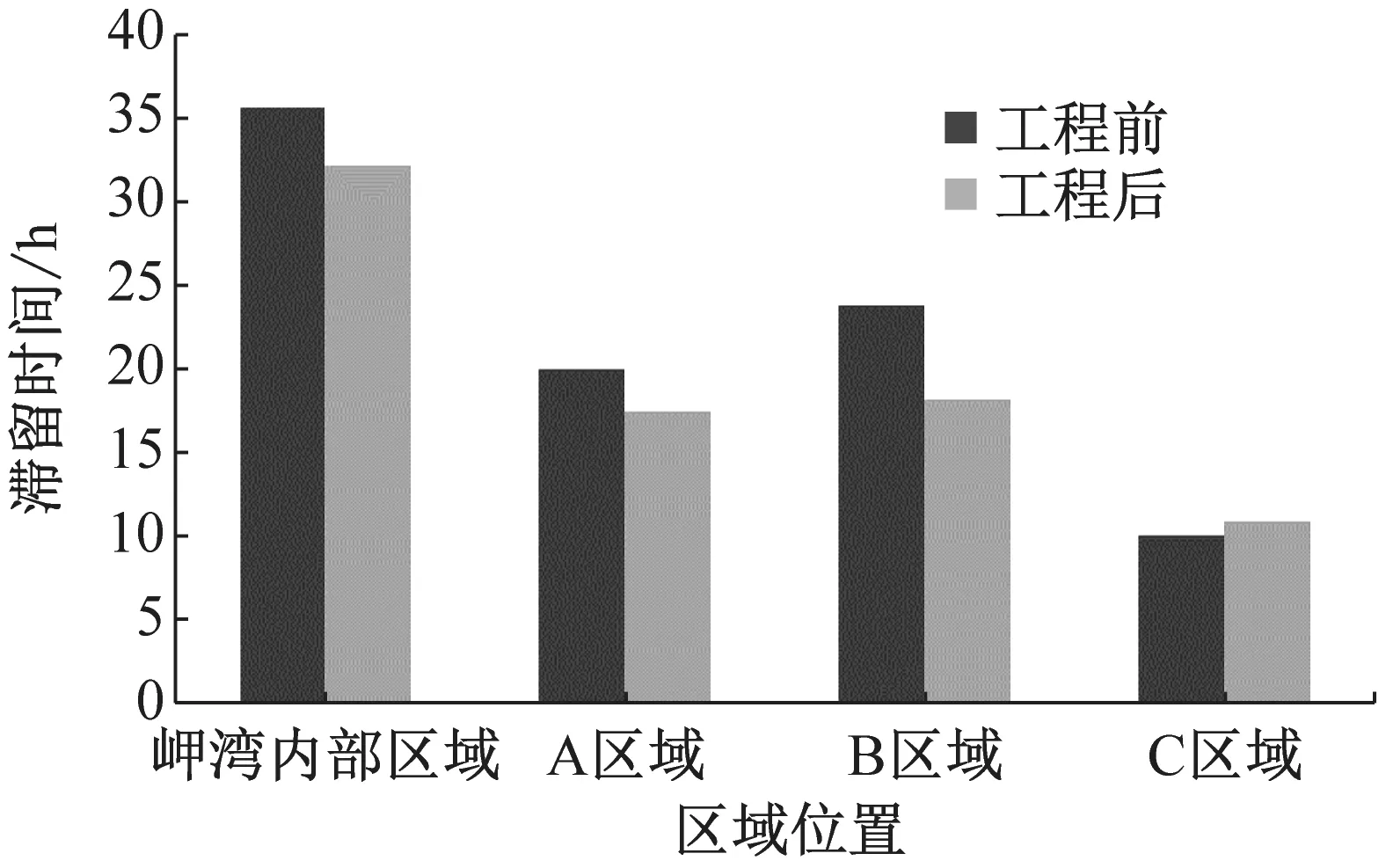
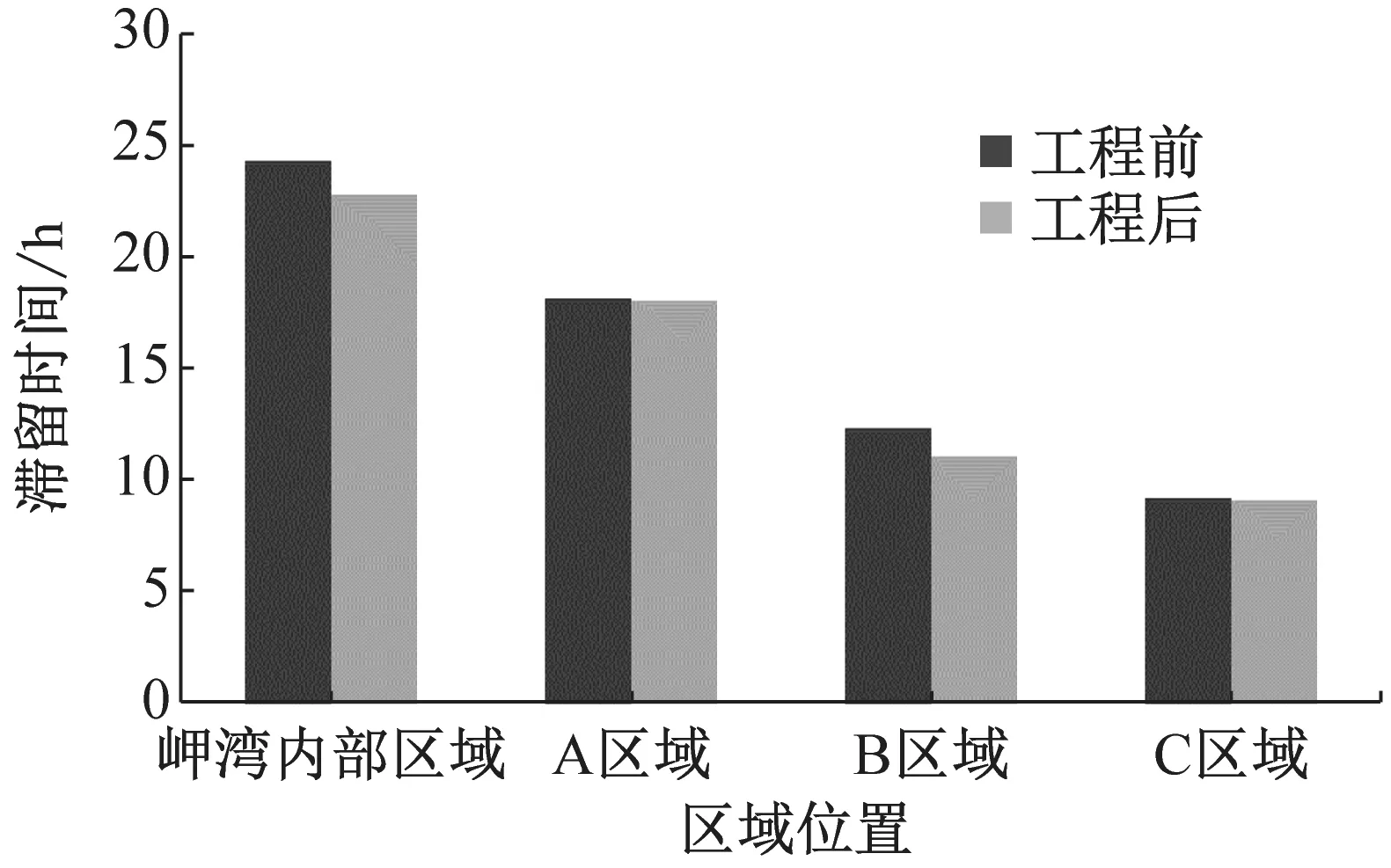
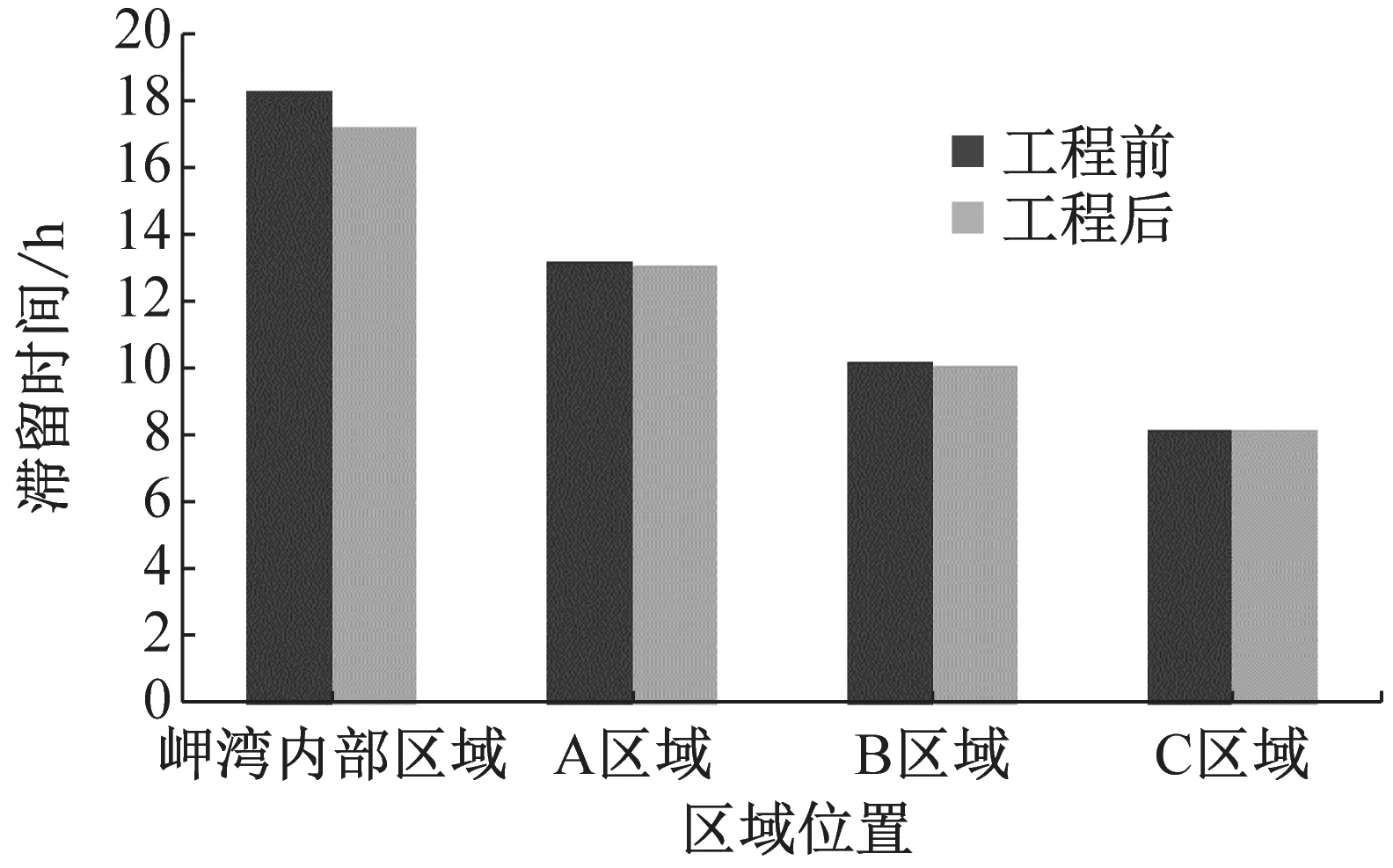
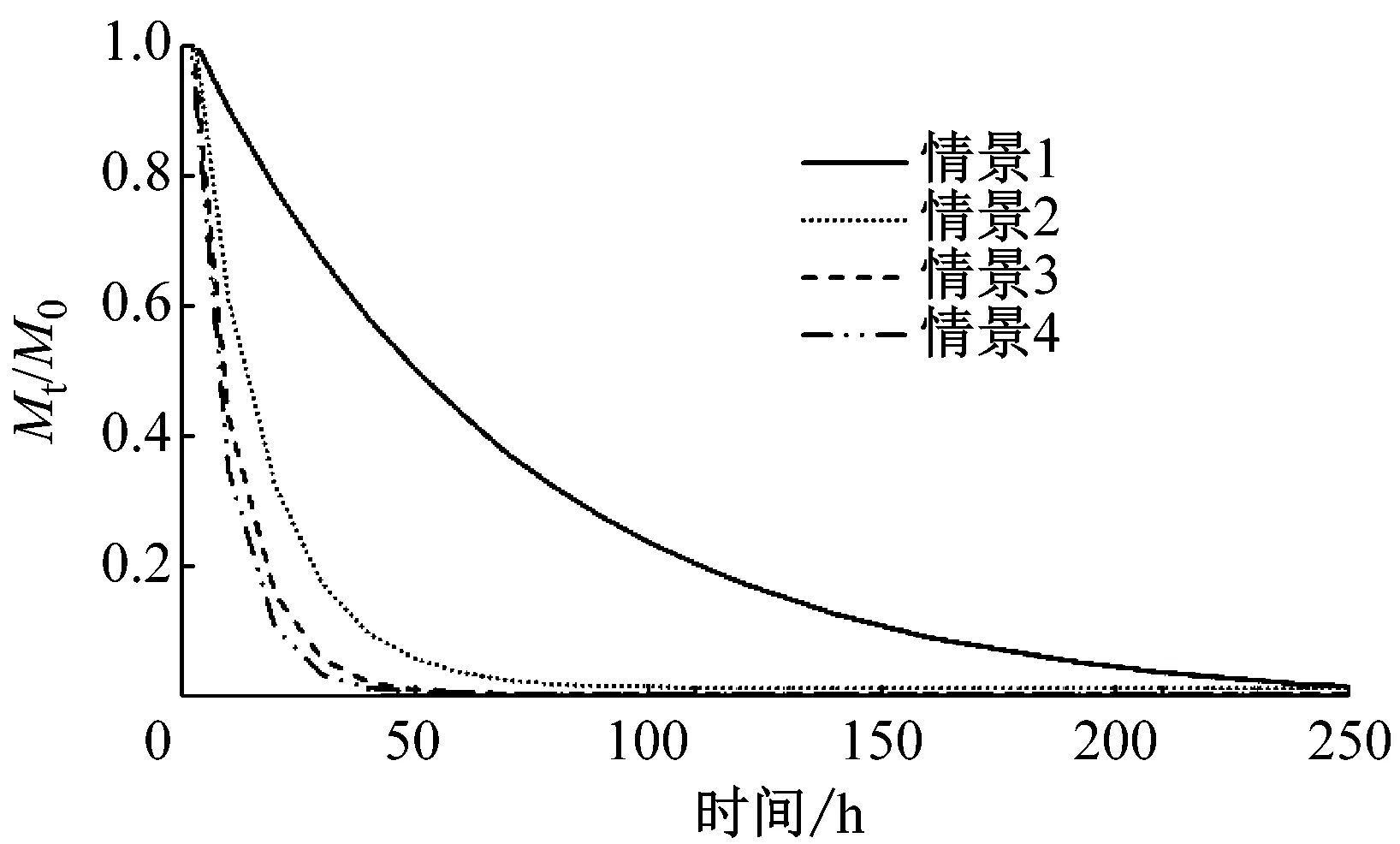
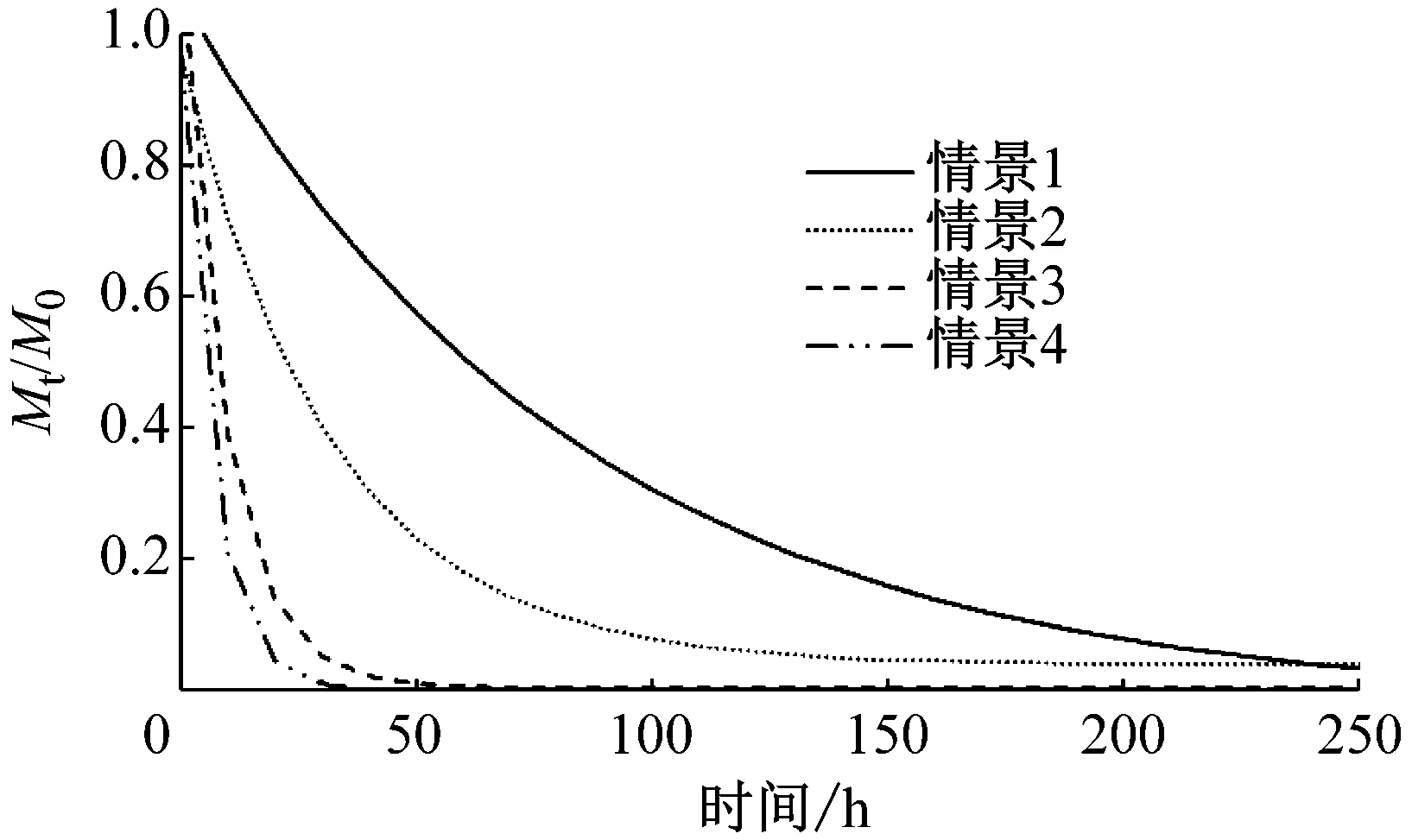
工程后岬湾内部区域、A、B、C子区域4种情景的滞留时间如图8所示.工程后不同情景条件下滞留时间及对滞留时间的削减率如表2所示,由于波浪受到风场影响,波浪和风场共同作用下的滞留时间较波浪和风单独作用条件下的滞留时间更短,以岬湾内部区域为例,情景2对滞留时间的削减效果为62%,情景3对滞留时间的削减效果为73%,情景4对滞留时间的削减效果为80%,削减效果越大即对水体交换的改善效果越好,情景4是情景2和情景3的叠加,而对滞留时间的影响不是线性叠加关系,且不同区域水体的影响效果也不同,由于C区域位于两个离岸沙坝的开口处,与外海水体不存在遮挡,而A、B区域部分受到离岸沙坝的遮蔽作用,风和波浪及其单独作用对C区域的影响均大于A和B区域,这主要是由于不同区域水工结构和地形的不一致导致水动力条件存在差异.
a 岬湾内部区域
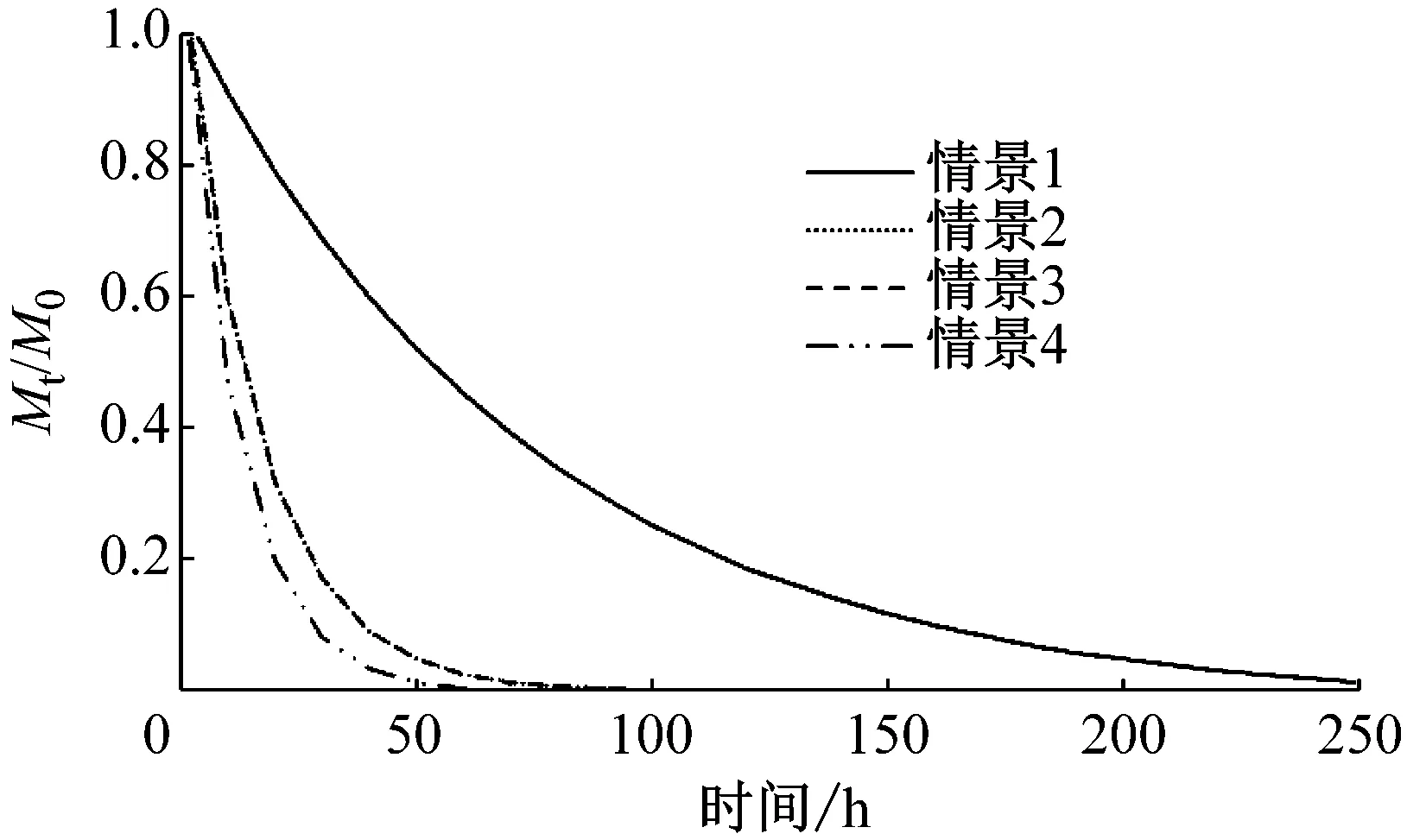
b A区域

c B区域
d C区域

情景岬湾内部区域A区域B区域C区域滞留时间/h削减率/%滞留时间/h削减率/%滞留时间/h削减率/%滞留时间/h削减率/%1潮流85.375.361.553.12潮流+波浪32.26217.47718.17110.8803潮流+风22.87318.17611.1829.1834潮流+风+波浪17.28013.18310.1848.285
4 结论
基于MIKE 21软件建立了研究区域二维潮流和物质输运模型,利用率定和验证好的模型进行工程前后和不同动力情景的数值模拟,采用时间尺度指标定量衡量水体交换对海滩养护的响应,得到水体交换对岬湾内海滩养护的响应特征:
(1) 工程后,涨落急时刻,沙坝坝顶处由于顶托作用流速增加0.02~0.03 m·s-1;两沙坝间通道减小0.01~0.015 m·s-1.岬头与沙坝形成潮汐通道使得靠近岬头处流速增加约0.01 m·s-1;滩肩补沙使得岸滩前段向海前移,滩肩前方海域整体流速减小,两沙坝后侧的流速减少更多.
(2) 沙坝与岬头间形成潮汐通道由于流速增加0.01~0.02 m·s-1,使得工程后内外水体交换速度加快,滞留时间相较于工程前缩短,水体交换能力增强.
(3) 工程后,岬湾内部区域和三个子三区滞留时间变化不同,岬湾内部区域滞留时间减少量较多,减少约5.6%~16.0%,A区域与B区域为西、东两侧岬头掩护区域,滞留时间减少约6.6%~23.9%,C区域滞留时间变化不明显.
(4) 波浪和风场加入后使得滞留时间减少约83%,波浪加入后滞留时间减少约78%,风场加入后滞留时间减小约71%~72%.但由于波浪受到风场影响,波浪和风场共同作用下滞留时间不为单独条件下的线性叠加关系.

