板料成形快速模拟的中间构形构造方法
刘永财, 鲍益东, 秦雪娇, 刘玉琳, 陈文亮
(1. 南京航空航天大学 江苏省精密与微细制造技术重点实验室, 南京 210016;2. 曲靖师范学院 数学与统计学院, 云南 曲靖 655011; 3. 美国工程技术联合公司, 南京 210016)
在金属板料成形的模拟方法中[1],为了弥补一步逆成形法模拟的应力精度不高的问题[2-3],提出了引入中间构形的多步成形有限元模拟方法并得到了广泛应用[4-5].其中,构造中间构形是多步成形法中的一个关键技术.相关研究包括:Lee等[6]采用线弹性反向映射法计算中间构形,并将中间构形视为从初始板料构形到最终板料构形的线弹性变形过程的中间过程;Guo等[7]考虑轴对称问题,利用最小面积法构造中间构形,将三维中间构形转化为二维中间构形;刘伟杰等[8-9]采用伪最小面积法构造滑移约束面,以降低对零件形状的依赖性;Shirin等[10]将最终零件的网格向初始坯料所在的平面投影并利用网格展开进行求解;陈伟等[11]采用比例插值方法在初始构形与最终构形之间进行插值以构造中间构形.
本文提出了一种基于预应力膜单元的板料中间构形的平衡迭代计算方法,以适应复杂的零件形状,并将其集成到自主研发的基于大步长静力隐式有限元模拟分析软件QuickForm中,通过典型汽车零件的应用验证其有效性和准确性.
1 弯曲与解耦计算的基本原理
对于金属薄板成形来说,由于剪切变形对整个板料成形结果的影响较小,所以板料变形被看作由弯曲变形和拉伸变形构成.解耦是将板料的弯曲变形和拉伸变形过程分开进行求解,如图1所示.采用解耦技术可将板料成形的模拟过程分为弯曲变形和拉伸变形来求解.前者是求解板料在当前模具作用下的构形,因此,可以采用一种相对简单的方法求解以提高计算效率;后者是在弯曲变形所求板料中间构形的基础上,将板料的拉伸变形限定在中间构形上,并对包含弯曲效应的膜刚度所引起的拉伸变形进行求解.由于在拉伸变形的平衡迭代过程中,板料节点的运动被限定在由中间构形确定的滑移约束面上,只需考虑滑移约束面上两个方向的位移,所以降低了节点的自由度线性方程组的刚度系数矩阵的条件数,从而有效地提高了求解效率.
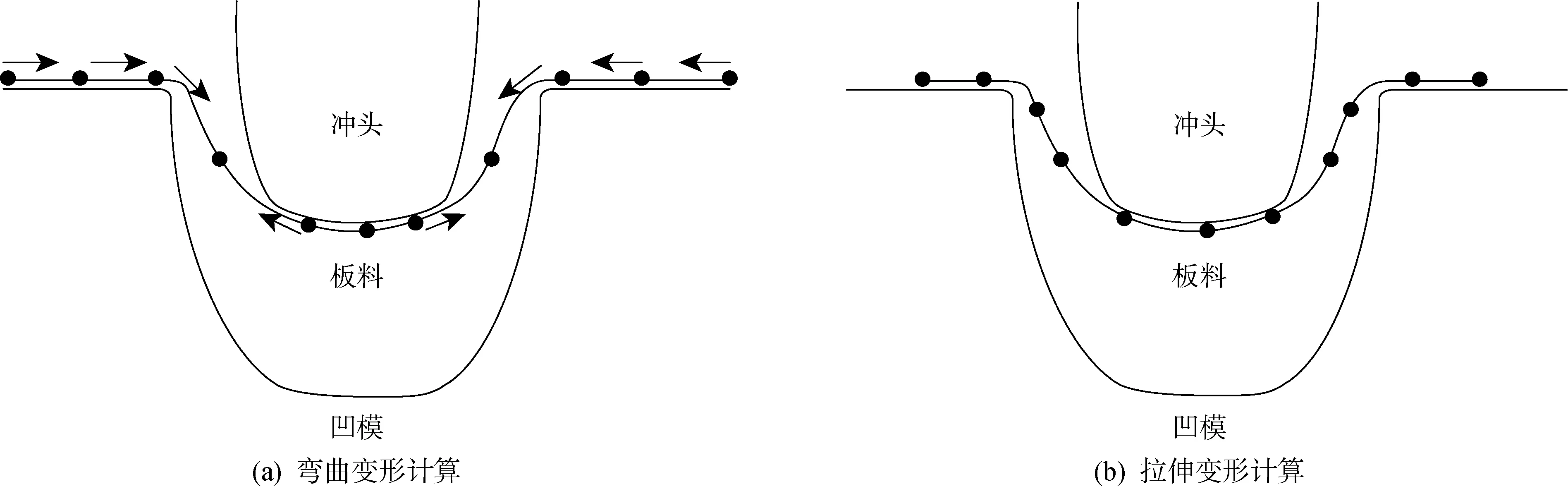
图1 解耦计算的原理示意图Fig.1 Diagram of principle of decoupling calculation
2 基于预应力膜单元的中间构形算法
2.1 算法的基本流程
假设已计算出上一个时间步的板料构形,则在该构形的基础上计算当前时间步的中间构形.本文以双动冲压成形为例进行说明.具体计算步骤如下:
(1) 判断板料与压边圈以及凹模的接触情况.寻找板料与压边圈相互接触的节点,接触节点应附着在凹模上,并对其进行固定约束,且在计算过程中节点的位置不变.
(2) 判断板料与凸模的接触情况.在双动冲压过程中,凹模始终固定,凸模每行进一个步长,与板料就有可能发生穿透现象.本文采用节点接触判断算法将穿透凸模表面的节点通过投影操作拉至凸模表面.
(3) 确定非接触区.根据位移计算拉至凸模表面的板料节点的内力,以确定节点力的状态.如果节点受到向外的拉力,则将其添加到非接触区节点集合中;否则,将其约束在凸模表面,并添加到约束节点集合中.
(4) 计算中间构形.采用迭代方法求解预应力膜单元的平衡状态方程,计算出非接触区域板料中间构形的形状,而接触区域板料中间构形的形状由凸模或凹模形状来确定.
重复步骤(1)~(4),直到中间构形的所有单元都满足预应力膜单元的平衡条件,从而完成当前增量步的中间构形构造,算法的流程如图2所示.类似地,可将上述算法推广到单动冲压成形的模拟.
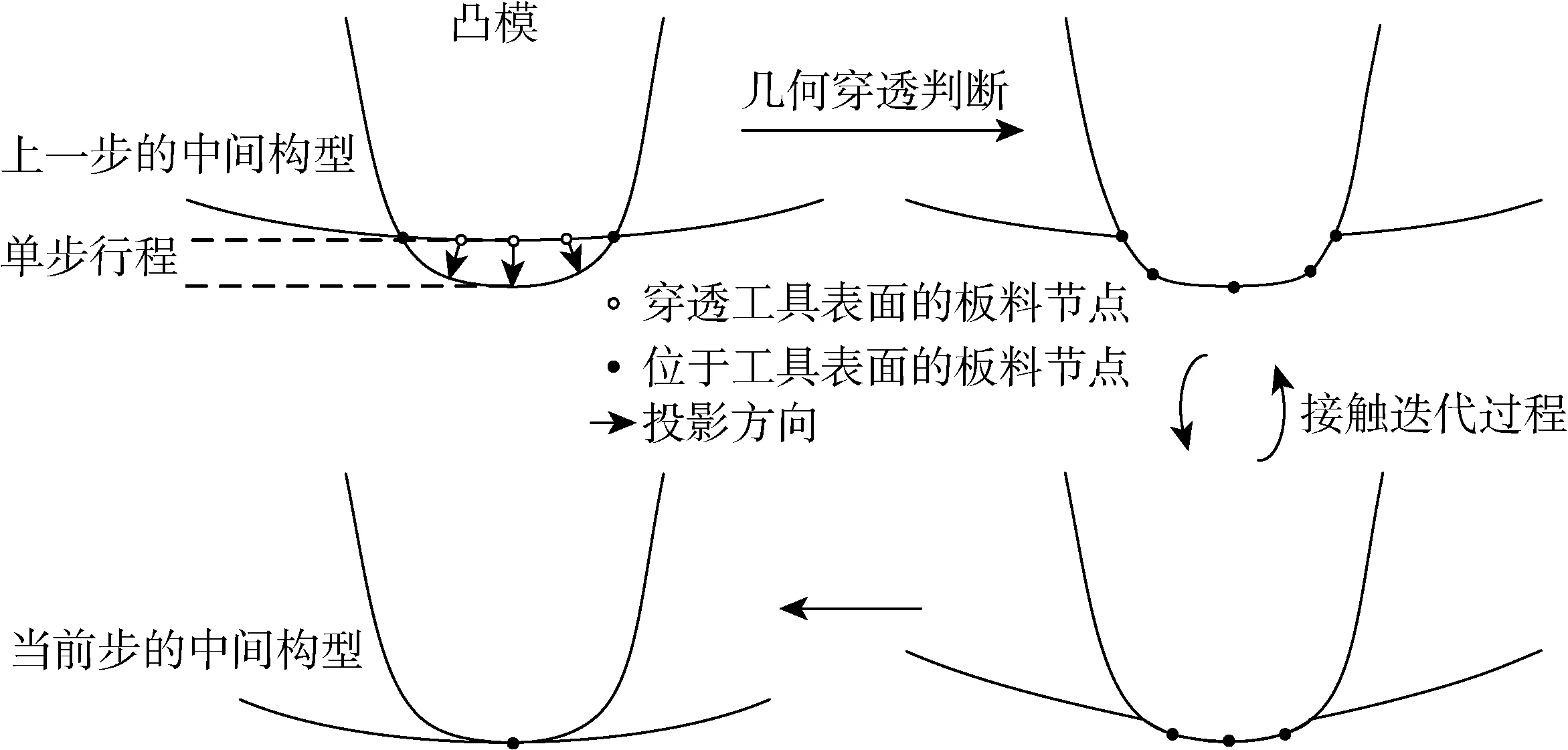
图2 中间构形的计算流程Fig.2 Calculation flow of intermediate configuration
2.2 节点与模具接触判断算法
判断板料节点与模具接触时,首先采用搜索算法确定节点沿法线方向投影到模具表面的投影单元,进而确定投影点.在确定投影单元时,运用划分空间格的方法搜索与板料节点距离最近的模具节点,根据模具表面节点与单元的拓扑关系来确定投影单元的范围,从而缩小搜索范围,提高搜索速度.
确定投影点后,根据几何关系判断节点是否穿透模具表面,如图3所示.具体计算公式为
g(xs)=(xs-xm)·n(xm)
(1)
式中:g为节点穿透量;xs为板料节点位置;xm为板料节点xs沿节点法线方向投影至模具表面的节点位置;n(xm)表示节点xm所在投影单元的外法线方向.
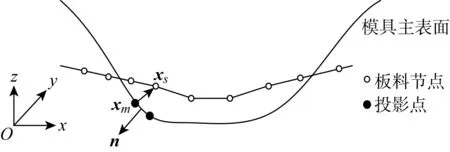
图3 节点穿透判断示意图Fig.3 Diagram of penetrating judgment
进行节点穿透判断时,若g(xs)>0,则表示板料节点xs并没有穿透模具单元;若g(xs)<0,则表示板料节点xs已经穿透模具表面进入模具内部.此时,需要将该节点拉回到模具表面,使其成为附着在模具表面的固定点.
经过几何处理后,所有穿透模具表面的节点都被拉回到模具表面.但是,实际上并非所有节点都附着在模具主表面,此时,需要进一步确定节点状态.针对拉回到模具表面的节点,根据投影前后的位置变化来计算相应的节点内力、内力方向与投影单元外法线的夹角.如果该夹角小于等于90°,则说明节点受到向外的拉力,将其释放为自由节点,并添加到非接触区节点集合中;否则,该节点仍然为附着在模具表面的固定点.
2.3 平衡方程的建立与求解
因为接触区构形可以根据接触状态和模具形状来确定,所以本文采用基于预应力膜单元建立平衡方程的方法来计算非接触区构形.
表示中性面的平面应变,其中:
预应力膜单元在变形过程中的几何关系为
ε=εL+εNL=Ba=(BL+BNL)a
(2)
式中:ε为应变;εL、εNL分别为线性应变和非线性应变;B为应变与位移的转换矩阵;BL、BNL分别为线性应变和非线性应变分析的矩阵项,前者与a无关,后者是a的函数.
尽管预应力膜单元在变形过程中的位移和挠度都较大,但由于结构的应变不大,所以单元具有大位移、小应变的特点[12].根据这一特点,假设材料的应力-应变关系满足如下线弹性关系:
σ=Dε+σ0
(3)
式中:D为弹性矩阵,其与材料属性相关;σ0为膜单元的预应力.
在单元所在的局部坐标系下,根据几何关系和本构关系,利用虚功原理建立如下关系式:
(4)
式中:V为单元的体积;a*和ε*分别为虚位移和虚应变;f为局部坐标系下单元所受外力,在使用预应力膜单元进行有限元计算的过程中,f=0.
由虚位移a*的任意性所得非线性问题的平衡方程为
(5)
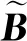
本文采用Newton-Raphson迭代法进行求解,即
(6)
式中:ω为迭代收敛松弛因子;an为第n迭代步的位移向量;Δan为第n迭代步的位移增量,n=0,1,2,…;Ψ(an)为an的函数;KT为切线刚度矩阵,且
KT=K0+Kσ+KNL
K0为小位移的线性刚度矩阵,与BL和D有关,KNL为大位移刚度矩阵,与BL、BNL及D有关,Kσ为几何刚度矩阵,与应力σ及形函数对坐标的偏导数有关.
在迭代过程中,采用位移收敛准则与最大迭代次数相结合的方法进行收敛判断.若节点位移范数满足位移收敛准则,则求解结束;若迭代次数大于最大迭代次数时仍未满足位移收敛准则,则认为迭代发散,求解不成功,此时,需要采用缩小步长的方法重新构造中间构形.
3 实例验证
本文以NumiSheet 2005’标准考题的汽车前翼子板零件为例来说明所提算法的有效性.其中,初始板料几何尺寸如图4(a)所示.图4(b)为冲压初始时刻板料与模具的装配图.其中,上层为凸模,中间为压边圈和板料,下层为凹模.板料的初始厚度为 0.7 mm,包括 1 313 个节点和 2 468 个三角形单元,所选板料的弹性模量为210 GPa,泊松比为 0.3,密度为 7.8 g/cm3,摩擦系数为 0.2,其单向拉伸的应力与应变关系为σ=545.0(0.004+ε)0.263,凸模的总行程为 262.30 mm.
为了验证本文提出的算法的有效性,将本文算法集成到自主研发的基于大步长静力隐式有限元模拟分析软件QuickForm中,并将计算结果与显示动力算法的模拟分析软件LS-DYNA的模拟结果进行对比.取零件的截面线A-A′(如图5所示),并对比在A-A′ 线位置的中间构形形状.
由于重力和压边圈的作用,使得拉延深度小于150 mm的中间构形形状与初始重力作用的中间构形形状相似,所以本文只比较拉延深度为170和200 mm时中间构形的计算结果.其中:当拉延深度为170 mm时,LS-DYNA软件中含 14 856 个节点和 26 732 个三角形单元,总面积为 1.015 m2;QuickForm软件中含 6 842 个节点和 12 464 个三角形单元,总面积为 1.012 m2,两者预测的总面积相当接近,相对误差为3%.拉延深度为200时,LS-DYNA软件和QuickForm软件计算的单元总面积分别为 1.029 和 1.025 m2,相对误差为4%.沿着截面线A-A′比较拉延深度为170和200 mm时两种软件计算的xOz平面的中间构形形状如图6所示.由图6可见,在不同的拉延深度下,两种算法预测的中间构形形状很接近,即两种算法均能够合理地计算当前拉延深度下零件的成形形状,从而验证了采用预应力膜单元构造中间构形方法的有效性.图7示出了拉延深度为200 mm时两种软件计算的中间构形板料厚度分布情况.可以看出,两者的厚度分布趋势相近,板料的减薄区域和增厚区域相一致.

图4 前翼子板尺寸及其与模具装配图Fig.4 Front fender module and assembly drawing

图5 截面线示意图Fig.5 Diagram of section line
在英特尔酷睿5处理器、频率 3.20 GHz、内存8 GB 的计算机上进行计算,使用QuickForm软件进行冲压成形模拟,耗时为 90.24 s,在合模状态下的成形零件包含 11 768 个节点和 21 983 个三角形单元.同时,在相同的计算机上,利用LS-DYNA软件进行冲压成形模拟,耗时为 426.68 s,图8所示为采用两种软件计算的成形结果.由图8可以看出,两者的厚度分布趋势一致,但LS-DYNA软件比QuickForm软件具有更多的板料厚度分布层数,这是由于前者采用了加密级数较多的网格的缘故.图9示出了采用两种软件在合模状态下计算的截面线A-A′上的厚度分布情况.可以看出,采用基于大步长静力隐式有限元算法(软件QuickForm)与采用显式动力算法(软件LS-DYNA)所获厚度分布曲线吻合,两者在增厚区域和减薄区域的厚度分布基本一致.
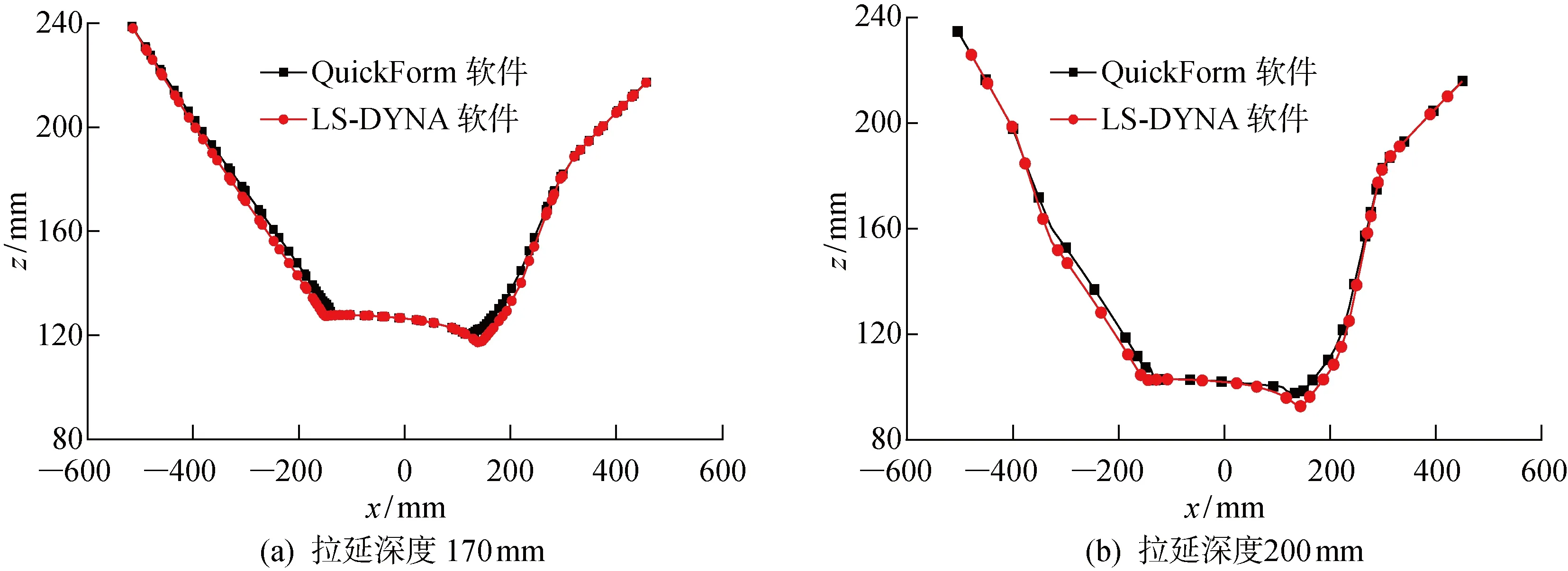
图6 两种拉延深度下中间构形的截面线对比Fig.6 Comparison of section lines at 170 and 200 mm drawing depth
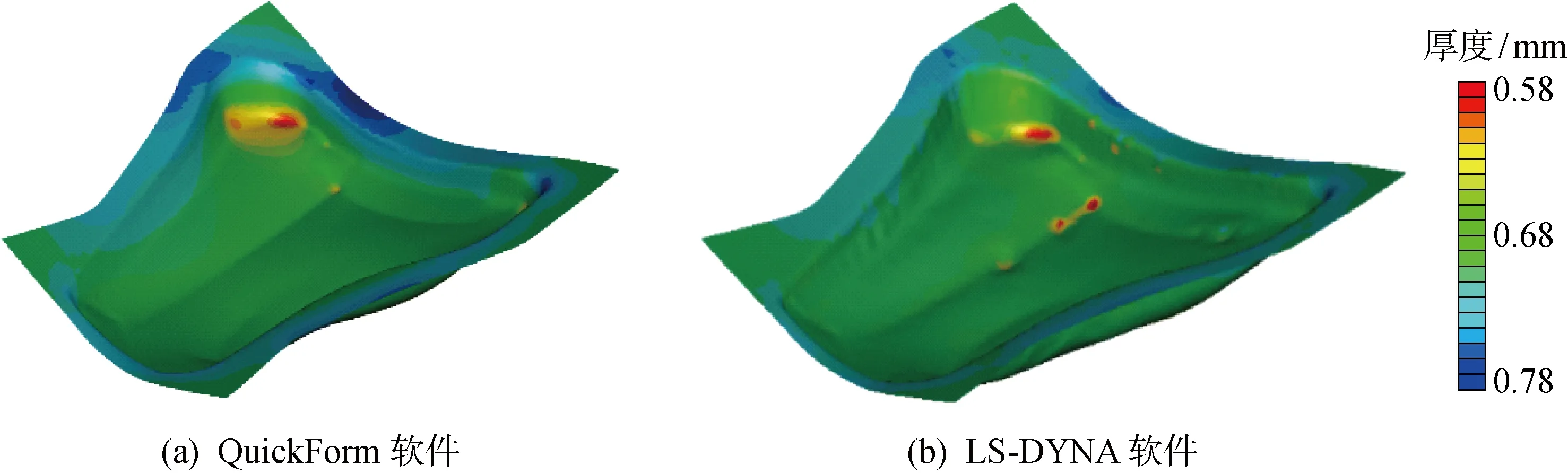
图7 拉延深度200 mm时中间构形板料的厚度分布情况Fig.7 Distribution of thickness in 200 mm drawing depth
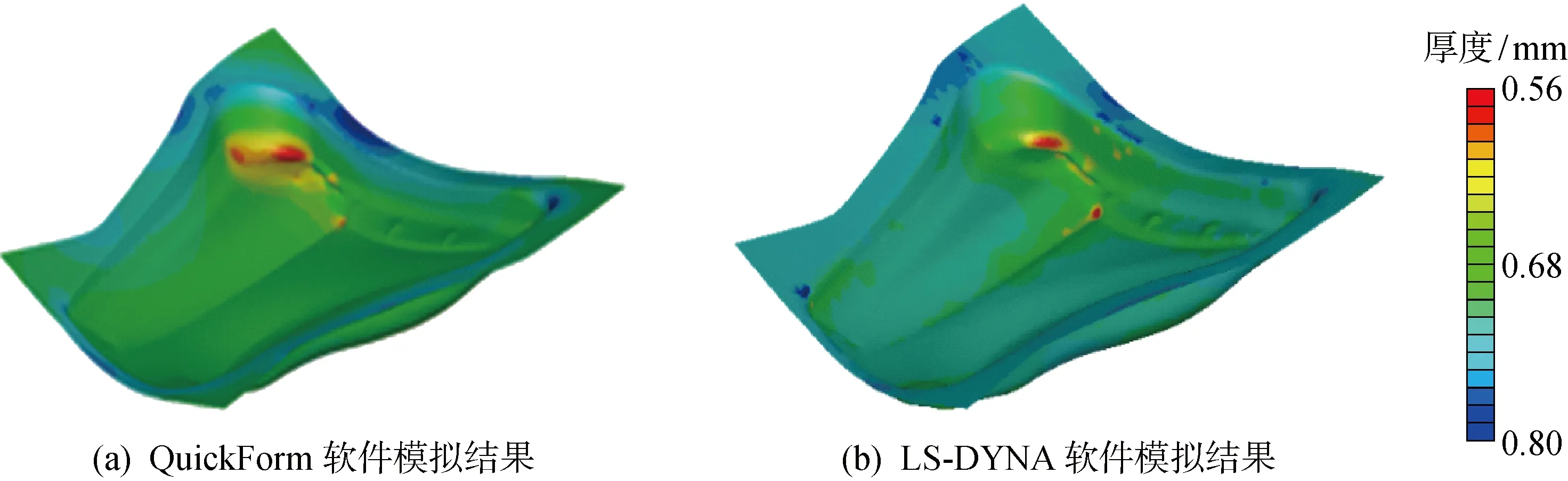
图8 合模状态下成形板料的厚度分布情况Fig.8 Distribution of thickness in clamping status
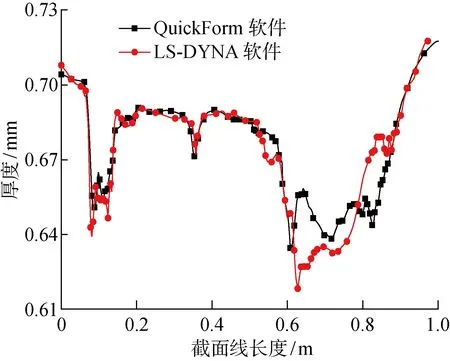
图9 合模状态下截面线A-A′上的厚度分布情况Fig.9 Distributions of thickness with section line A-A′ in clamping status
4 结论
(1) 对于金属薄板成形,采用预应力膜单元的方法能够快速准确地得出基于大步长静力隐式有限元法的板料成形的中间构形.
(2) 所构造的中间构形可作为板料成形快速模拟中拉伸变形计算过程的滑移约束面,使用基于大步长静力隐式有限元算法计算滑移约束面的拉伸变形,可以得到合理的成形模拟结果.

