儿童孤独症的高秩矩阵填充模型与方法
李元超, 陈 峰
(上海交通大学 工业工程与管理系, 上海 200240)
准确的儿童孤独症的影响因素分析对孤独症的早期发现与诊疗具有重要的作用.儿童孤独症(ASD)是广泛性发育障碍的一种亚型,以男性多见,男女比例约为6∶1,起病于婴幼儿期,主要表现为不同程度的言语发育障碍、人际交往障碍、兴趣狭窄和行为方式刻板[1].孤独症的病因目前尚不明确,认为可能与遗传因素和后天因素都相关.又因为孤独症对患儿和患儿家庭的危害较大,所以孤独症的早期诊断显得特别重要.清晰准确地了解孤独症的影响因素可以有效地辅助孤独症的诊断,在孤独症的实际诊疗过程中发挥重要的作用,而临床数据中存在着大量的数据缺失现象.一般而言,认为10%~20%的数据缺失量即会对统计结果造成影响,使之偏离实际情况.针对数据缺失现象,统计学家提出了很多填补缺失值的算法,如多重填补(MI),随机森林(RF),最大期望(EM)等.
矩阵填充(MC)方法是目前解决数据缺失的有效方法,由压缩感知发展而来.所谓压缩感知,指的是利用信号的稀疏特性,在远远小于奈奎斯特(Nyquist)采样率的条件下,用随机采样获取信号的离散样本,然后通过非线性算法完美重建信号.之后,Candès等[2]将压缩感知的原理拓展到二维层面,使得原本的向量重建变为对矩阵中缺失元素的填补,并且称其为矩阵填充.矩阵填充在处理大规模数据的表现方面尤其突出,时间复杂性低且精度高.特别是在处理非结构化数据方面,如图形重建、数字识别和图形压缩等,矩阵填充方法表现出了极大的优势,而且在缺失类型为非随机缺失时,矩阵填充也表现良好.
近年来矩阵填充的新方法不断被提出,原有方法的改进报道也很常见.常用的低秩矩阵填充方法有SVT (Singular Value Thresholding)算法、APGL (Accelerated Proximal Gradient Linesearch-like)算法、IALM(Inexact Augmented Lagrange Multiplier)算法等. 许多新的正则化方式被应用到矩阵填充的凸优化建模中,包括交替最小化、交替最小二乘法和截断核范数等.Xu等[3]将交替方向算法应用到非负矩阵填充中,Recht 等[4]提出了利用平行随机梯度下降法求解大规模矩阵填充的方法.
矩阵填充的应用方向广泛,主要有协同滤波、系统识别、传感器网络和图像处理等方面.经典的Netflix问题就是一个协同滤波矩阵填充问题.根据Netflix问题,发展出了各种推荐系统的用户喜好预测问题.曾广翔[5]进行了面向推荐系统的矩阵填充算法研究.Yeganli等[6]将SVT算法应用于图形重建的过程中,有效地恢复了损坏图形中的纹理部分.Li等[7]利用低秩矩阵填充进行了图形的修复,提出了一种鲁棒性较好的算法.Ji等[8]研究了鲁棒视频去噪,提出基于矩阵填充的视频块的去噪算法,结果显著优于其他去噪算法.在医学上,矩阵填充方法被广泛应用于医学影像处理方面,主要用于提取磁共振的影像的特征,去除影像中的噪声以及修复影像[9].
在待填充矩阵稀疏度低的情况下,低秩矩阵的填充效率低.这里稀疏度指矩阵中零元素占总元素的比例.而在日常应用中,待填充矩阵的稀疏性往往不够强烈,此时低秩矩阵填充的算法就变得十分迟钝,表现难以令人满意.针对这种情况,统计学家提出了高秩矩阵填充的概念.高秩矩阵填充采用子空间聚类相关的思路.认为数据来自k个不同的未知线性空间,任务是将数据分别归类到自己所属的子空间中.近年来,许多高维数据背景下的子空间聚类算法被提出.Elhamifar[10]将矩阵的自我表示模型用于高秩矩阵填充.Fan等[11]将交替方向乘子(ADMM)应用于一般的矩阵填充,并且解决了若干典型图像修复问题和子空间聚类问题,得到了令人满意的效果.
本文将ADMM算法应用于矩阵填充,在现有的高秩矩阵填充的成果基础上,提出了一种考虑待填充矩阵中各因素的重要性的高秩矩阵填充(HRMC)算法.其创新性在于结合矩阵填充的特征,根据数据中各要素的重要性在问题建模时赋予不同的权重参数,提高了算法的效率,在解决高秩矩阵填充问题方法表现较为突出.在数值实验部分采用了生成的测试数据与实际孤独症就诊数据,算法精度均表现优秀,填充结果合乎预期.
1 HRMC算法介绍
矩阵填充问题的一般描述如下:
(1)
式中:X为待恢复矩阵;M为X中已知元素的集合,且i,j∈Ω,Ω为矩阵中已知元素的下标集合.但是,该问题为NP-hard,且时间复杂性为指数[2],故求解起来十分困难.此时,Candès等[2]指出可以通过求解原问题的近似问题来求解:
(2)
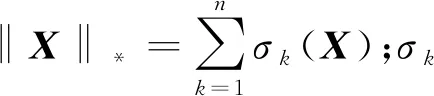
m≥Gn6/5rlgn
(3)
式中:r为矩阵的秩.但是,这种矩阵填充的方法仅仅适用于低秩矩阵的填充,而在日常的应用中,往往会遇到需要恢复高秩矩阵甚至满秩矩阵的情况.通常而言,高秩矩阵填充往往与子空间聚类(SSC)有关,所谓子空间聚类,指有向量x1,x2,…,xn∈Rn,可以被聚类为最多k个子空间.SSC的一般描述如下:
(4)
式中:C为矩阵X的自我表示矩阵,将矩阵X表示成X本身的列的线性组合;E为误差;l为范数,可根据实际问题取某一个特定的范数;λ为由原数据的噪声情况确定,原数据噪声特别大时,λ取比较小的值,反之则取较大的值.
本文结合矩阵填充的思路,利用ADMM算法来实现.ADMM算法通过求解一系列结构相似的子问题来优化未知变量和参数[12].ADMM算法的一般描述如下:
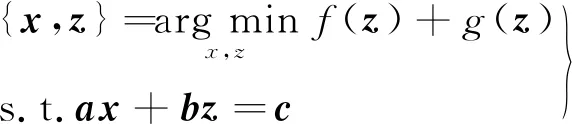
(5)
先求得其增广拉格朗日乘子函数:
Lμ(x,z,y)=f(x)+g(z)+yT(ax+bz-c)+
(6)
然后进行迭代更新,并且重复更新过程,直到整个算法收敛为止.
因为矩阵是不完整的,所以要解决的问题较SSC的研究问题增加了一个约束条件.在实际应用中很难知道待填充的矩阵的秩,故引入了参数αp和λ.其中:αp影响填充矩阵的秩,对较高秩的待填充矩阵,αp应该取比较小的值,反之则取一个较大的值.一般而言,待研究的结构化数据构成的目标矩阵中往往存在关键因素和非关键因素,为了提高算法的运行速度和效率,对关键因素与非关键因素分别赋权值.如此可以使算法将更多资源投入关键因素的缺失项填充过程中,提升效率.注意到约束X=XC+E中,对于不确定的X和C,它是非凸的,而对每一个确定的X和C来说,该约束都是凸的,如此则可用ADMM算法求解.
本文研究的高秩矩阵填充整个问题描述如下:
(7)
为了方便用ADMM求解,式(7)可以表示为
(8)
式中:Y和A均为辅助矩阵;Yp为原矩阵中对应权值αp的因素的集合.增广拉格朗日乘子函数
Lμ=‖C‖l+∑αp‖Yp‖*+λ‖E‖l+
(9)


图1 HRMC算法流程Fig.1 HRMC algorithm process
输入:原始矩阵X,矩阵中已知值M,参数αp和λ.
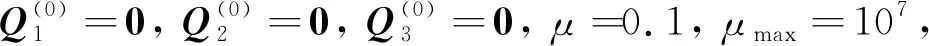
当算法未收敛且k (1) 更新A(k+1),即 (10) (2) 更新C(k+1),即 (11) (3) 更新X(k+1),即 (12) (4) 更新Y(k+1),即 Y(k+1)=arg minα‖Y(k)‖*+ (13) 此时Y为Yp的集合. (5) 更新E(k+1),即 E(k+1)=arg minλ‖E(k)‖*+ (14) (6) 更新乘子: (15) (7) 更新参数: μ=min(ρμ,μmax) (16) ADMM的收敛性已被Stephen Boyd等人证明,且本文在实际求解中,算法均可正常收敛. 在上面的算法描述中,各个迭代步骤都有相似的表达形式.本文可以通过如下方法求A(k+1).即 (17) 同理,在步骤(2)中,C(k+1)的求法是: (18) 式中:Φτ(*)是一个近邻收缩阈值算子[13],其具体定义为 Φτ(ω)=max{|ω|-τ,0}sgn(ω) (19) 式中:sgn(*)为符号函数. 步骤(3)中, (20) 步骤(4)中, (21) 式中:Θ为奇异值阈值算子[14]. 步骤(5)中,E(k+1)求法比较特殊,因为根据不同的应用背景,E的范数可以取不同类型,本文取 2.1 范数,具体的计算方法为 (22) 本文利用了人工生成的测试数据和来自上海市精神卫生中心孤独症门诊的患儿就诊数据进行案例分析.在中国,孤独症患者的数据十分珍贵.因孤独症未得到社会和家庭的足够重视,前来就诊的患儿较少,而且患儿家长在录入基本信息和填写有关量表的时候,由于自身的文化程度或其他原因,往往会有漏填、错填的现象出现,故原始数据中有不少缺失项需要处理.又因数据珍贵,若删除缺失观测,原来的患者分布统计会有较大偏差,而且孤独症各个量表的得分,患者的基本情况各项相关性较弱,故整个数据矩阵的秩较高. 数值实验流程:首先采用生成的测试矩阵测试;然后利用实际的孤独症数据,抽取有代表性的无缺失样本进行测试,并且与常用的参数化填补方式和低秩矩阵填充算法做对比;最后利用全部的实际数据进行矩阵填充实验,观察算法的效率和填充是否合理. 矩阵填充的误差可以表示为 (23) 实验结果如表2所示.表中:rMC为矩阵填充的秩;EMC为矩阵填充误差. 表1 测试矩阵配置Tab.1 Parameters of test matrix 表2 测试矩阵填充情况Tab.2 Result of matrix completion 由表2可以看出,随机生成的测试数据实验结果较好,可以正常收敛,且矩阵填充误差均在可接受范围内.该算法在不同的缺失率下均可使填充后矩阵的秩与原矩阵相等.在随机缺失的前提下,δ分别为 0.25 和 0.5 时基本可以正常填充,δ到达 0.75 时填充效果就有了明显的下降.这与低秩矩阵填充的经验不符.原因是低秩矩阵中有效的元素本身较少,大部分元素均与有效元素相关,即使是高度缺失的矩阵中仍然保留有足够完整恢复原矩阵的信息;而高秩矩阵中本身的有效元素较多,高度缺失的情况下有效信息的损毁过于严重,以至于难以将原矩阵完整恢复. 由表4可见,HRMC在3种算法中表现最为优秀,MI紧随其后,SVT最差,而且随着缺失度增加,矩阵填充误差随之上升.其原因是MI的原理为贝叶斯预测,对矩阵的秩不敏感,而SVT对数据的低秩性和稀疏性要求较高.而MI在缺失模式为NMAR时,填充误差急剧上升,HRMC则不会.这说明MI在处理MAR数据表现较为出色,但无法很好地处理NMAR数据,HRMC则对数据的缺失类型不敏感.若是能寻找一个原始数据的稀疏表示,则一般低秩矩阵填充算法也可应用.综上所述,HRMC在处理实际孤独症数据时表现良好,可以应用到大规模的数据处理中. 表3 实际孤独症数据非随机缺失填充结果Tab.3 Result of practical ASD data completion in NMAR 表4 HRMC与其他算法对比结果Tab.4 Comparison of HRMC and other algorithms 经过必要的数据前处理,原始的孤独症患者数据(包括基本情况和各量表作答情况)被整理为一个499×143的矩阵,矩阵中共有 71 357 个数据,其中 15 497 个数据缺失,缺失度为 21.72%;共有 12 433 个值为0,稀疏度为 17.4%,为稠密矩阵.对该矩阵应用HRMC算法进行矩阵填充,结果很好,缺失值的填充结果均符合各项参数的取值范围,而且速度极快,大约 1 000 步迭代后即会收敛. 本文研究了高秩矩阵的矩阵填充问题,提出了一种基于ADMM算法的高秩矩阵填充算法(HRMC).该算法利用对偶最小化的方法,使得矩阵填充在矩阵本身的秩比较高(甚至满秩),矩阵中的无效元素比较少的时候仍然能以较高的概率恢复原矩阵.本文利用生成的测试数据和截取的实际孤独症数据进行测试,并且将HRMC与一般的参数化方法和低秩矩阵填充方法的表现做对比,结果是HRMC的精确度要显著优于其他算法.不足之处在于全部实际孤独症数据的填充由于原始数据的缺失,故无法精确衡量填充结果.另外,HRMC算法对数据归一化要求高,若数据的各个参数取值波动巨大时,该算法收敛速度较慢.HRMC算法不仅在医疗数据的填补方面,在图形修复、模式识别等领域应该也有不错的表现和广阔的应用前景.
2 数值实验
2.1 测试数据填充实验
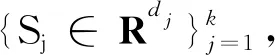
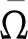


2.2 实际孤独症数据子样本填充

2.3 实证分析
3 结语

