聚焦数学思维 打造有效课堂

王诺

摘要：提高学生数学思维能力，是培养数学核心素养的重要内容。本文结合具体教学案例，从纠正思维方式、唤醒思维活力、打破思维习惯等方面入手，对培养学生良好的数学思维品质进行了探究分析。

关键词：数学思维;“融错”教学;想象;合理设问

中图分类号：G623.5文献标识码：A     文章编号：1992-7711（2019）09-085-2

数学思维是指在数学活动中的思维，是人脑和数学对象交互作用并按照一定思维规律认识数学内容的内在理性活动。数学学习过程不仅是数学知识的积累和数学方法的运用，更是不断强化数学思维品质的过程。笔者发现，学生的数学思维可通过有意识地强化训练，得到不同程度的提高。针对这一观点，笔者现对下列教学案例进行分析探讨。

一、善于“融错”，纠正数学思维方式

“融错教育”，即通过有效的教学活动把学生的错误融化掉，在不断的交流、思考、修改、完善等过程中，不断提升学生的思维能力。例如，苏教版五年级上册期末复习中有一道练习题：2018年4月1日是星期日，这个月上课多少天？休息多少天？

学生作业中有的用表格列出，有的模仿日历的形式列举，笔者还发现了这样的答案：30÷7=4（周）……2（天），休息：2×4=8（天），上课：30-8=22（天）。笔者组织学生对这样的解答方式进行了讨论交流。

师：这样解题对吗？

生1：对的，这个月有4个星期，每个星期有两天休息，所以休息8天。

生2：不对，他没有考虑4月1日是星期几的情况。如果4周余下的两天还是星期六和星期天，就不是休息8天了。

生3：除去4月1日是星期日，4月还有29天，再除以7看有几周，我是这样列算式的：（30-1）÷7=4（周）……1（天），余下的这一天是星期一，那么总的上课天数是4×5+1=21（天）。休息的天数是四周中的星期六、星期日和4月1日的星期日，算式是4×2+1=9（天）。我认为投影的做法不正确。

师：第3位同学的做法，大家明白了吗？

教师及时出示一一列举后的日历情况，帮助学生理解。

生：明白。

师：那最初投影的答案对吗？刚刚你们明白先减1天的方法，就是每个周期从星期一开始计算。那直接用30除以4的情况呢？

生：老师，我明白了。直接用30除以4就是每个周期从星期日开始考虑，星期日到下一周的星期六是7天，有四个周期，30÷7=4（周）……2（天）。第五个周期又从星期日開始数，所以余下的两天分别是星期日和星期一。所以休息时间就是4×2+1=9（天），上课时间就是4×5+1=21（天）。

全班响起热烈的掌声。学生一致认为最初投影的方法是不对的，而且知道错到哪里，怎样订正。

教师再次出示星期日为周期之首的列举情况，学生体会这种方法的合理性。

生：老师，我觉得这个答案是有问题的，4月有个清明节小长假，也是休息。

师：这个问题提得真好，练习题中应该附加一个条件，即“不考虑小长假的情况”。

生：老师，之前遇到大图形裁剪小图形最多可以有多少个时，你告诉我们要注意附加条件，不考虑能拼接的情况。

上述这种“融错”方式，可以使学生经历思路的碰撞，有意识地训练学生的逻辑思维，让学生自然而然地纠正错误的思维方式，形成有条有理、有根有据的解题思路。

二、巧妙想象，唤醒数学思维活力

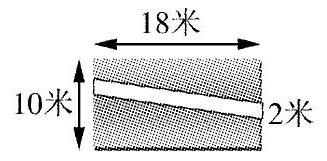
教师采用“引导想象”的策略，可以使学生观察到隐蔽的、不易觉察的关系，使复杂的问题简单化，从而进一步发展学生思维的灵活性和创造性。例如：苏教版五年级上册教学组合图形的面积之后有这样一道练习题：如图，一块长方形草地，长方形的长是18米，宽是10米，中间铺了一条石子路。问草地的面积是多少平方米？

师：谁来说说解题思路？

生：可以用长方形的面积减中间小路的面积，就是草地的面积。

师：中间小路的面积可以计算出来吗？

生：可以，小路是平行四边形。底是2米，高和长方形的长相等是18米，底乘高是36平方米。

师：思路真清晰！但你能直接求出草地的面积吗？

学生面面相觑，眼中流露出困惑。

师：有什么疑问吗？

生：直接求草地的面积就是直接求两个梯形的面积，可梯形的上底和下底都不知道。

师：那我们想象一下，把下面的梯形向上平移。下面梯形的面积会变化吗，为什么？

生：不变，因为平移不改变图形的大小。

师：那我们接着想象，如果下面的梯形继续向上平移……

生：老师，我知道了，上下两个梯形可以凑到一起，拼成一个新的长方形。

学生想象后，课件动画演示下面的梯形向上平移的过程和结果。

师：新的长方形的长和宽知道吗？

生：拼成的长方形的长和原来一样，宽是10米减2米。

师：宽为什么是原来的减2？

生：因为小路的底是2米，下面的梯形向上平移了2米，所以新的长方形的宽就减少了2米。

师：现在老师把这道题改一改，你会做吗？

如图，一块长方形草地，长方形的长是18米，宽是10米，中间有两条路，一条是长方形，一条是平行四边形。问草地的面积是多少平方米？

生1：可以把下面两块草坪向上移，右面的两块草坪向左移，这样四块草坪合起来后又是一个新的长方形。

生2：新的长就是15米，新的宽就是8米。

生3：老师，如果不这样想象，以前的方法也可以。用长方形的面积减去两条小路的面积。但是两条小路有重叠的地方，这部分减了两遍，需要最后再加上小路重叠部分的面积。

生4：老师，这种方法太麻烦了，还是把草坪想象成一个新的长方形，再计算面积。

就这样，通过引导学生进行上述脑海浮现，使面积计算与空间想象发生关联，数据计算也有了发展空间观念的价值。同时，例1和例2属于同类型、同结构的题目，但例2难度有所增加，处于学生的最近发展区。教师有意将两个习题设置在一起，通过巧妙引导、递进练习，让学生再次经历想象的过程，使学生在交流、想象中进行思维的碰撞，并从中灵活地选择算法。这样的教学活动对于提升学生的思维品质是有益的。

总之，要想发展学生的核心素养，就必须在提升学生的数学思维能力上下工夫。在数学教学过程中，教师要始终关注学生的思维起点，挖掘学生的思维深度，扩展思维广度，在课堂讨论交流和解决问题中慢慢培养学生良好的思维品质。