络合铁法湿式脱硫再生反应动力学

向言 俞英 黄海燕

中国石油大学(北京)理学院

硫化氢(H2S)是炼油行业的有害物质之一，是一种无色、有毒气体。当pH值>7时，H2S在水中主要以HS-形式存在，这将对管道和设备产生腐蚀，造成严重的经济损失[1-2]。工业上脱除H2S的方法较多[3-8]，其中，采用络合铁做催化剂的湿法氧化脱硫方法具有以下优点：①吸收效率高，可使尾气中H2S体积分数低于10×10-6；②可操作性强，且多数脱硫剂可再生；③经济环保。因此，湿法氧化脱硫工艺得到了广泛的应用[9-11]。

在公开报道的文献中，关于络合铁溶液的再生动力学研究较少，尤其是关于再生过程的再生效率及络合亚铁浓度分布模型的报道更为少见。关于络合铁溶液再生动力学的研究，Sada[12]和Demmink[13]等学者均采用建立模型的方式，研究对象主要为EDTA-Fe(Ⅱ)溶液。研究发现，当络合亚铁浓度为0.1 mol/L、pH值为7.0～7.5、T为293～333 K时，EDTA-Fe(Ⅱ)再生过程的活化能为36.0 kJ/mol，反应速率常数k为5.8×104m6/(mol2·s)。陈煜泉等[14]通过实验研究得出当T=298 K、pH值=9.0时，反应速率常数k=147.9 L/(mol·s)。对于反应级数的研究，通常认为再生过程对O2的级数为1，络合亚铁的反应级数则与络合亚铁自身的浓度有关[14-17]。

本研究以EDTA-Fe(Ⅱ)溶液为再生液，采用静态的气液扩散反应器建立氧化再生反应动力学方程，并以此作为建立模型的基础，通过研究单个气泡中O2含量的变化，估算出不同气液比、再生温度、pH值等条件下再生液中络合亚铁浓度随时间的变化规律，为工业生产及再生反应器的设计提供一定的理论指导。

1 动力学模型建立

再生过程反应方程式见式(Ⅰ)～式(Ⅱ)：

1/2O2(g)+H2O1/2O2(aq)+H2O

(Ⅰ)

1/2O2(aq)+H2O+2EDTA-Fe(Ⅱ)→

2EDTA-Fe(Ⅲ)+2OH-(Ⅱ)

实验研究发现，气相中O2含量、再生液中EDTA-Fe(Ⅱ)浓度和再生液pH值对再生过程的影响较为显著。因此，定义该反应单位面积动力学方程，见式(1)：

(1)

由式(Ⅱ)可知：

rS(O2)=rS[EDTA-Fe(Ⅱ)]/4

(2)

本研究采用电极电势的方法分别探究了各个因素对表观再生速率的影响，通过实验可确定再生反应对于各个因素的反应级数、再生活化能和速率常数实验装置示意图见图1。

在真实的再生过程中，含有O2的混合气体从再生塔底部形成均匀连续的气泡进入再生液中，络合亚铁被持续消耗，本模型中以络合亚铁摩尔分数每减少5%分段进行独立计算，该时间段内认为络合亚铁摩尔分数不变。各阶段参与反应的气泡总个数为每个时间段进气总量与单个气泡体积的比值。如果能确定单个气泡气液界面被反应掉的络合亚铁的量，即可求得络合亚铁摩尔分数每消耗5%所需要的反应时间。

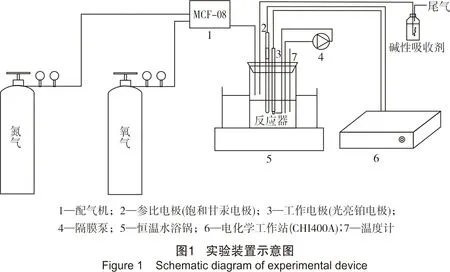
若以单个气泡为研究对象，在气泡上升的过程中，气泡内部的O2通过传质作用扩散到液膜层，与再生液中的络合亚铁发生反应，假设化学反应速率远大于扩散速率，那么被反应的O2量等于从气相扩散到液相中的量。考虑到体系压力不高，温度较低，可认为混合气体遵循理想气体状态方程。则进气口气泡中的O2物质的量为：

n0=pV/(RT)，p=p0+ρlgh

(3)

由式(1)和(2)可知，在dt时间段内气泡中O2摩尔分数变化为：

dn=rS·AS·dt/4

(4)

将式(3)代入可得，

(5)

考虑到络合亚铁浓度、O2含量、体系中氢离子浓度、气泡体积和气泡所处高度均随时间而不断发生变化，若根据式(5)通过积分的方法求气泡中O2体积分数的变化十分困难，故本研究将运用分段的方法达到快速计算的目的。同时，基于以下假设进行理论模型的计算：

(1)在气液比不是很大时，气泡上升过程中始终保持为球形，且气泡内部温度不变。

(2)对于每段的计算，由于nEDTA-Fe(Ⅱ)≫nO2，单程EDTA-Fe(Ⅱ)转化率不高，所以络合亚铁浓度消耗较小，可以认为络合亚铁浓度基本保持不变。

(3)考虑到气泡中O2体积分数较高(约30%)且再生速率较小，则每段气泡内O2体积分数和气泡大小的变化可以忽略不计。

那么气泡经过第1段液柱时间内被络合亚铁消耗的O2物质的量为：

(6)

则第2段进口处气泡中O2物质的量为：

n1=n0-n1'

(7)

第2段O2消耗量为：

(8)

依次计算可知，气泡经过第m段液柱时间内消耗的O2物质的量为：

(9)

第m段出口处气泡中O2物质的量(m+1段进口处气泡中O2物质的量)为：

nm=n(m-1)-nm'

(10)

经历过m段后再生液中EDTA-Fe(Ⅱ)物质的量变化：

(11)

其中，单位表面积反应速率rS可通过式(2)直接计算得到。而气液接触时间(反应时间)t尚不可知，故需进一步确定反应时间t。

以单个气泡为研究对象，上升过程中气泡的运动状态主要受到气泡浮力及来自再生液的阻力影响。气泡的重力可忽略不计，则浮力与阻力的差值将产生1个向上的加速度，所以气泡先做变加速运动；当气泡上升到某一高度时，阻力将与浮力在数值上相近，可以认为气泡做匀速运动，此时，气泡的速度称为上升末速度。则气液反应时间由两部分组成：变加速运动时间和匀速上升时间。

气泡匀速运动阶段所用时间

t1=H/vt

(12)

vt为上升末速度，可由Mendelson经验公式计算得到[18]：

vt=[2σ/(db·ρl)+g·db/2]1/2

(13)

气泡变加速阶段所用时间t2的计算：

气泡产生的浮力

(14)

来自再生液的阻力

(15)

由牛顿第二定律可知，产生的加速度为：

(16)

表1为在30 ℃、pH值=8、cEDTA-Fe(Ⅱ)=0.064 mol/L的条件下再生液和气泡的基本物性，将表1中数据带入可得，

dv/dt=8 205.7-130 853.8CDv2

(17)

当加速度为0时，通过式(13)得到上升末速度带入式(17)得到CD，再对式(17)积分可得，

v=2000/[5357(1+e-87926t)]-1000/5357

(18)

由式(18)可知，气泡变加速至匀速阶段所需时间t2≪0.01 s，而匀速上升时间一般为几秒到十几秒，故相比而言，变加速阶段气泡上升时间是可以忽略不计的，可近似认为气泡形成的瞬间即开始做匀速运动。通过以上推导，气液反应时间可由式(19)计算所得：

t=H/[2σ/(db·ρl)+g·db/2]1/2

(19)

表1 再生液和气泡基本物性Table 1 Properties of regeneration solution and bubble性质密度/(kg·m-3)表面张力/(N·m-1)气泡初始直径/m动力黏度/(Pa·s)脱硫液1 046.830.0321.6×10-3气泡1.250.004 8

2 氧化再生反应动力学参数的确定

2.1 实验方法

再生过程中总铁含量一定，而络合亚铁的量随反应的进行不断减少，EDTA-Fe(Ⅱ)与EDTA-Fe(Ⅲ)物质的量之比减小。假设各离子活度系数不变，由能斯特方程可知：在一定的温度和pH值条件下，溶液电势的变化是由于铁离子的变化引起的。因此，本研究通过电化学工作站(CHI400A)测定溶液的OCPT曲线，再将电极电势带入相应标准曲线可获得cEDTA-Fe(Ⅱ)-t曲线，通过非线性拟合得到c(t)方程，对其微分，即可得到再生速率曲线-dcEDTA-Fe(Ⅱ)/dt-cEDTA-Fe(Ⅱ)，最后代入各自的络合亚铁浓度就能得到相应的表观再生反应速率。

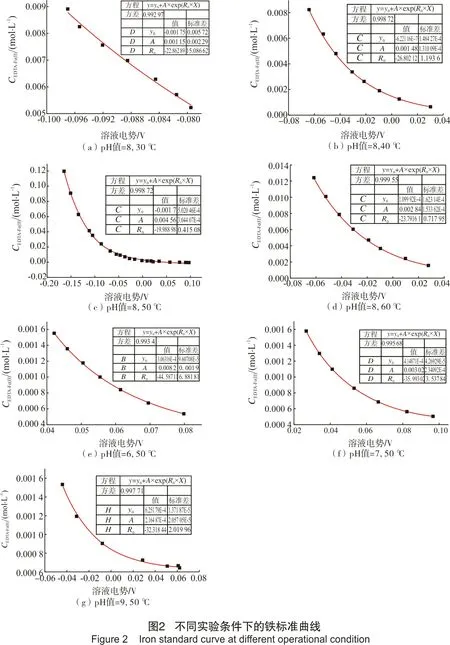
标准曲线的绘制：根据实验需要配置不同络合亚铁浓度的再生液，溶液pH值通过加入磷酸三钠(Na3PO4·12H2O)或磷酸二氢钠(NaH2PO4·2H2O)来调节，再生温度由恒温水浴锅控制。本实验中，光亮铂电极(DJS-1C)作为工作电极，饱和甘汞电极作为参比电极。由电化学工作站测定溶液电势，每隔一段时间取样并记录此时的溶液电势，样品中络合亚铁浓度采用邻二氮菲分光光度法测得[19-20]。通过origin做非线性指数拟合即可得到铁标准曲线(c-E曲线)，本研究分别测量了同一pH值对应不同温度(分别为30 ℃、40 ℃、50 ℃、60 ℃)的4条标准曲线以及50 ℃下对应不同pH值(分别为6、7、9)的3条标准曲线，如图2所示。

2.2 确定对EDTA-Fe(Ⅱ)浓度的反应级数

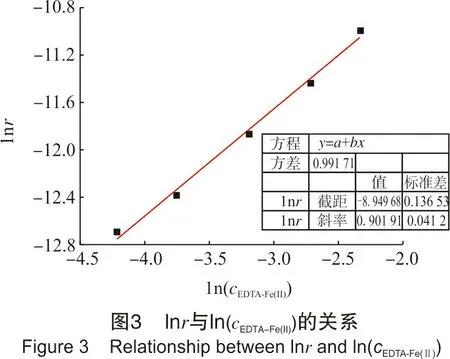
控制总铁浓度约0.25 mol/L，分别配置200 mL络合亚铁浓度分别为0.015 mol/L、0.023 mol/L、0.041 mol/L、0.066 mol/L、0.097 mol/L的5种再生液。通过微型注射泵向体系补充酸，从而维持整个反应过程溶液pH值为8。体系反应温度为50 ℃，待温度稳定后，通入O2体积分数为30%的气体(其余为N2)进行反应，记录OCPT曲线。图3为数据处理结果。从图3可知，亚铁浓度越高，再生过程的表观反应速率越快，该再生反应相对于EDTA-Fe(Ⅱ)浓度的反应级数为0.902。

2.3 确定对O2体积分数反应级数

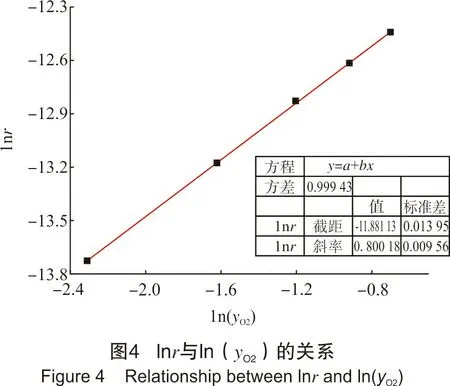
配置总铁浓度约为0.25 mol/L、EDTA-Fe(Ⅱ)浓度为0.021 mol/L、pH值=8的再生液1000 mL，分成5组。再生温度为50 ℃，依次进行O2体积分数分别为10%、20%、30%、40%、50%的再生实验，记录相应的OCPT曲线。图4为数据处理结果。

从图4可以发现，再生过程的表观反应速率随气相中O2体积分数的增加而加快，说明O2体积分数越高，越有利于再生反应的进行，该再生反应对O2体积分数的反应级数为0.8。

2.4 确定对氢离子浓度的反应级数

配置总铁浓度约为0.25 mol/L、EDTA-Fe(Ⅱ)浓度为0.001 5 mol/L、pH值分别为6、7、8、9的再生液各200 mL。设置再生温度为50 ℃，O2体积分数为20%，分别进行再生实验，通过微型注射泵向体系中补充酸，从而控制整个反应过程溶液pH值维持在各自初始值，记录相应的OCPT曲线。图5为数据处理结果。

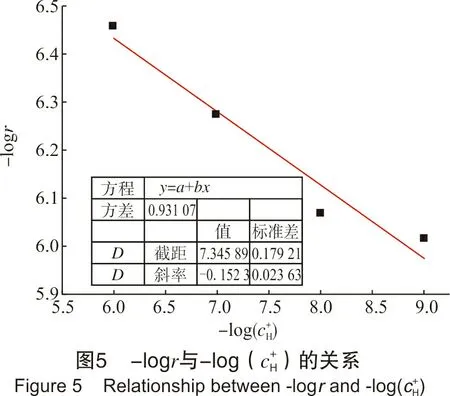
从图5可以发现，再生过程的表观反应速率随溶液中氢离子含量增加而减小，说明氢离子含量高不利于再生反应的进行，该再生反应对氢离子浓度的反应级数为-0.152。

2.5 确定单位表面积速率常数和再生活化能

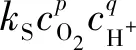
(20)

对式(20)积分可得：

-c0.098/0.098=k'·AS·t/Vl+b

(21)

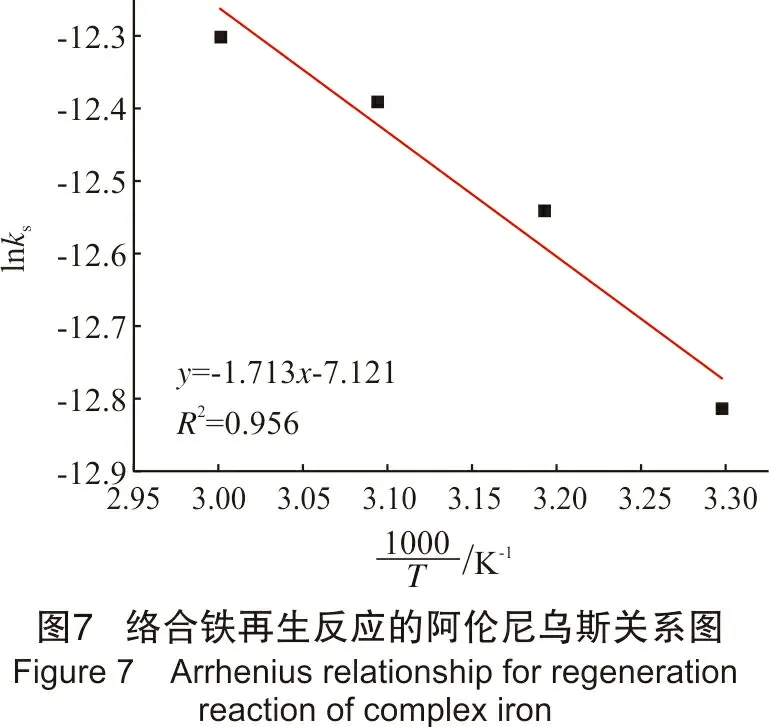
由图6可得出各温度下的单位表面积速率常数。由阿伦尼乌斯方程可知：lnkS=lnk0-Ea/RT

通过图7可估算出再生反应活化能为：

kS=k0e-Ea/RT

(22)

k0=8.082×10-4，Ea=14.24 kJ/mol

3 模型验证

设置混合气的进气流量为30 mL/min，O2体积分数30%，EDTA-Fe(Ⅱ)浓度为0.064 mol/L，pH值为8，再生温度为30 ℃。在再生塔中进行再生实验，将所得实测数据与模型结果进行对比，结果见图8。

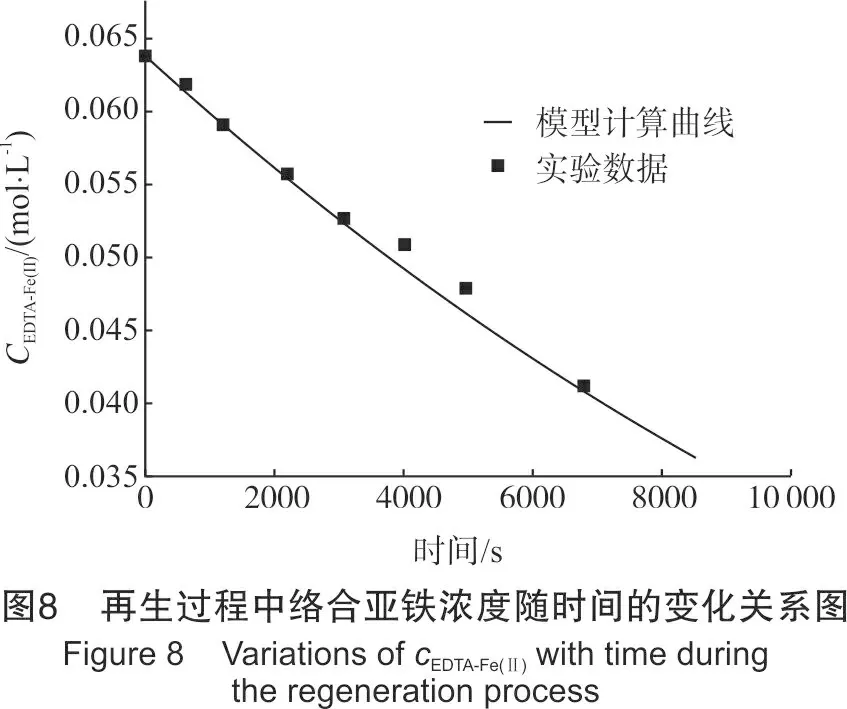
由图8可知，通过理论模型所得EDTA-Fe(Ⅱ)浓度分布与实验数据吻合较好，说明在实验考察范围内，该模型可作为工业生产及反应器设计的理论指导。

4 结论

在研究结果的基础上，总结出以下结论：

(1)络合亚铁与O2的再生反应对于络合亚铁浓度的反应级数为0.902，对于O2体积分数的反应级数为0.8，对氢离子浓度的反应级数为-0.152。

(2)再生反应活化能为14.24 kJ/mol。

(3)结合单位表面积动力学方程推导出的再生动力学模型与实验数据具有较高的吻合度，证明了该模型的可行性。同时，通过该模型可以准确快速地计算出再生过程再生效率及络合亚铁在再生过程中随时间的浓度分布，对工业生产和再生反应器的设计、空气鼓风量和络合剂的补加量等具有一定的理论指导意义。

符号说明

AS：气液接触面积，m2

cO2：气相主体中O2浓度，mol/L

cEDTA-Fe(Ⅱ)：溶液中络合亚铁浓度，mol/L

cH+：溶液中氢离子浓度，mol/L

yO2：气相主体中O2摩尔分数

m:反应物络合亚铁对应的反应级数

p:反应物O2体积分数对应的反应级数

q:氢离子浓度对应的反应级数

CD：阻力系数

db：气泡直径，m

Ea：活化能，kJ/mol

H：气泡距离再生液液面高度，m

n0:气泡中的初始O2物质的量，mol

ρl：再生液密度，kg/m3

ρb：气泡密度，kg/m3

p：气泡受到的压力，Pa

p0：大气压，101 325 Pa

rb：气泡半径，m

R：气体常数，8.314 J/(mol·K)

S：气泡表面积，m2

rS：单位表面积反应速率，mol/(s·m2)

v：气泡上升速度，m/s

V：气泡体积，m3

σ：表面张力，N/m

nm'：气泡通过第m段液柱时间内被络合亚铁消耗掉的O2物质的量，mol

nm：第m+1段液柱入口处的气泡中所含的O2物质的量，mol