感应电动机转子偏心故障诊断方法研究

邵思语

(华南理工大学，广州 510641)

0 引 言

感应电动机因其结构、性能等方面的优势，在众多领域都得到广泛应用。随着现代产业的发展，对感应电机的要求也更加严格，转子偏心故障程度轻时会使电机气隙磁场发生畸变，损坏性能参数指标；程度重时则会使定、转子间相摩擦，有时甚至会烧毁设备乃至发生机毁人亡的重大安全事故。因此，对感应电动机转子偏心故障的诊断与研究具有重大意义。

国内外学者针对电机故障提出许多研究方法：Bashir Mahdi Ebrahimi[1]等提出运用时间步进有限元法对定子电流加以分析，推断是否发生偏心故障；Nandi S[2]等学者提出可通过检测电机振动信号实现转子偏心故障的诊断；Tenhunen A[3]等利用有限元分析法对异步电动机进行不平衡磁拉力的研究；我国的姚大坤[4]等对转子偏心情况时不平衡电磁力展开研究，给出了在最小二乘意义下的非线性函数表达式；中国矿业大学的韩丽[5]等人将电机定子电流、径向振动信号等进行多信息融合，从而诊断故障；孙跃[6]应用基于端部漏磁分析法实现电机偏心故障的诊断；扬州大学的吴桂峰[7]等应用小波—神经网络来分析振动故障。

基于以上文献可知，现代常用于电机故障诊断的方法有：电流分析法诊断；振动诊断；磁分析诊断等。本文主要从定子电流频谱、不平衡磁拉力及振动信号的角度进行研究，由于快速傅里叶变换(以下简称FFT)分析时存在频谱泄漏和栅栏效应[8]，特征会被淹没而难以识别，本文提出改进创新的小波包分析结合FFT信号分析法，更有效地提取电流特征频率；通过理论与有限元仿真分析电机在三种状态下的径向电磁力，得出力波阶次和频率分布的对应特征，同时也为振动分析的特征频率给予理论基础。本文的三种诊断方式对于实际工程应用中都有着一定的实用价值。

1 转子偏心前后磁场分析

1.1 转子偏心故障分类

据几何性质差异，转子偏心可分为两种基本类型：轴向均匀偏心和轴向不均匀偏心即斜偏心(IE)[9]。其中，轴向均匀偏心包含静态偏心(SE)、动态偏心(DE)及混合偏心(ME)。图1为电机偏心模型图。

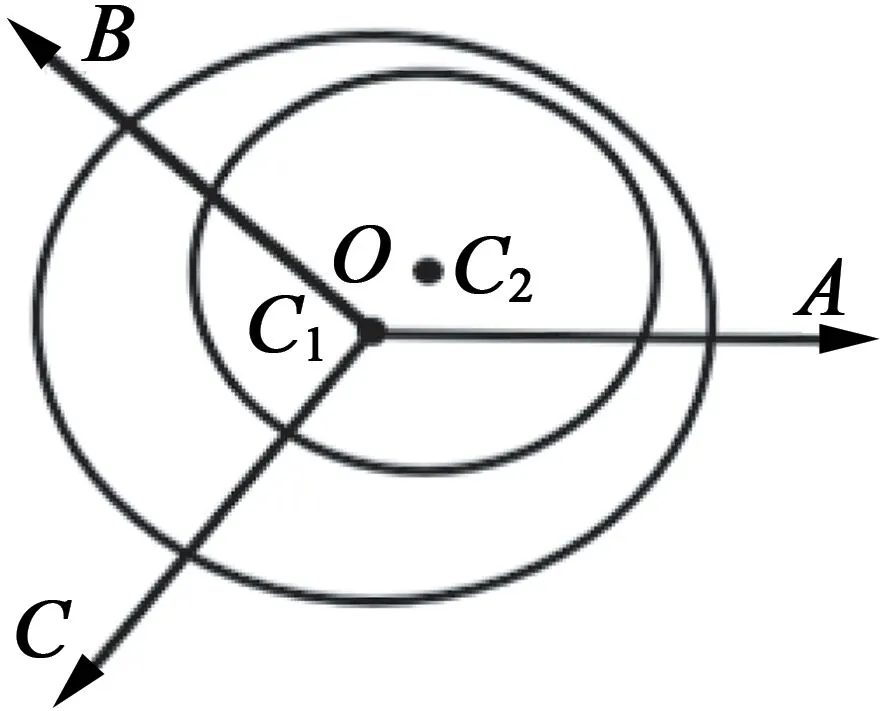
图1 电机偏心模型

电机偏心时，转子轴心C2与定子轴心C1不重合。静态偏心时，电机转轴O位于C2上；动态偏心时，O位于C1上；混合偏心时，O于C1，C2之间。

1.2 转子偏心故障机理

在实际运行中，感应电动机发生的转子故障以断条与转子偏心占较大比例。转子静态偏心是转子以自身为转轴，且与定子不同心，造成偏心时最小气隙位置的具体空间分布基本不变，为空间函数。转子静态偏心产生原因有：电机定子铁心内径椭圆度，转子定位不够准确，定转子不同心，或是安装及配置不正确等。转子动态偏心是转子以定子轴心为转轴，使最小气隙位置随转子同步移动，即气隙最小位置随转子旋转进行移动，为时空函数。转子动态偏心产生原因有:转轴弯曲扰度，轴颈椭圆，安装不同心，转子铁心不圆，临界转速时的机械振动，轴承损坏传动等。

1.3 气隙磁场分析

1.3.1 定、转子磁势

定子绕组三相对称分布，其气隙合成磁势：

(1)

式中：fp(θ,t)为主波合成磁势；fv(θ,t)，fμ(θ,t)分别为定、转子绕组产生的谐波磁势。

1.3.2 混合偏心气隙磁导

混合偏心故障时，电机定、转子的气隙长度分布不均匀。忽略齿槽效应对感应电动机的影响[10]，给出静偏心、动偏心、混合偏心三类情况的气隙长度，分别如下：

g(θ)=g0(1-δscosθ)

(2)

g(θ,t)=g0[1-δdcos(ωrt-θ)]

(3)

g(θ,t)=g0[1-δscosθ-δdcos(θ-ωrt)]

(4)

式中：g0为均匀气隙长度(不偏心)；δs，δd为静态、动态偏心度。混合状态为叠加式(2)、式(3)两种基本状态时的气隙长。考虑存在混合偏心情况时气隙磁导，并进行傅里叶级数分解，得：

(5)

傅里叶级数系数：

(6)

通常情况下，电机气隙磁导的解析式可进行如下简化(气隙偏心e很小，忽略高阶磁导分量)：

Λ=Λ0+Λ1cosθ

(7)

1.3.3 气隙磁场

电机正常工况下，由磁场理论，考虑各种不同情况磁导因素影响下的总磁导与式(1)相乘，可得相应的气隙磁密，磁通密度为时空函数。电机气隙磁密瞬时值b(θ,t)表达式可参考文献[11]，本文不再赘述。当气隙混合偏心时，气隙磁密表达式除了含有电机正常运行情况时的磁密外，还有由存在气隙偏心所引入的谐波磁密：

(8)

式(8)中：静偏心时，ωr=0；动偏心时，ωr≠0；混合偏心时，对应引入的谐波磁密为前两者之和。混合偏心引入的各部分气隙磁密谐波分量如表1所示。序号1～6是电机混合偏心引入的磁密谐波，其中序号1～3的谐波分量是由静偏心引起；序号4～6的谐波分量是由动偏心引起，f1为基波频率，fr为转子旋转频率。

表1 混合偏心状态下引入的磁密谐波

假设感应电动机定子磁势变换按正弦规律，那么定子电流线密度J可表示如下：

Js(θ,t)=Jssin(ωt-pθ)

(9)

式中：Js为定子线电流密度幅值；ω为定子供电电网频率；p为电机极对数。

利用定子磁势波与气隙磁导二者乘积形式进行表达的感应电机气隙磁场：

(10)

2 偏心故障诊断方法建立及仿真实验

具体电机诊断过程如图2所示，可通过传感器等方式从电机中采集不同类型信号信息，再通过有效方式进行故障特征提取，并与判别特征进行对比分析，最终实现故障类型及危害严重程度等方面的诊断，确定应对措施和实施方案。

图2感应电动机故障诊断过程

2.1 定子电流频谱法

当感应电动机出现转子偏心故障时，气隙磁势场发生畸变，相应产生除基波峰值以外的其它峰值影响定子电流频谱，即会存在一些特定的故障特征频率。通过采集定子电流信号并进行频谱分析便可实现诊断故障[12]。对于转子偏心故障的定子电流特征频率已有大量文献研究，本文将结论进行总结整理后得到公式如下：

(1) 高频段电流故障特征频率

转子静态偏心(nd=0)：

fec=[Z2(1-s)/p±1]f1

(11)

转子动态偏心(nd=1)：

fec=[(Z2±1)(1-s)/p±1]f1

(12)

(2) 低频段电流故障特征频率：

fec=f1±mfr

(13)

式中：fec为频率分量(气隙偏心的函数)；Z2为转子槽数；s为转差率；nd为动态偏心级数；m为正整数。由式(13)可得，其故障特征频谱不止一条，但只有当m=1时特征分量幅值最大，受基波影响相对较小，易于被检测，所以取f1-fr，f1+fr作为转子偏心故障低频段的左右边频故障特征分量。

2.1.1 小波包分析结合FFT提取故障特征

应用FFT的不足：FFT是一种全局变换，无法准确表达出信号的时频局域性质；FFT存在频谱泄露或噪声等,湮没故障特征频谱；对于存在非平稳信号，可能会有较高误判率。

小波包分析的优势：具有良好的时频局部性，通过伸缩和平移可进一步细化分析信号；其灵活的变换能够将故障诊断所需要的频率放大，进行多尺度分析，且对于处理微弱故障特征、非平稳信号和瞬时性的突变故障信号更为适用；用频段对频率进行分解，所以通过提高小波分辨率就可有效避免FFT存在的频谱泄漏等缺陷。

基于以上分析，本文提出将小波包分析结合FFT提取特征法应用于电机转子偏心故障诊断，并应用MATLAB验证该法的有效性。主要诊断过程是将采集获取的电流信号进行恰当有效分解层的小波包分解运算，再根据理论计算得出的故障特征频率分量，对特定频率段上的小波包先后实现波形重构，最后通过FFT分解得出诊断所需要的特定频段上的重构频谱图，通过分析频谱图最终实现偏心故障诊断。

(1) 小波包分解与重构

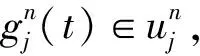
(14)

分解算法：

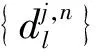
(15)

(16)

重构算法：

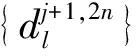
(17)

式中：h，g为滤波器系数；d为分解层数；j，n为小波包节点；l，k为分解层数。小波包分解是指将信号分成近似和细节两部分，且它们均可进一步细化分解，具体示意如图3所示。图3中，S为原始信号，A，D分别为近似，小波包分解树分解为3层，如果最高频率为f，则可将频率段0～f等分为8段。

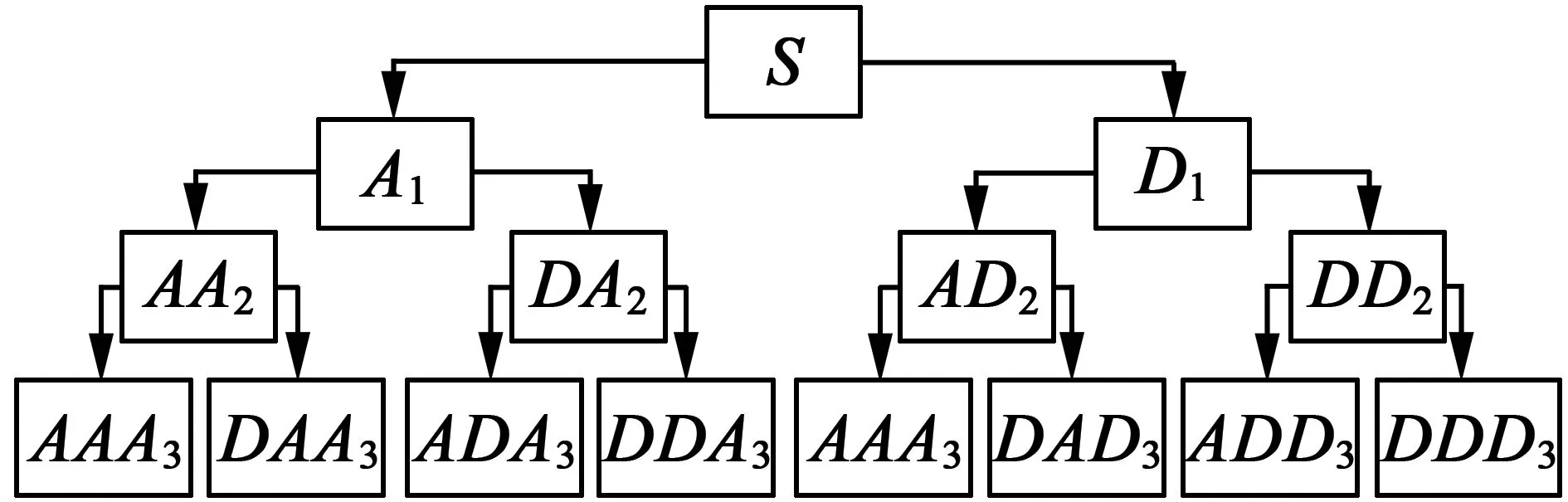
图3 小波包分解树示意图

正因为小波包在低、高频都具有良好的分辨率，所以在电机故障诊断具有明显优势。

(2) 改进方法在电机故障诊断领域的应用

小波包的应用大多通过把信号分解到不同层次频率带，应用小波包分解系数计算出能量特征值进行对比分析来判断故障，但这种做法无法得到表征故障的特征频率及其幅值大小。而对于诊断转子偏心故障是需要找到其故障特征频率的，傅里叶变换能实现对信号的频谱分析，所以将小波包分解后在特定段上进行波形重构，再对该重构波形进行频谱分析，即利用小波包分析结合FFT会是一种很好提取故障特征的方法。

2.1.2 应用MATLAB提取电流特征频率

本文利用从某石化公司实际电机中采集到的三相电流数据做频谱分析。由于条件限制，并未对电机进行一定程度上的偏心改装，其实在实际中，即便是新电机，由于一些加工或安装误差也会出现一定程度上的偏心。电流数据来自一台Z2=34的两极三相感应电动机，根据故障特征频率，式(11)、式(12)、式(13)进行计算时，nws取1可得出，高频段的故障特征频率：静偏心故障为883 Hz，783 Hz；动偏心故障为748.5 Hz，858.5 Hz，807.5 Hz，907.5 Hz。低频段的故障特征频率为25.5 Hz，74.5 Hz。

(1) 直接FFT提取特征频率

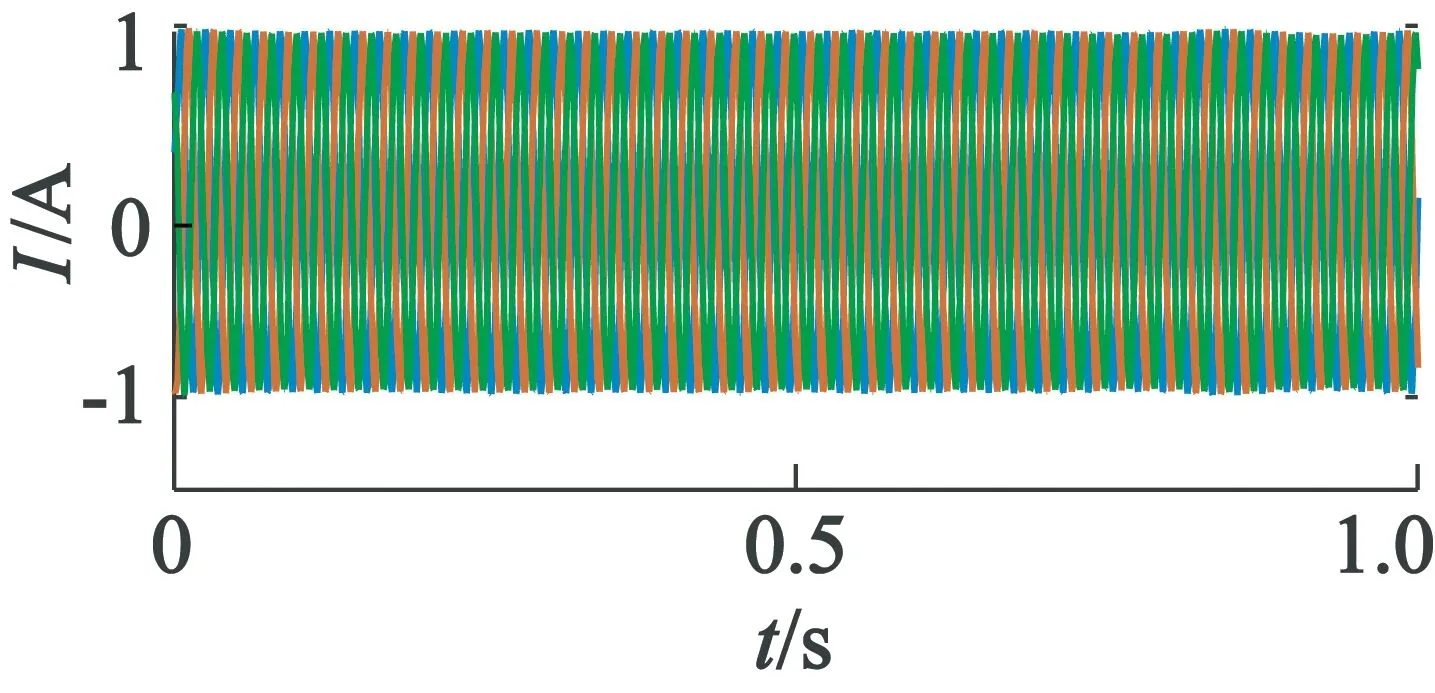
采集的三相定子电流原始波形如图4所示。在MATLAB中利用fft函数进行频谱分析，所得频谱图如图5所示，图5(a)和图5(b)分别为截取的低频段和高频段结果。

图4 定子三相电流波形

(b) 三相电流高频段频谱

图5(b)中在858.5 Hz，907.5 Hz附近产生了尖峰，与转子偏心故障时的故障特征分量相符合，说明应用FFT能够大致有效地提取出高频特征(因为高频特征频率与基频存在一定差距)，可得出此电机可能存在偏心。但由图5(a)并不能明显看出其低频故障特征频率，尤其对于故障早期，直接用FFT提取故障特征分量存在一定的局限性。

(2) 小波包分析结合FFT提取特征频率

由于采样频率为8 kHz，奈奎斯特频率4 kHz。根据前文理论计算出的特征频率，对电流信号进行5层小波包分解，划分成频率步长为125 Hz，小波基函数选为coif5，并对小波包分解的信号进行逐层重构，提取出各层节点的重构信号，最后联系理论故障特征所处的大致高低频段范围，对关键节点的重构信号进行FFT频谱分析。

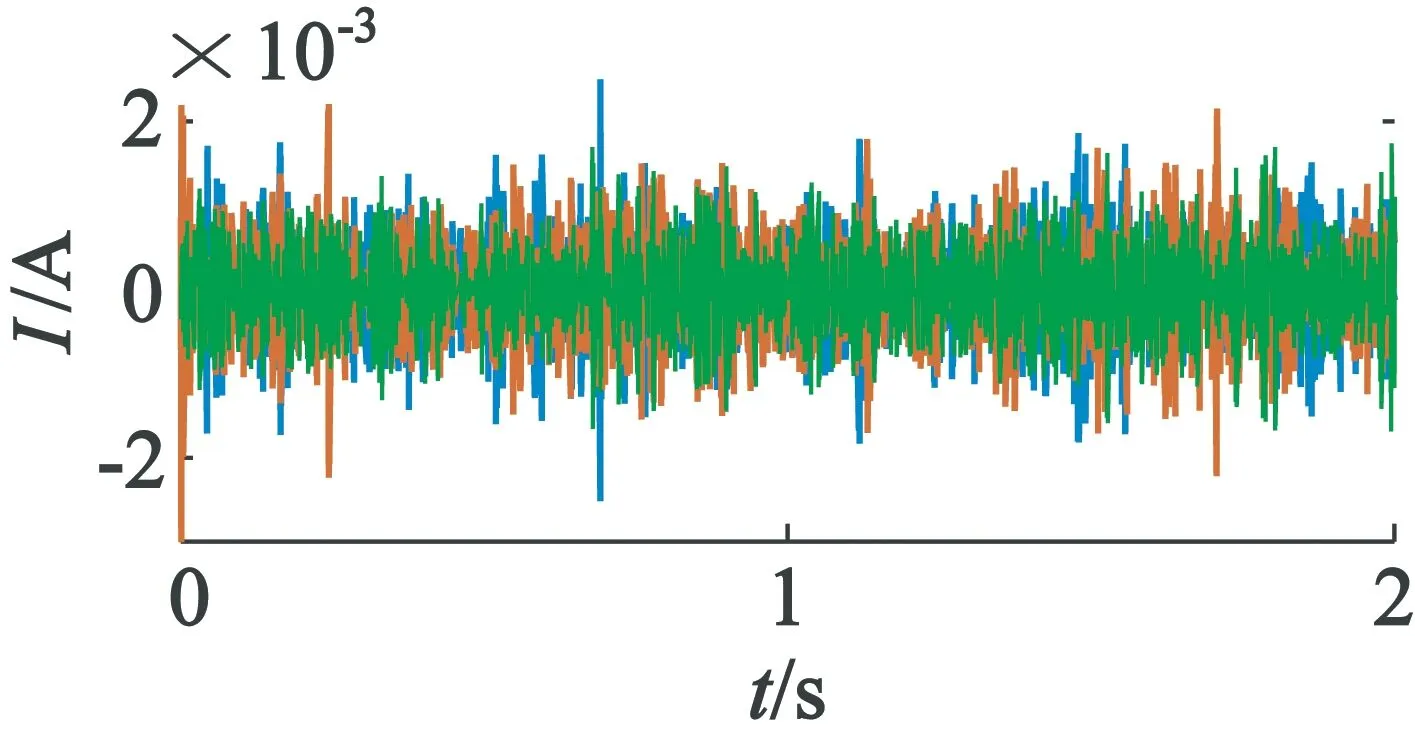
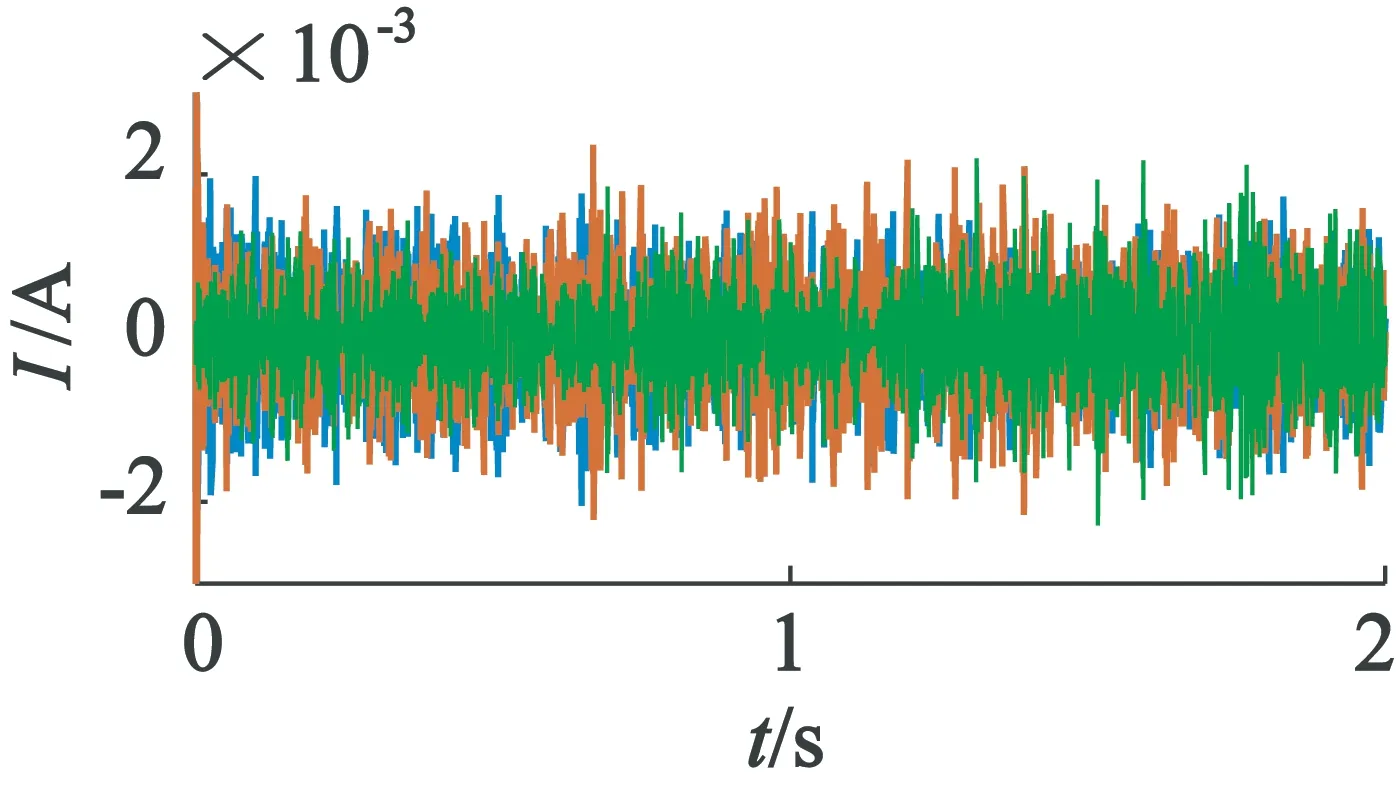
本文在MATLAB中实现上述过程，理论计算频段内关键节点的重构电流信号如图6所示。最后将(5,0)节点与(5,4)，(5,5)，(5,7)三个节点的重构信号进行FFT分析，得到相应频段频谱结果，如图7所示。本文遵循一定规律，调整取节点(5,4)，(5,5)，(5,7)的信号叠加再进行FFT，可避免小波包进行快速算法时出现频带交错现象。

(a) (5,0)节点

(b) (5,4)节点

(c) (5,5)节点

(d) (5,7)节点

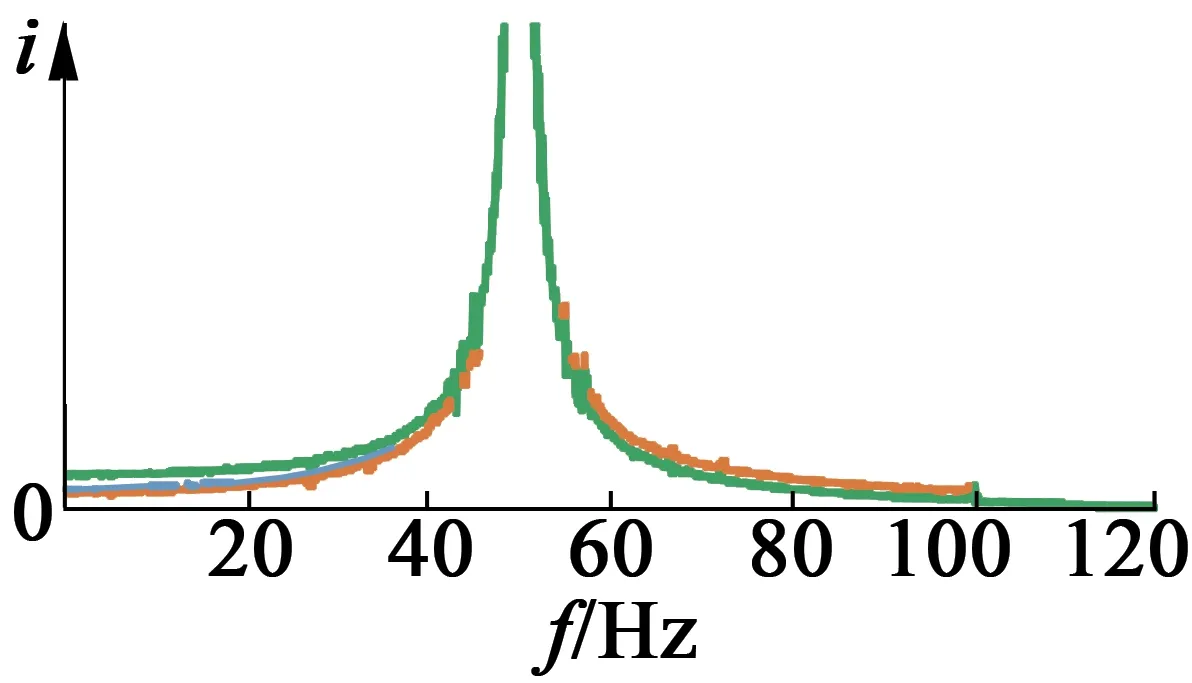
(a) 三相电流低频段频谱

(b) 三相电流高频段频谱

由图7可见，低频段25.5 Hz和74.5 Hz附近，高频段860 Hz和907 Hz附近，均出现能表征转子偏心故障的特征频率，但低频故障特征分量表现还是不够明显。实际上感应电动机的偏心在一定范围内是可忽略不计的，只有偏心程度较大时，其特征才会明显地表现出来。据以上频谱分析可知，一般电机都会存在一定程度上的混合偏心。

2.1.3 MATLAB处理结果分析

综上分析得出，对电机电流信号做频谱分析，看是否存在表征转子偏心的对应故障特征能够实现诊断要求。本文成功提取到故障特征，表明了理论计算的特征频率能作为转子偏心故障的有效判据，转子偏心后，定子电流中低频段会存在f1±mfr特征频率分量，中高频段会存在f1[(Z2±nd)(1-s)/p±1]特征频率成分。对于稳定信号,直接做FFT可有效地提取出故障特征分量，但在故障特征不明显、表现微弱，或存在频谱泄露等因素影响时会有局限性。而利用小波包结合FFT则可较准确有效地识别到偏心故障高、低频段的特征频率，并与理论分析一致，证实了改进方法的可行性。

2.2 不平衡磁拉力分析法

感应电动机运行在电磁场中，存在使转子旋转的切向力外，同时也会存在随时空变化的径向电磁力。转子偏心会产生不平衡拉力，这些力会使电机产生振动，严重影响其正常运行。本文依照电磁场理论得出电机偏心时的径向电磁力表达式，分析故障状态时电磁力特性和故障特征，并通过ANSYS仿真加以验证。

2.2.1 偏心时电磁力理论分析

实际运行中，电机动、静态偏心大都同时存在，且据本文对混合偏心状态相关物理量式(1)、式(4)、式(7)等推导，能够得出转子偏心时，在正常情况下所存在的气隙磁场之外，还额外附加了磁场次数为p±1，v±1，μ±1，其频率为ωs，ωs±ωr，ωr±ωr(ωs是电源角频率)的相关磁场，并且附加的磁场幅值与转子偏心程度成正相关。研究分析径向电磁力时，不仅要考虑基波磁场产生的幅值大、阶次低的力波(对电机影响正比于幅值，反比于阶次四次方)，而且还要考虑由定转子谐波磁场间相互作用情况下所产生的径向应力[13]，忽略幅值小、阶次高的力波，则径向电磁应力：

转子静偏心时，其附加磁场与基波磁场相互作用后,可能会产生2p±1、±1等低阶次力波，出现频率ωs±ωs(0频率也许会产生)，这些频率与无偏心理想情况时的频率状况一样；转子动偏心时，相应的可产生p±(p±1)、±1等低阶次力波，且产生了区别于正常和静偏心情况的其他特征频率：2ωs±ωr,±ωr,2(ωs±ωr)。具体特征情况如表2所示。

表2 感应电动机主要力波阶次及特征频率

分析表2可得出，感应电机径向电磁力的故障特征是：若存在奇次径向力波，即存在偏心故障；若电磁力频率出现2ωs±ωr，±ωr，2(ωs±ωr)，ωs，即存在动偏心。

2.2.2 ANSYS有限元建模仿真

本文在ANSYS中应用参数化语言，对气隙长度取1 mm，槽配合为36/28，定子内径、外径为210 mm，380 mm等相关参数的1极三相感应电动机，建立转子理想状态、静偏心和动偏心三种情况下的模型(偏心程度研究45%)，所建几何模型及网络剖分如图8所示。仿真分析三种状况下具体磁场分布状态，运用Maxwell应力张量法公式，计算获得相应电磁力分布情况，最后根据径向电磁力随空间和时间的变化，分别采用傅里叶分解得到对应的径向电磁力力波阶次图和相应的频域结果。

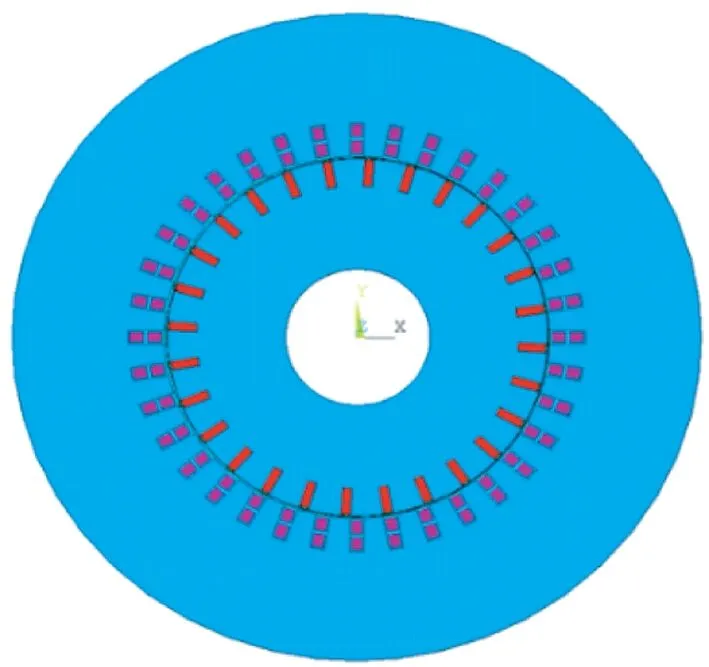
(a) 二维几何模型

(b) 气隙部分剖分

(c) 除气隙外剖分

对电机模型进行网格剖分控制，求解控制设置电磁力边界条件，根据一般感应电动机的实际运行状态，对仿真电机的定子绕组上施加电流密度作为激励，便可得到磁场分布。不同状态磁力线分布情况如图9所示。

对比图9(a)和图9(b)可得，偏心会使气隙距离一边大一边小，磁力线有偏移，且动偏心时气隙最小距离一直与旋转磁场一致，磁力线偏向气隙距离小的一侧。仿真得出电机三种情况下的气隙磁密分布如图10所示。

(a) 无偏心状态

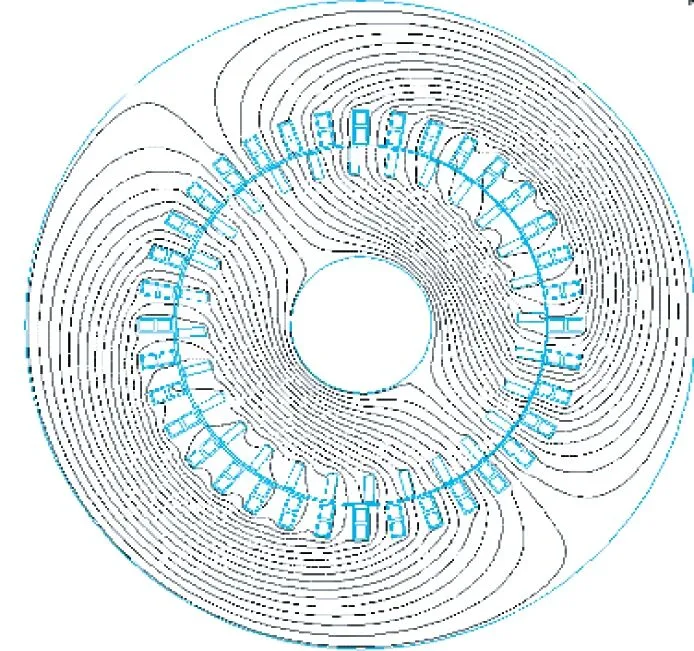
(b) 偏心状态

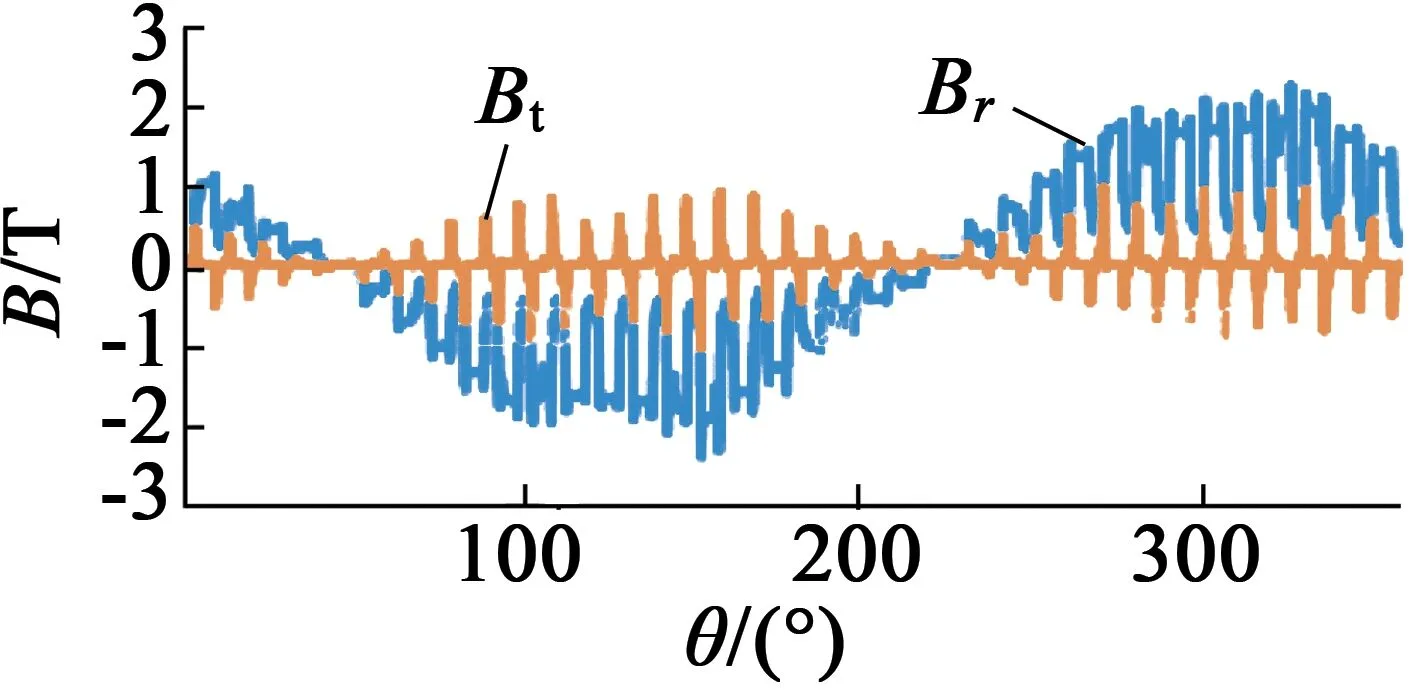
(a) 无偏心

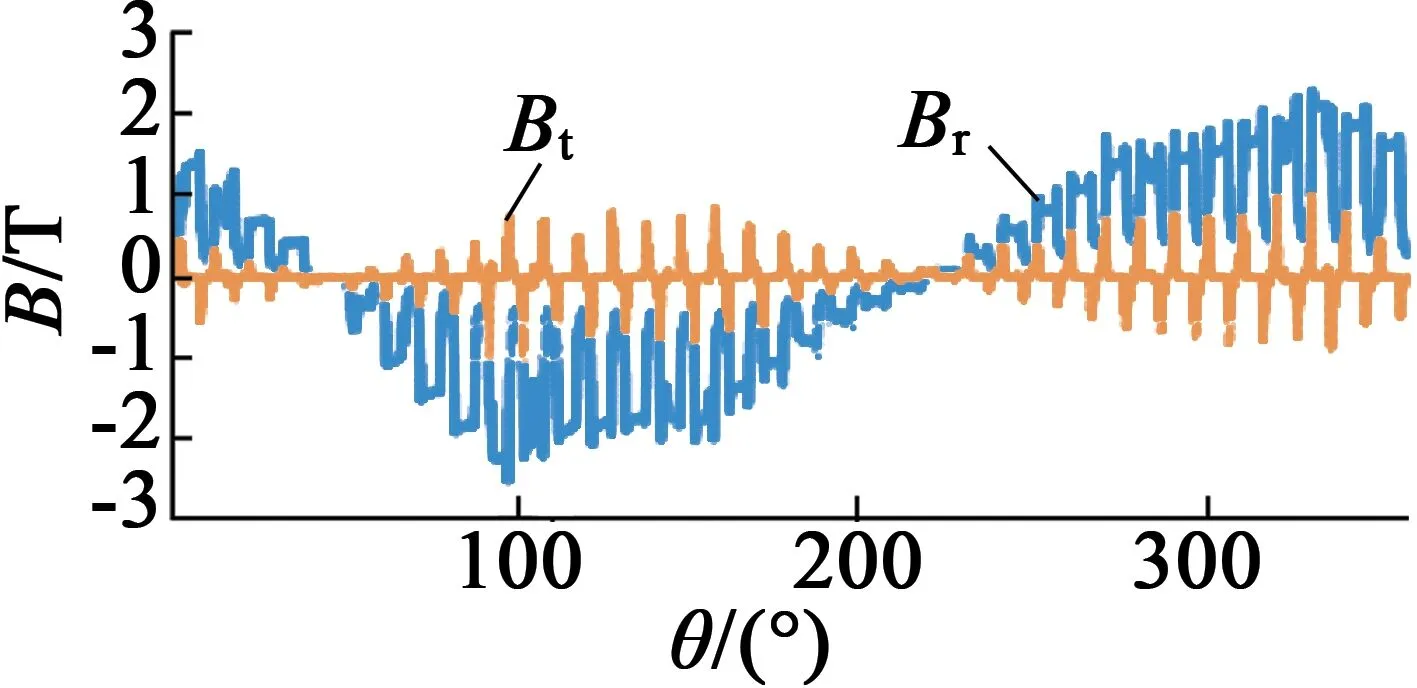
(c) 动偏心

由图10可得，磁密径向分量对气隙磁场的影响显然大于切向分量。由于存在相反磁场，使该磁场中间磁密为0，远离中间的磁密逐渐增大。且在定子齿表面上磁密近似是平的，但由于定、转子铁心上存在很多槽，使槽附近相对气隙距离增加，磁密急剧减小，使其局部存在锯齿变化。电机偏心导致气隙距离改变，而气隙磁密会随着距离的增加而减小，所以在气隙较小位置的磁密幅值要显著大于气隙较大位置的磁密。利用Maxwell应力张量法公式，得到电机三种状态下的径向电磁力随着空间变化结果，如图11所示。

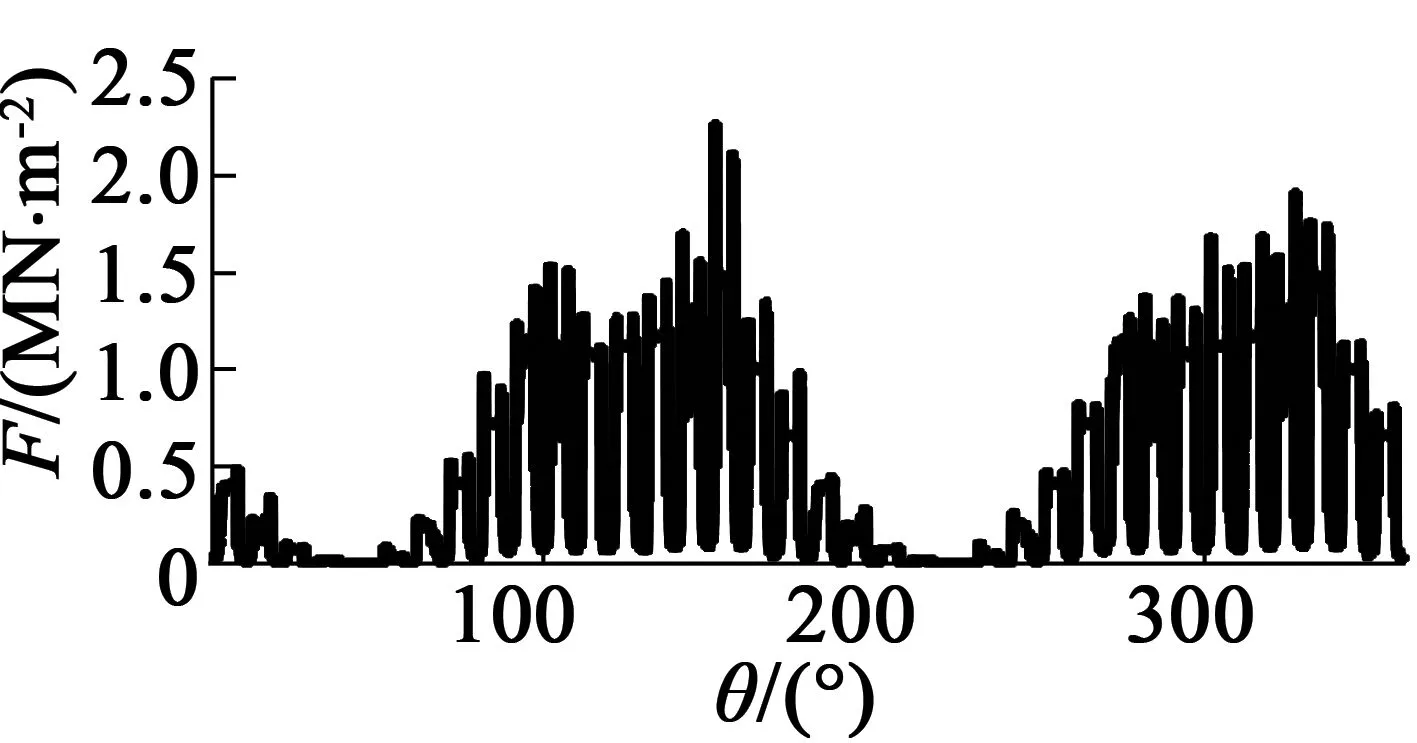
(a) 无偏心

(b) 静偏心

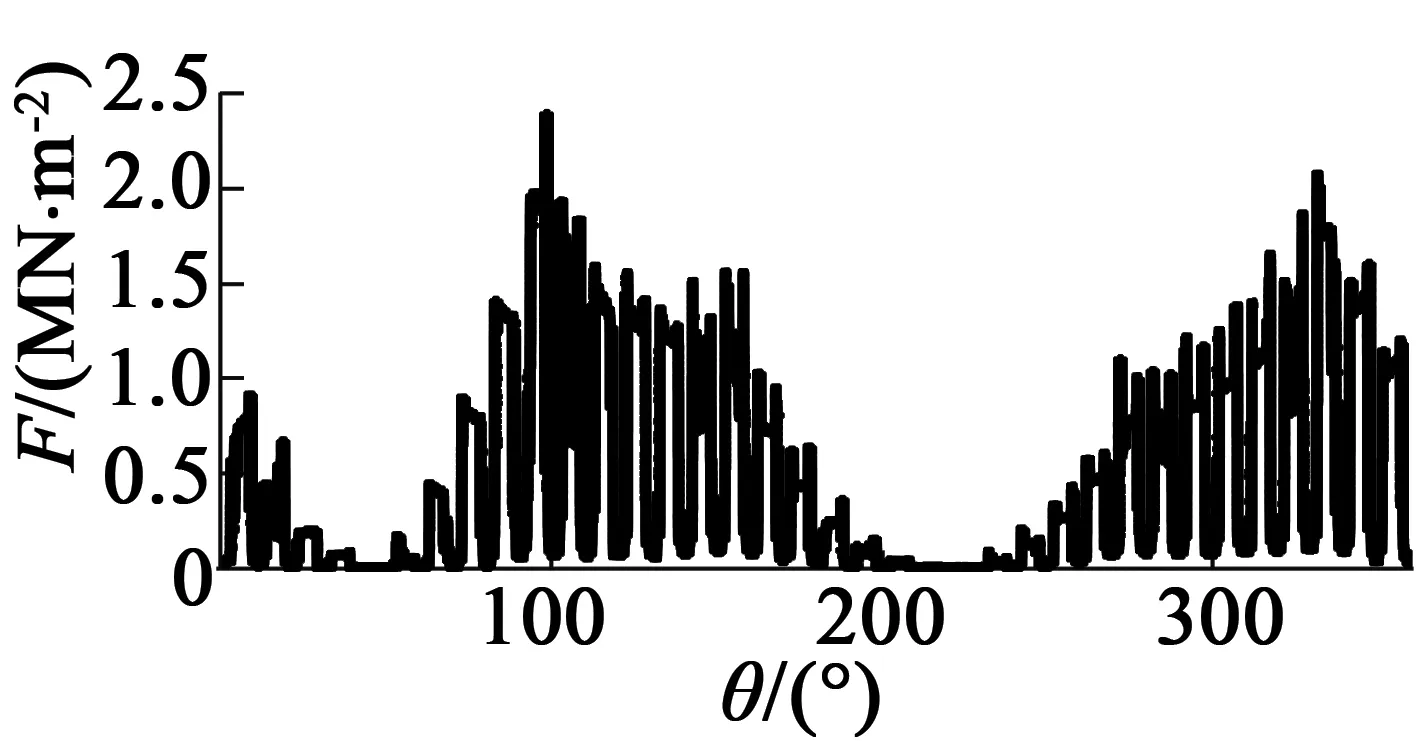
(c) 动偏心

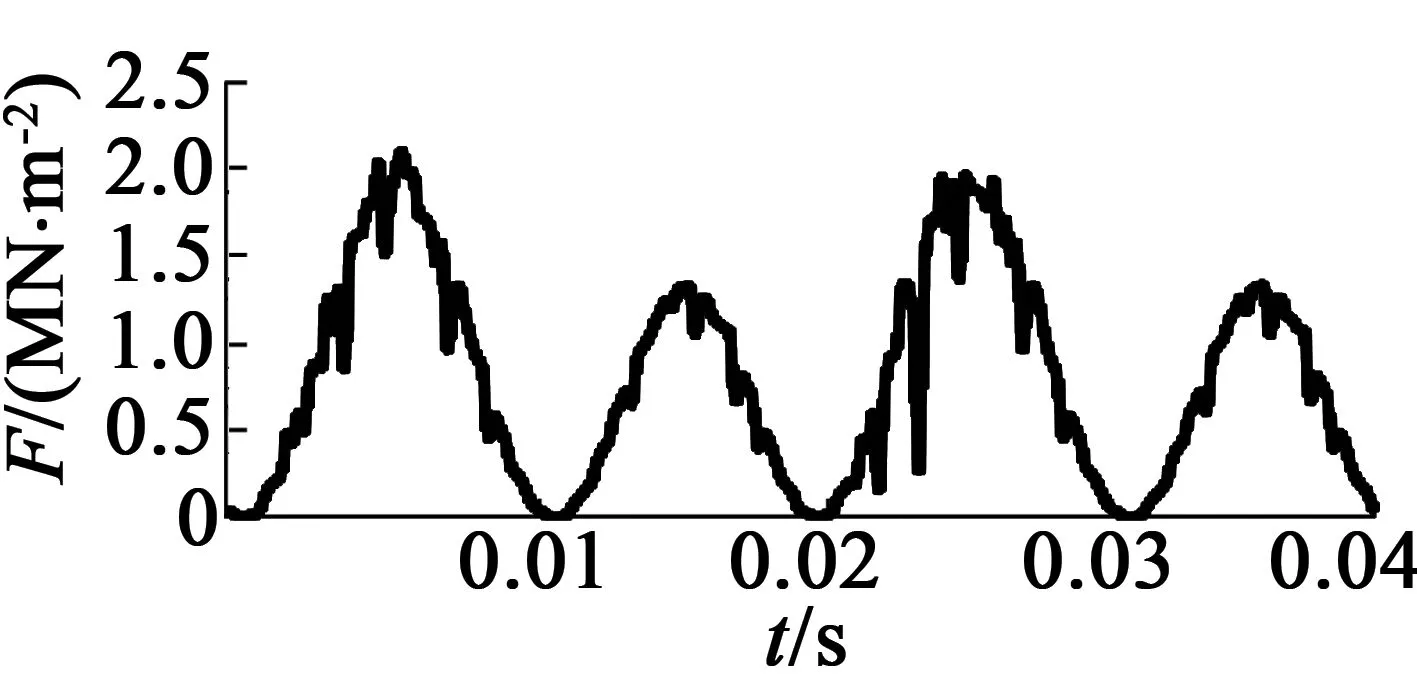
无偏心时径向力随空间分布存在局部急剧起伏，经分析依然是受定、转子铁心上槽的影响。偏心故障时，气隙磁密变化还有磁场间相互作用使电磁力也随之改变，使其分布不对称。选取电机90°位置气隙中间节点，得到径向电磁力随着时间变化结果，如图12所示。

(a) 无偏心

(b) 静偏心

(c) 动偏心

无偏心状态下，径向力随时间分布大体呈正弦变化，曲线异常波动是源于电机旋转时气隙磁导的改变，且径向力主要成分是2倍电源频率；静偏心电磁力在某一点上的变化转换到相应频率上是不会受到影响的，只是其幅值会有所变化；动偏心电磁力峰值呈由大到小再由小到大的变化，分析原因是90°位置气隙距离在转子旋转过程中呈由小到大的周期变化。对图11三种情况径向力随空间变化进行傅里叶分解，得到力波阶次如图13所示。

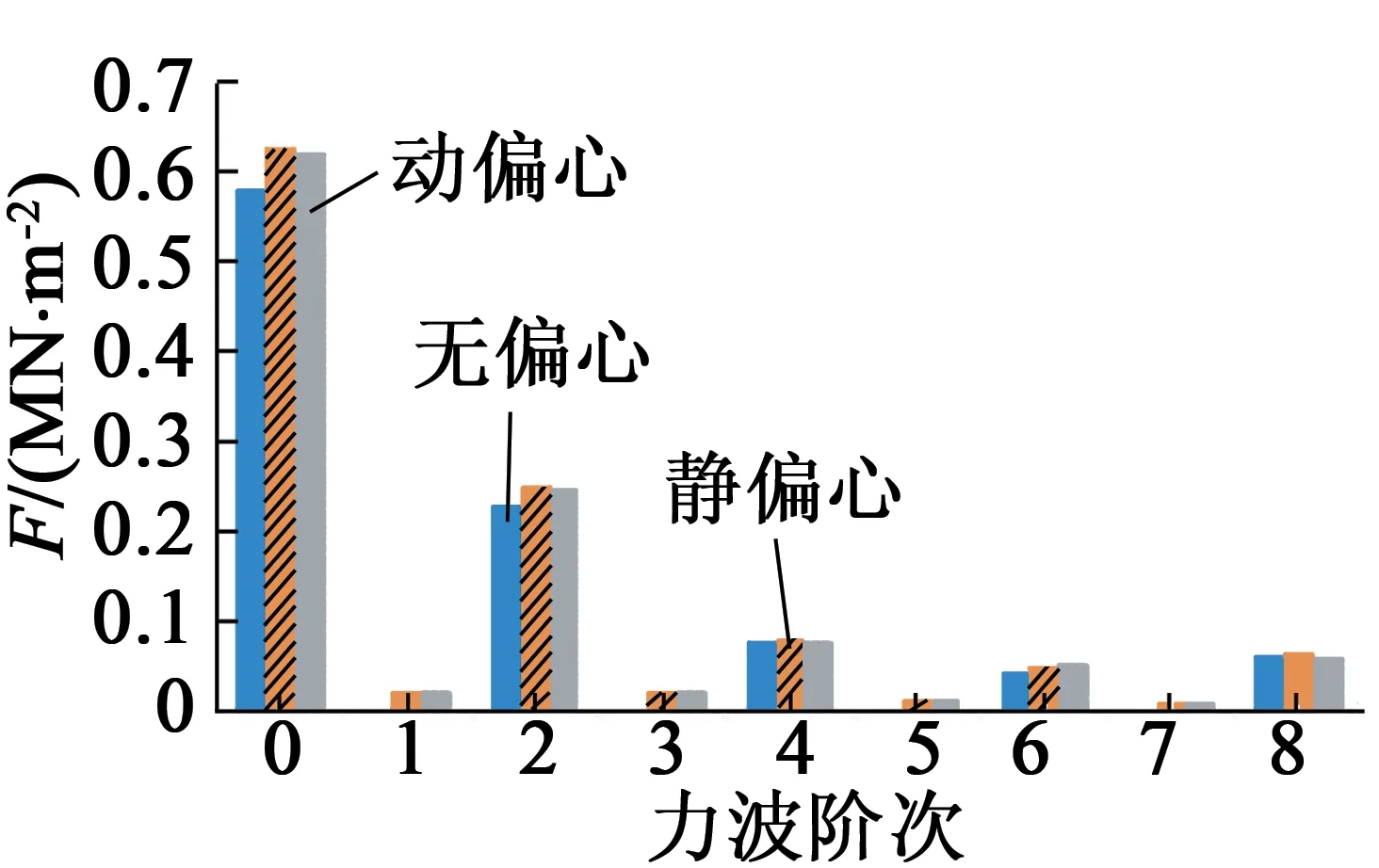
图13 径向电磁力力波阶次图

由图13可得，感应电动机转子在理想情况时会产生0,2,4等偶数次力波，存在偏心后力波次数比正常状态时增加了1,3,5等低阶奇数次，仿真结果与之前理论得出偏心时会产生奇次力波结论相吻合，证实了其故障特征的准确性。对图12三种情况径向力随时间变化进行傅里叶分解，得到径向力频域结果如图14所示。

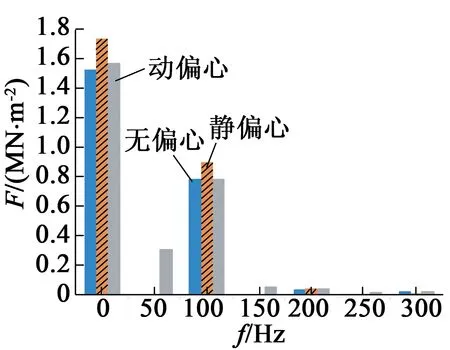
(a) 径向力0～300 Hz频域结果

(b) 径向力1 300～1 800 Hz频域结果

由图14可得，感应电动机无偏心状态出现的频率除100 Hz之外，还存在定转子齿谐波频率：1 300 Hz,1 400 Hz,1 500 Hz等。静偏心状态时出现的频率有：0,100 Hz,200 Hz,1 300 Hz,1 400 Hz等，与无偏心情况时的相同，但幅值不同。动偏心状态时出现的频率为0,50 Hz,100 Hz,150 Hz,200 Hz,250 Hz,1 300 Hz,1 350 Hz,1 400 Hz等，尤其在低频段上的频域特征表现更为明显。

2.2.3 仿真结果分析

感应电动机偏心故障时，径向电磁力特征除正常情况下存在偶次力波外同时还会存在±1，2p±1奇数次力波及计及齿槽效应存在的v±μ±1次力波；动偏心时径向力频率出现区别于正常与静偏心状态±ωr,2ωs±ωr,2(ωs±ωr) 新的特征频率，ANSYS仿真结果同理论相吻合，验证了这些故障特征的有效性。

2.3 振动信号分析法

实际上，感应电动机转子偏心故障引起的异常振动很大程度上源于径向电磁力，而且故障时产生的新的低阶次力波影响较大。若出现存在的力波阶次及频率同电机某阶模态所对应状态相同，便会产生谐振，使振动与噪声明显增加，因此振动信号法就可利用这种异常振动信号，间接反映磁场的变化，客观地反映电机的运行状态。

结合上文对径向电磁力研究的相关结论及基于振动信号频谱分析的诊断法，对于实际应用中较易发生的混合偏心故障进行综合分析可得出，故障特征频率有fr，2fs，2fs+fr等，还有引入的0在诊断中的参考与应用[14]。具体特征频率静偏心为2fs，0；动偏心为fr，2fs±fr(实际常用特征频率fr)。特征频率幅值能够反映对应故障的严重程度，其中反映静偏心的0和反映动偏心的fr，其幅值大小基本与对应故障的严重程度成正线性相关，且fr下的动偏心的电磁振动以1/(2sfs)周期进行脉动。

振动信号分析法优点是节约成本，降低并简化信号处理的难度；但个别特征频率没有很好的灵敏性，不适用小程度偏心状态的故障诊断。

3 结 语

小波包分析兼顾时频局部化分析且具有良好分辨率，能对信号进行多尺度分解、细化频率，将电流信号小波包分解后再对故障频段重构信号进行FFT频谱分析，能够有效提取低频与高频电流故障特征，提高电机故障诊断判别率。

根据ANSYS径向电磁力仿真结果，可得出转子偏心时径向力会存在±1，2p±1奇数次力波及计及齿槽效应存在的v±μ±1次力波；静偏心时会出现0等频率；动偏心时会出现±ωr,2ωs±ωr,2(ωs±ωr) 等新特征频率，尤其是ωr。该结论也为振动信号法提出的特征频率提供理论依据，对电机故障诊断研究发挥积极作用。

对比分析了三种诊断方法，定子电流频谱法最优，振动信号分析法次之，不平衡磁拉力法最差。定子电流信号较其他参数受外界干扰最小，便于检测和分析；同时定子电流与振动信号法能够做到尽量小的电机侵入甚至无侵入，实用性较好。