负载波动下感应电动机转子断条故障诊断

吴文军，张晋瑞，尚 仪

(1.国网四川省电力公司天府新区供电公司，成都 610041； 2.东北师范大学，长春 130024)

0 引 言

感应电动机是工农业生产中重要的旋转设备，但是其发生转子断条或端环开裂的概率却仍然高达10%左右。对感应电动机转子故障进行及时有效的检测显得尤为重要[1]。目前，恒定负载感应电动机转子断条故障检测方法已取得良好的成果，并在工业实际中有了成功的应用。

基于定子电流特性分析(以下简称MCSA)是较为常用的感应电动机转子断条故障检测方法[2]。当感应电动机定子电流频谱中出现大小为(1±2s)f1的频率分量(f1为供电频率，即定子电流基频分量，s为转差率)时，电机则发生转子断条故障，因此在判断转子断条故障时可以以该边频分量作为特征频率[3]。如快速傅里叶变换(以下简称FFT)及其变形(如Zoom FFT)[4]是最为常用的电流特性分析方法[5]。

为了克服FFT存在的频谱泄露、频率分辨不够等固有局限，基于谱估计的转子断条故障检测方法也被成功引入。目前已经成功应用于感应电动机转子断条故障检测且取得良好效果的新兴频谱分析算法包括：多重信号分类算法(以下简称MUSIC)[6-8]、旋转不变参数估计技术(以下简称ESPRIT)[9-10]、Prony方法[11]等。MUSIC作为现代谱估计技术，相比于FFT，即使对于短时数据情况，MUSIC仍然能够保持较高的频率分辨率，而对于信号的幅值和相位参数，MUSIC通常借助模拟退火算法[12]、遗传算法[13]和模式搜索算法[14]等智能优化算法进行估计。同理，ESPRIT同样具有较好的频率分辨率，可是对于幅值和相位参数估计精度较差，故通常也将该方法与智能优化算法相结合[15]。Prony方法可以同时检测信号的频率、幅值和相位角，是一种理想的故障检测方法。

为了更好地凸显故障特征，定子电流变换方法也被成功用于转子断条故障检测之中。如Park变换及Park矢量模平方函数[16]、Hilbert模量等电流变换形式[17]；不仅如此，瞬时有功(无功)功率也得到了应用[18]。这类方法不同于传统的基于MCSA方法，它们均是通过对定子电流的变形、坐标变换或者同时利用电压电流信号进行特征故障检测的。这类方法有一个共同的特点：可以有效地使故障特征频率(1±2s)f1远离基频分量f1，从而避免被淹没或者频谱泄露。不仅如此，当定子电压电流信号经过这些方法处理之后往往可以将基频分量转化为直流成分，再经过一定的处理便可以滤除直流成分，凸显故障特征，提高故障检测能力。

由以上分析可知，对于恒定负载下的感应电动机转子断条故障检测方法已有较为成熟的研究。但是，以上方法并未考虑负载波动的情况。当电机拖动负载表现为一个恒定负载转矩和一个单一确定频率成分的波动负载转矩叠加而成时，此种情况称为负载波动。当负载波动的频率为fL时，会在定子电流频谱中叠加一个大小为(f1±fL)的频率成分，当其与断条故障特征频率(1±2s)f1接近时，负载波动可能会对转子断条故障检测引起误判。为了提高感应电动机转子断条故障检测可靠性，须将其与负载波动进行有效区分。

研究表明，转子断条故障和负载波动在瞬时有功(无功)功率的表现是不同的[19]：转子断条故障和负载波动均会在瞬时有功功率(以下简称IAP)调制出大小分别为2sf1，fL的频率成分，但是幅值则表现为后者远大于前者；同理，在瞬时无功功率(以下简称IRP)同样存在大小分别为2sf1，fL的频率成分，但是幅值为前者远大于后者[20-21]。据此，便可以对转子断条故障与负载波动进行有效的区分。文献[19]的方法虽然可以对转子断条故障与负载波动进行区分，但是当二者同时存在且2sf1，fL极其接近甚至相同时，现有的频谱分析技术是无法将二者进行区分的；文献[21]在回顾与拓展了转子断条故障与负载波动识别方法的理论基础，给出了明确的诊断判据，但是该方法亦是建立在频谱分析的基础上(这对频谱分析技术要求较高)，且未考虑2sf1，fL相同的情况。

不仅如此，以上方法只是涉及到如何对负载波动与断条故障进行有效检测与区分，并未考虑提取故障特征之后的状态识别问题。目前常用的分类算法有人工神经网络(以下简称ANN)[22]、支持向量机(以下简称SVM)[23]和随机森林(以下简称RF)[24]等。ANN和SVM均为单一分类器，其分类正确率还有待进一步提高。而RF属于集成分类器，其具有分类速度快、正确率高的特点。

基于此，本文针对负载波动下感应电动机转子断条故障特征提取和状态识别问题，提出了基于瞬时功率与离散小波相结合的故障特征提取方法，并给出了明确的小波判据；然后构建了以RF为基分类器的集成分类器，从而实现对负载波动下感应电动机转子断条故障的准确有效诊断。

1 负载波动下断条故障特征及问题分析

1.1 恒定负载下断条故障特征分析

当感应电动机出现断条故障时将在定子电流中产生一个频率为(1-2s)f1的边频分量。该边频分量将导致定子电流幅值出现周期性变化，进而反作用到转子上，产生一个两倍转差率的力矩。又因为转子的转动惯量不可能无限大，故该两倍转差率的力矩就会对转子的速度产生扰动。速度的扰动一方面会降低(1-2s)f1的下边频分量摆动幅度；另一方面会产生一个(1+2s)f1的上边频分量。

图1为恒定负载下感应电动机定子电流及其FFT频谱图。由图1可知，恒定负载先感应电动机发生转子断条故障时将在定子电流频谱中叠加两个频率大小为(1±2s)f1的边频分量，以此作为断条故障特征。

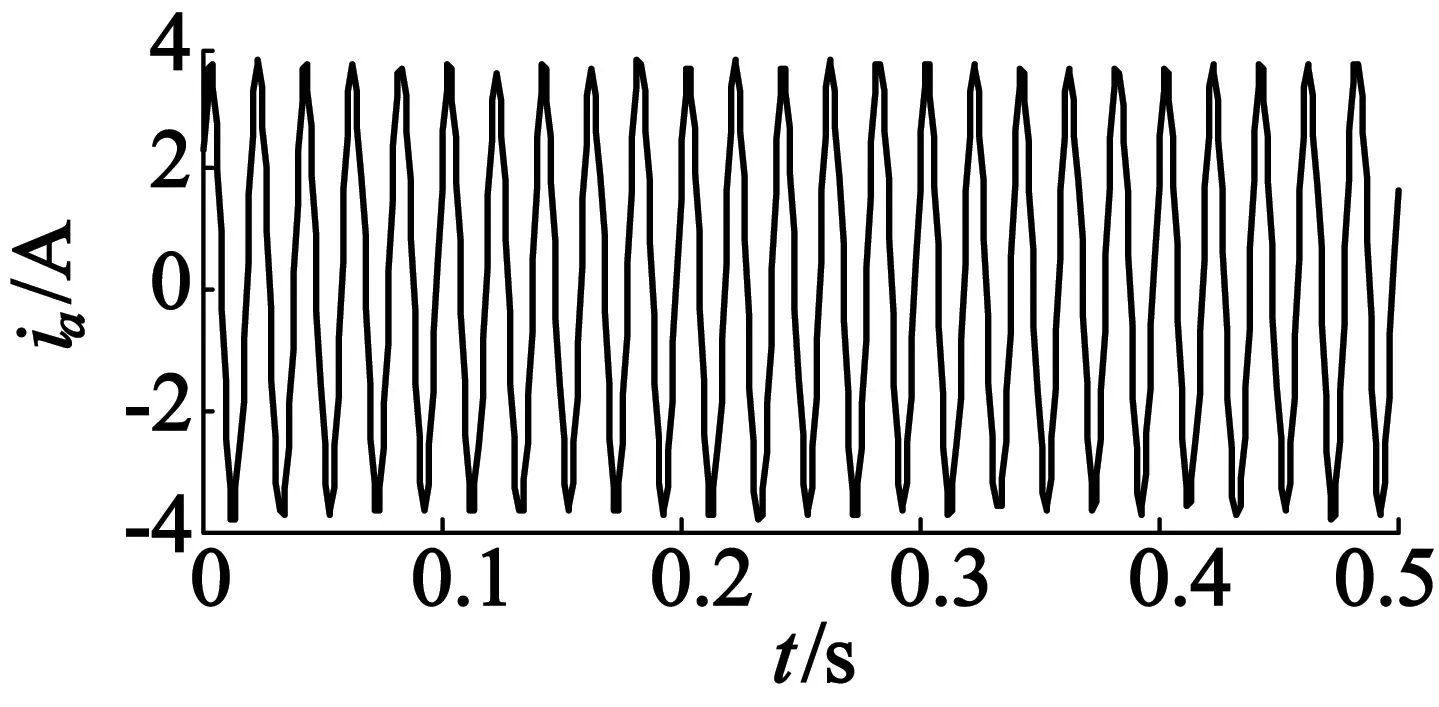
(a) 定子电流

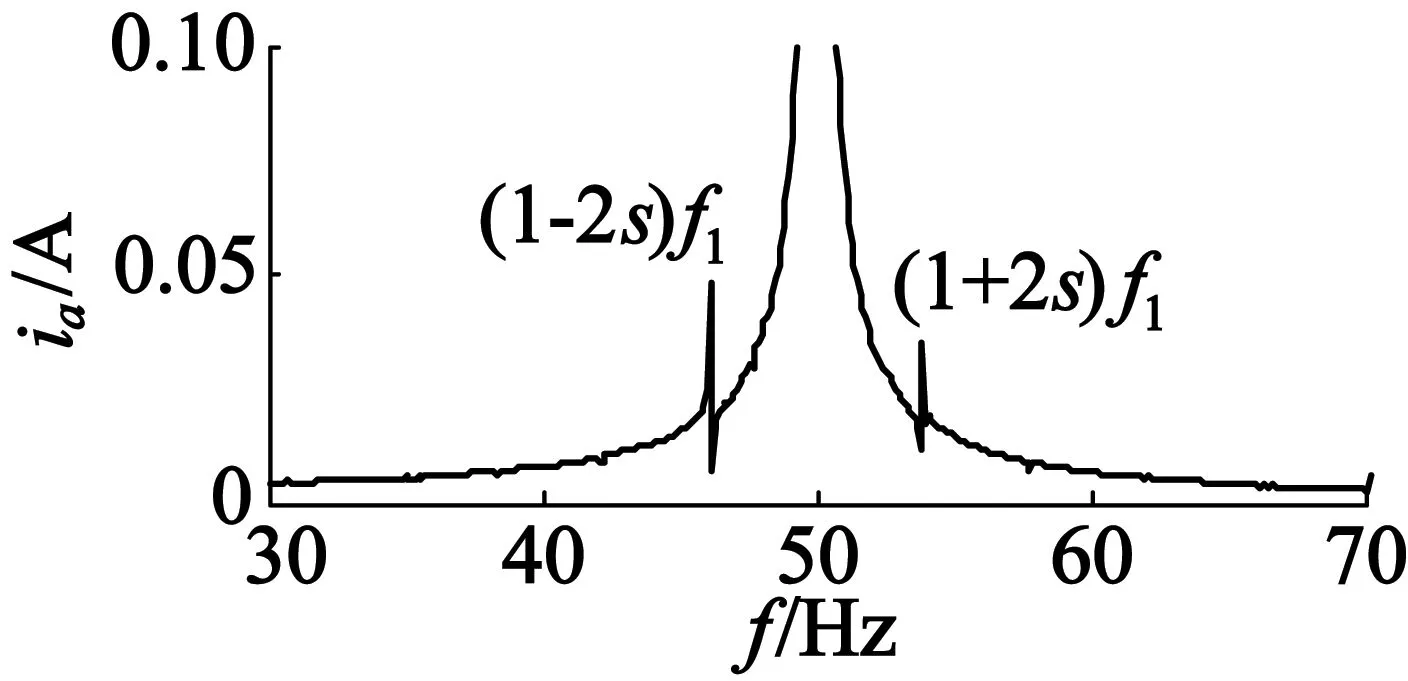
(b) 定子电流频谱

1.2 波动负载下断条故障特征分析

此处的波动负载为一个恒定负载转矩和一个单一确定频率成分的波动负载转矩叠加而成，表达式如下：

Tload=Tavg+ηTavgcos(2πfL)

式中：Tavg为恒定负载转矩；η为反映负载波动水平的系数；fL为波动频率。

当电动机负载转矩以频率fL进行波动时，电机的转速ωr和电磁转矩Te都将以同样的频率fL进行波动。同转子断条故障一样，由负载波动引起的转速波动也将影响定子绕组中的感应电动势，从而会在定子电流上叠加两个频率为f1±fL的电流成分，故当fL与2sf1极其接近时，负载的波动容易干扰转子断条故障特征频率的检测。

图2为负载波动下感应电动机定子电流及其FFT频谱图。由图2可知，当电动机出现转子断条故障时，定子电流频谱中会存在故障特征分量(1±2s)f1。但是当电机的负载呈现波动性质时会对定子电流进行一定的调制，从而导致在定子电流频谱分析时也出现边频分量f1±fL，从而混淆断条故障。

通过对负载波动下感应电动机转子断条故障特征分析，我们可以发现，当负载呈现波动性质时，波动特征频率会混淆断条故障特征，需将二者进行有效区分。

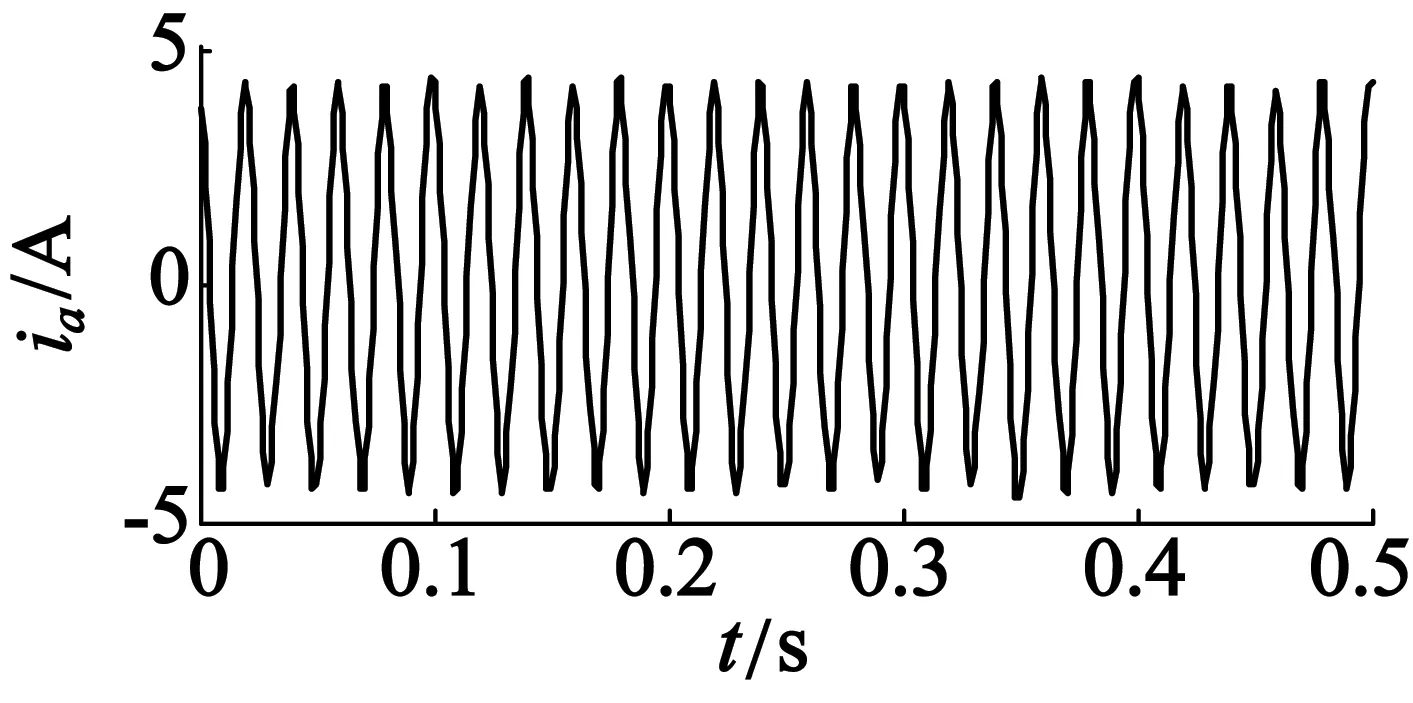
(a) 定子电流

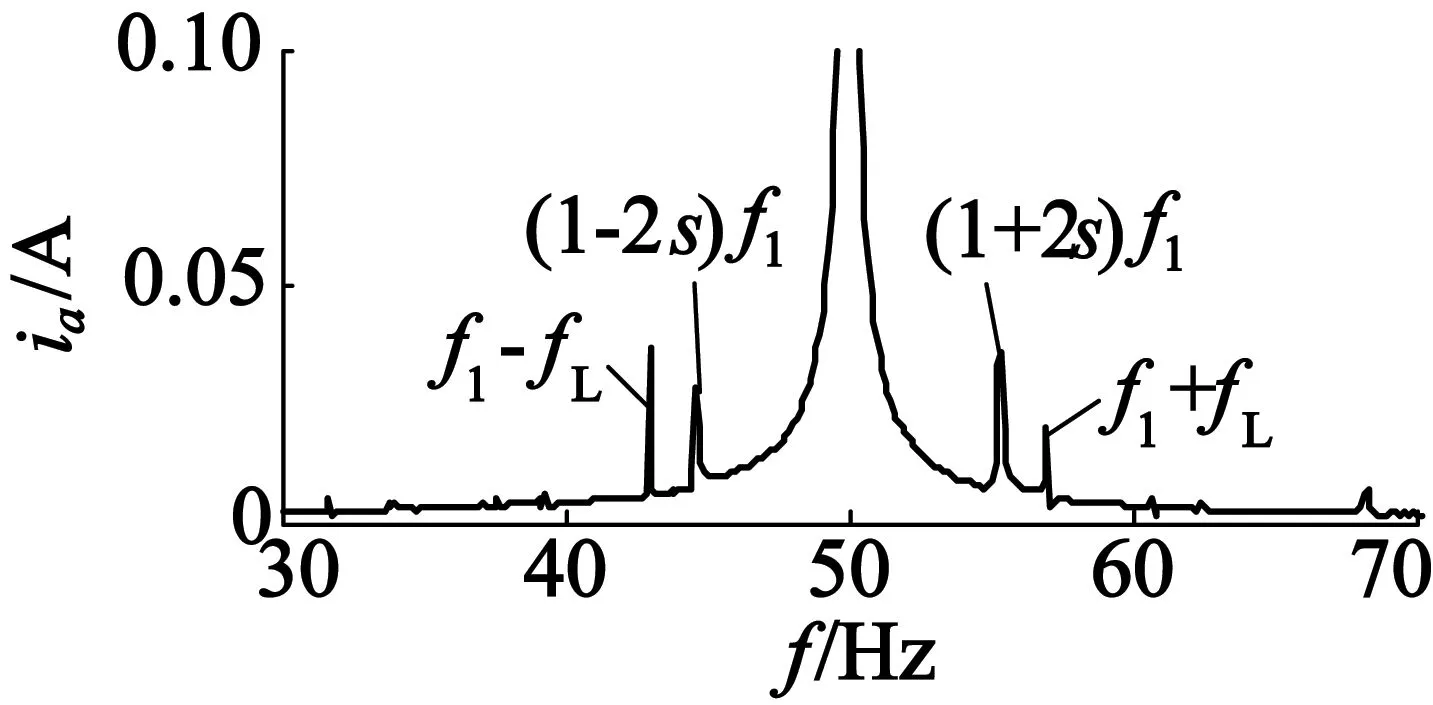
(b) 定子电流频谱

2 基于瞬时功率与离散小波的故障特征提取及新判据

2.1 恒定负载下断条故障电机瞬时功率

感应电动机定子电压经过Hilbert转化为复空间矢量后有如下表达式：

(1)

同理，对于感应电动机断条故障时定子一相电流的复空间矢量表达式如下：

(2)

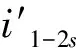
那么，感应电动机的瞬时有功、无功功率表达式[21]：

(3)

经过进一步推导，瞬时有功、无功功率可表示如下：

p(t)=3VIcosφ-3V[I1-2s-I2sbsinαs]·

sin[2π(2sf1)t+αT]≈3VIcosφ

(4)

cos[2π(2sf1)t+αT+ξ]

(5)

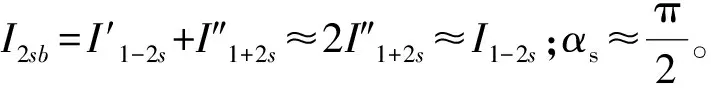
由式(4)、式(5)可知，恒定负载下，感应电动机出现转子断条故障时，故障特征频率成分2sf1主要在IRP中体现，其幅值远大于2sf1在IAP中的幅值。

2.2 波动负载下断条故障电机瞬时功率

当感应电动机同时存在转子断条故障与负载波动时，定子电压仍然如式(1)，而电流的复空间矢量如下：

(6)

那么，感应电动机的瞬时有功、无功功率表达式如下：

p(t)=3VIcosφ-3V(I1-2s-I2sbsinαs)·

sin[2π(2sf1)t+αT]+3VIlobsinαs·

sin(2πfLt+αT+δ)≈3VIcosφ-

3V(I1-2s-I2sb)sin[2π(2sf1)t+αT]+

3VIlobsin(2πfLt+αT+δ)≈3VIcosφ+

3VIlobsin(2πfLt+αT+δ)

(7)

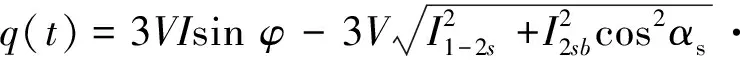
cos[2π(2sf1)t+αT+ξ]-3VIlob·

cosαssin (2πfLt+αT+δ)≈

3VIsinφ+3VI1-2s·

cos[2π(2sf1)t+αT+ξ]

(8)

由式(7)、式(8)可知，IAP中主要含有负载波动频率成分fL，其幅值大小主要由负载波动决定；IRP中主要含有断条故障特征频率成分2sf1，其幅值大小主要取决于转子断条故障。

因此，针对负载波动下感应电动机转子断条故障检测问题，只需要通过对IAP和IRP进行频谱分析,便可以将二者进行区分。

通过以上分析可知，通过瞬时功率可以排除负载波动对转子断条故障检测的影响，但是当2sf1，fL极其接近甚至相等时，传统的频谱分析技术是无法实现准确的故障检测的。为此，进一步引入离散小波变样(以下简称DWT)方法，对负载波动下电机瞬时功率进行频段分解并提取能量，以解决以上问题。

2.3 基于DWT的故障特征提取及小波判据

DWT作为一种时频分析工具，对非平稳信号具有良好的处理能力，故可用于负载波动下感应电动机转子断条故障时瞬时功率信号的处理。对于瞬时功率信号S，DWT将其分解为一个逼近信号al和一系列细节信号dj，其频段如下式：

(9)

式中：fs为信号采样频率；l为小波分解层数,取决于采样频率以及实际所需的频段宽度;j=1,2,…，l。

对逼近信号与细节信号提取能量，如下式：

(10)

式中：Nl为第l层的数据长度。

由于转子断条故障、负载波动会在IAP以及IRP中表现不同，对瞬时功率进行小波分解并提取频段能量，那么特征频率2sf1,fL所在频段的能量值将较比其他频段能量大。用Ep和Eq分别表示特征频率2sf1,fL所在频段的IAP和IRP小波能量幅值。负载波动下感应电动机转子断条故障诊断小波判据如表1所示。

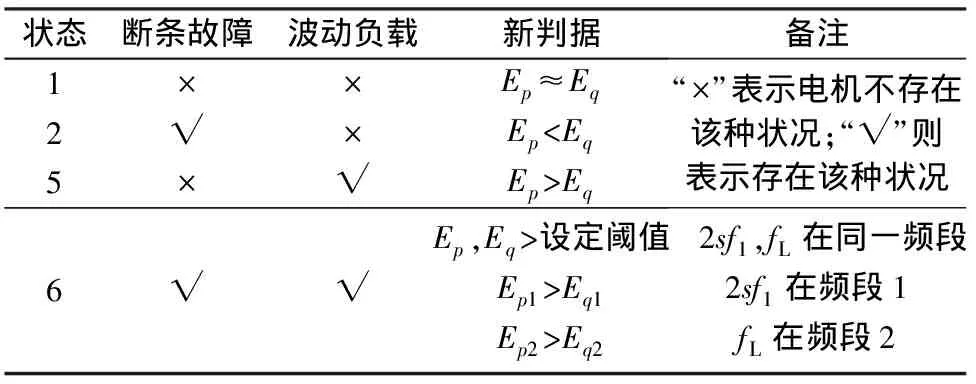
表1 变化负载下转子断条故障诊断小波判据

由表1可知，对于既存在断条故障，又存在负载波动的情况，如果二者的特征频率均分布在同一频段，那么将出现Ep和Eq均偏大，且大于设定阈值的情况；如果2sf1，fL分布在不同频段，那么2sf1所在频段EpEq。以上便是负载波动下感应电动机转子断条故障诊断小波判据，对于2sf1，fL非常接近甚至相等的情况，本方法仍然有效。

因此，通过结合瞬时功率与离散小波可有效提取负载波动下感应电动机出现转子断条故障特征。

3 集成分类器

3.1 集成学习原理

集成学习(以下简称EL)是一种使用多个分类器来解决同一个问题并以此提高泛化能力的机器学习方法。图3为集成学习原理。

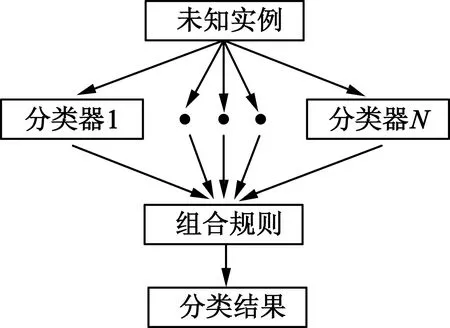
图3 集成学习原理

图3通过某种集成规则，将多个分类器集成起来，然后对一个未知实例进行分类或者预测，从而取得比单个分类器更加优良准确的性能，其中的单一分类器叫做元分类器或者基分类器。集成学习好比是一个拥有多个决策者的组织机构，然后让这个组织中的每个成员对同一件事物进行集体决策。

3.2 基于RF的集成分类器

RF本身就是一种集成分类器，其所有的基分类器都是决策树。RF是利用Bootstrap自助重采样，通过有放回且无权重方式对原始数据进行采样，然后将采样得到的不同数据,创建对应的不同决策树，再利用各个决策树对测试数据样本进行“投票表决”，最后将投票结果进行组合，由此便得到最终的分类结果。

RF分类算法之所以能够避免BP神经网络、SVM等分类算法的过拟合以及局部最优等问题，是由于其采用了集成学习思想，同时也真实体现了“随机性”。RF的流程如图4所示。

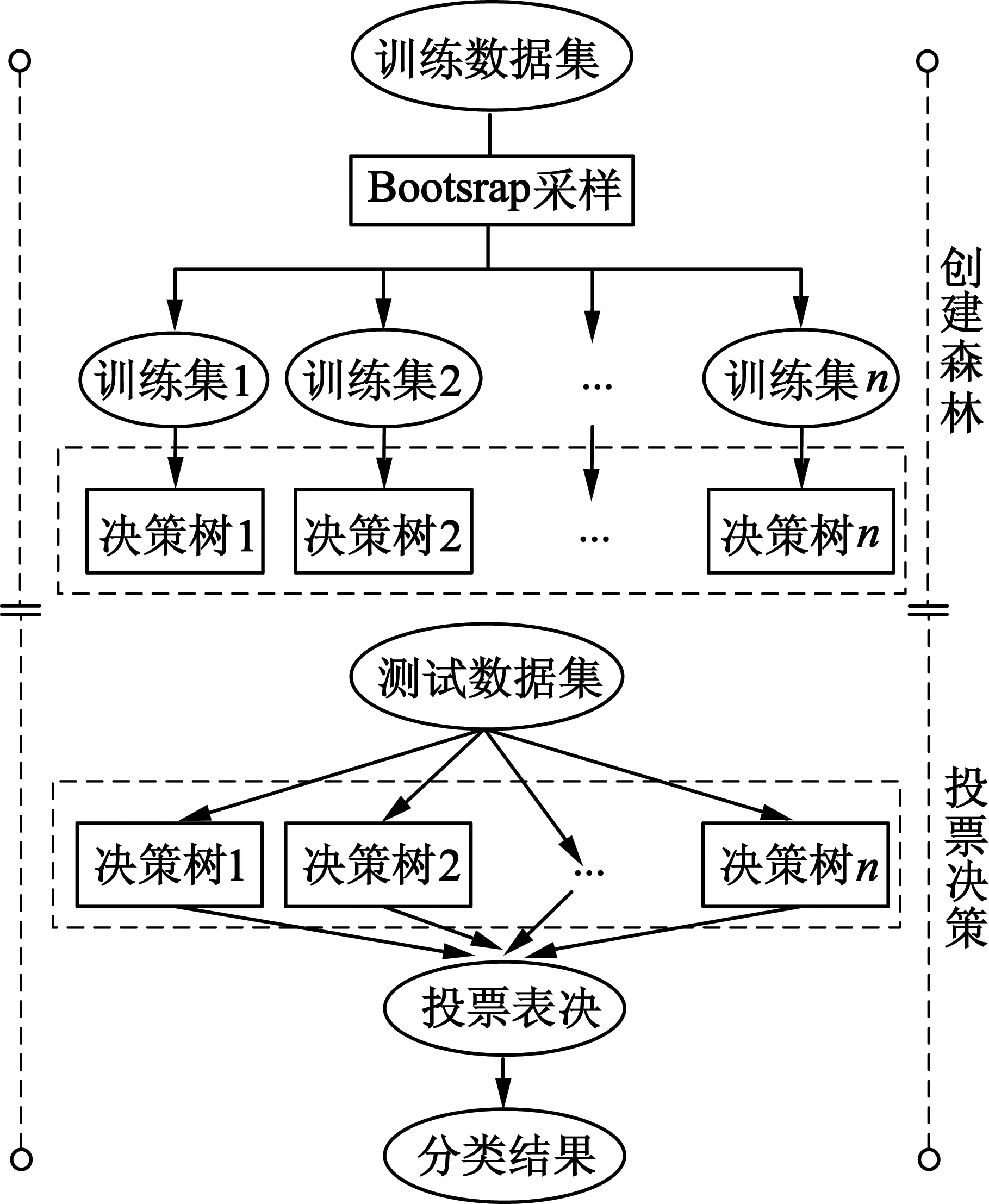
图4 RF算法示意图

以RF为基分类器且个数为3，组合规则为“投票”，那么基于RF的集成分类器结构如图5所示。

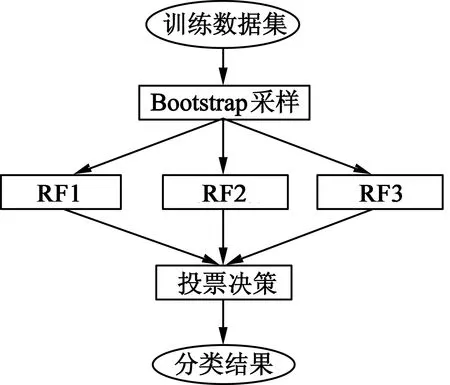
图5 集成分类器示意图

至此，便创建了负载波动下感应电动机转子断条故障诊断模型。由于集成分类器具有多个基分类器，因此在实际工程应用中可以采用多个CPU并行计算，对多个基分类器进行平行运算，从而提高计算速度。

4 实验验证

4.1 故障诊断流程

负载波动下感应电动机转子断条故障诊断流程如下：

1) 采集感应电动机一相定子电压和电流，并进行Hilbert变换，得到复空间矢量电压vs和电流is；

2) 计算电机瞬时功率，并采用低通滤波器滤波得到IAP以及IRP；

3) 经过双Hilbert变换，滤除直流成分；

4) 对IAP，IRP分别进行DWT分解并计算频段能量，提取特征频率所在频段能量Ep和Eq；

5) 以Ep和Eq作为集成分类器输入量训练集成分类器，形成故障诊断模型。

4.2 实验平台

实验用电动机型号为Y90S-4，同步转速为1 500 r/min，极对数为2。表2为电机的具体参数。

表2 实验电动机主要技术参数

负载波动下感应电动机转子断条故障诊断实验平台如图6所示。

(a) 电动机及磁粉制动器

(b) 故障转子

电动机拖动的负载为一台机座式磁粉制动器，其型号为FZ25J，其额定转矩为25 N·m，激磁线圈电压为直流24 V，电流为2.0 A，许用转速为1 500 r/min，冷却方式采用自冷却。

与磁粉制动器配套使用的为一台张力控制器，其具有220 V交流输入，24 V/36 V直流输出，控制方式分为面板控制、外接PLC控制、外接电位器三种控制模式。通过改变控制器的控制信号便可以使磁粉制动器转矩呈现恒定以及波动状态。

恒定负载时，电动机为满载状态；负载波动时，负载波动频率fL为4.5 Hz，波动程度η为2%，此时2sf1约为4.8 Hz。

4.3 实验过程及结果分析

在对电机提取瞬时功率后，我们进一步采用DWT对各个状态下IAP和IRP进行频段分解，并提取各频段能量幅值。由于本文的实验电动机从空载变化到满载状态时，其转子速度变化的大致区间为[1 400，1 490]r/min，因此故障特征频率2sf1的大致分布区间为[0，7]Hz。加之信号采样频率为1 000 Hz，因此本文采用db5小波进行6层分解，并以逼近信号al∈[0,7.8]Hz所在频段能量为故障检测特征量(2sf1，fL均分布于此频段)。

同时，为了凸显故障特征，采用Butterworth低通滤波器对瞬时功率进行滤波之后再进行DWT分解。滤波器的截止频率为10 Hz，阶数为16。

图7为恒定负载下断条故障电机IAP，IRP的FFT频谱图。其中的直流分量已经双Hilbert变换滤除。电压、电流的采样频率为1 kHz。Ap,Aq分别为无功功率和有功功率幅值。由图7可知，IRP中断条故障特征频率2sf1的幅值明显大于IAP中2sf1的幅值。

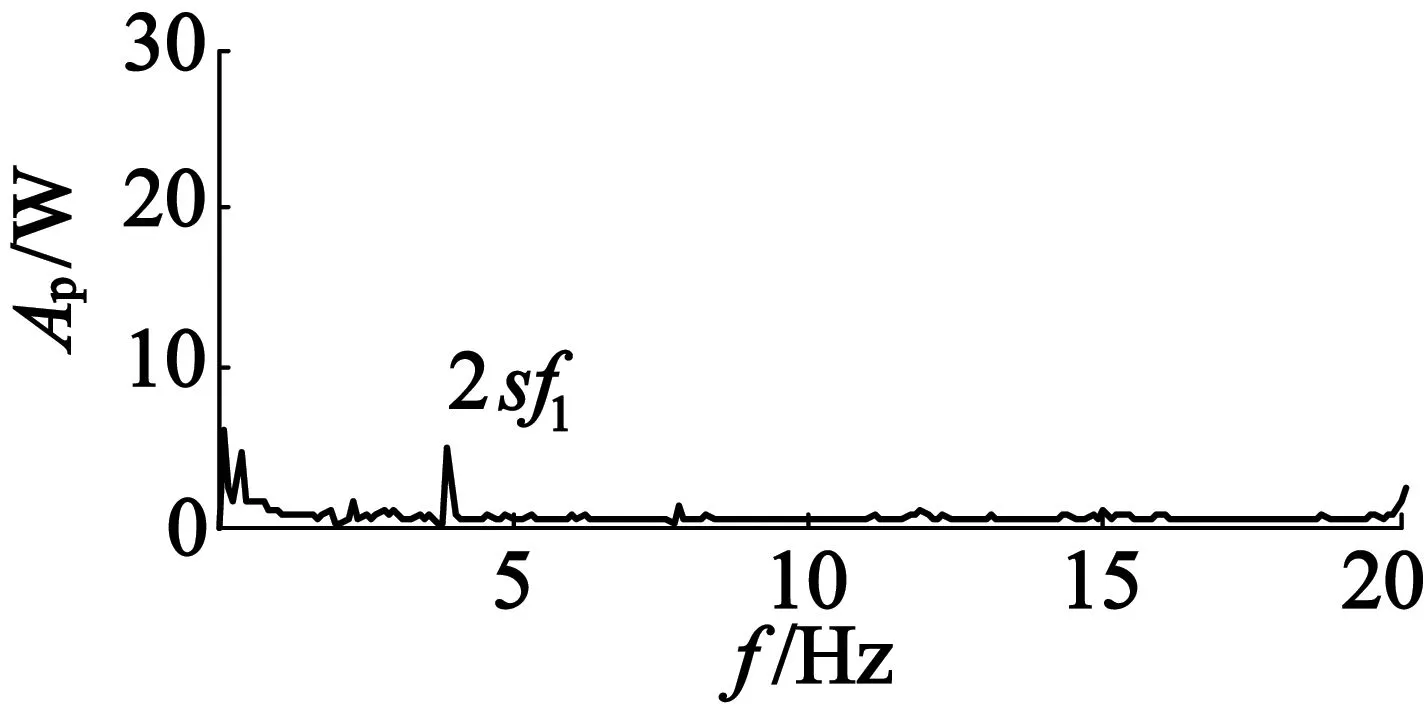
(a) 有功功率频谱

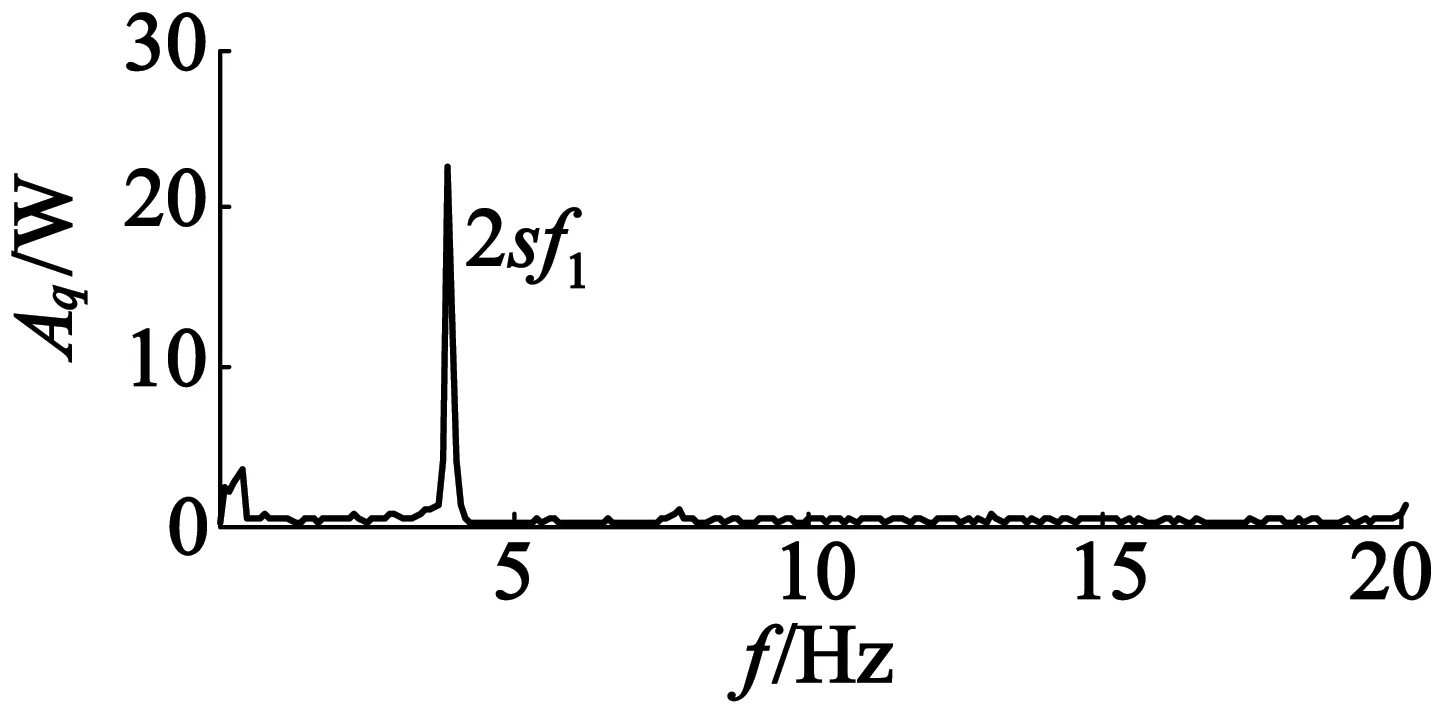
(b) 无功功率频谱

图8为负载波动下转子断条故障电机IAP，IRP频谱图。

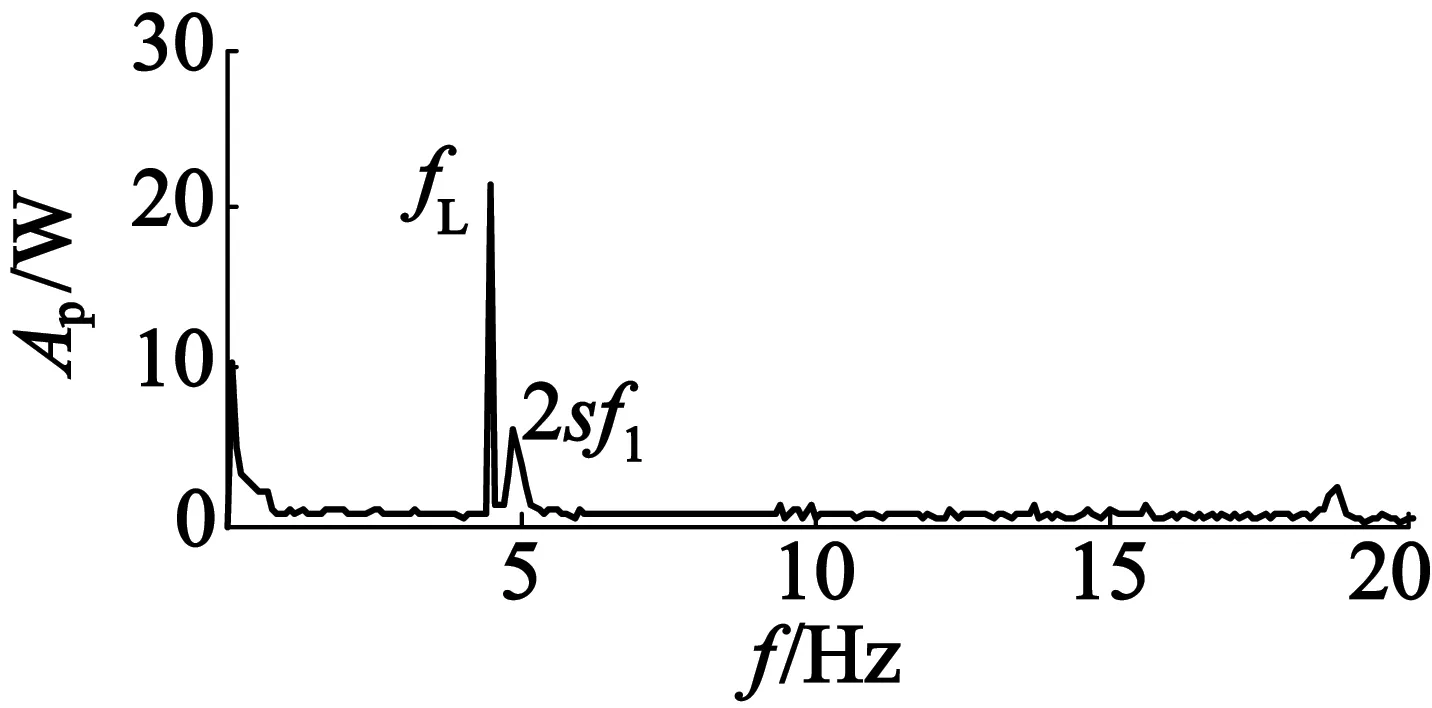
(a) 有功功率频谱

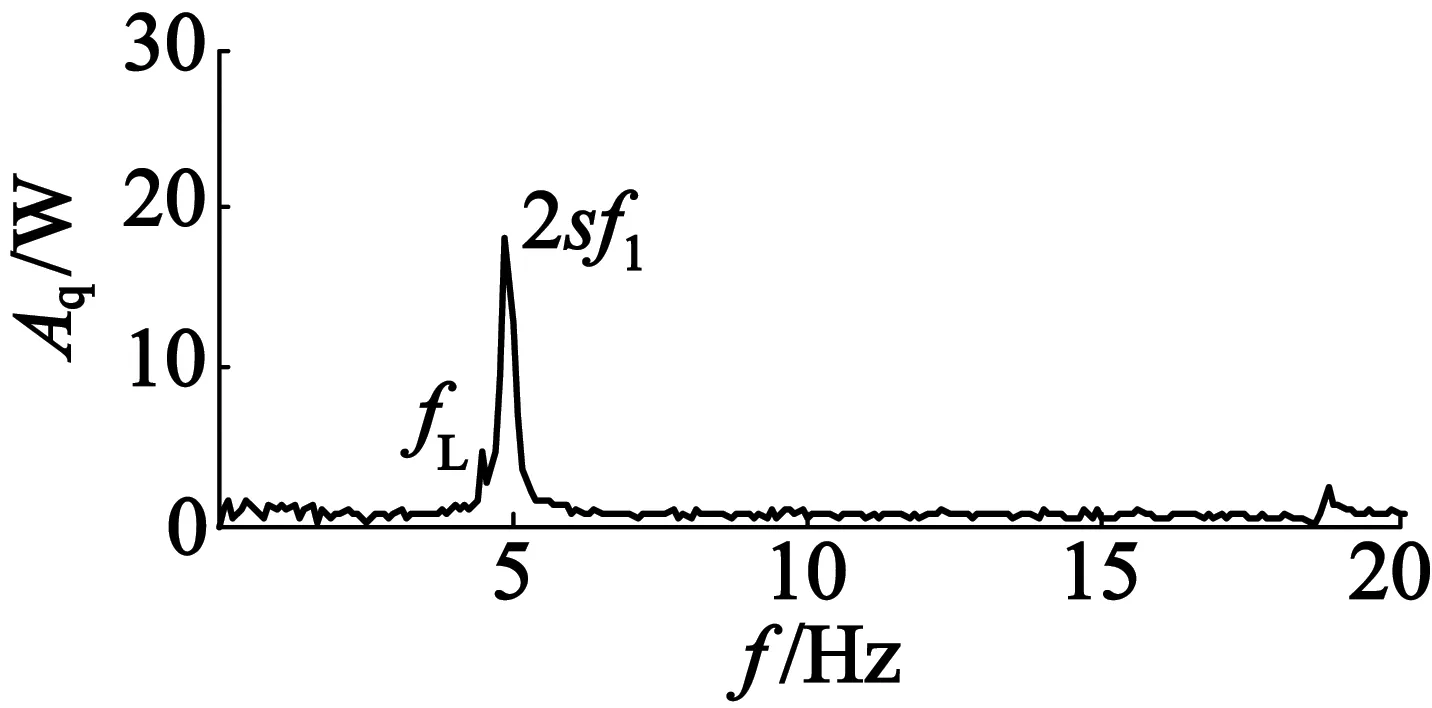
(b) 无功功率频谱

由图8可知，断条故障特征频率2sf1在IRP中的幅值明显大于IAP；而负载波动特征频率fL在IAP的幅值明显大于IRP。由此便可以将负载波动与转子断条故障进行区分。

然后，对不同负载下电机瞬时功率进行DWT分解并提取频段能量，电机瞬时功率小波能量如图9、图10所示。其中频段7为特征频率所在频段。

由图9可知，对于恒定负载，当感应电动机出现转子断条故障时，特征频段7的IRP小波能量幅值明显大于IAP的小波能量幅值。由图10可知，当感应电动机只存在负载波动时，IAP的小波能量幅值明显大于IRP的小波能量幅值；而对于同时存在负载波动与转子断条故障时，频段7的IAP,IRP的小波能量幅值均增大，且大于某一设定阈值。

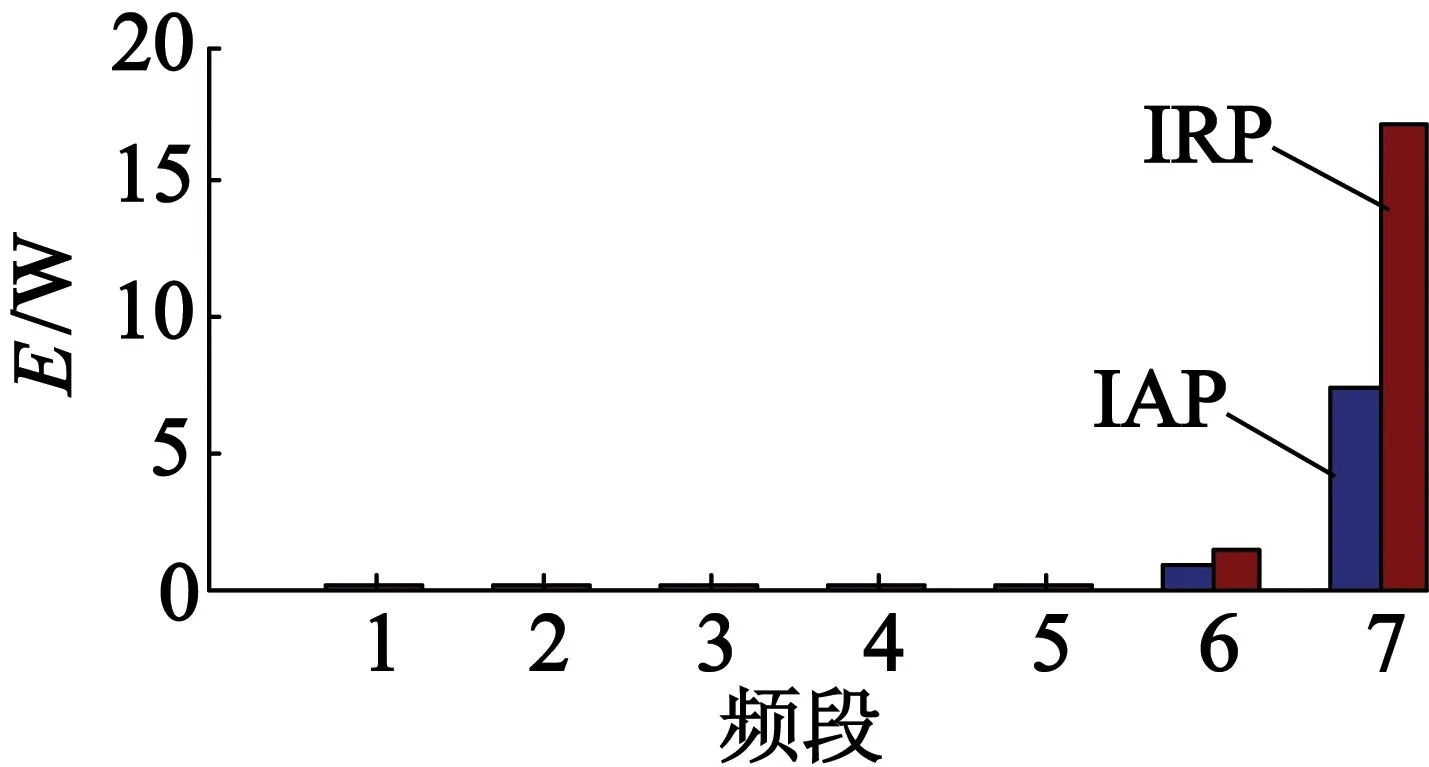
图9 恒定负载转子故障电机小波能量

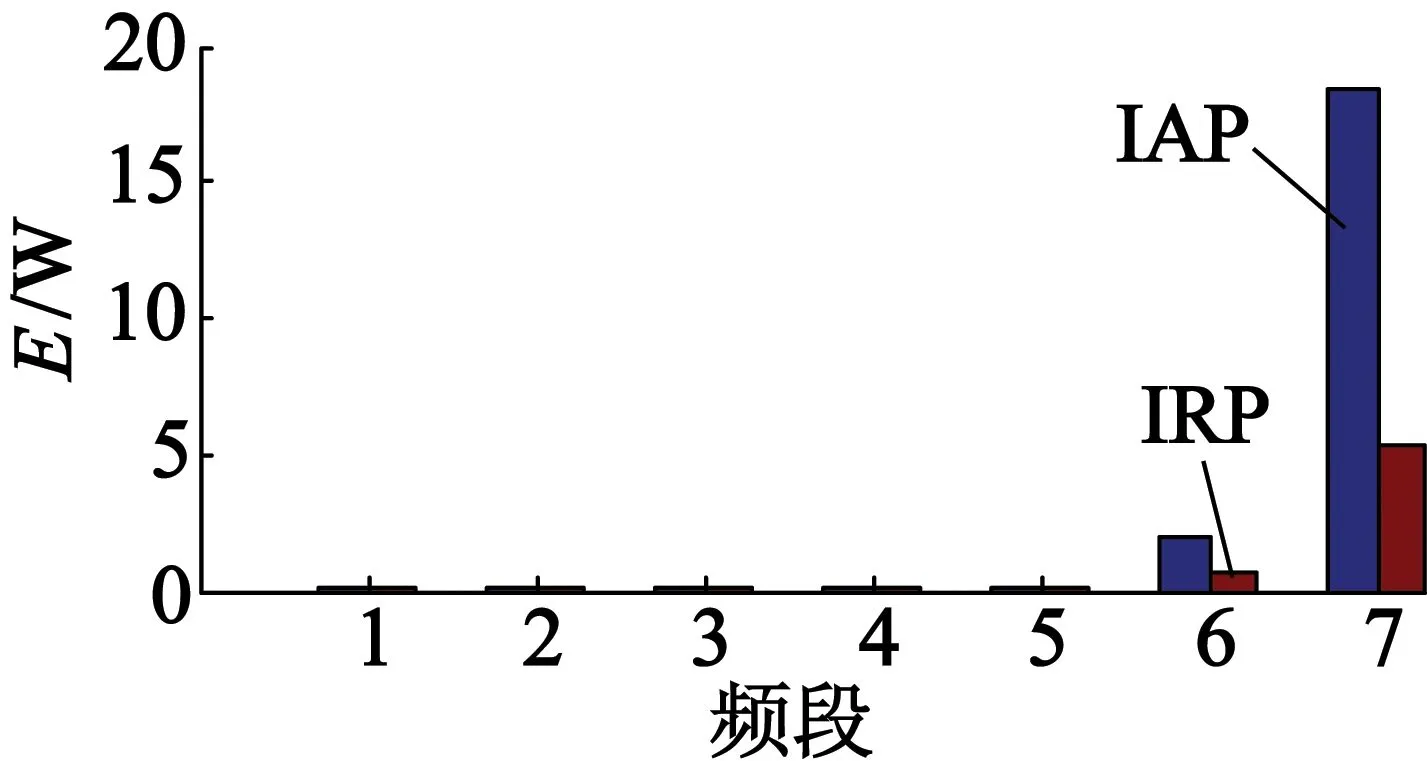
(a) 负载波动正常电机

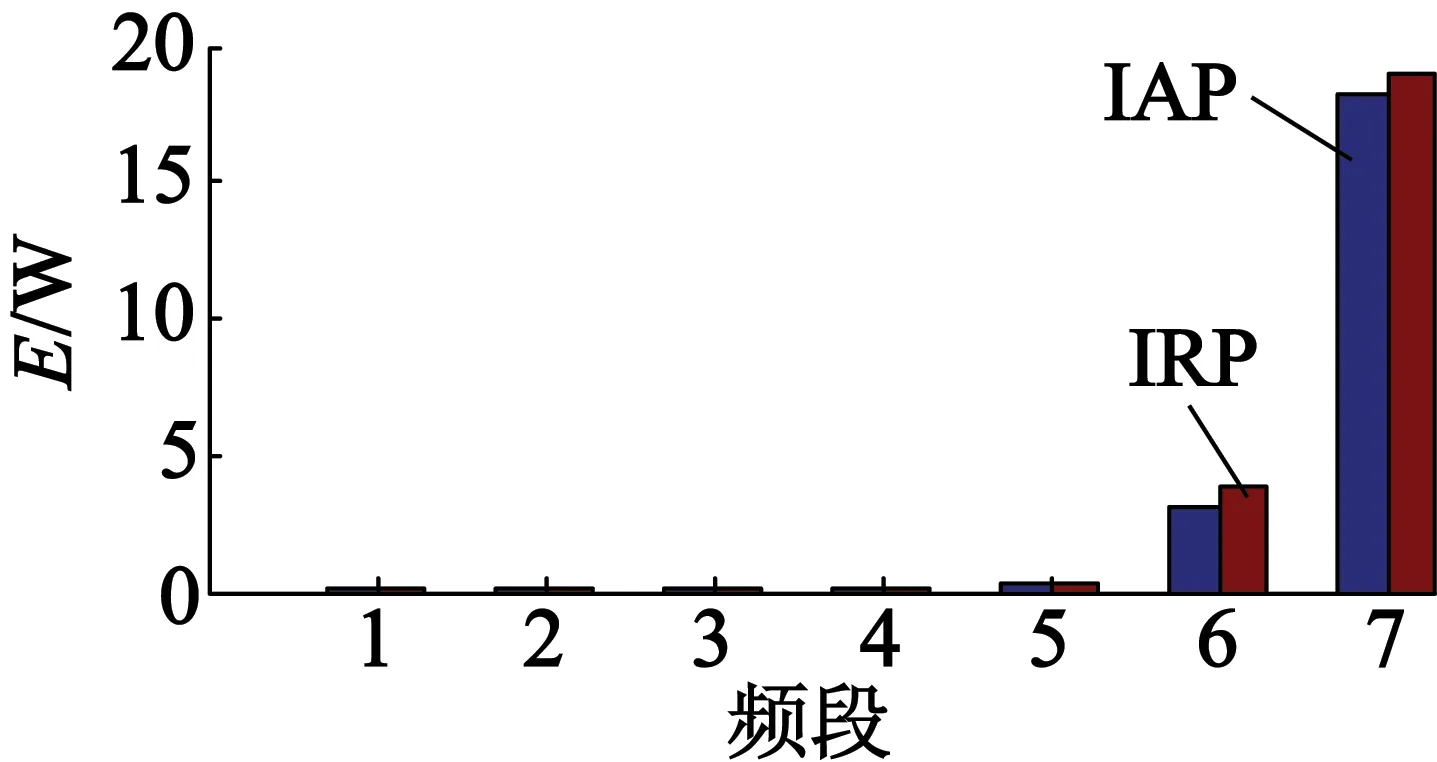
(b) 负载波动断条故障电机

经过DWT提取能量之后，各种状态下特征频段的能量幅值大小如表3所示。

由表3可知，当瞬时功率小波能量出现Ep设定阈值，且Eq>设定阈值，便可以判定电动机同时存在断条故障和负载波动。以上结果验证了本文方法及其新判据的可行性和有效性。

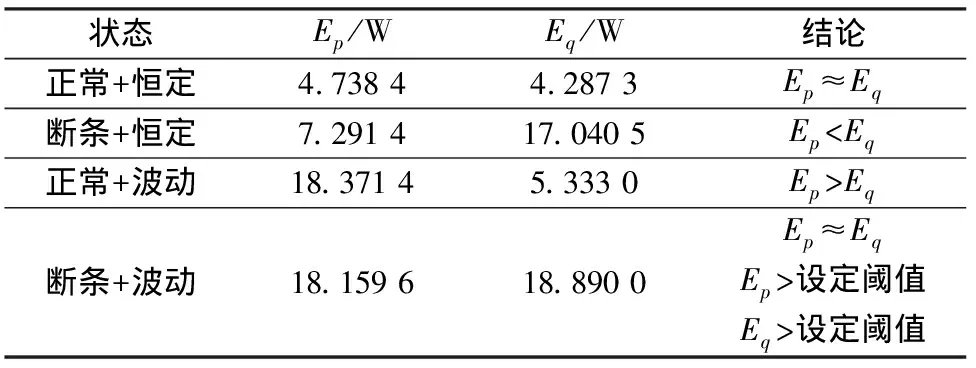
表3 DWT能量幅值

采用本文方法对不同状态电机提取特征向量，选取一部分数据训练集成分类器，形成负载波动下感应电动机转子断条故障诊断模型，剩下的数据作为测试数据集。测试结果如表4所示。

由表4可知，基于集成分类器的负载波动下感应电动机转子断条故障诊断模型具有较高的分类正确率，可以准确识别感应电动机状态。

表4 集成分类器测试分类结果

5 结 语

本文针对负载波动下感应电动机转子断条故障诊断方法进行了研究。

1) 研究了一种负载波动下感应电动机转子断条故障诊断方法并给出了明确有效的诊断判据。

2) 本文方法另辟蹊径，不依赖频谱分析技术，当2sf1与fL非常接近，甚至相同时，亦能对断条故障特征进行准确提取。

3) 引入集成分类器，克服了传统单一分类器分类正确率低的弊端，进一步提高了负载波动下感应电动机转子断条故障诊断精确性。

4) 通过实验验证了恒定负载及波动负载下，该方法对感应电动机转子断条故障诊断的有效性、可行性。