航天回转支撑机构滚子动态特性刚柔耦合分析

江国宝，杨德财，孟凡明*

(1.重庆大学，机械传动国家重点实验室，重庆400044； 2.上海宇航系统工程研究所，上海201109；3.上海市空间飞行器机构重点实验室，上海201109)

1 引言

国际空间站为了提高太阳能电池翼的日光接收面积，通过阿尔法驱动装置(Solar Array Alpha Rotary Joint，SARJ)的连续转动实现对日跟踪[1]。回转支撑机构(Trundle Bearing Assemblies，TBA)作为SARJ 的重要组成部分，其主要作用是在设计寿命期间可靠地连接SARJ 相对旋转的桁架机构P3/S3 与机构P4/S4，并在满足回转精度、摩擦力矩、连续刚度等诸多要求的前提下，提供太阳翼对日定向所需的转动自由度[2]。 现役TBA 机构在工作状态下，结构会因外载荷的动态变化而发生变形，从而导致系统稳定性、精度及寿命下降。此外，机构在运行一段时间后，会出现由于导轨与TBA 轴承表面磨损造成的运动不稳定和驱动困难，甚至无法驱动等问题[3]。

截至目前，国内外一些学者对TBA 回转支撑机构已经做了一定的研究。 Elliot 等[4]对SARJ 在轨工作出现的异常机械振动现象进行了分析，探讨了TBA 轴承单边接触、轴承外表面与滚道摩擦关系及轴承所载荷大小对SARJ系统的影响。 其研究表明SARJ 的异常，极可能是由于滚动接触润滑不良导致的较高TBA轴承单边应力引起。 Christopher 等[5]对空间站TBA 轴承失效问题进行了总结，指出TBA 轴承与导轨间润滑不充分产生的高摩擦力易产生“尖端摩擦”，从而导致轴承与导轨出现磨损。Stuart 等[6]分析了SARJ 产生异常振动现象，指出轴承发生的小程度偏斜会导致轴承边缘产生较高的接触应力，使得轴承与导轨表面遭到破坏。 Curtis 等[7]通过SARJ 地面测试台对SARJ 用TBA 轴承进行油脂修复性能进行测试，发现减小导轨与轴承之间的摩擦系数，可有效抑制引起TBA 轴承严重磨损失效的滚子偏斜和单边接触应力。 Basta 等[8]针对失效TBA 轴承的金相显微结果表明，长时间的工作使得界面间的粘着力增大，最终导致导轨渗氮层的破坏。 Kumar 等[9]针对TBA 轴承进行了结构模态参数变化的灵敏性分析，通过约束优化方法讨论了频率、振型和阻尼系数变化对稳定裕度的影响。

然而上述研究大都集中在TBA 轴承的试验与在轨分析，但TBA 回转支撑机构作为1 个大型运动机构，对其动力学性能研究同样至关重要。 杨承璋[10]通过动力学分析软件ADAMS对空间站TBA 回转支撑机构开展了刚体动力学仿真，讨论了载荷、驱动速度、摩擦系数等因素对该机构动力学性能的影响，但并没有考虑部件弹性变形的作用。 航空航天对部件运动控制精度要求较高，而部件的弹性变形将会对系统的运转精度产生影响，因此弹性变形对TBA 机构动力学性能的影响不应忽略，但国内外学者还鲜有在TBA 回转支撑机构的刚柔耦合动力学方面进行研究。

针对上述问题，本文利用商用分析软件ADAMS 与ANSYS 对TBA 回转支撑机构开展刚柔耦合动力学仿真，分析滚子柔性化、表面摩擦系数、转速和载荷对其的动力学性能影响，以期为TBA 回转支撑机构设计和使用提供理论参考。

2 TBA 三维模型建立

本文所研究的TBA 回转支撑机构可简化如图1 所示，整个TBA 回转支撑机构由TBA 导轨和8 组TBA 组件构成，TBA 组件沿着导轨对称分布。 TBA 回转支撑机构运行时，TBA 组件沿着滚道进行公转，且各个轴承绕着自身回转轴进行自转。

图1 TBA 回转支撑机构简图Fig.1 Sketch of TBA rotary support mechanism

因TBA 组件在导轨上对称分布，故本研究仅对1 组TBA 组件进行研究。 为了能在保证模型原有属性的基础上尽量降低仿真复杂度，将TBA轴承简化为圆柱滚子，并通过三维建模软件Pro/E建立TBA 回转支撑机构三维模型。 机构三维模型如图2(a)所示，在导轨质心处建立总体坐标系e，导轨圆周面在xy 平面，z 轴正方向为竖直向上。 图2b 为TBA 机构三维模型截面图。 由图可知，每组TBA 组件的3 个滚子在左右2 个施力臂的作用下与导轨的3 个表面紧密配合。

图2 TBA 回转支撑机构三维模型图Fig.2 3D model of TBA rotary support mechanism

3 TBA 机构刚柔耦合模型理论

TBA 回转支撑机构中3 个滚子相对导轨运动，滚子与导轨之间的冲击碰撞是机构振动的主要来源。 而部件的柔性变形对碰撞接触有较大的影响，因此将3 个TBA 滚子考虑为柔性体可以提高仿真可靠性。 刚柔耦合建模基本思想是对TBA 机构的各个部件引入局部坐标系，刚体部件的基本位形可表示为局部坐标系相对于总体坐标系e ＝[x，y，z]的浮动，而TBA 机构柔性体部件还需考虑部件内部弹性变形。 各部件通过局部坐标来表示自身位置与方位，其中部件位置表示使用的是笛卡尔坐标el＝[xl，yl，zl](xl为垂直TBA组件运动切向方向，并指向导轨中心的方向；yl为TBA 组件运动切向方向；zl为垂直转动平面并指向导轨接触面方向)。 部件方位描述使用的是欧拉坐标ψ ＝[ψ，θ， b](ψ 为x 与xl夹角；θ 为y 与yl夹角；b 为z 与zl夹角)。 柔性体的弹性变形的描述是使用模态坐标q ＝{q1， q2，… qM}(qi为第i 阶模态坐标)，TBA 回转支撑机构柔性体部件广义坐标可写成ξ ＝[e，ψ，q]T。 TBA 机构中，柔性体部件内任意结点P 在总体坐标中的位置可表示为式(1)～(2)[11]。

式中：r0为TBA 机构柔性体部件局部坐标系原点在总体坐标系中向量；A 为TBA 机构柔性体部件局部坐标系与总体坐标系的变换矩阵；sp为TBA 机构柔性部件结点P 未变形时位移向量；up为TBA 机构柔性部件结点P 瞬态变形向量； Φp为TBA 机构柔性部件结点P 的变形模态矩阵。式(1)对时间进行求导，则TBA 机构柔性部件上结点P 速度可表示为式(3)。

式中：r·为TBA 机构柔性体部件局部坐标系原点在总体坐标中的位置向量的时间导数；为TBA 机构柔性部件结点P 的瞬态变形向量的时间导数；为TBA 机构柔性体部件局部坐标系到总体坐标系的变换矩阵的时间导数。TBA机构柔性部件上结点P 的角速度可表示为式(4)所示刚性部分角速度与变形引起的角速度之和。

式中：mp和Ip分别为TBA 机构柔性部件结点P 的模态质量与转动惯量。 TBA 机构柔性部件势能可表示为式(6)所示，由重力势能和弹性势能构成。

式中：Vg为重力势能；K 为结构单元相对于模态坐标q 的广义刚度矩阵。 运用拉格朗日乘子法可建立TBA 机构系统的动力学方程如式(7)[12]。

式中：L 为拉格朗日函数；Q 为广义坐标ξ 方向的广义力；ψ 为TBA 机构柔性部件的约束方程；Γ 为TBA 机构柔性部件能量耗散函数。 TBA组件在驱动力的作用下沿着导轨运行，运行过程中的滚子与导轨，以及TBA 组件内部会由于摩擦而造成驱动力的损失与能量损耗。 因此，当TBA组件沿着导轨匀速转动，TBA 组件的力矩可表示为式(8)～(9)。

式中：MR为滚子与导轨间摩擦力矩；MW为滚子与滚子轴间摩擦力距；Fxi为滚子i 与导轨间法向接触力；Fdi为为各滚子与滚子轴法向接触力；Ri为滚子i 半径；Rdi为滚子轴i 半径；μ 为滚子与导轨间静摩擦系数；μd为滚子与滚子轴间静摩擦系数。 滚子在导轨表面运转时，会受到来自导轨与滚子轴的摩擦力矩，与导轨接触产生的摩擦力矩使滚子有着转动的趋势，与滚子轴接触的摩擦力矩会对滚子转动有着阻碍效果。 当MW＜MR时，滚子相对于滚子轴转动，即滚子与导轨之间为无滑动运动；当MW≥MR，则滚子相对于滚子轴静止，即滚子与导轨之间产生滑动运动。 由经典库伦理论可得，驱动滚子所消耗的能量速率为式(10)。

式中：μr为滚子与滚子轴间动摩擦系数；μ0为滚子与导轨间动摩擦系数；ω 为TBA 组件驱动转速；ωi为滚子i 转速，i＝1，2，3。

4 求解流程

在ADAMS/Flex 模块中可对模型进行柔性化处理，但只适用于结构较为简单的模型，而在ANSYS 中对模型进行柔性化处理则更为便捷。 在Pro/E 中完成对TBA 机构三维模型的建立后，将TBA 滚子模型输入至ANSYS 中进行有限元模型的创建。

实际TBA 机构轴承外圈的材料为不锈钢G95Cr18，根据该材料实际特性，在ANSYS 前处理中对TBA 滚子的材料属性定义如下：弹性模型E＝206 GPa，泊松比v＝0.3，密度ρ ＝7.9×103kg/m3。选择用于构造三维固体结构的8 节点Solid185 单元对模型进行网格划分。

完成网格划分后，需要在TBA 滚子上建立外部节点和刚性区域，外部节点和刚性区域是用于在ADAMS 中对滚子施加约束和驱动。 最后利用ANSYS 后处理中的ADAMS 连接口输出滚子模态中性文件，用于在ADAMS 中替换刚体部件。 TBA滚子柔性体的节点信息、刚度、质心、频率等基本信息均被包括在模态中性文件中。

将3 个TBA 滚子的模态中性文件输入至ADAMS 中，替换原有模型中的刚性TBA 滚子，并对模型添加部件材料属性与运动副等约束后，施加的约束类型及其对象如表1 所示，图3 为施加约束后的模型。

完成运动副的定义后，在左右两个施力臂质心处施加方向平行于导轨上接触面的载荷F，并对TBA 组件施加驱动，使之沿着导轨进行旋转。滚子与导轨之间施加碰撞接触，具体仿真参数见表2 所示，若无特殊说明这些参数不变。

表1 约束设置Table 1 Constraint settings

表2 仿真输入参数Table 2 Input parameters of simulation

图3 施加约束后TBA 模型Fig.3 TBA Model with imposed constraints

5 仿真结果分析

5.1 柔性的影响

基于相同参数分别对TBA 回转支撑机构进行刚体动力学仿真和刚柔耦合动力学仿真，研究TBA 滚子柔性化对TBA 组件动力学的影响，仿真参数见表2。 由于TBA 机构中上滚子所受载荷较大，滚子偏斜也多集中于上滚子(即滚子1)，因此主要针对上滚子仿真结果进行讨论。 刚柔耦合模型与刚体模型仿真结果下，上滚子与导轨之间法向(z 轴)接触力对比如图4 所示。 刚柔耦合结果的上滚子与导轨间法向接触力的波动范围明显减小，这与柔性体模型特征相符合，显示了柔性体的阻尼性质对部件间的冲击振动有着一定的缓冲效果。文献[13]得到了类似的结论。

图5 为上滚子质心位置在法向的波动范围对比。 由图可知，相对于上滚子初始位置，柔性体上滚子质心位置波动范围相比于刚体上滚子更偏向于z 轴负方向，也就是更接近在z 轴负方向的导轨表面。 原因可归结于波动范围较大的法向接触力对上滚子的作用与柔性体部件产生的变形，使得刚柔耦合模型上滚子质心产生更大的位移。 因而在考虑柔性部件情况下，TBA 机构运动特性更符合实际情况。

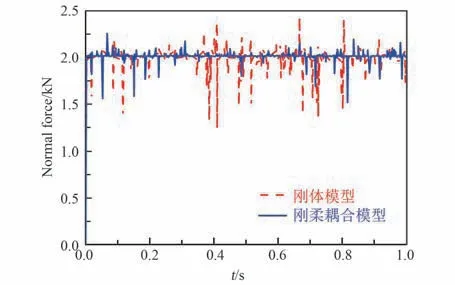
图4 刚柔滚子与导轨之间法向力对比Fig.4 Comparison of normal force between rigidflexible upper roller and guide rail

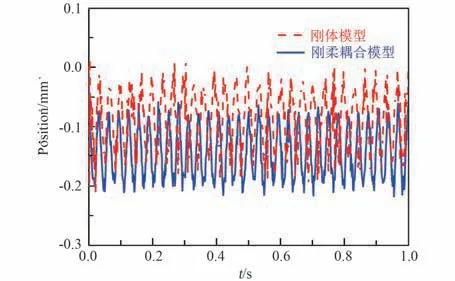
图5 刚柔上滚子质心法向位置对比Fig.5 Comparison of normal position of center of mass in rigid-flexible upper roller

5.2 摩擦系数的影响

对滚子柔性化处理后的TBA 回转支撑机构进行刚柔耦合动力学仿真，仿真参数见表2。 根据实际TBA 滚子承寿命试验结果，TBA 滚子与导轨之间摩擦系数在0.1～0.6 之间，因此分别设置静摩擦系数μ 为0.2、0.3 及0.5，动摩擦系数μ0分别为0.15、0.22 及0.3，进行动力学仿真分析。不同摩擦系数下，上滚子与导轨之间法向接触力、径向及切向摩擦力如图6 所示。 由图6(a)可见，上滚子与导轨间法向接触力均在施加载荷2000 N附近波动，波动幅度随摩擦系数的增加而变大。由图6(b)可知，上滚子之间的径向摩擦力在零点上下波动，波动幅值亦随摩擦系数的增大而增大。由图6(c)可知，上滚子与导轨直切向摩擦力随着摩擦系数的增大而上升，基本与滚子导轨间动摩擦系数成正比，因此可判断导轨与滚子间存在着相对滑动。

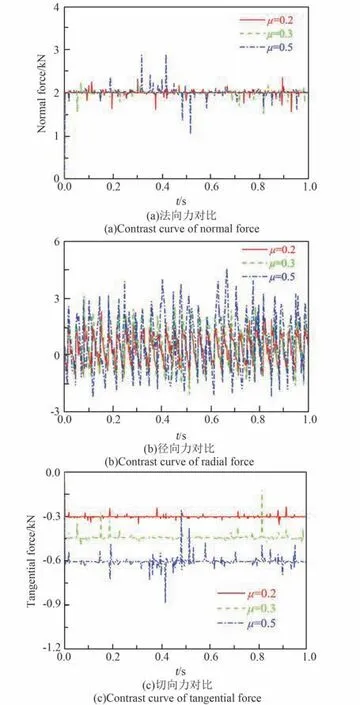
图6 不同摩擦系数下上滚子各方向接触力对比Fig.6 Comparison of contact force in each direction of upper roller under different friction coefficients

图7为不同摩擦系数下的上滚子von Mises应力分布图。 从图中可知，当静摩擦系数分别为0.2、0.3 和0.5 时，上滚子的最大应力分别为32.49、35.16 与38.23 MPa，上滚子的应力最大值随着摩擦系数增加而增大。 文献[14]也得出类似结论，这是由于较大的摩擦系数会增大摩擦力幅值与法向力波动范围，从而使得von Mises 应力增大，较大的应力会使得TBA 轴承的使用寿命缩短。 因此在TBA 机构的设计中，应尽量保证TBA轴承与导轨之间的摩擦系数在一个较低的水平。

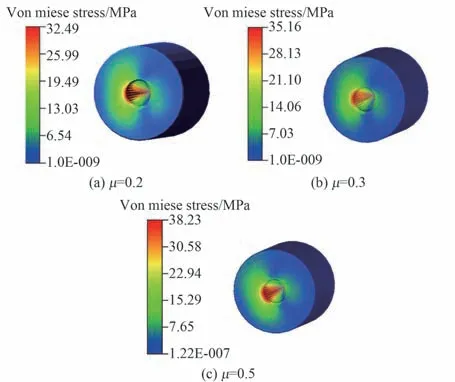
图7 摩擦系数对上滚子von Mises 应力分布的影响Fig.7 Von Mises stress distribution in upper roller under different friction coefficients

5.3 驱动速度的影响

TBA 回转支撑机构运转过程中，不同的在轨时期TBA 组件驱动速度有所不同，而不同的驱动速度对机构的振动、部件受力及运转稳定性将会产生影响。 因此在驱动转速为n ＝2π、4π 及10π rad/s下，对TBA 机构进行动力学仿真分析，图8 为不同驱动速度下，刚体模型结果与刚柔耦合模型结果中上滚子与导轨之间的平均法向接触力对比，由图8 可知，两种模型下，上滚子与导轨间的法向接触力均随着TBA 组件驱动速度的增加而增大，但刚柔耦合结果下的上升速率大于刚体结果。 在转速n ＝2π、4π 及10π rad/s 时，与刚体模型相比，刚柔耦合模型下的上滚子与导轨在法向接触力分别下降11.9%、下降2.3%与增大15%，可见，驱动速度对刚柔耦合模型的影响层度较大，因此在实际应用中需要适当控制TBA 轴承组件的驱动速度，以免较大的接触力造成滚子与导轨接触面的破坏。

图9 为驱动速度分别为2π、4π 及10π rad/s下，刚柔耦合结果下的上滚子上最大von Mises 应力对比。 由图可见，上滚子的最大应力随着驱动速度的增加而减小，最大应力同样出现在TBA 上滚子内表面，出现在这种现象的原因归咎于上滚子与导轨之间较大的接触力使得滚子与滚子轴之间压力有所下降，从而使得von Mises 应力减小。

图8 不同驱动速度下刚柔耦合与刚体上滚子法向接触力对比Fig.8 Comparison of average normal contact force in upper roller between rigid model and flexible model at different driving speeds

图9 不同驱动速度下上滚子最大应力对比图Fig.9 Comparison of maximum von mises stress in upper roller under different driving speeds

图10为不同驱动速度下的上滚子质心法向加速度3D 频谱。 由图可见，当TBA 组件的驱动速度增加时，上滚子的法向振动加速度幅值基本保持一定。 振动加速度的最大振动频率随着转速的增加而增大，当驱动速度分别为2π、4π 及10π rad/s 时，波动频率最大值分别为332.4、358.9 与398.5 Hz，出现这种现象的原因为较大的驱动速度，增大了上滚子与导轨接触碰撞的频次，从而增大了上滚子在法向的振动频率。

5.4 载荷的影响

TBA 回转支撑机构运转过程中，对施力臂施加载荷的大小将影响机构整体刚度与运转精度，且将影响TBA 滚子的使用寿命，因此需对其进行研究。 在机构左右施力臂质心处分别施加载荷F ＝1000、2000 及3000 N，进行动力学仿真分析。图11 给出了考虑部件柔性化下，不同载荷下上滚子质心在法向位置波动对比图。 由图可见，改变施加在左右施力臂上载荷时，上滚子质心在法向的位置波动范围发生了变化，且随着载荷的增大，质心位置靠近z 轴负方向(导轨表面)。 相对于上滚子初始位置，平均位移值分别为0.116、0.135和0.151 mm，原因可归于弹性变形使得上滚子质心靠近导轨表面。

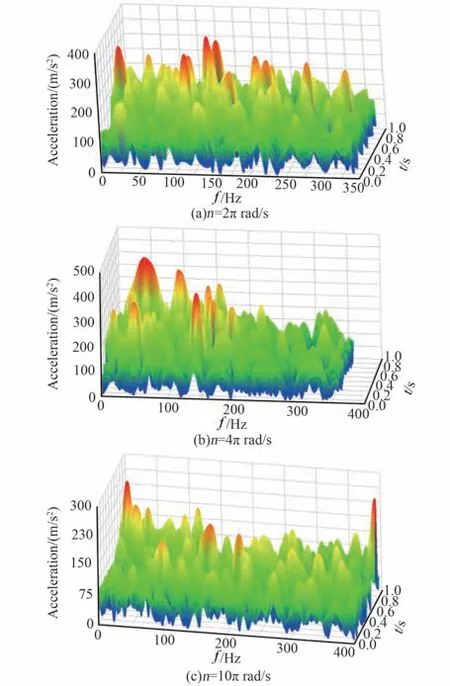
图10 不同驱动速度上滚子法向振动加速度3D 频谱图Fig.10 Comparison of 3D spectrum chart of normal vibration acceleration in rigid-flexible upper roller under different driving speeds

图12给出了不同载荷下，上滚子质心在法向上的加速度的对比曲线。 由图可知，当其他变量固定时，上滚子在法向上的振动加速度波动范围随着施加载荷的增加而降低，其原因可归结于施力臂上施加的载荷使得TBA 组件具有更大的刚度，滚子产生弹性变形，并且较大的载荷对滚子振动的抑制作用，使得其具有更稳定的运动状态。

图11 不同载荷下刚柔上滚子质心法向位置对比Fig.11 Comparison of normal position of center of mass in rigid- flexible upper roller under different loads

图12 不同载荷下刚柔上滚子法向加速度对比Fig.12 Comparison of normal acceleration in rigidflexible upper roller under different loads

图13为不同载荷下，刚柔耦合结果与刚体结果下驱动大滚子所消耗能量速率对比。 由图可见，随着作用在施力臂上载荷的增加，驱动上滚子所消耗能量的速率增大，且刚柔耦合结果下驱动大滚子所消耗能量速率小于纯刚体结果，但随着载荷的增加，差距有所减小。 当载荷F ＝1000、2000 及3000 N 时，相比于刚体，刚柔耦合结果驱动上滚子的能量消耗速率分别下降16.53%、12.69%及3.97%，由图4 可知，滚子柔性化后会减小上滚子与导轨之间法向接触力，从而使得上滚子与导轨间摩擦力相应减小，相应地驱动上滚子所消耗的能量减少。

6 结论

1)刚柔耦合模型相对于纯刚体模型，上滚子与导轨之间的接触力的波动范围降低，上滚子质心位置的波动范围有着一定的减小。

2)随着TBA 滚子与导轨之间不同摩擦系数的增加，上滚子与导轨之间的摩擦力幅值与摩擦力波动范围均增大，上滚子最大von Mises 应力与也增大。

图13 不同载荷下上滚子平均能量消耗速率对比Fig.13 Comparison of average power loss rate in rigid-flexible upper rollers under different loads

3)随着TBA 组件驱动速度的增加，上滚子与导轨之间平均法向作用力与上滚子质心的振动频率均有所增大。

4)本文得到的结果，可为TBA 回转支撑机构的整体性能准确分析提供了一定的理论参考。

参考文献(References)

[1]Timothy L K，Justin P E，Michael J D.Roller testing to mimic damage of the ISS SARJ ring and durability test to simulate fifteen years of SARJ operation using the damaged surface[R].NASA/TM-2016-218958， 2016.

[2]胡鹏.阿尔法新型传动机构设计及试验研究[D].重庆：重庆大学， 2016.Hu P.Design and Research on a New Transmission Mechanism in Alpha Rotary Joint[D].Chongqing： Chongqing University， 2016.(in Chinese)

[3]Taylor D， Enriquez C， Mccann D， et al.Root cause investigation of the starboard Solar Alpha Rotary Joint anomaly on the International Space Station[C]/ /Proceedings of 40thAerospace Mechanisms Symposium.Florida， United States： NASA JSC-CN-18874， 2010.

[4]Elliot P H， Justin M， Daniel J S， et al.The International Space Station Solar Alpha Rotary Joint anomaly investigation[C]/ /Proceedings of 40thAerospace Mechanisms Symposium， Florida， United States： NASAJSC-CN-19606， 2010：187-206.

[5]Christopher D， Timothy L K， and Michael J D.ISS Solar Array Alpha Rotary Joint (SARJ)bearing failure and recovery：technical and project management lessons learned [R].NASA/TP—2011-217116， 2011.

[6]Stuart L， Curtis A， Carter R， et al.Space station solar array joint repair[C]/ /ASTM International Rolling Element Bearings Conference.Anaheim： NASA， 2015.

[7]Curtis A， Will W， Stu L.Test validation of the repair to the Space Station Solar Alpha Rotary Joint[C]/ /Proceedings of 40thAerospace Mechanisms Symposium， Florida， United States： NASA NASA/CP-2010-216272， 2010：207-218.

[8]Basta E A， Rajib D， John F， et al.Solar Alpha Rotary Joint anomaly： the materials ＆ processes perspective[R].JSC-18189， 2009.

[9]Kumar R R， Cooper P A， Lim T W.Sensitivity of Space Station Alpha Joint robust controller to structural modal parameter variations[J].Journal of Guidance Control ＆ Dynamics，1991， 15(6)：1427-1433.

[10]杨承璋.二硫化钼涂层摩擦学性能及其在TBA 轴承上的应用[D].重庆： 重庆大学， 2018.Yang C Z.Tribological Properties of MoS2Coating and its Application in TBA Bearing[D].Chongqing： Chongqing University， 2018.(in Chinese)

[11]刘成武.大型压缩机动力学分析与噪声预测[D].南京：南京理工大学， 2006.Liu C W.Dynamic Analysis and Noise Prediction of the Large-Scale Cssor[D].Nanjing：Nanjing University of Science and Technology， 2006.(in Chinese)

[12]李宽.内燃叉车动力学仿真与振动控制关键技术研究[D].桂林：桂林电子科技大学， 2017.Li K.Research on Key Technology of Dynamic Simulation and Vibration Control of Internal Combustion Forklift[D].Guilin：Guilin University of Electronic Technology， 2017.(in Chinese)

[13]宁少慧， 武学锋.刚柔耦合的齿轮传动系统动力学特性分析[J].机械工程与自动化， 2015(6)：64-66.Ning S H， Wu X F.Rigid-flexible coupling dynamic characteristics and analysis of gear transmission system[J].Mechanical Engineering ＆ Automation， 2015(6)：64-66.(in Chinese)

[14]张瑾.大柔性太阳帆航天器姿轨耦合动力学与控制研究[D].北京：清华大学， 2013.Zhang J.Research on the Coupled Attitude-Orbit Dynamic and Control of the Large Flexible Solar Sail Spacecraft[D].Beijing： Tsinghua University， 2013.(in Chinese)

[15]张凯.磁头/磁盘界面摩擦学特性影响因素分析及实验研究[D].哈尔滨：哈尔滨工业大学， 2015.Zhang K.Analysis and Experimental Research on Influencing Factors of Tribological Properties of Head Disk Interface[D].Harbin： Harbin Institute of Technology.2013.(in Chinese)

[16]张永德， 汪洋涛， 王沫楠，等.基于ANSYS 与ADAMS 的柔性体联合仿真[J].系统仿真学报， 2008， 20(17)：4501-4504.Zhang Y D， Wang Y T， Wang M N， et al.Co-simulation of flexible body based on ANSYS and ADAMS[J].Journal of System Simulation， 2008， 20(17)：4501-4504.(in Chinese)

[17]赵静， 柳宁， 吴斌，等.中性浮力和失重环境人体运动仿真比较研究[J].载人航天， 2014， 20(6)：517-519.Zhao J， Liu N， Wu B， et al.Human motion simulation comparison research between neutral buoyancy and weightless environment[J].Manned Spaceflight， 2014， 20(6)：517-519.(in Chinese)

[18]梅菊， 黄松和， 李超军.基于ADAMS 与ANSYS 的凸轮连杆长摆臂系统的刚柔耦合分析[J].包装工程， 2016，37(7)：103-106.Mei J， Huang S H， Li C J.Analysis of rigid-flexible coupling CAM system with long swing rod based on ANSYS and ADAMS[J].Packaging Engineering， 2016， 37(7)：103-106.(in Chinese)