数学解题教学策略对学生非智力因素的影响
韩丹丹
摘 要:解题教学是数学教学的“生命线”,生动、活泼的教学策略可以激起学生的好奇心,从而唤醒深层的探索欲望.在解题教学中教师可以通过通关法、分解法、考点法等方法来影响学生的非智力因素,从而提高学生的解题能力.
关键词:解题教学;通关法;分解法;考点法;非智力因素


依托上述四个模块再回到本题中,知识间的建构体系很快完成,学生很自然地分类讨论:
①当P在CD延长线上时,问题转化为分解部分(3)的模型,答案为[∠γ=∠α+∠β];
②当P在 DC延长线上时,问题转化为分解部分(4)的模型,答案为[∠α=∠β+∠γ].
分解法使学生清晰认識到从整体到部分的拆分以及从部分到整体的融合,充分感受知识结构间的网状效应,深刻理解知识点的内涵和外延,让学生在对事物的认识上经历由合到分、由分到合的完整过程,不仅快速、高效、轻松地解决此题,而且对培养转化与化归的数学思想是一个良好的契机.
三、考点法引领学生揣测出题动机
考点法是从心理学科出发引导学生揣摩命题人的出题意向,提炼出考点及考查方向,以换位思考的方式深度激发思维能力,达到深入教学、深入钻研的目的.
例 如图6,[BC]是[∠ABD]的平分线,[∠ABC=30]°,[AB⊥AC],[P]为[BC]边的中点,[PB=PD]. ①求证:四边形[APDC]为菱形;②四边形[APDC]可能为正方形吗?③若[△PCD]沿[PD]边折叠,使点[C]落在点[C']处,[PC']与[BD]边交于点[F],求证:[PF⊥BD].
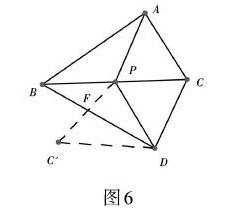
这是一道很普通的几何问题,但由于条件多、繁,学生很难理清头绪,畏难情绪瞬间滋生,教师可通过引导学生猜测出题人的意图寻求线索,出示如下内容:
考点1:____________,由此联想到____________;
考点2:____________,由此联想到____________;
考点3:____________,由此联想到____________;
考点4:____________,由此联想到____________;
……
这样互换位置的研究方式可以刺激学生的直觉动机,挖掘主动的本能,毕竟人人都想体验“高高在上”的感觉.学生会联想到角平分线性质、等边三角形特点、直角三角形性质……通过这些成品的再加工、精练,锻造出本题的解决方案.在“联想网络”的综合传递下,大脑会将各部分知识进行糅合、提炼、整合,从而顺利解决问题.
引导学生站在命题人的立场深刻剖析考点的来源背景和生成过程,这种触及心灵深处的学习,有利于将各部分知识点进行架构,把握出题思路,品味答题角度,捕获解题规律,完善解决方法,从而将知识结构深入骨髓,内化为大脑最深层领域,填补最近发展区,也是自学方式的最高境界.
著名教育家第斯多惠说:教学的艺术不在于传授本领,而在于激励、唤醒和鼓舞.在以上教学模式的尝试下,学生对数学的畏难情绪明显降低,后进生对数学的好感与日俱增,优等生的高品质思维水平更加凸显,数学课氛围活泼生动、你追我赶,奇妙的思维火花多次在数学课上闪耀,学生的解题能力大有提高.但以上策略还需细化、优化:
1.通关法的题目难度不能过大,不能在开始就被吓退,关卡要由易到难,层次分明,保证全体学生参与其中,通关结束后可评选“通关小达人”作为激励.
2.分解法要注意各环节的位置顺序及相互间的内在联系,防止机械、无重点的划分,要与完整教学法交替使用.
3.考点法是深入学习的一种方式,起初可以以小组讨论共享思想的模式进行.

