贸易战背景下的中美贸易研究

高一凡

【摘 要】 本文从2018年3月初至今的中美貿易战入手，通过研究世界银行统计数据，建立演化博弈模，分析雅可比矩阵与均衡点稳定性及变量。研究发现中美双方选择继续合作所能够获得的合作收益越多，中美双方越趋向于选择合作策略;合作成本值越小，单独一方选择竞争而另一方选择合作给选择竞争一方的收益越小，单独一方选择合作而另一方选择竞争使选择合作一方的损失越小中美双方越趋向于选择继续合作策略。通过研究，本文验证了中美贸易的重要性，中美双方应结束贸易战，继续贸易合作并建立有效的保障机制。

【关键词】 中美贸易战 贸易关系 动态演化博弈 鞍点

一、引言

2018年3月美国总统特朗普在白宫签署了对中国输美产品征收关税，在这之后的一年内，中美双方在贸易问题上始终不能达成共识，结束贸易摩擦。

根据世界银行的贸易数据统计，自2000年至2016年，中国对美出口贸易总额一直稳步上升，但出口美国贸易总额占中国出口总额比值稳中有降，在2015年和2016年有所上升，但一直在20%上下徘徊。基于此得出，美国是中国最重要的出口贸易国，比率虽然有所下降，但20%的比重极大。

自2000年至2016年，美国对中出口贸易总额也是一直稳步上升，同时出口中国贸易总额占美国出口总额比值稳步上升，在2016年，比值有所下降。近几年基本趋于稳定在10%左右的水平。基于此得出，中国是美国重要的出口贸易国。美国出口中国的贸易额在美国出口总额中比重没那么大，但10%比重的体量相对美国的贸易总额十分庞大。中美双方如继续扩大贸易摩擦，对美方的贸易出口也会造成重大影响。

二、模型建立与分析

（一）理论模型

演化博弈策略于1973年英国进化生物学家约翰·梅纳德·史密斯提出，后来演化博弈的相关理论就被广泛应用到经济学领域。演化博弈论的核心是演化稳定策略和复制动态方程，分析过程中将博弈理论和动态演化过程。

若s*是一个演化稳定策略（ESS），则s*构成一个纳什均衡，对任意的s，有u（s*，s*）≥u（s*，s）。如果s*≠s满足u（s*，s*）=u（s*，s），则必有u（s*，s）>u（s，s）。复制动态是描述在一个种群中，采用某一特定策略的频数的动态微分的方程。若一种策略的收益比种群的平均收益高，其在种群中延续。微分方程表达式：1/xn*dxn/dt=[u（n，s）-u（s，s）]，n=1，2，3，…，N（n为不同的策略;xn为采用策略n的比例;u（n，s）为采用策略n的支付期望;u（s，s）为平均支付期望）

（二）模型的假设与构建

1、博弈模型假设

假设1：在博弈模型中，博弈主体是中国和美国。在经济模型中，双方的地理位置、政治经济体制、文化差异以及政治诉求不同，最开始不能达到纳什均衡的最优博弈结果。中美双方在博弈过程中，相应改变己方的博弈策略以求利益最大化。

假设2：博弈模型中，中美双方可采取的策略集合：（合作，竞争）。

假设3：中方选择继续合作策略的概率为p，则中方选择竞争的策略概率为1-p，p∈[0，1];美方政府采取继续合作策略的概率为q，则美方选择竞争的策略概率1-q，q∈[0，1]。

假设4：中美双方持续打贸易战，所获收益分别为A1、A2;中美双方结束贸易战选择继续合作策略，所获收益分别为B1、B2表示，中美双方继续合作收益B=B1+B2。

假设5：中美双方继续选择经贸继续合作需投入前期成本，包括时间成本、谈判成本和交易成本。中美双方的投入成本分别为C1、C2。

假设6：中美一方选择继续合作，另一发选择竞争，则选择合作一方会遭受损失为L1、L2;竞争方获得收益为M1、M2。

2、博弈模型构建

根据上述六假设，可得中美双方在贸易中的博弈矩阵图5

中方选择继续合作策略：E中1=q（A1+B1-C1）+（1-q）（A1-C1-L1）;中方选择竞争策略时收益期望E中2=q（A1+M1）+（1-q）A1;中方期望收益E中=pE中1+（1-p）E中2

美方选择继续合作策略：E美1=p（A2+B2-C2）+（1-p）（A2-C2-L2）;当美方选择竞争策略收益期望E美2=p（A2+M2）+（1-p）A2;美方平均收益E美=qE美1+（1-q）E美2

3、复制动态方程

由构建模型，得中方复制动态方程：f（p）=dp/dt=p（E中1-E中）=p（1-p）[q（B1+L1-M1） -C1-L1]

同理，得美方复制动态方程：F（q）=dq/dt=q（E美1-E美）=q（1-q）[p（B2+L2-M2）-C2-L2]

联立上述二式得到5个博弈均衡点：N1（0，0）、N2（0，1）、N3（1，0）、N4（1，1）、N5（C2+L2/B2+L2-M2，C1+L1/B1+L1-M1）

4、雅可比矩阵与均衡点稳定性分析

由复制动态方程，对p、q求偏导，得雅可比矩阵

J=（df（p）/dp，df（p）/dq）=（（1-2p）[q（B1+L1-M1）-C1-L1]，p（1-p）（B1+L1-M1））

df（q）/dp，df（q）/dqq（1-q）（B2+L2-M2），（1-2q）[p（B2+L2-M2）-C2-L2]

当B1-C1>M1，B2-C2>M2，中美双方选择继续合作的收益大于中美一方选择竞争而另一方选择继续合作获得的收益，N5（C2+L2/B2+L2-M2，C1+L1/B1+L1-M1）此时在坐标系Y=1，X=1在的第一象限围成的面积内移动。

将5个博弈均衡点：N1（0，0）、N2（0，1）、N3（1，0）、N4（1，1）、N5（C2+L2/B2+L2-M2，C1+L1/B1+L1-M1）代入雅可比矩阵行列式和迹，得：

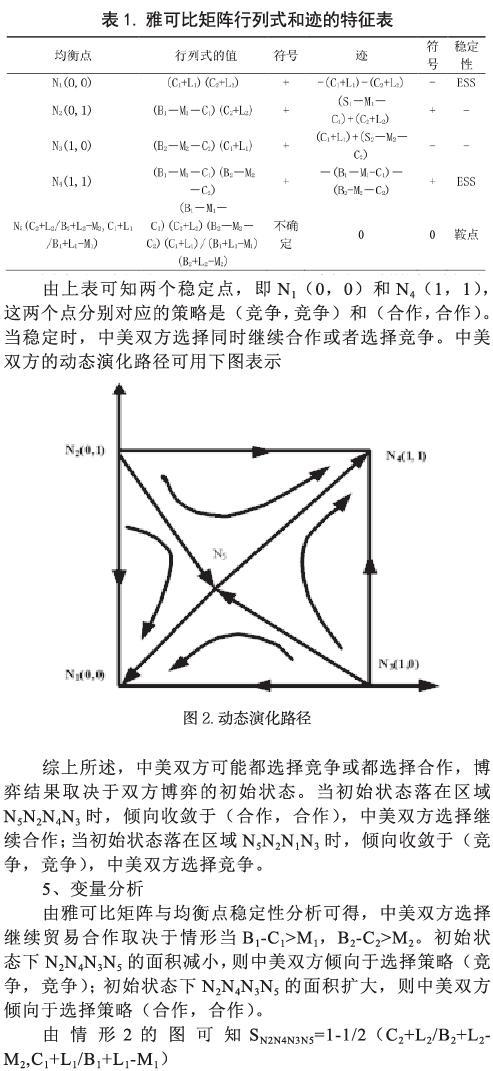
由上表可知两个稳定点，即N1（0，0）和N4（1，1），這两个点分别对应的策略是（竞争，竞争）和（合作，合作）。当稳定时，中美双方选择同时继续合作或者选择竞争。中美双方的动态演化路径可用下图表示

综上所述，中美双方可能都选择竞争或都选择合作，博弈结果取决于双方博弈的初始状态。当初始状态落在区域N5N2N4N3时，倾向收敛于（合作，合作），中美双方选择继续合作;当初始状态落在区域N5N2N1N3时，倾向收敛于（竞争，竞争），中美双方选择竞争。

5、变量分析

由雅可比矩阵与均衡点稳定性分析可得，中美双方选择继续贸易合作取决于情形当B1-C1>M1，B2-C2>M2。初始状态下N2N4N3N5的面积减小，则中美双方倾向于选择策略（竞争，竞争）;初始状态下N2N4N3N5的面积扩大，则中美双方倾向于选择策略（合作，合作）。

由情形2的图可知SN2N4N3N5=1-1/2（C2+L2/B2+L2-M2，C1+L1/B1+L1-M1）

中美双方选择继续贸易合作取决于上式中B1、B2、C1、C2、L1、L2、M1、M2的数值大小，在其他变量不变的情况下，变化其他单一数值，根据计算得出结果：SN2N4N3N5与变量B1、B2数值呈正向关系，与变量C1、C2、L1、L2、M1、M2数值呈反向关系。

合作收益B1、B2与SN2N4N3N5成正比例变化关系，合作成本C1和C2，单独一方选择合作而另一方选择竞争使选择合作一方的损失L1和L2，单独一方选择竞争而另一方选择合作给选择竞争一方的收益M1、M2均与SN2N4N3N5成反比例变化关系。这说明中美双方选择继续合作所能够获得的合作收益越多，中美双方越趋向于选择合作策略;合作成本值越小，单独一方选择竞争而另一方选择合作给选择竞争一方的收益越小，单独一方选择合作而另一方选择竞争使选择合作一方的损失越小中美双方越趋向于选择继续合作策略。

四、结论与政策建议

根据博弈模型，中美双方结束贸易战的关键因素在于双方选择继续合作的收益、成本以及中美任何一方选择继续合作而另一方选择竞争的收益与成本间的差值大小。因此，中美双方结束贸易战应采取可能的方式，增加继续经贸合作收益，减少继续经贸合作的成本，同时减少中美任何一方选择竞争而另一方选择合作的收益。

基于结论给出政策建议

1、中国出口美国贸易总额占中国出口总额比值近几年稳定在20%左右，而美国出口中国贸易总额占美国出口总额比值趋近于10%。相对美国而言，中国更加离不开美国这一贸易合作伙伴。因此中方在贸易上可以适当做出一定的让步，中方可以在技术转让、网路盗窃、知识产权、服务业、汇率、农业及非关税贸易壁垒等领域向美国略微让步，还包括中国增加购买农产品、能源和半导体产品等。

2、从博弈模型可知，中美双方合作收益的提高可以增强经济方合作动力中美双方应开拓贸易合作方式，持续降低继续贸易合作的成本。中美双方应通过谈判，签订贸易协定，修改相关双边投资规则以开拓中美双方有效的贸易合作机制，降低双边贸易成本。

3、中美双方亟待增加贸易摩擦争端解决机制，减少摩擦扩大可能性。作为GDP和贸易量处世界第一第二的贸易国，难免出现经济学中搭便车现象，不可避免出现贸易摩擦。但中美双方可以控制贸易摩擦扩大以避免出现中美任何一方倾向选择竞争，因此双方亟待增加并强化贸易摩擦争端解决机制，减小贸易摩擦扩大化的可能性。

综上所述，尽管中美双方在政治、经济、文化等领域都有竞争博弈，但中美双方贸易总量对世界贸易影响巨大，中美双方应尽快结束贸易摩擦，并建立长久有效的贸易合作机制。

【参考文献】

[1] 博弈与社会[M].北京大学出版社，张维迎，2013.

[2] 产业国际转移视角下的中美贸易摩擦研究[J].蓝庆新.国际经济合作.2007.

[3] 经济相互依赖与中美贸易摩擦：基于多阶段博弈模型的研究[J].邝艳湘.国际贸易问题.2010.

[4] 基于重复博弈模型的中美贸易战探讨[J].孙梦男，魏德来，吴迪.中国市场.2018.