越江联络通道原位冻结试验温度场规律分析

蔡益平，陈军浩，李栋伟3，丁国胜4，姚志雄

(1. 地下工程福建省高校重点实验室，福建 福州 350118；2. 福建工程学院 土木工程学院，福建 福州 350118；3. 东华理工大学 土木与建筑工程学院，江西 南昌 330013；4. 福州地铁集团有限公司，福建 福州 350009)

冻结法因其具有止水性、较高冻土强度和对复杂地层适应性等特点，已成为地铁联络通道的主要施工方法[1-3]。

国内外学者对冻结温度场做了大量的研究和模型试验，获得了有关冻结温度场的发展规律。孙雪兵[4]研究了江底沙土采用冻结法加固的安全可靠性并提出减小集水池体量的方案；丁航等[5]通过数值模拟比较静水、动水条件下冻结壁发育差异，对降低地下水流速对冻结壁发育的危害提供手段；E. Pimentel 等[6]基于水热耦合方程，通过有限元软件模拟渗流条件下冻结壁变化规律；陈雪莹[7]等对联络通道的加固进行了比选分析，最终得到在注浆加固的基础上再进行冻结加固的安全可靠性；M. Vitel 等[8-9]通过渗流条件下三维冻结实验，为与多孔介质相变相关的水热耦合研究提供了关键参数依据；许黎明等[10]研究了海底联络通道健康监测技术，提出安全可行的监测指标与方法，保证冻结施工的有序进行。

以上都是针对低流速、低渗透地层中单排、两排冻结壁发展规律，而对高渗透地层中冻结壁形成规律的试验，尤其是原位冻结试验研究，国内外鲜有报道。本文结合实际工程，利用现场盐水冻结系统开展1∶1比例原位冻结试验，依据单孔、双孔、三孔冻结原位试验，对高渗透地层中冻结壁形成的极限厚度、向外扩展速率及冻结平均温度进行了试验分析得到丰富数据，以求对高渗透地层的冻结壁发展规律进一步了解。

1 工程概况

福州市轨道交通2号线某区间，联络通道的覆土深度约17.3 m，位于江底下方，江底以砂土为主，局部零星分布淤泥，联络通道中心与江底最大垂直距离约20.5 m，与江水近年最高潮位垂直距离约31.4 m，围岩等级为VI级。联络通道所处地层主要为粗中砂、卵石，渗透系数分别达到45、55 m/d，均为强透水地层。通过实际测试地下水流速最大值达到2.46 m/d。联络通道开挖断面大小约为4 400 mm(宽)×5 100 mm(高)；联络通道开挖长度约为7.6 m。

2 原位冻结试验方案

2.1 原位冻结试验设计

为更好地了解高渗透地层联络通道的温度场发展规律、掌握单排冻结模式和双排冻结模式的冻结影响，利用现场盐水冻结系统在联络通道开挖反方向钢管片位置，开展1∶1比例高渗透地层单孔、双孔、三孔原位冻结试验。其中，双孔冻结是为了模拟单排冻结模式，三孔冻结可以模拟冻结现场拱顶双排孔冻结模式。为了保证冻结施工方便，冻结孔与测温孔均按水平角度布置，其中开设冻结孔6个(编号D1～D6)，间距800 mm。其中设计的最低盐水温度为-28～-30 ℃，单孔盐水流量5～8 m3/h，冻结管规格φ89 mm×8 mm。原位试验冻结设计位置及1-1剖面图如图1、2所示。

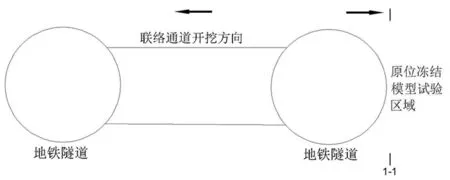
图1 原位冻结试验设计位置图Fig.1 Design position diagram of in situ freezing test

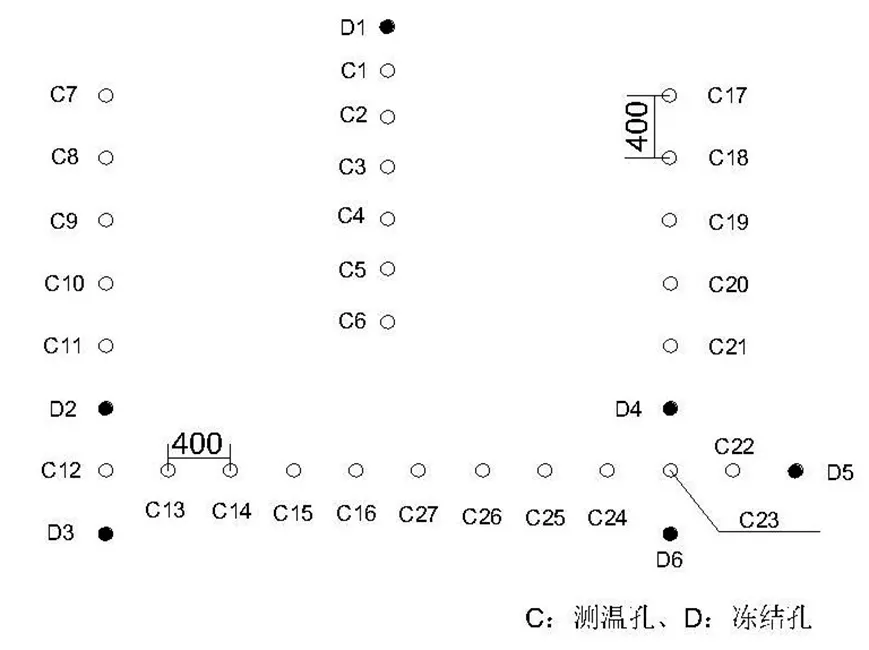
图2 1-1剖面图(单位：mm)Fig.2 1-1 section (unit: mm)

2.2 试验过程监测方案

为把握积极冻结期原位冻结试验的冻结效果，需实时监测整个试验过程。在冻结管与土体进行热交换期间，通过热传感器对地层温度进行实时监测。在测温孔内纵向0.5、1.5、2.5 m处分别设置一个热传感器来测定不同深度土层的实时温度变化情况，其中C1，C2，…，C27 为测温孔编号，共81个测点，测温孔间距为400 mm。由于测试数据较多，本实验采用智能监测技术，设定每隔4 h自动采集数据一次，在冻结帷幕形成过程中实时监测不同位置冻土的温度变化。

3 现场测试结果分析

3.1 原位试验温度实测结果

为将监测数据受外界因素影响降到最低，选取测温孔内纵向三个测点位置的中间测点即1.5 m处的温度数据进行分析。绘制不同冻结模式下C1～C6、C11～C16、C22～C27测温孔1.5 m测深位置土体温度变化曲线，以便更好反映测温孔土体温度随时间的变化情况。图3为不同冻结模式测温孔降温曲线，其中θ表示温度，t表示时间。

图3 不同冻结模式测温孔降温曲线Fig.3 Cooling curves of temperature measuring holes in different freezing modes

单孔冻结在距离冻结管400 mm处的C1测温孔冻结10 d温度下降速率达到1.5 ℃/d，且冻结28 d，C1测温孔的土体温度降到 0 ℃以下，此后曲线变缓，温度下降速率仅为0.11 ℃/d，这是由于测温点处土体的液态水发生相变，进行剧烈的热交换。C2～C6测温孔在冻结10 d温度下降速率均在1 ℃/d以下，且土体温度在冻结过程中均处于正温状态，这表明C2～C6测温孔的位置超出了冻结所能影响的极限半径。双孔冻结模式下冻结初期，C12测温孔附近冻结土温度呈直线下降，冻结10 d温度下降速率达到2.74 ℃/d，而C11测温孔温度下降速率为1.87 ℃/d，这是由于C12受双冷源的影响，温度下降得更低也更快。在冻结过程中随着土体温度逐渐降低，土体内未冻结水含量越来越少，在冻结10 d后土体温度下降梯度变小，随着冻结区域自由水的减少，在冻结30天后温度曲线趋于平缓。三孔冻结模式下，C23测温孔附近土体温度下降速率达到了2.81 ℃/d，C22测温孔周围土温度下降速率为2.74 ℃/d次之，表明距离多个冷源越近，温度下降的越快。随着土体温度不断降低，在冻结20 d左右温度曲线趋于平稳状态。从图3(c)中可以看出有4个测温孔的温度都达到了0 ℃以下，说明冻结的极限半径相对双孔冻结在增大。

3.2 温度场计算方法

冻结温度场是包含相变、移动边界的复杂问题，分析时假设研究的土体是均匀连续且各向同性的粘弹塑性材料；研究的土体为多孔介质材料，忽略土体气相迁移；土体内部仅有冻结管提供热源，水、土之间的热动态平衡是瞬时发生的，水分迁移满足达西定律，无溶质迁移；忽略未冻水含量的影响[11]。

冻结壁厚度的计算在现阶段的地铁工程中还没有较多的研究，国内大多数工程的冻结壁厚度计算都是运用解析公式或冻结壁交圈时间来进行计算，通过计算得到冻结圆柱半径来获得冻结壁厚度。

1)原位冻结试验中单孔冻结是通过实测获得的相关参数，运用解析公式[12]计算得到冻结圆柱半径。

2)双孔冻结是根据线性内插法，可以获得双孔冻结的冻结壁外侧位置

(1)

式中：x冻结壁外边界(m)，T0土体冻结温度(℃)，Ta、Tb近距离、远距离冷源测点温度(℃)，xa、xb近距离、远距离冷源测点距离(m)。

3)三孔冻结即双排孔冻结的冻结壁是由冻结管形成的冻土圆柱的组合体，有效冻结壁即为完整的、连续的冻结壁范围。运用沈阳[13]的总结归纳计算冻结壁厚度。

3.3 冻结壁厚度计算分析

由冻结壁厚度计算结果，可以绘制不同冻结模式下，冻结壁厚度δ冻结随时间变化曲线如图4所示。

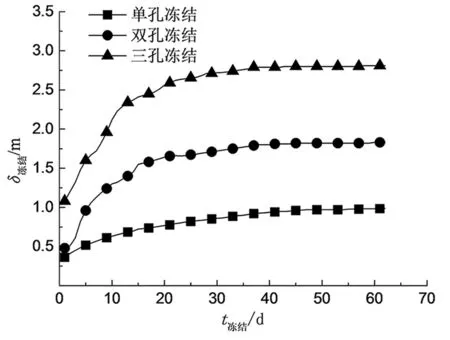
图4 不同冻结模式冻结壁厚度随时间变化曲线Fig.4 Variation curve of frozen wall thickness with time in different freezing modes

通过计算分析获得，在单孔冻结作用下，冻结初期冻结管外侧冻结壁体量相对较小，冻结壁厚度扩展速度也相对较快，冻结15 d时，冻结壁厚度达到0.68 m。但随着冻结持续，冻结壁厚度增长较为缓慢，在冻结30d冻结壁厚度发展至0.85 m，该阶段冻结壁单侧向外扩展速率在5.6 mm/d以内，并随冻结时间推移，冻结壁向外扩展速率逐渐减小。在冻结40、50、60 d冻结壁厚度分别达到0.94、0.96、0.93 m，可见冻结壁极限厚度在0.96 m左右。双孔冻结在冻结孔间距800 mm布置情况下，冻结初期冻结壁向外扩展速率快速增大，后期冻结壁单侧向外扩展速率逐渐减小，冻结15 d时，冻结壁厚度就已达到1.55 m，随着冻结时间的持续，冻结30 d冻结壁厚度达到1.73 m，期间冻结壁单侧向外扩展速率在5.9 mm/d，在冻结40、50、60 d时，冻结壁厚度分别达到1.80、1.83、1.82 m，可见冻结壁极限厚度在1.83 m左右。三孔冻结模式下冻结壁在短时间内即可形成，冻结15 d冻结壁达到了2.41 m，至冻结30 d冻结壁厚度发展至2.71 m，冻结壁单侧向外扩展速率在10 mm/d左右。冻结40、50、60 d冻结壁厚度分别达到2.78、2.80、2.79 m可见三孔冻结的冻结壁的极限厚度在2.80 m左右。

3.4 冻结平均温度计算分析

由冻结平均温度计算结果，可以绘得不同冻结模式下，冻结平均温度θavg随时间变化曲线如图5所示。

图5 冻结平均温度随时间变化曲线Fig.5 Variation curve of average freezing temperature with time

单孔冻结经计算，冻结平均温度最低只有-1.37 ℃不作对比。双孔冻结，冻结10 d冻结平均温度下降速率达到0.4 ℃/d，随后曲线变化较平稳，冻结平均温度稳定在-8 ℃左右。三孔冻结模式下平均温度最低，冻结10 d左右，冻结壁平均温度即可降至-11 ℃左右，冻结平均温度下降速率达到0.5 ℃/d，后期随着冻结壁厚度增大，冻结壁平均温度有略微回升，但稳定在-10 ℃以下。

从以上分析对比单孔冻结、双孔冻结、三孔冻结，在冻结孔间距、排距都为800 mm布置情况下，冻结壁极限厚度达到2.8 m，冻结平均温度稳定在-10 ℃，三孔冻结效果较双孔冻结提升明显。

4 冻结温度场数值模拟

在江底沙土地区，经过冻结后的沙土对温度十分敏感且性质不稳定，应充分考虑其温度大小及冻结时间的影响，正确选用有关设计参数。通过ANSYS有限元软件对软土地层单孔、双孔、三孔温度场进行数值模拟，并通过现场实测和数值模拟的对比，进一步探讨冻土温度场变化规律。

4.1 冻结温度场数学方程

根据多孔介质传热理论和热量守恒定律[14]，若不考虑土体的内热源, 轴对称条件下冻结温度场控制微分方程[15]为

(2)

正冻土中水分迁移满足水流的连续条件和达西定律, 即

(3)

式中：T为土体温度(℃)，t为时间(s)，k为介质导热系数[kJ/(m·s·℃)]，r为平面内任意一点距离冻结管圆心距离(m)，vx,vy,vz分别表示x,y,z三个方向的水流速度(m/h)，kx,ky,kz分别表示x,y,z方向的导水系数单[m2/ (h·℃)]，H为水头高度或压力水头高度(m)，α为水分扩散系数。

若3个方向的渗流速度相同 , 则水分迁移方程用极坐标表示为

(4)

式 (2) (3) 为温度场和水分迁移耦合数学模型。

4.2 冻结温度场数值分析

由水文地质资料可知地层温度在26 ℃左右，开挖土层最大渗流系数达到55 m/d。由于地下水渗流对冻结效果的影响，采用ANSYS有限元软件，建立热流耦合有限元模型，以三孔冻结为例截取一平面作为计算模型，冻结外边界取4倍冻结壁有效厚度，计算模型取边长为12 m的正方形，冻结管采用直径89 mm的圆管，计算采用plane55单元。运用三角网格进行平面划分，并对冻结管周围进行加密处理，其中土的冻结温度取-0.67 ℃，计算天数时间为70 d。

数值计算模型假设：土体材质均匀且各向同性，不考虑盐水与冻结管壁之间的对流换热，其中冻结管壁上的温度等效盐水温度，计算中对施工中产生的温度不予考虑。各土层的热物理参数取值如表1所示。

表1 各土层的热物理参数

5 数值模拟结果分析

5.1 冻结施工分析

通过增加渗流边界条件，得到渗流影响下的温度场计算结果。数值模拟分析得出冻结初期，冻结管与周围土体进行剧烈热交换，导致冻结管周围土体降温较快，冻结30 d，冻结壁厚度达到2.31 m，期间冻结壁沿径向内、外侧分别扩展了0.71、0.62 m左右；冻结40 d，冻结壁厚度达2.57 m，冻结壁厚度增长速度变缓，冻结壁沿径向内、外侧分别扩展了约0.80、0.71 m；冻结中后期，冻结壁厚度基本不发展趋于平稳状态，冻结50 d，冻结壁厚度达2.61 m，冻结壁沿径向内、外侧分别扩展了约0.89、0.71 m。冻结60 d，冻结壁厚度趋于平稳在2.60 m左右，可见数值模拟的冻结壁极限厚度为2.60 m。结果表明，模拟冻结壁总厚度与实测温度计算得冻结壁总厚度基本一致。

通过数值模拟计算得出冻结第30、40、50 d时，有效厚度范围内冻土平均温度分别达到-10.17 ℃、-11.26 ℃、-11.53 ℃，与实测数值分析基本一致。

5.2 实测温度场与模拟温度场比较分析

选取3个主平面上的测温孔数值进行对比分析，其中C21位于D4上方400 mm处，C23位于D4下方400 mm处，C25位于D5左边1 600 mm处。从图6可以看出，数值模拟降温曲线与实测降温曲线基本趋势一致。图中模拟的温度前期下降得较慢，后期C23和C25的现场实测温度有所升高，实测数据较数值模拟数据高1～2 ℃，分析原因这是由于模型计算参数与实际土体的计算参数存在误差和越江隧道地下水的流向和流速不规则等问题，导致热量的流失。综上所述，通过现场实测与数值计算相比较，得到的结论基本一致。

图6 三孔冻结现场实测与数值模拟对比降温曲线Fig.6 Comparison and cooling curves of field measured data and numerical simulations of three-hole freezing field

6 结论

1)三孔冻结在冻结孔间距、排距都为 800 mm布置情况下，冻结15 d冻结壁厚度就达到2.41 m，随后冻结壁厚度增加较缓，至冻结30 d冻结壁厚度发展至2.71 m，期间冻结壁单侧向外扩展速率在10 mm/d左右，此后冻结壁厚度增长不大，至冻结50 d冻结壁厚度仅发展至2.8 m，冻结60 d冻结壁厚度下降0.01 m，可见三孔冻结的冻结壁的极限厚度在2.8 m左右。

2)冻结10 d时，三孔冻结与双孔冻结的冻结壁对应最低平均温度分别为-8.1℃，-11.6 ℃，温差为3.5 ℃，证明三孔冻结即双排管有明显的冻结优势。

3)综合分析，在地下水影响下的高渗透地层中采用双排管或多排管冻结效果好，冻结平均温度更低，冻结壁形成的速率更快。