复数易错题型盘点

蔡海涛

(福建省莆田第二中学 351131)

高考数学中对复数的考查比较基础，一般在选择题或填空题的前几题出现.很多学生见到试题往往认为一看就会,甚至连题目都没看完就迫不及待地贸然下手，结果因为考虑不严谨而在某个环节出现差错．现将复数高考重点考查题型及易错点总结如下，以引起同学们的注意.

一、考查复数的基本概念

例1(2012年高考北京卷·理3)设a,b∈R.“a=0”是“复数a+bi是纯虚数”的

A.充分而不必要条件 B.必要而不充分条件

C.充分必要条件 D.既不充分也不必要条件

错解 C.

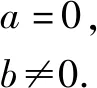
例2(2015年高考上海卷·理15)设z1,z2∈C，则“z1、z2中至少有一个数是虚数”是“z1-z2是虚数”的( ).

A.充分非必要条件 B.必要非充分条件

C.充要条件 D.既非充分又非必要条件

错解认为虚数与虚数的差一定为虚数，选C.

剖析当两个虚数的虚部相等时，它们的差为实数，故不是充分条件，而必要性显然,故选B.

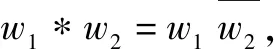
①(z1+z2)*z3=(z1*z3)+(z2*z3)； ②z1*(z2+z3)=(z1*z2)+(z1*z3)；

③(z1*z2)*z3=z1*(z2*z3)； ④z1*z2=z2*z1.则真命题的个数是( ).

A.1 B.2 C.3 D.4

错解对共轭复数的概念及运算性质不清,误选答案.

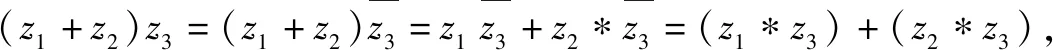
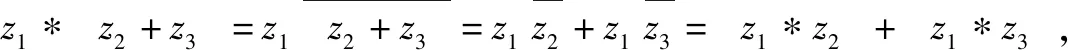
二、考查复数的基本运算

例4(2015年高考江苏卷·3)设复数z满足z2=3+4i(i是虚数单位)，则z的模为____.

错解未能合理应用复数模的性质，先求得复数z导致运算错误.

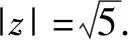
例5(2015年高考湖北卷·理1)i为虚数单位，i607的共轭复数为( ).

A. i B.-i C.1 D.-1

错解混淆了i乘方周期性的性质,导致运算错误.

剖析因为i607=i4×151+3=-i,所以i607的共轭复数为i，选A.

复数中，i是虚数单位,i2=-1；i4n+1=i，i4n+2=-1，i4n+3=-i，i4n=1(n∈Z).

例6(2014年高考上海卷·理11)已知互异的复数a,b满足ab≠0，集合{a,b}={a2,b2},则a+b=____.

错解未理解复数相等的意义,不能正确求解复数方程致误.

剖析(1)若a=a2,b=b2,因为ab≠0且a≠b,无解；

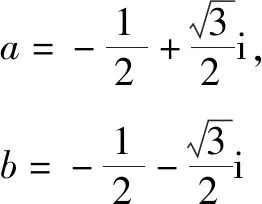
三、考查复数的几何意义

例7 (2016年高考北京卷·理9)设a∈R，若复数(1+i)(a+i)在复平面内对应的点位于实轴上，则a=____.

错解未能理解复数的几何意义,不能对已知复数对应的点位于实轴上这个条件进行合理转化,从而产生错误.

剖析(1+i)(a+i)∈R⟹a=-1，故填：-1.

例8(2014年高考全国卷Ⅱ·理2)设复数z1，z2在复平面内的对应点关于虚轴对称，z1=2+i，则z1z2=____.

A.-5 B.5 C.-4+i D.-4-i

错解未能把两复数对应点关于虚轴对称的几何特征合理转化为两个复数的关系,从而产生错误.

剖析由已知得z2=-2+i,所以z1z2=-5,故选A.

例9(2015年高考陕西卷·理11)设复数z=(x-1)+yi(x,y∈R),若|z|≤1，则y≥x的概率为( ).

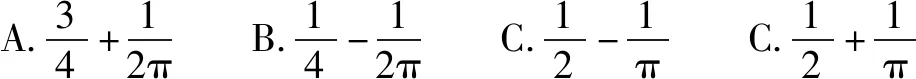
错解不能根据复数的几何意义得到动点(x,y)的轨迹图形，从而致错.

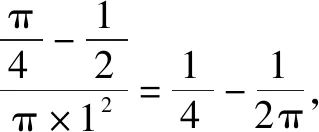
总之，高考中对复数考查比较简单，主要考查复数的基本概念、基本运算、复数的几何意义等．只要我们在解题时多注意辨析概念、细心运算、灵活处理几何意义，复数问题就会迎刃而解．