审视结构特征 构造合理函数——例谈利用导数证明不等式的构造法

范习昱

(江苏省镇江市丹徒高级中学 212143)

利用导数研究函数的单调性极值和最值，再由单调性来证明不等式是函数、导数、不等式综合中的一个难点，也是近几年高考的热点．解题思路是构造辅助函数，把不等式的证明转化为利用导数研究函数的单调性或求最值，从而证明不等式.而如何根据不等式的结构特征构造出一个可导函数是用导数证明不等式的关键，也是难点之处．

利用导数证明不等式的基本的思维程序：根据不等式的特点，构造辅助函数，用导数求出该函数的最值，由辅助函数取最大(或最小)值时不等式都成立，可得目标不等式恒成立，从而把证明不等式问题转化为函数求最值问题.

而利用导数证明不等式的关键在于构造函数，下面选取经典的案例(一些是高考题)，探讨构造辅助函数的几类有效策略.

一、直接移项构造函数

点评当要证的不等式结构比较简单，由基本的表达式(基本的多项式、根式、三角式，对数式等)构成，可以直接移项就能构造函数，这应该是利用导数证明不等式的最为常见和基本的方法．

二、合理换元构造函数

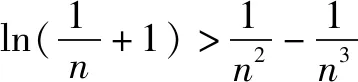
构造辅助函数f(x)=1-x+lnx，证明其最大值小于或等于零即可．

另解构造辅助函数：

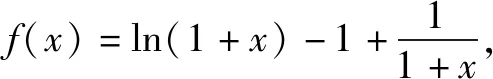
∴当-10时，f′(x)>0，即f(x)在x∈(0,+)上为增函数.因此在x=0时,f(x)取得极小值f(0)，而且是最小值.

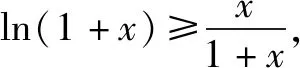
点评一些不等式结构看似复杂，直接移项构造函数，虽然也能证明，但会带来较大的运算量，这样构造的函数并不合理，适当变换后合理换元，再来审视要证的不等式，构造方法便豁然开朗了．

三、恒等变换构造函数

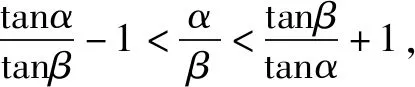
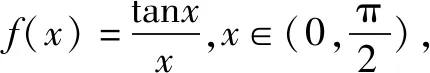
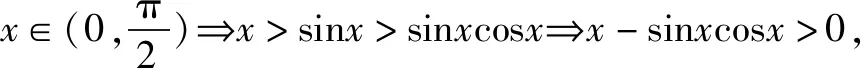
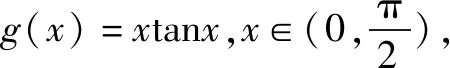
点评一些不等式结构具有双变量的特点，经过恒等变换，能够化成一个函数的两个函数值的关系，根据这种通式便可找到合理的“辅助函数”加以解决．

四、对数变换构造函数

案例5当b>a>e时，证明ab>ba.

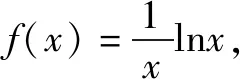
案例6已知m、n都是正整数，且1(1+n)m．

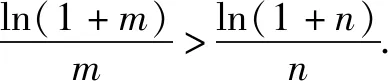
点评一些不等式结构具有幂指数形式，对所证不等式两边取对数，进行恒等变形，就可找到很合理的“辅助函数”．

五、确定主元构造函数

点评这是2004年全国卷理工科第22题第二问，大部分的学生都会望而生畏而放弃，学生的思维盲点主要就在对所给函数不知怎么用，虽然有两个变量，但我们仍然难以像案例3一样通过整体换元，或者像案例4那样通过恒等变换构造辅助函数，但是如果确定一个主元，利用极值偏移的思想，还是能找到合理的辅助函数求解的．

毫无疑问，构造辅助函数是异常艰难的过程，很多学生都会觉得辅助函数是“可望而不可及”的，带着很强的猜测性，其实，我们如能总结这些构造的常见方法，也是能找到很多共性的．当然，还有很多不太常见的构造方法，这里不在赘述．