浅析辅助线在高中数学几何题中的重要作用
邹文韬
(湖南师大二附中 410000)
最为一名高中生在学习数学几何过程中经常会出现无从下手的现象,因此在解题时我们需要对其中的已知条件进行详细阅读,避免陷入出题者设计的陷阱.而在高中几何解题过程中使用辅助线具有重要帮助,有效降低几何题的难度,缩短解题时间,同时还可以提高解题的准确性.
一、高中数学几何学习的难点
高中数学几何题具有难度相对较大的特点,其中还会涉及到计算和证明内容,并且出题者一般会将其他数学知识与几何知识相结合提高题目的难度.我们在解答几何题时感觉比较困难主要表现为以下几点:首先,空间立体思维相对较差,在高中几何解题中需要我们具有超强的逻辑思维能力,但几何题经常会给人一种抽象的感觉,很难在头脑中形成立体画面;其次,在解题过程中很难找到正确的解题思路,看到问题后经常会表现得无所适从,不知该用哪种方式证明;第三,解题方案相对较少,我们在解题过程中经常会出现逻辑思维混乱现象,无法做到举一反三,而且在添加辅助线时也不知道该在什么地方加;最后,对问题分析不足,在解题时对问题的分析不足,从而无法掌握解题条件,因此在解题中经常会出现绘制辅助线错误现象,从而影响解题效果.
二、辅助线在高中数学几何解题中的重要性
1.能够将复杂的几何题简单化
辅助线在解决高中几何问题中比较常见,出题者在出题的过程中经常会将问题复杂化,从而增加问题的复杂难度,因此我们经常会利用辅助线,将复杂的问题进一步简单化,从而便于理解题目.在解题过程中我们需要合理地应用辅助线,让思路变得更加清晰,有效降低几何问题的难度.
例1在三棱柱ABC-A1B1C1中,其底部的A1B1C1为等腰三角形,已知底部∠ABC=90°,同时还知道AA1=AC,并且点D为线段CC1的中点,那么二面角B-B1D-A的大小为多少?

解决以上问题,在思索的过程中会感觉非常复杂,那么首先我们需要画出题目中所给出的条件,如图1.与此同时分析所提出的问题,在解题时直观地计算二面角B-B1D-A的大小非常困难,所以需要引入辅助线.添加辅助线时我们找到AB中点和A1B1的中点引入辅助线EF和CF,紧接着我们还需要作出CC1和EF中点的连线,也就是DG,并连接AB1和DB1,具体辅助线如图1.因此在解题中采用垂面,作出其中的垂线进行解题,并画出其中的点H,以此来确定其中的二面角,最后再对问题进行分析就会显得比较简单.
2.能够体现出隐含的已知条件
在高中几何解题中经常会出现隐含条件现象,从而增加解题难度,因此在平时练习几何解题时,需要对已知条件进行全面了解和分析,充分挖掘其中的隐藏条件,并适当添加辅助线,降低几何题目的难度.
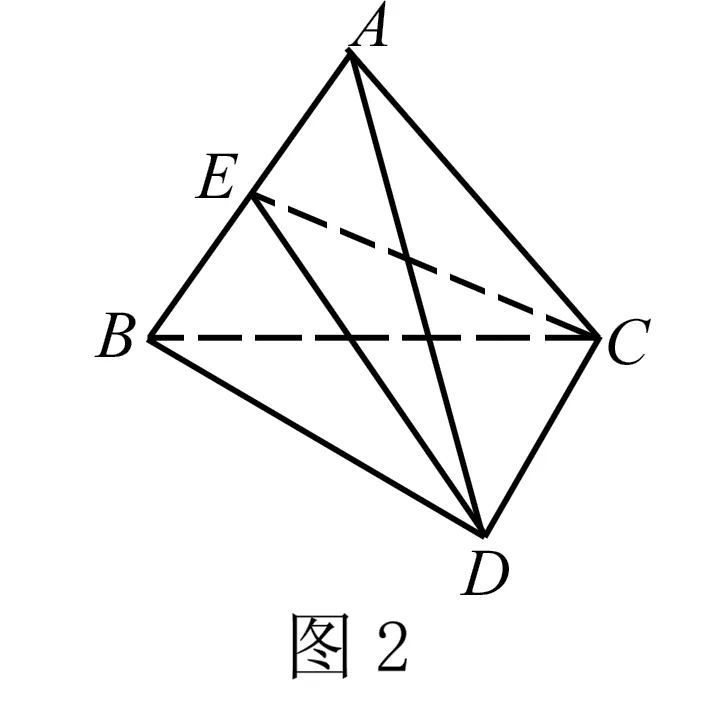
例2 已知空间四边形ABCD,其中的AD与BD相等,AC与BC相等,并且点E为AB的中点.证明平面CED与直线AB垂直.
在解题过程中,先画出问题中已知的条件,从而呈现出题目中所给出的条件,让整个解题思路变得更加清晰(如图2).在证明以上问题中所提到的平面CED与直线AB相垂直过程中,需要合理应用等腰三角形三线合一的性质,因此在解题时首先应该求证直线AB同时垂直于DE和EC,然后再证明一条直线垂直于两条相交的直线,那么该直线就垂直于这两条直线共同所在的平面,最后得出平面CED与直线AB相垂直.根据对以上案例进行分析,可以得出在几何解题中充分应用辅助线对解题有重要帮助,不但能够将抽象的空间问题变得更加直观化,同时对缩短解题时间有重要帮助.
3.将原图形进行变化
在解题过程中将原图形进行平移、旋转等从而得到所需的图形,显露出各线段以及角度之间的关系.

例3已知四边形ABCD,其中AB与CD相等,并且其中点E、F分别为BC和AD的中点,其中BA、EF和CD分别相交,最终形成∠α和∠β,如图3所示.求证∠α=∠β.
在此过程中我们需要引入辅助线,并将其中部分图形进行平移,把∠α和∠β的顶点集中到一个已知点上,同时还需要将直线AB与CD进行平移,因此可以作出以下辅助线,过点F作出FG平行并且等于AB,作FH平行且等于CD,然后将EG、EH、BG以及HC相连接.为了证明∠α=∠β,只需要证明∠1=∠2即可.由于条件可知AB与FG、BG与AF以及FH与DC平行且相等,从而得出△FHG为等腰三角形,并且因为FE是△FGH底边的中线,因此可以推出FE为∠GFH的平分线,因此可得∠1=∠2,由此可得∠α=∠β.
综上所述,高中数学几何题具有空间感强、逻辑思维强的特点,我们在学习和解题过程中不仅难度相对较大,同时解题的准确率也相对较低.经过对上文分析可得,在高中几何解题中适当添加辅助线可将复杂的问题简单化,从而便于我们在解题时能够清楚地了解其中的已知条件,因此辅助线在高中数学几何解题中的重要作用研究,能够有效提高我们的解题质量.

