侧铣加工刀位轨迹优化算法研究*

刘红军，李 斌

(沈阳航空航天大学 a.机电工程学院; b.研究生院，沈阳 110136)

0 引言

非可展直纹面是十分常见的一种曲面，在工程实践中被广泛的应用到航空航天、船舶工业、日常生活等各个领域[1]。这类零件加工精度和零件表面质量对零件的使用性能起到决定性作用，本身具有几何形状复杂，叶片类零件截面薄，加工时容易变形，间隙小加工难度大等问题[2]。因此在数控加工领域对非可展直纹面整体叶轮高质量、高效率数控加工，一直是数控加工领域研究的热点课题[3]。

为了进一步改善加工误差，提高零件的加工精度，近几年，国内外众多学者对侧铣加工非可展直纹面的方法进行了深入的研究，但是主要存在刀轴矢量的计算方法过于传统，缺乏创新[4]。由于非可展直纹面上不同位置的准线并不平行，因此直母线上不同点的法矢各不相同，所以在侧铣加工时存在原理性误差[5]。解决这类问题的方法有两种，第一是将刀位规划转化为单刀位下刀具回转曲面与直纹面间误差优化逼近问题。目前已经提出了单点偏置法[6]、双点偏置法[7]、刀具同被加工曲面三点相切的算法等[8]，这些算法有共同的缺点是误差太大。第二就是从整体或局部误差入手，进行优化。这种方法的原理是控制刀具回转曲面族所形成的包络面与设计曲面之间的误差作为控制对象，不受限于单刀位偏差值的影响，已达到优化的结果。近年来应用最广泛的是最小二乘法[9]，这种方法虽然能得到较好的整体的优化结果，但局部优化能力不如密切法优化效果好。

在非可展直纹面类零件实际加工中，目前还没有一种共享的并且非常具有实用价值的解决方案。针对非可展直纹面精加工刀轴矢量的计算问题，本文提出一种定点旋转并寻求最优刀轴矢量组的计算方法，并且应用密切法算法对刀位轨迹进行整体优化，经过理论分析与实验验证，所提出的方法对非可展直纹面类零件加工精度的提高具有显著作用。

1 加工误差几何模型分析

在几何角度上来讲，误差的大小是根据实际加工曲面与设计曲面之间法向误差来度量的，在每个刀位刀具面族形成了实际上的加工曲面，所谓的误差问题就是研究刀具包络面与设计曲面或称为理想曲面之间的无限逼近问题。如图1所示，本文选择圆柱刀进行加工，在理想加工条件下，就是刀具的包络面与设计曲面之间无限接近，即刀轴的轨迹面相对于设计曲面之间偏置了圆柱刀半径的距离。

图1 误差等价替换示意图

根据非可展直纹面几何结构可知，同一直母线两端法线方向不一定相同。所以对于由直母线偏置所确定的每一条刀轴矢量，其刀具半径大于零时，刀具回转曲面与直纹面区域接触，而非线接触。这就产生了刀具对被加工曲面的过切或者欠切，即为原理误差[10]。扭曲度将对直纹面的侧铣加工的误差有影响，一般来说扭曲度越大，产生的误差也相应增大。

图2 刀位信息计算示意图

参考文献[1]，如图2所示，当刀具位于P1点时，对于凸面过切的最大误差为：

而对于凹面加工过切的最大误差为：

式中，R为刀具半径；R2为P2处的圆曲率半径；α为P1、P2处法矢量夹角。

2 侧铣加工刀位优化

在侧铣加工非可展直纹面的时候，首先要得到离散化的刀位点，通过离散刀位点来确定刀轴矢量，刀轴矢量是影响零件加工质量的重要因素。通过研究三点偏置法原理的的基础之上，本文提出一种定点旋转调整并寻求最优刀轴矢量组的新方法，使刀具回转曲面与非可展直纹面接触状态下局部加工误差趋于最小化。最后通过采用密切法算法做进一步优化处理。

2.1 刀轴矢量组的确定

叶片类零件表面的非可展直纹面是由叶根线和叶顶线离散后相对应点的连线作为母线所构成的，如图3所示，由于非可展直纹面偏置所形成的等距面是自由曲面，不能等同于轴迹面。

图3 刀具侧铣加工直纹面叶片

因此，为了描述方便，本文做出如下定义。 见图3，设r1、r2分别为叶顶线和叶根线，r1′、r2′作为它们沿直纹面法矢方向的偏置线，在r1取一点Mn作为其中一个刀位点，Mn′为Mn在r1′上的对应点，Tα为此时对应下的刀轴矢量。n1，n2……n10为直纹面上的垂直法向量。如图4所示。

图4 定点旋转寻优示意图

为了确定刀轴初始位置，并且满足加工误差，提出单刀位误差函数如下：

|PiQi|为刀轴一点到非可展直纹面的距离；r(Pi)为刀轴一点到圆锥面的距离；c表示刀轴位姿；ε为所允许加工的最大误差。

在通过建立目标函数计算确定刀轴位置离直纹面最近的一点，即公式为：

di=min{d1，d2，d3，……dn}

其中，d1，d2，……dn表示刀轴上各点到直纹面之间的最短距离。

图5 刀轴矢量组流程图

2.2 密切法优化算法

由上述算法得到的一组刀轴矢量只是保证在单刀位处的局部最优。接下来还需要利用B样条插值成非可展直纹面优化后才能达到整体误差最小的结果。接下来利用插值成的直纹面作为基面，利用密切法来达到整体优化的目的。

密切法是通过调整刀具的位置与姿态，使加工出的刀具包络面与被加工曲面在加工路径上形成带状密切。如图6所示，S(1)为被加工曲面，S(2)为刀具曲面，C(b)为被加工曲面上的加工路径。在加工过程中，沿加工路径C(b)，应使刀具曲面S(2)与被加工曲面S(1)处相切接触。

图6 密切法加工示意图

首先，建立局部坐标系：

3 加工误差对比分析比较

计算被加工面的几何误差，就要从微观几何角度分析计算刀具包络面与被加工面的位置关系。在侧铣加工中，几何误差定义为被加工表面与刀具包络面之间的距离。如图7所示，P1为被加工表面上的点，过点P1作刀轴面的垂线并与刀具的理想包络面交于一点P2，在刀轴面上的垂足为P3。可将P1与P2之间的距离定义为侧铣加工的几何误差ε：

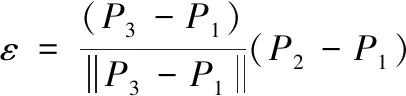
图7 侧铣加工几何误差示意图

从公式可以看出，几何误差ε有正负之分，结果为正时说明侧铣加工时被加工曲面发生欠切，即刀具在切削过程中没有达到预定位置，使多余材料留在了被加工曲面；结果为负时说明侧铣加工时被加工曲面过切，即加工过程中刀具超过预定位置，而过多地切除了一部分材料。

根据文献[10]给出的设计曲面为例，计算圆柱形铣刀加工非可展直纹面加工误差。根据文献给出非可展直纹面设计参数为例，对不同方法的加工误差进行对比，曲面如图8所示，参数如下所示：

r1(u)=[u20.429 0]

r2(u)=[u0.0382u233.995]

S=S(u,v)=(1-v)r1(u)+vr2(u)

u∈[0,23.014]v∈[0,1]

图8 理论设计曲面

加工误差数值计算结果如表1所示。

表1 圆柱刀加工误差对比

由表1和图9直观地反映出两点偏置法出现严重的过切现象，三点偏置法出现严重大面积欠切现象。在本文提出的定点旋转法的基础上应用密切法进一步优化，显著减小了加工误差，加工效果得到明显提高。

(a) 两点偏置法 (b) 三点偏置法 (c) 定点旋转法 图9 误差对比示意图

4 结论

本文对侧铣精加工非可展直纹面进行深入研究，采用单刀位误差度量函数确定初始刀位，通过定点旋转法与密切法得到最优初始刀位。通过仿真结果验证，本文所采用的优化方法所得到的加工误差明显低于现有两点偏置法，修正三点偏置法，提高了非可展直纹面的加工精度，具有很大的经济价值。本文的研究对前人算法的应用进行改进，不在局限于单一传统算法的研究，为传统算法改进开辟新的思路。对非可展直纹面精加工领域提供一定的理论基础。