基于滑移流模型的微型箔片轴承倾斜性能研究
宋国强,伍 林
(上海应用技术大学 机械工程学院,上海 201418)
0 引言
弹性箔片动压气体轴承是一种低功耗、耐高低温、高精密的支承轴承[1]。目前在高速机床、透平压缩机械、燃气轮机等领域得到了非常成功的应用[2-3]。然而随着对机床加工精度、控制精度的提高,当气体轴承间隙尺寸处于亚微米级别时,使用传统无滑移修正的模型对轴承承载估算会有些失实,对此应使用修正后的滑移模型对轴承进行参量特性分析。
Heshmat[4]基于Walowit[5]的波箔片刚度系数公式在不同箔片结构参数下研究了止推箔片轴承性能; lordanoff[6]在一维情况下为气体箔片动压推力轴承实现最佳设计参数创建了一个目标函数计算模型;周权博士[7]运用有限差分法得出了不同结构参数下止推箔片轴承的承载力和扭矩。
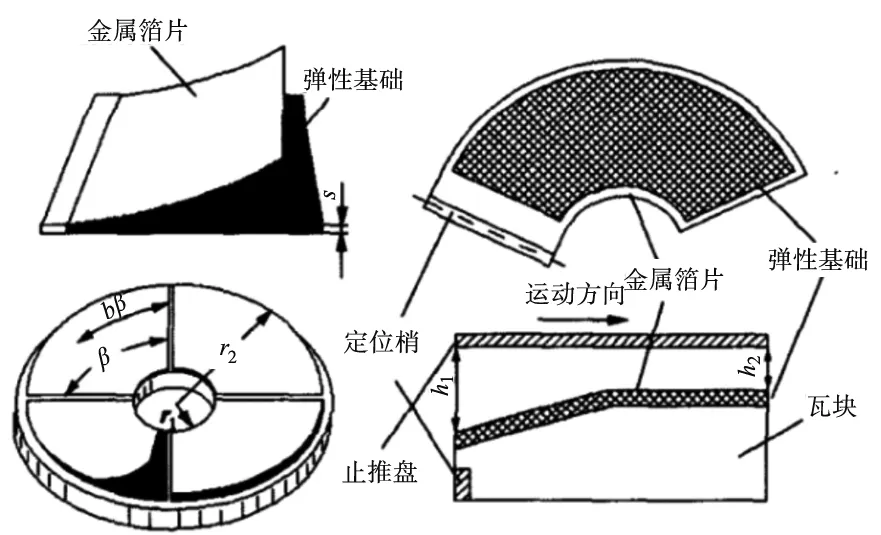
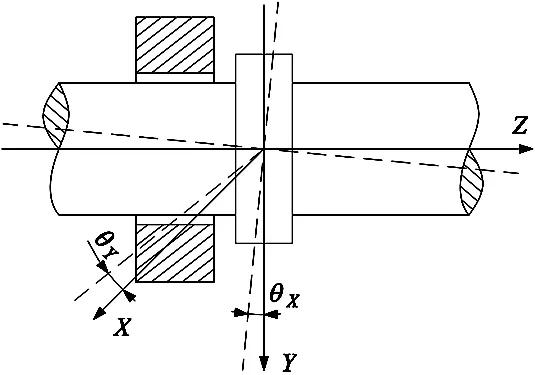
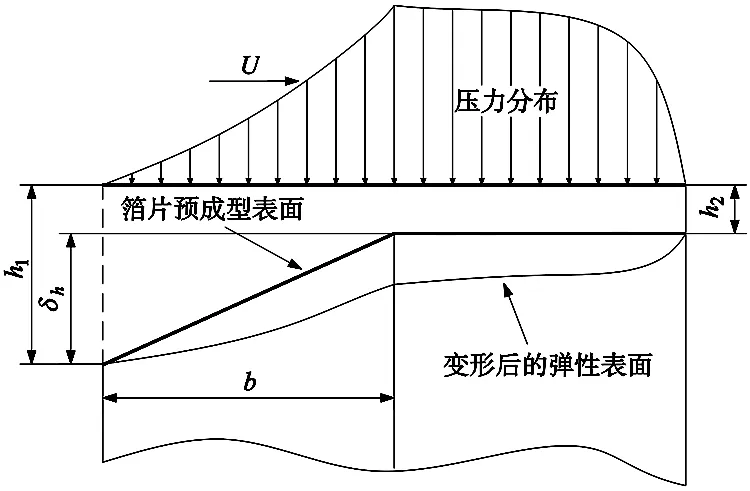
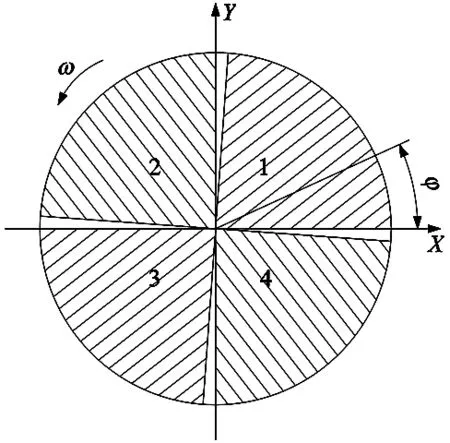
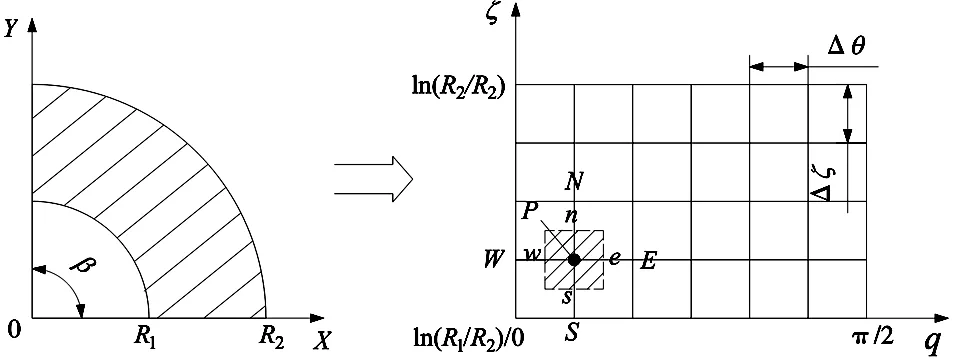
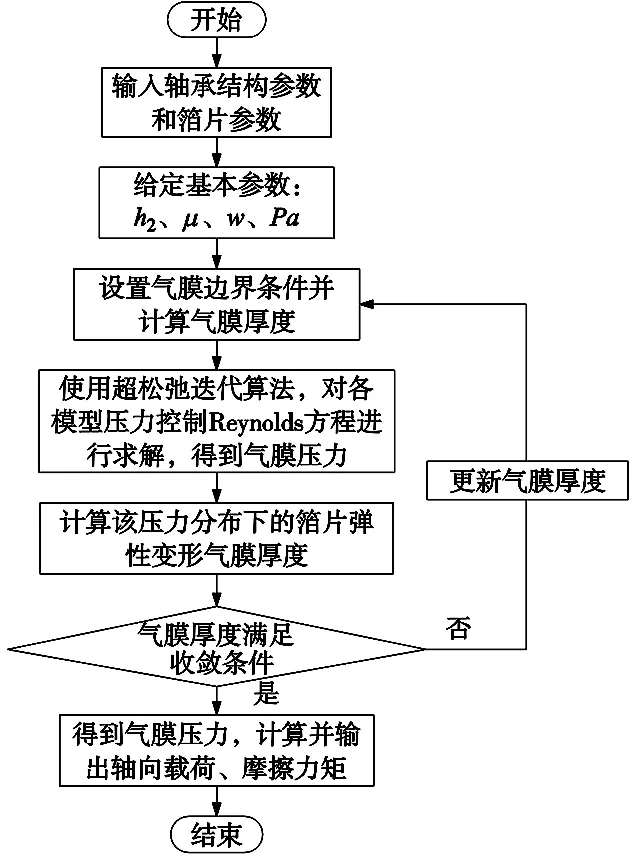
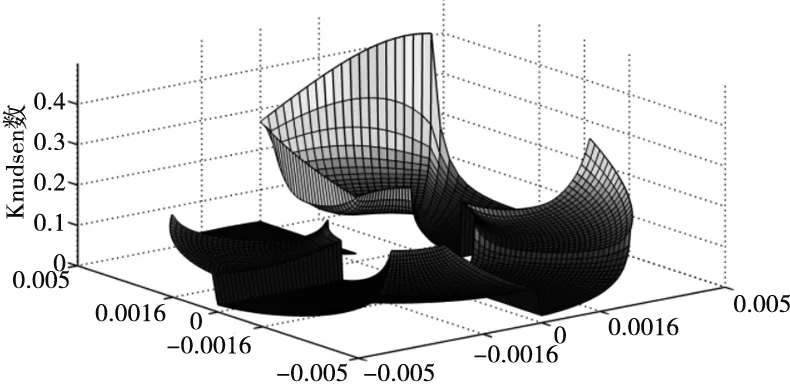
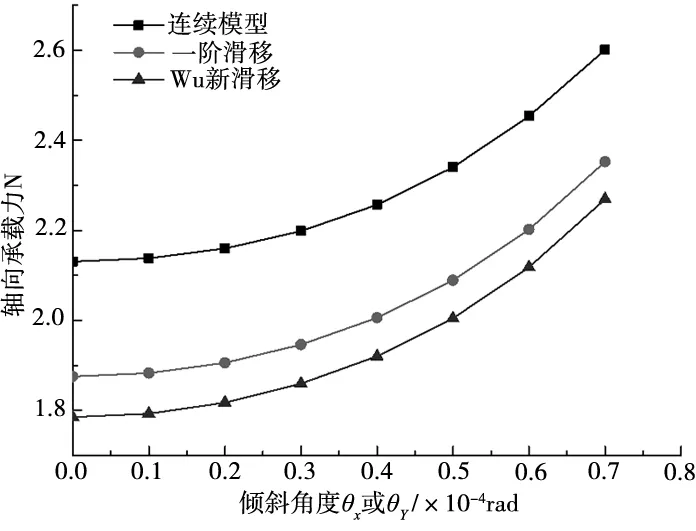
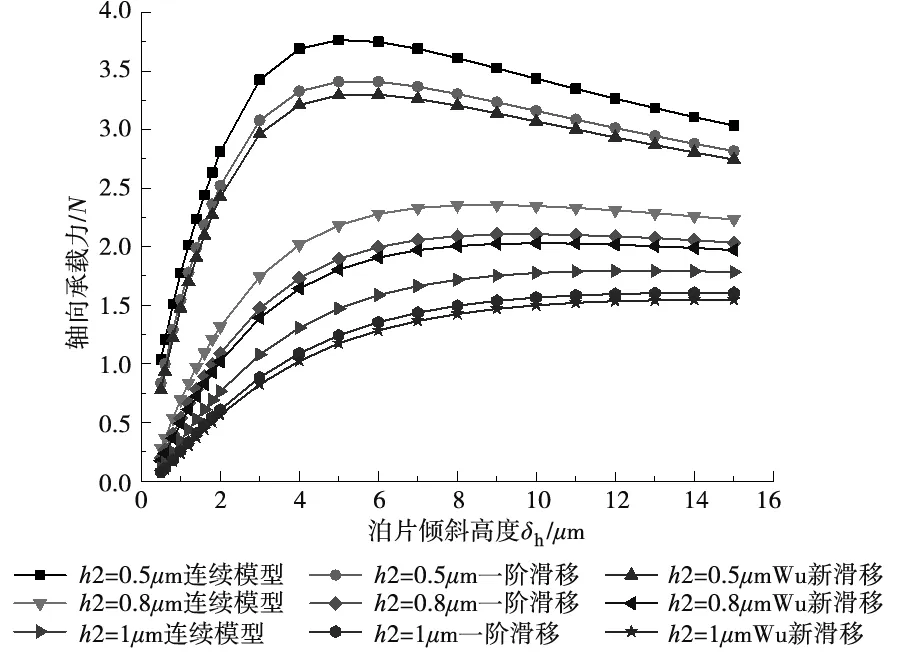
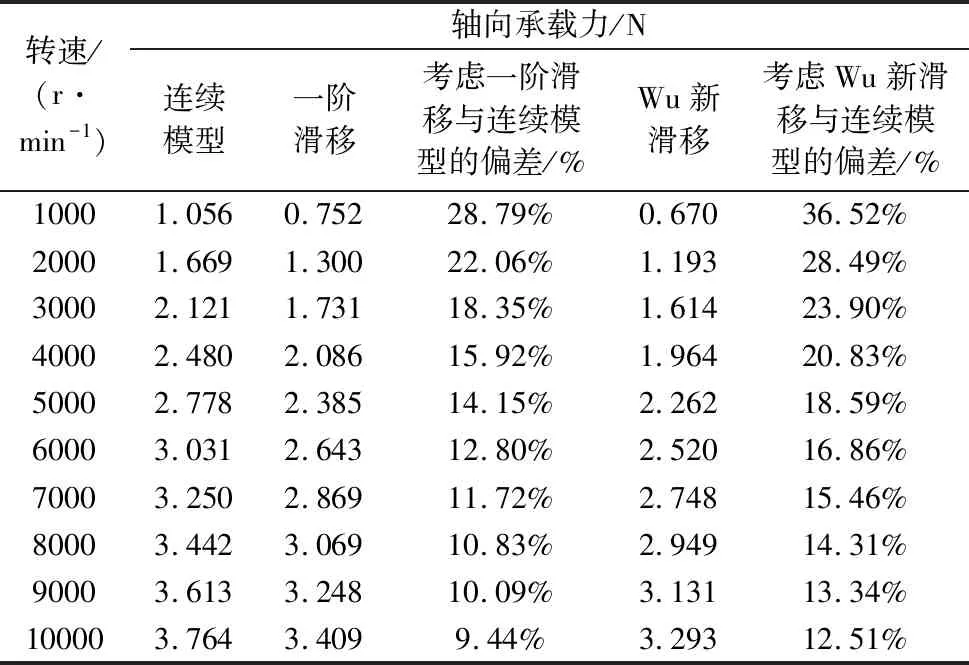
上述研究主要采用传统连续模型来研究止推箔片轴承性能。而对于轴承最小间隙小于1μm倾斜状态下的止推箔片轴承,在整个止推盘倾斜最小气膜间隙到最大气膜间隙过程中,可能会导致其气膜克努森数值由气流滑移区域[8](0.001 本文考虑到轴承转子止推盘倾斜条件下气流滑移效应对轴承承载力的影响,在传统无滑移效应的连续模型主控雷诺方程中引入一阶滑移和Wu新滑移修正项,采用有限体积法求解滑移修正后的各模型雷诺方程,并探讨倾斜条件下,气流滑移效应对不同箔片倾斜高度、不同转速、不同轴承间隙下的止推箔片轴承气膜压力分布和承载力特性的影响。 气体止推箔片轴承一般是由多个有预楔角的扇形轴承座瓦块和弹性箔片元件拼合而成,其结构如图1所示,r1、r2分别为轴承瓦块内、外半径,β为瓦块张角,当轴承转子运转时,气体会因自身的黏性而被带动,并通过楔形空间被压缩,从而获得动压效应支承载荷。这种结构不仅可以冷却吸入的气体,降低箔片和止推盘温度,同时还可增大轴承柔度,避免轴承和止推盘之间发生摩擦。 图1 气体止推轴承结构 在轴承实际运行时,转子往往会出现轴承不对中、弯曲,导致止推盘倾斜,同时改变气膜间隙,气膜压力也发生变化。如图2所示。 图2 转子止推盘倾斜状态 在图2所示坐标系下,X、Y为周向坐标,Z为轴向坐标。假设轴承间的气体黏度不随温度变化,忽略气膜惯性力的影响,引入如下无量纲参数,各参数的物理意义见图3。 (1) 图3 止推箔片轴承结构参数 图3中,h1为扇形箔片进口处与推力盘的间隙,h2为扇形箔片出口处与推力盘的间隙,p为止推箔片轴承间隙气膜压力,h为轴承间隙高度,r为轴承扇形瓦块半径,δh为进、出口处箔片与推力盘间隙高度差,pa为环境气体压力(为101325Pa),R2为箔片扇形瓦外径,u表示弹性箔片的变形量,s为弹性箔片的厚度,k为止推轴承的结构刚度,则传统连续、一阶滑移、及Wu新滑移修正的定常流动雷诺方程为: (2) 不同模型对应不同的系数bs、cs(见表1),f=min[1/Kn0,1]为取值函数。 表1 模型系数 图2中轴承沿X、Y轴倾斜的偏离角用θX、θY表示,因θX、θY过小,可将其近似为: θX≈sinθX,θY≈sinθY (3) 定义无量纲参数为: (4) 则倾斜状态下的无量纲气膜厚度可表示为: (5) (6) (7) 式中,β为扇形瓦张角,b为节距比,即倾斜面部分在扇形瓦块中占的比例,U(R,θ)为弹性箔片在压力作用下的无量纲变形量,α为箔片变形柔度系数,φ为离散网格节点到X轴正向的角度,如图4所示。 图4 直角坐标系中扇形瓦分布情况 弹性箔片止推轴承的气膜压力主控方程是一个非线性偏微分方程。这种方程的解析解难以获得,因此应采用数值方法求解。因为弹性箔片止推轴承结构上的对称性以及各瓦块承载性能相通,所以只需考虑单一瓦块,便能得到轴承的整体性能。令ζ=lnR,求解区域由原来扇形变为矩形网格,如图5所示,Δθ为控制容积周向步长,Δζ为控制容积径向步长,均匀划分求解区域,矩形网格中阴影区域为单个离散点的控制体积单元,则P点的气膜压力控制方程变为: (8) 图5 求解区域变换图 通过有限体积法可将(8)式离散为: APPP=AEPE+AWPW+ANPN+ASPS+SWΔζ-SEΔζ (9) 对式(8)求解过程中,因动压止推轴承运行时,扇形瓦块的每个边界都和环境相通,所以各个边界都为环境边界条件,其无量纲压力边界条件为: (10) 求解过程中先给定气膜压力和气膜厚度的初值,再通过SOR迭代算法求解得到轴承各点的气膜压力和气膜厚度的数值解,程序算法流程图如图6所示。最终得到单个止推箔片轴承的轴向承载力为: (11) (12) 图6 数值求解流程图 为验证本文所用程序的正确性,按表2所示微型气浮箔片止推轴承结构参数,用有限体积法计算,并与文献[7]的仿真结果做对比。 图7给出了本文使用有限体积法计算得到的轴承气膜压力分布图。图8展示了文献[7]中的有限差分法和本文使用有限体积法得到的在R=2处的气膜压力分布图。对比结果表明:两种算法得到气膜压力分布几乎完全一样;使用有限体积法计算得到的无量纲承载力为15.96与文献中的承载力相对误差为1.83%。由此验证了本文算法的准确性。 表2 文献[7]中止推箔片轴承的计算参数 图7 有限体积法算得的气膜压力分布 图8 两种算法得到的在R=2处的气膜压力分布 本文仿真研究所用的微型箔片止推轴承结构参数如表3所示,气膜厚度收敛精度设为10-6。 表3 止推箔片轴承的计算参数 当扇形瓦块张角为90°时,图9~图11分别为在箔片变形柔度系数α为0.060356,转速ω=10kr/min条件下轴承止推盘沿X、Y轴方向各倾斜5×10-5rad角度的Wu新滑移修正模型止推箔片轴承压力分布图、三种模型在周向半径中线处的气膜压力分布图和此状态下的Knudsen数分布图。由图11为可以看出位于倾斜一侧扇形瓦块润滑气膜的Knudsen数远大于气流滑移区域的最大值0.1,气膜厚度与分子自由程处于同一量级,这使得一阶滑移模型已不再适用,需采用任意克努森数下适用的Wu滑移模型来研究轴承参数特性。 图9 设计算例参数下Wu新滑移模型的气膜压力分布 图10 一阶滑移模型无量纲压强 图11 设计算例参数下止推箔片轴承Knudsen数分布图 图12展示了箔片柔度系数α=0.060356,转速ω=10kr/min条件下,转子止推盘在不同倾斜角度时,连续和各滑移修正模型的承载力变化规律。可以看出,随着转子倾斜角度增大,各模型的轴承承载力逐渐增大且有明显差异。这是因为在倾斜角度条件下,转子止推盘有将近1/4区域的气膜Knudsen数大于0.1,局部气膜厚度与气体分子平均自由程属于同一量级,气体分子间的碰撞和分子与壁面的碰撞对气流运动的影响较大且不可忽略,连续模型和一阶滑移修正模型假设对这种情况的考虑不够完善,导致出现模型间较大的偏差。 图12 轴承承载力随倾斜角度的变化情况 图13为基于连续和各滑移修正模型在倾斜角度为5×10-5rad 、箔片变形柔度α=0.060356、转速ω=10kr/min、不同最小气膜间隙条件下,轴承轴向承载力和箔片倾斜高度的关系。从图中可以看出,在箔片倾斜高度增大的过程中,承载力呈现出先增大后减小的趋势,且最小间隙越大,轴承承载力达到最高所需的箔片倾斜高度也越大;随着最小间隙的增大,轴承承载力明显下降,同时承载力的变化越趋平缓,轴承收敛间隙的气膜动压效果明显减弱;各模型间的承载力在一定范围内随着箔片倾斜高度增大有显著偏差; 在轴承最小间隙低于1μm后,Wu新滑移模型计算得到的承载力低于一阶滑移模型和连续模型,各模型间的结果偏差随着轴承间隙的减小也越来越大,印证了文献[9]中克努森数接近0.1时一阶滑移不再适用的结论,需采用对分子碰撞有深入研究的Wu滑移模型来得到更加精确的轴承承载力结果。 图13 轴承承载力随箔片间隙高度的变化情况 表4给出了倾斜角度为5×10-5rad 、箔片变形柔度α=0.060356条件下,三种模型下的轴承轴向承载力和转速之间的关系。随着转速的增加,由箔片收敛间隙结构产生的动压效果增强,轴承承载力也在不断增大。在相同转速条件下,考虑气流滑移效应后,由于滑移速度边界条件的影响,使得轴承间隙的气流压力水平有所降低,导致轴承的轴向承载力降低。在转速较低时,模型结果之间的相对偏差较大,但是随着转速继续增加,各模型间的结果偏差接近一个恒定值。这是因为气流滑移影响是由气膜厚度的Knudsen数决定。随着转速提高,箔片材料变形程度加大,导致气膜间隙增大,相应区域的气膜Knudsen数也降低到一阶滑移模型适用范围,同时基于合理假设的Wu新滑移模型也适用,所以模型偏差降低。这说明箔片柔度系数一定时,高转速下产生的气流滑移效应是有限的。 表4 不同转速下三种模型计算的承载力的对比 针对精密磨削机床中倾斜条件下的微型止推箔片轴承结构,分别采用连续模型、一阶滑移模型和Wu新滑移模型速度边界条件,推导出考虑气流滑移效应的修正雷诺方程。采用有限体积法对其进行求解,得到三个模型在不同倾斜角度、不同箔片倾斜高度、不同轴承间隙高度和不同转速下的轴承承载力结果。对比结果可得出如下结论: 相对于连续模型,利用滑移修正后的模型对倾斜条件下的微型止推箔片轴承承载力计算结果随倾斜角度、箔片倾斜高度、最小气膜间隙的变化有明显改变。当最小气膜间隙、轴承转速和倾斜角度降低时,滑移修正模型得到结果远小于连续模型,且模型间的结果偏差也被放大。通过有限体积法求解滑移修正模型可得到较为精确的微型止推箔片轴承参量特性,以便为相关精密磨削机床的安全运行提供精确数据以及为精密磨削余量的的计算提供坚实的理论基础。1 气体止推箔片轴承结构
2 考虑气流滑移效应的压力控制方程
2.1 止推盘倾斜状态下的修正雷诺方程
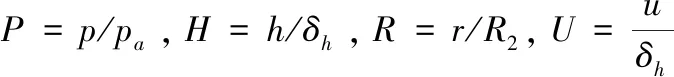
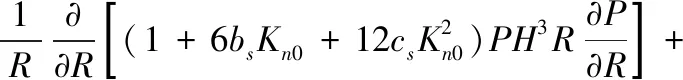
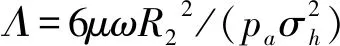

2.2 止推盘倾斜状态下气膜厚度方程
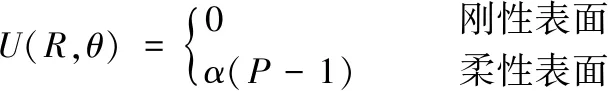
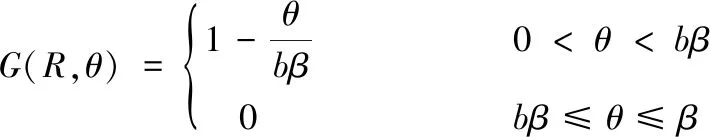
3 控制方程有限体积法数值求解

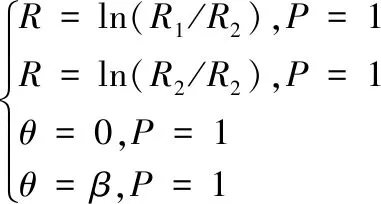
4 仿真结果验证与分析
4.1 程序的验证

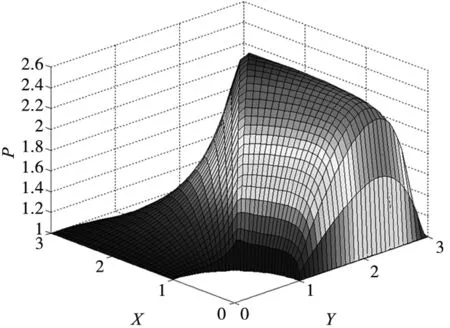
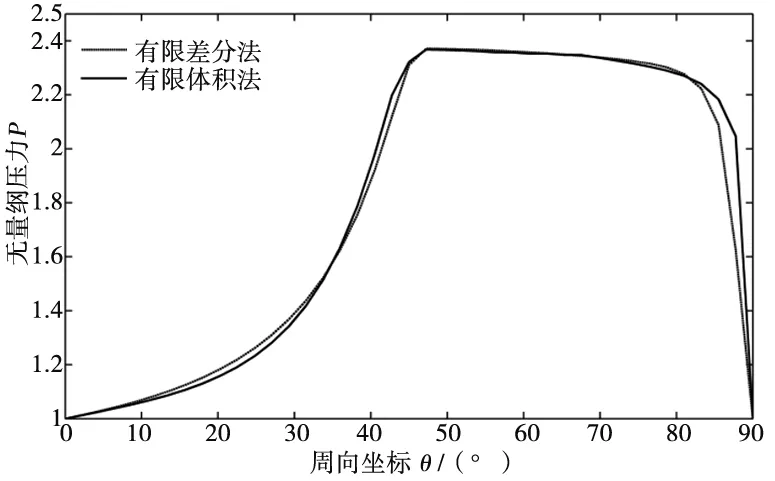
4.2 转子止推盘倾斜条件下的轴向承载力分析

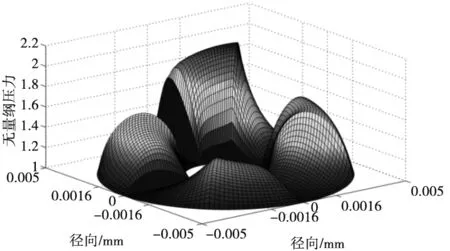
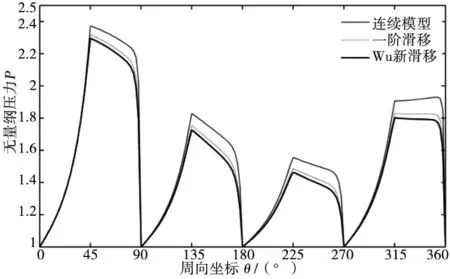
5 结论

