GMDH神经网络在电主轴热位移建模中的应用
万正海,李锻能,潘岳健
(广东工业大学 机电工程学院,广州 510006)
0 引言
机床高速电主轴内置电机发热严重、轴承摩擦发热量大、结构复杂,由热不平衡所造成的热变形在很大程度上直接影响主轴的加工质量。如何减少高速电主轴的热误差是一个亟待解决的问题。
由于热误差受主轴零部件形状结构、装配精度和冷却效果等因素的影响,成为一个复杂的非线性系统,因此准确建立热误差预测模型是热误差补偿实施的关键第一步。采用解析法建立预测精度较高的模型比较困难,而基于人工神经网络的非线性建模技术由于能够逼近任意复杂的非线性系统,自学习和自适应动态的系统,鲁棒性较好而广泛应用在机床热误差预测建模方面[1]。
近些年来,国内外学者针对机床主轴的热误差建模技术做了大量的研究。谭峰等[2]提出一种集成BP神经网络的数控机床主轴热误差建模方法,其模型的预测精度和泛化能力优于单一BP神经网络,但存在模型训练速度慢、较难获得全局最优、对初始权重较敏感的不足。苏铁明等[3]针对卧式数控机床主轴热误差,建立了基于FCM聚类和径向基(RBF)神经网络模型,相比传统的RBF神经网络,降低了变量耦合影响,鲁棒性更强,但其网络模型参数确定较为困难、对样本依赖性大。章晓英[4]提出了基于蚁群算法优化的BP神经网络,通过仿真实验表明其预测效果明显优于BP神经网络以及 PSO-BP神经网络。上述神经网络的预测精度一般会受到训练误差的影响,模型稳定性也会受到网络训练速度的影响,最终会引起模型预测性能的不稳定。
本课题针对之前学者研究的不足,以高速数控机床电主轴为研究对象,利用传感器采集到的电主轴的热误差实验数据,建立基于GMDH(data processing clustering method)神经网络算法[5]的主轴热误差预测模型。在GMDH神经网络建模的过程中,由于模型结构和变量的自动筛选,避免了模型结构的过拟合和不足拟合的问题[6],也减少了主观因素对网络的影响,模型的稳定性有了较大提高,也具有更好的可移植性。
1 电主轴热误差测试实验
为了获得GMDH神经网络的热误差建模的数据,以某型号高速数控机床电主轴为研究对象进行热误差实验。为了避免测量的多个温度变量的耦合,在优化主轴测温点的基础上,选择一个温度探测点测量电主轴实时温度变化。将一只温度传感器贴附在探测点,另外安装一只温度传感器记录环境温度的变化。为了测量主轴轴向热变形,将一个测量芯棒装在刀柄上,同时设计制造一个特殊夹具用于夹装电涡流位移传感器。芯棒的被测量端面经过平面处理,减小位移传感器在非接触测量时由于被测量端面的不平整所引入的位移波动误差。测试过程及传感器的布置如图1所示。

图1 主轴热误差实验测试
在实验之前,为了使得机床处于完全冷却状态并保证所采集数据的准确性,先将机床停机12h以上。一般认为机床空运转状态下的功耗是精密机床的一个主要热源,所以将机床空转下的热特性作为评价机床的一个重要指标。实验机床从停机状态以变转速8000-16000-24000r/min连续运转3h,每个转速运行1h。传感器每隔1min采集一次温度和轴向热位移数据,共测得180组数据。由于主要研究对象为机床温度与主轴轴向热误差的关系,所以需要对测得的数据进行整理。将测得的主轴轴向热位移误差数据减去0时刻对应的热误差。得到了电主轴温度和环境温随时间变化的曲线如图2所示,电主轴轴向热误差随时间变化的曲线如图3所示。
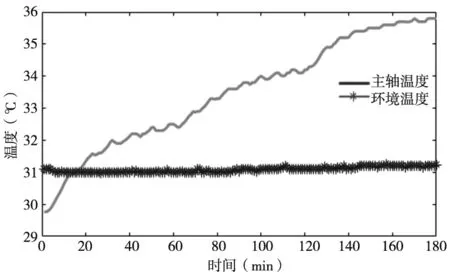
图2 电主轴温升曲线
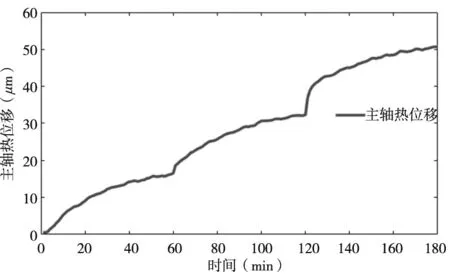
图3 电主轴轴向热误差变化曲线
由图2知,电主轴的温度随着转速增加而升高,最高温度是35.8℃,最大温升为5.8℃,环境温度31℃,且基本维持不变。由于冷却机的启停较为频繁,主轴温升也会产生一定幅度的波动。从图3中可以看出,电主轴轴向热误差变化趋势的与主轴温度变化趋势基本一致,最大轴向热误差量为50.7μm。转速越高,主轴轴向热误差变化越大,在转速变化的瞬间,热误差变化最为明显。
2 GMDH神经网络热误差建模
由于主轴的热误差受多种因素的综合影响,其模型是一个非常复杂的非线性系统,采用解析法建立性能较好的模型难度较大,而常规采用的人工神经网络难以给出实际的物理意义和明确的解析表达式,并且在建模过程中需要根据经验对模型的输入参数和结构作一些假设,需要多次试验才能找到满意模型[7]。相比之下,DMGH网络模型能够得到函数解析表达式、建模自组织控制,而且不需作过多假设,很适用于电主轴的热误差建模。
2.1 GMDH神经网络理论
GMDH神经网络是一种组合的多层算法,在这种算法中,神经元层和网络是由被评估的数据流的大量输入生成的。最初由乌克兰科学家Alexy G Ivakhnenko在1968年提出,其网络拓扑使用逐层修剪的过程来确定,该过程基于预先选择的每个级别的最佳节点的标准。GHDH网络的一个明显特点是其网络结构不是固定的,是在学习过程中不断发生变化。GMDH经过训练之后的网络结构如图4所示[8]。
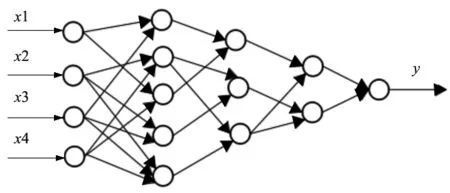
图4 训练后的GMDH典型网络结构
传统的GMDH方法基于一个基本的假设,即数据可以通过使用Volterra级数或Kolmorgorov-Gabor多项式的近似来建模:
(1)
式中,y为系统输出,a0、aj、aij为多项式系数,xi、xj为系统输入变量。
随着多项式(1)级数的增多,其参数确定的计算也会越来越困难。GMDH神经网络是通过层层计算单个神经元模型来逼近多项式(1)。
GMDH神经网络一般是利用自适应线性元件作为神经元,如图5所示。单个神经元输入输出关系可以表示为:
(2)
其中,Zk,1表示第k层的第l个处理单元,Z0,1=x1,wi(i=1,2,3,4,5)为神经元的权值。GMDH神经网络的处理单元最后的输出是2个输入单元的二次多项式,因此网络的每层会使二次多项式的阶数增加2阶,最终网络的输出结果可以表达为输入单元的2k阶多项式,k为GMDH网络层数(不包括输入层)[9]。
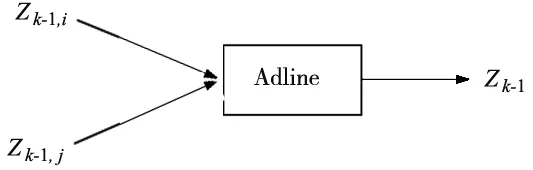
图5 GMDH网络中的神经元
2.2 GMDH神经网络的构建和训练
在构建GMDH网络时,生成所有的输入组合并将其发送到网络的第一层。然后对该层的输出进行分类和选择以输入到下一层,所选输出的所有组合被发送到第二层。只要每个后续层(n+1)产生比层(n)更好的结果,该过程就继续。当发现层(n+1)的结果不如层(n)时,停止该过程[10]。
在训练的过程中GMDH网络的神经元层数一直增加,随之也会添加新的神经元。随着层级进化的过程,性能较差的神经元将会被淘汰,所以每层神经元的数量也是变化的。训练时,优化神经元的权值和网络层数达到设定的精度为止。GMDH神经网络的训练流程图如图6所示。

图6 GMDH神经网络的训练流程
2.3 电主轴热误差模型的建立
将测量的数据导入MATLAB软件建立GMDH神经网络模型,网络模型的输入为归一化后的2只温度传感器采集的数据,输出为位移传感器采集的电主轴轴向热误差数据。采集180组数据,随机选取153组数据(总数据的85%)作为训练样本,剩余的27组(15%)作为预测测试样本。训练过程中取学习率为0.85,最大网络层数设定为4,网络层中最大的神经元个数设置为15。经过训练后的GMDH网络模型的表达式为式(6)所示:
Y=0.0265949-N82×0.390708-N82×N2×0.013967+
N82^2×0.014027+N2×1.38756
(3)
式中,Y是输出量,N82、N2等代表节点单元,通过层层迭代计算得出,如下式所示:
N2=-0.266741-N5×22.8939+N5×N6×2.11367+
N6×23.9202-N6^2×2.11413
N6=-495.016+x1×31.3872+x1×N8×0.0588679-
x1^2×0.496239-N8×0.95971
· · · · ·
· · · · ·
· · · · ·
N338=-170242-x1×13106.7+x1דx1,cubert”×
4132.84-x1^2×64.6525+“x1,cubert”×155997-
“x1,cubert”^2×25721.4
上式中,“x1,cubert”表示x1的立方根。
GMDH网络的预测效果如图7所示,为了比较预测的精度,分别用BP、RBF神经网络训练的预测模型如图8和图9所示。
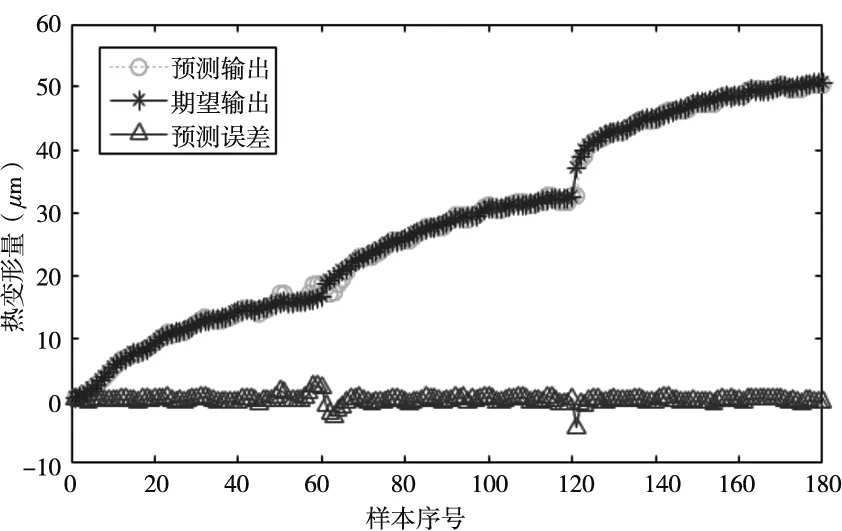
图7 GMDH神经网络模型的预测图
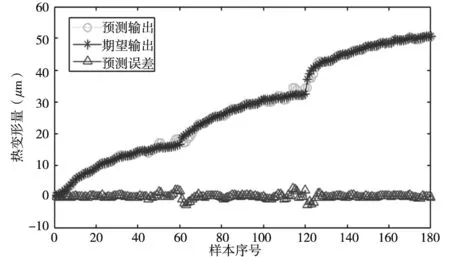
图8 BP神经网络模型的预测图
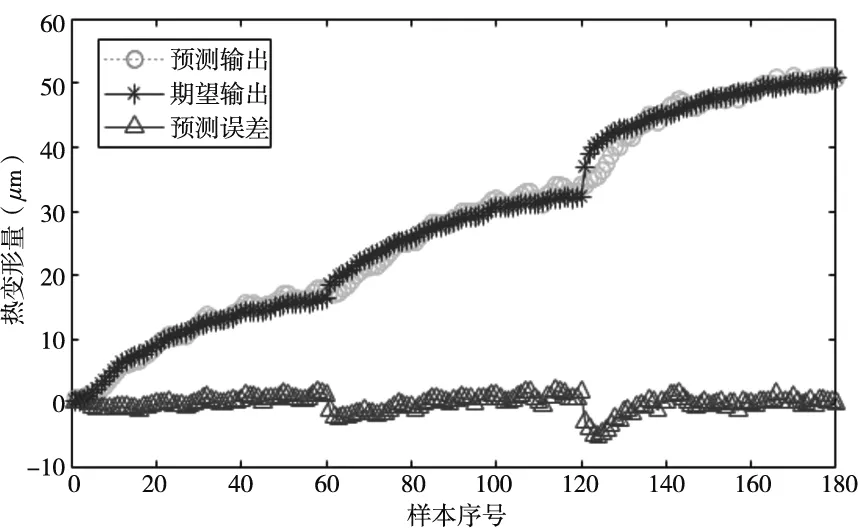
图9 RBF神经网络模型的预测图
将GMDH网络结果与BP、RBF神经网络的结果进行对比分析,采用最大残差、均方差和预测精度作为预测指标,如表1所示。
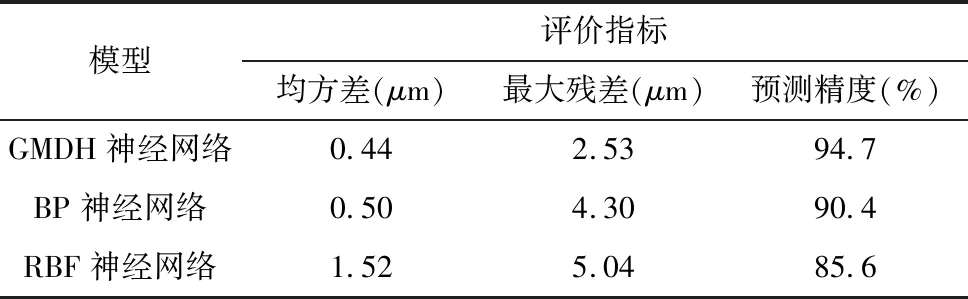
表1 各模型的预测结果对比
从图7~图9可以看出,GMDH、BP和RBF三种神经网络都对主轴轴向热位移误差进行了比较好的预测。在变转速处,三种预测模型都在不同程度与实测热误差曲线出现偏差,但GMDH网络偏差是相对最小的。从表1可以看出,GMDH网络的均方差、最大残差表均为最小,预测精度最高,达到了94.7%。表1的精度指标表明,GMDH神经网络在主轴轴向热误差模型的预测精度、泛化性和稳定性方面都高于传统的BP、RBF神经网络所建立的热误差模型,可以更准确地预测电主轴轴向热误差,从而更好地提高机床的加工精度,适合作为多种复杂工况的机床热误差的预测预测模型。
3 结束语
本文在对高速数控机床电主轴热误差实验测试的基础上,针对传统的神经网络难以给出实际的物理意义和明确的解析表达式的不足,提出了基于GMDH网络的电主轴热误差模型算法,并利用MATLAB平台建立电主轴热误差预测模型。仿真预测结果表明:与传统的BP、RBF神经网络模型对比,GMDH神经网络算法由于模型结构和变量的自动筛选产生,因此具有较高的预测可靠性、更好的泛化性和稳定性。电主轴热位移误差预测建模为机床数控化补偿打下基础。

