推进剂贮箱金属焊接件疲劳裂纹对应力强度因子影响的数值分析

赵 颖，黄 美，杨梦灵，韩 然

（1.华北电力大学 核科学与工程学院，北京 102206； 2.北京卫星环境工程研究所，北京 100094）

0 引言

表面张力贮箱是利用液体推进剂表面张力作用实现在微重力状态下对推进剂进行管理、运输的一种贮箱。其无运动部件，全金属焊接结构，与推进剂相容，有利于发动机在轨长寿命运行[1]，广泛应用于卫星推进系统，可实现卫星变轨、轨道修正、姿态保持等功能[2]。

钛合金是卫星贮箱主体结构的重要选材，其使用对于减小结构质量、提高结构承载效率、满足高温高载及抗腐蚀要求、改善结构可靠性、延长机体寿命等发挥重要作用。超轻型大直径表面张力贮箱是采用超塑成型与真空电子束焊接工艺制造完成的。焊接技术在众多连接工艺中质量效率最高，可提高材料利用率，在卫星上的应用越来越多。于康等[3]对球形表面张力贮箱装配精度与贮箱焊缝熔深及形貌之间的关系进行了研究，建立了电子束焊接工艺规范。由于焊接工艺自身的特点，焊接缺陷必然会对结构的疲劳裂纹产生一定影响[4]。

本文主要通过ANSYS和Simufact Welding软件对表面张力贮箱进行建模及焊接残余应力计算，找到焊接残余应力最高的区域，在该区域引入裂纹，分析裂纹的应力强度因子分布，并通过改变裂纹的插入角度和长短轴之比，对应力强度因子的影响因素进行分析，研究焊接残余应力作用下裂纹的扩展趋势。

1 表面张力贮箱结构简介

贮箱由球形外壳和液体管理装置组成，球形外壳由上、下半球焊接而成，主要材料为TC4钛合金，可供选择的焊接方法有氩弧焊、电阻焊、真空扩散焊等[5]。由于结构设计的需要，贮箱上往往有不同类型的焊缝，需选用不同的焊接方法，对焊接厚度1.5～2 mm以下的环形焊缝，通常采用不加填料的自动钨极氩弧焊[6]。图1为贮箱焊接的简化示意图。图2为使用ICEM有限元网格划分软件对贮箱半球模型进行的网格划分。TC4钛合金的化学成分和力学性能分别见表1和表2。

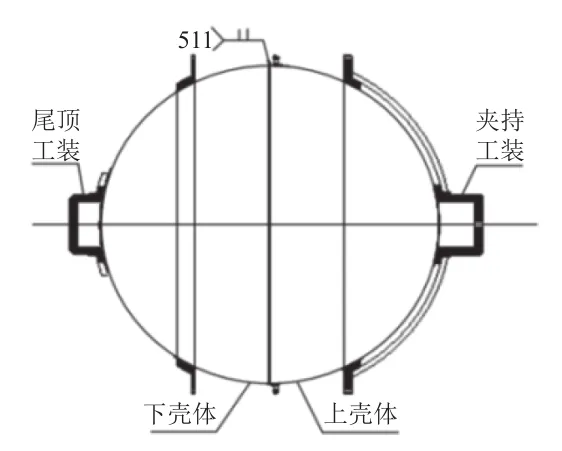
图1 贮箱焊接示意图Fig.1 Sketch of the tank model

图2 贮箱有限元网格模型Fig.2 Finite element model of the tank

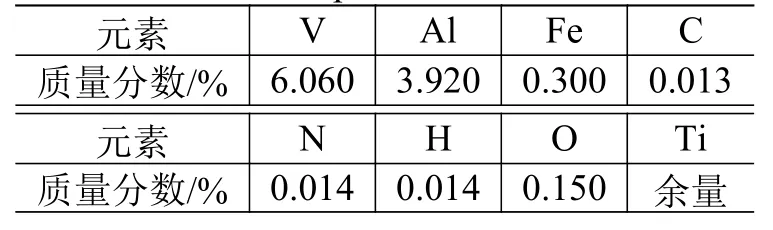
元素 V Al Fe C质量分数/% 6.060 3.920 0.300 0.013元素 N H O Ti质量分数/% 0.014 0.014 0.150 余量

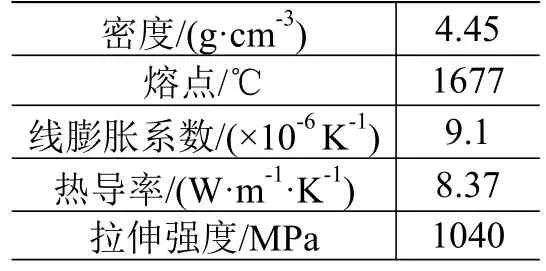
表2 TC4 钛合金的热物理和力学性能Table 2 Thermal-physical and mechanical properties of TC4 titanium alloy

2 表面张力贮箱焊接残余应力计算

本文研究所用的球形表面张力贮箱外壳内径为 889 mm、厚度 1 mm[7]，其中心（赤道位置）有一条环形焊缝。通过有限元软件ANSYS采用shell 181单元建立贮箱外壳的1/4有限元模型，在贮箱边界施加对称约束，材料弹性模量取110 GPa、泊松比取0.34[8]。

焊接采用双面拼接焊，热源为高斯热源[9]。使用ANSYS有限元分析软件对贮箱外壳进行焊接过程计算，得到贮箱外壳的焊接残余应力分布如图3所示：焊缝附近的焊接残余应力最高，为566.783 MPa，并随着与焊缝中心距离的增加而快速减小，最小值为-176.383 MPa（负值表示应力方向沿垂直焊缝平面向内，下同）；但由于夹持板的压力，焊接残余应力在焊缝两边各出现一个小幅度的升高，其局部极大值为-45.987 MPa。图4为焊接残余应力在垂直于焊缝方向上的分布示意。

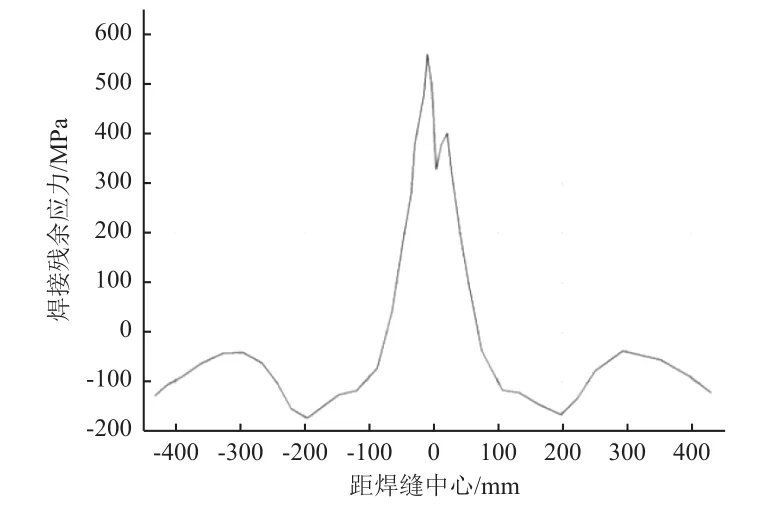
图3 焊接残余应力分布曲线Fig.3 Distribution of welded residual stress

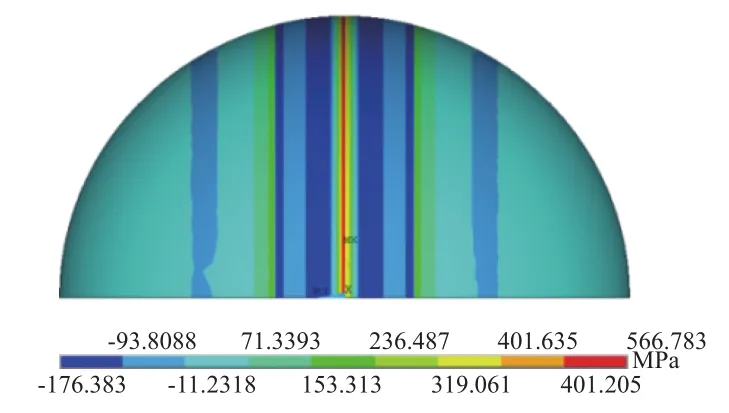
图4 焊接残余应力垂直于焊缝方向的分布Fig.4 Welded residual stress distribution on tank

由于球形贮箱的厚度与内径比约为1/1000，在10 mm范围内弧度变化极小，可将其视为平板结构进行分析，将模型导入Simufact Welding软件中进行焊接过程计算，图5为贮箱右半部的焊接残余应力在垂直于平板焊缝方向上的分布，图6为平板焊缝附近的焊接残余应力仿真分析结果。

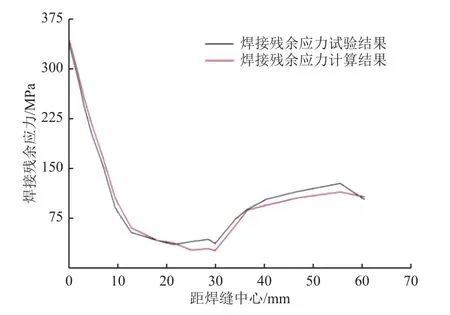
图5 焊接残余应力分布曲线Fig.5 Welding residual stress distribution

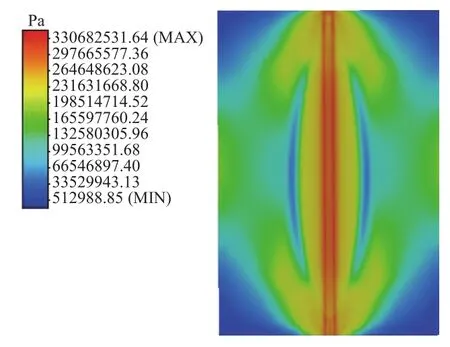
图6 平板焊接残余应力分布Fig.6 Welding residual stress distribution on welded plate

从图5中可以发现：在焊缝中心所残余的焊接应力较大，达到了330.682 MPa，之后沿垂直于焊缝的方向逐渐减小，最小值为5.13 MPa；但在距焊缝中心40～50 mm处由于存在夹持工装，在夹持应力的影响下，该区域的残余应力呈现出一个上升波动，其波峰的极大值为132.580 MPa。

3 焊接残余应力对应力强度因子的影响分析

3.1 应力强度因子计算

应力强度因子（SIF）是剩余强度和裂纹扩展计算中的基础参数，表征裂纹的特征、应变场的强度、应力大小及能量，并且代表裂纹扩展能力的高低，应力强度因子越大裂纹就越容易扩展。因此，确定应力强度因子在计算裂纹构件剩余疲劳寿命中起着非常重要的作用。

在Franc3D中引入有限元模型，如图7所示，在距离平板的中心0.2 mm处，插入半径为0.2 mm的初始裂纹并结合ANSYS重新划分网格，其裂纹平面垂直于平板，对应力强度因子KI、KII、KIII进行求解，结果如图8所示。

图7 裂纹网格划分模型Fig.7 Finite element model with crack

图8 应力强度因子分析Fig.8 Comparison ofKI,KII,KIII

从图8可以看出，在焊接残余应力的作用下，主要影响参数为应力强度因子KI，其最小值位于归一化裂纹前沿数值为0.5，即裂纹中心处，；且KI值沿裂纹呈凹型分布趋势，裂纹两端的数值较高，。KII与KI的分布趋势相同，但比KI的数值小很多；KIII基本呈随着归一化裂纹前沿数值的增加逐渐增加的分布趋势。

3.2 不同裂纹角度的影响

分析裂纹与焊缝呈不同夹角对于应力强度因子的影响：初始裂纹平面与焊缝平行，将裂纹平面进行顺时针旋转，分析其与焊缝顺时针夹角α分别为 10°、15°、20°时的裂纹应力强度因子KI、KII的变化情况，结果如表3所示。

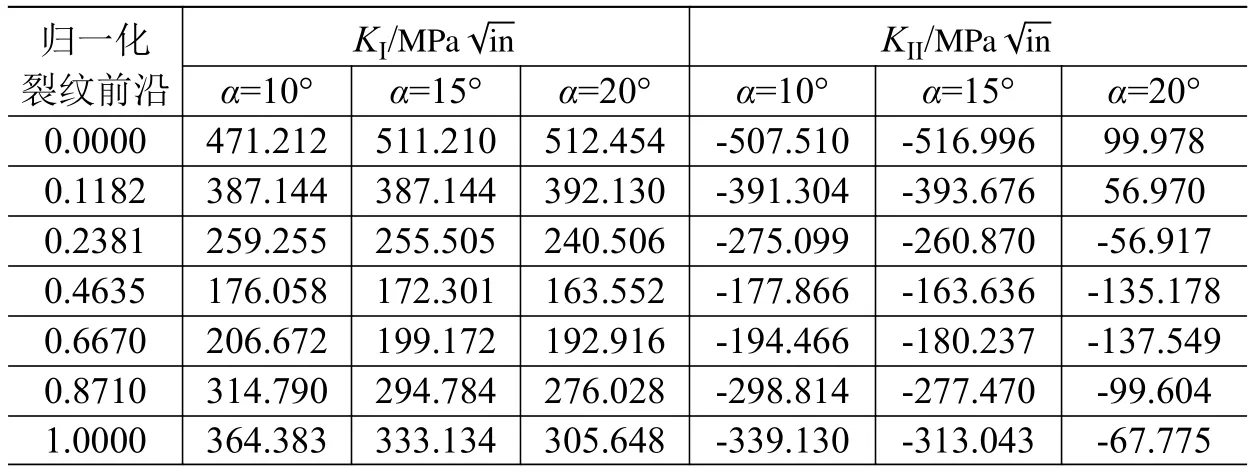
表3 裂纹与焊缝夹角对应力强度因子的影响Table 3 Comparison of SIF for different crack angles

图9和图10分别为裂纹与焊缝成不同夹角下的应力强度因子KI和KII计算结果。

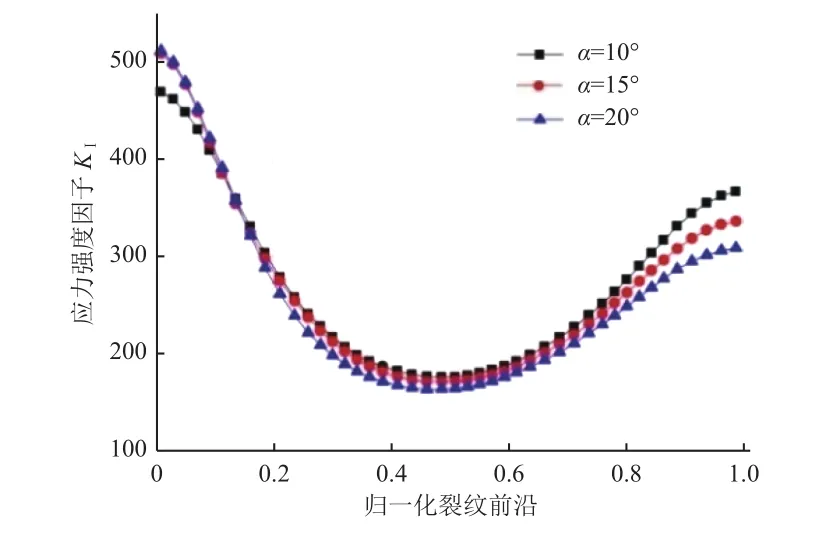
图9 裂纹与焊缝夹角对应力强度因子KI 的影响Fig.9 Comparison ofKI for different crack angles

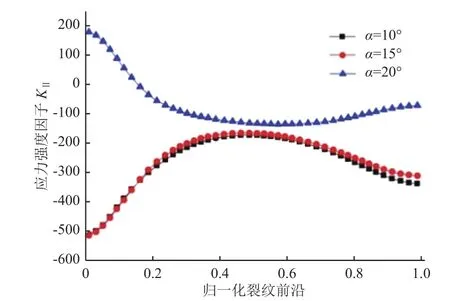
图10 裂纹与焊缝夹角对应力强度因子KII 的影响Fig.10 Comparison ofKII for different crack angles

由图9可见：KI值随夹角的变化并不明显，夹角为 10°、15°、20°时，KI值均随着归一化裂纹前沿数值的增大先减后增，在归一化裂纹前沿数值为0.5（即裂纹中心）处达到最小值。由图10可见：KII值在裂纹与焊缝夹角为10°和15°时变化不大，均呈随着归一化裂纹前沿数值的增大先增后减的趋势，在裂纹中心处达到最大值；但当夹角增加到20°时，KII值发生剧烈变化，其整体分布趋势也发生反转，变为先减后增，裂纹中心处变为最小值。

3.3 裂纹尺寸系数的影响

椭圆裂纹尺寸主要由半长轴长度a和半短轴长度c确定。为分析不同裂纹尺寸对应力强度因子计算结果的影响，对a/c值分别为1和2的裂纹（a=0.2 mm、c=0.2 mm 和a=0.4 mm、c=0.2 mm）进行应力强度因子KI、KII的计算，结果如表4所示。

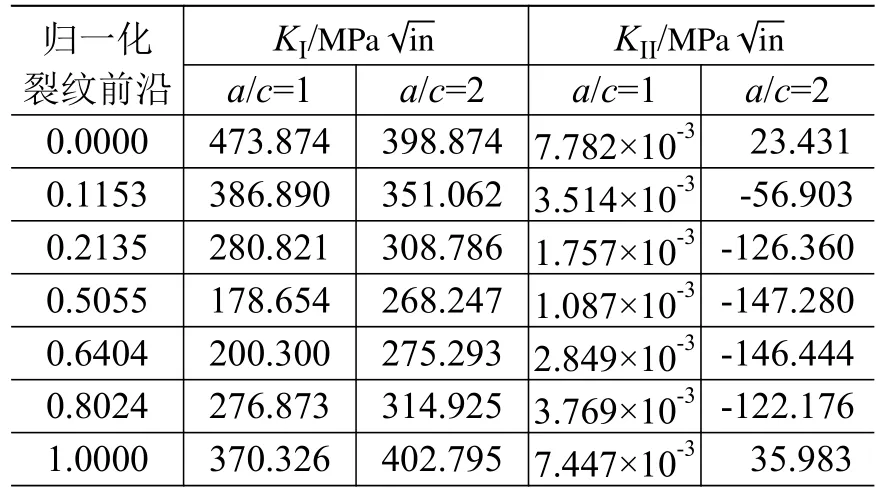
表4 裂纹尺寸系数对应力强度因子的影响Table 4 Comparison of SIF for different crack axes ratios

图11为裂纹尺寸系数对应力强度因子KI的影响：裂缝半长轴从0.2 mm增大到 0.4 mm时，KI值整体增大，变化幅度显著减小，最小值都出现在归一化裂纹前沿数值为0.5，即裂纹的中心位置处。图12为裂纹尺寸系数对应力强度因子KII的影响：裂缝半长轴从0.2 mm增大到 0.4 mm时，KII值整体减小，变化幅度显著增大，在裂纹中心处应力强度因子变化较为缓慢。

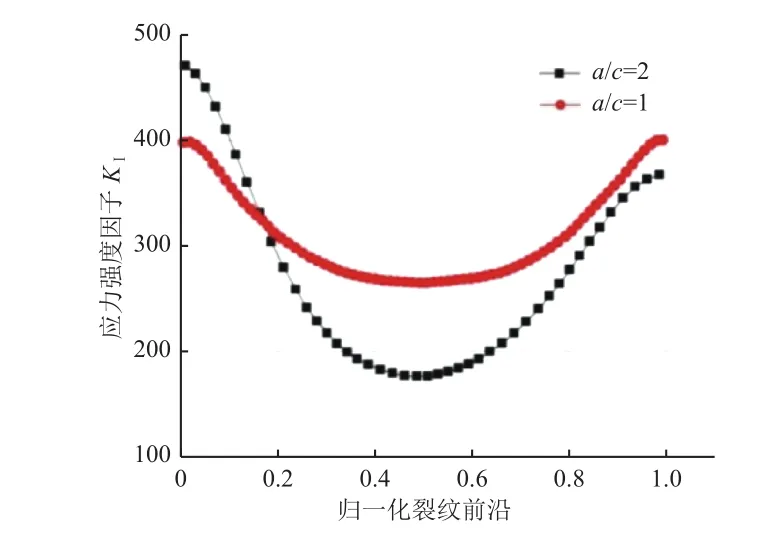
图11 裂纹尺寸系数对应力强度因子KI 的影响Fig.11 Comparison ofKI for different crack axes ratios

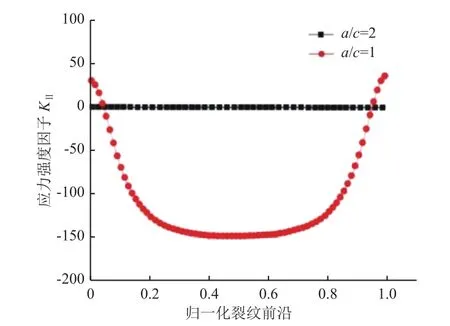
图12 裂纹尺寸系数对应力强度因子KII 的影响Fig.12 Comparison ofKII for different crack axes ratios

4 结论

为了分析焊接残余应力的影响，对焊接残余应力下的贮箱既有裂纹进行分析，计算应力强度因子KI、KII、KIII的数值变化情况，研究不同的裂纹形态对于应力强度因子数值的影响，结论如下：

1）在焊接残余应力作用下，起主要作用是应力强度因子KI，其随着裂纹归一化前沿数值的增加呈先减后增的趋势，裂纹中心处的KI值最小，裂纹沿两边的扩展速率大于裂纹中心的扩展速率。

2）裂纹与焊缝的夹角对于应力强度因子KI的影响较小；对于KII，在夹角较小时影响较小，但角度一旦超过一定的值，KII值的整体变化趋势就会发生较为剧烈的改变。

3）随裂纹a/c比值的减小，应力强度因子KI值整体增大，但其沿裂纹的变化趋势变缓；KII则恰好相反，随a/c比值的减小，KII值整体减小但变化幅度增大；KI和KII的最小值都在裂纹中心处。