航行体近水面滑跳运动试验研究

孙士明,陈玮琪,王宝寿,郁 伟,何振民,季锦梁

(中国船舶科学研究中心国防水动力学重点实验室,江苏无锡214082)

0 引言

水面滑跳是航行体近水面小角度撞水过程中所发生的一种特殊运动，人们常见的“打水漂”就是一种典型的滑跳现象。近年来不断有学者提出利用这种滑跳运动来实现近水面高速机动飞行的新概念跨介质飞行器[1-4]，成为跨介质航行体研究的热点问题之一，其连续滑跳的关键在于如何保持撞水过程中的姿态稳定。但是，跨介质航行体近水面滑跳问题涉及到复杂的多相流动与航行体大幅运动的相互作用，尤其是航行体高速撞水过程中带来的航行体受力的剧烈变化及自由液面的破碎与飞溅等问题，具有强烈的非线性。目前对于水面滑跳的研究多集中在物体运动过程的数值仿真[5-6]，而实际情况中，滑跳运动是否可行则少有试验研究涉及。本文通过开展近水面高速滑跳航行体试验研究，探究航行体水面滑跳运动特性，为近水面跨介质飞行器的研制提供技术基础。

1 水面滑跳构型设计

1.1 滑跳模型外形与尺度

自身平衡而稳定的气动布局可有2种选择：一种是正常的飞机形式，一种是鸭式布局形式[7]。一般高速滑行艇采用的都是鸭式布局形式，为了能够以较小的速度快速完成水面滑跃，本文试验模型采用鸭式布局。

航行体总体布局如图1所示，在弹体主体的中后部加装楔形体滑行面，以实现航行体触水滑跳过程减阻和降载，滑行面斜升角25°，并与航行体主体部分结合在一起，保证光滑过渡。航行体前部装有小型翼，用于贴近水面时提供部分升力及保持模型平衡。模型总长为960 mm，滑行面宽度400 mm，模型设计为正浮力，总体重量9.6 kg，静浮于水面时的状态如图2所示。

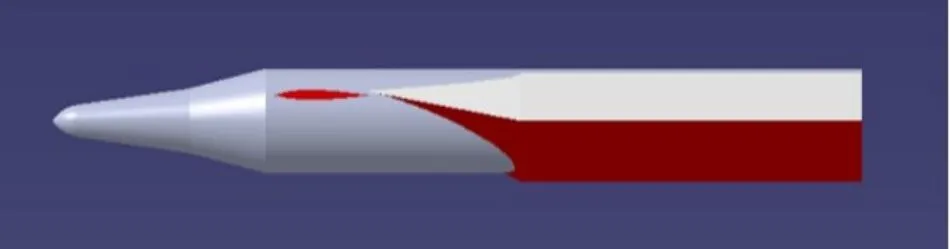
图1 滑跳模型示意图Fig.1 Schematic of skipping model

图2 滑跳模型静浮于水面时状态Fig.2 Floating state of skipping model

1.2 模型重心参数影响计算与分析

针对该模型，本文进行了初步数值仿真。因为数值计算不是本文研究的重点，故对计算方法仅作简单介绍。本文计算采用基于求解RANS方程的CFD方法[8]，湍流模型选取标准模型，采用VOF多相流模型进行自由界面捕捉，使用六自由度求解器结合重叠网格方法实现模型的大自由度运动。采用有限体积法对控制方程进行离散，压力场求解采用SIMPLE算法。计算域总网格数约240万。

计算工况为模型以30 m/s速度从距水面0.1 m高度位置释放，模型受到150 N恒定推力，作用位置在航行体尾部截面中心位置。计算中变化的参数为模型重心的纵向和垂向位置。图3显示了不同推力矩条件下模型滑跳过程倾角变化规律，推力矩主要反映了模型垂向重心位置的影响规律，可看出推力矩对模型运动的影响显著，甚至完全改变模型撞水后的姿态变化方向。通过综合比较，本文选取模型撞水后可以保持姿态相对稳定的参数，即推力矩为1 N力矩时的重心垂向位置参数。

图4显示了模型不同重心纵向位置对滑跳过程的影响。重心位置一般应靠后布置，本文计算了模型重心在中后部距柱段前缘288 mm、338 mm和388 mm三个位置参数。通过计算发现，模型实现稳定滑跳过程存在一个最佳重心范围，最终本文选定重心纵向位置距柱段前缘338 mm位置参数。

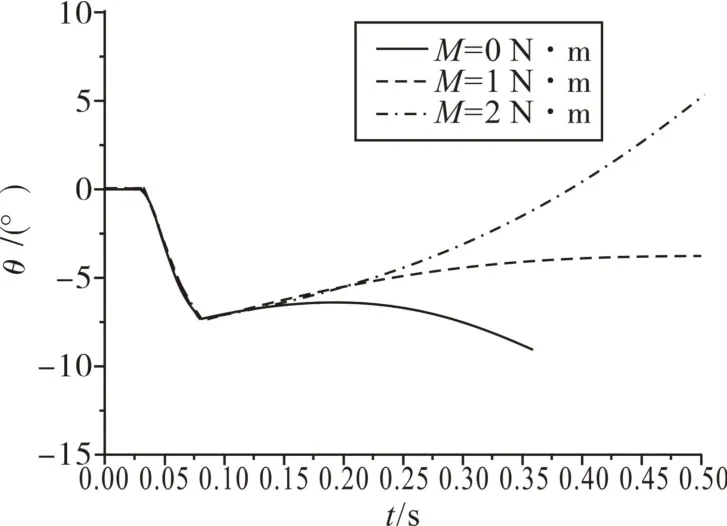
图3 不同推力矩条件下模型滑跳过程倾角变化Fig.3 Variations of trim angle under different thrust moments

图4 不同重心纵向位置模型滑跳过程倾角变化Fig.4 Variations of trim angle under different longitudinal positions ofmass center

从以上计算结果中可以看出，滑跳模型对于重心位置的布置非常敏感，因此在模型设计时应加以重点考虑。图5显示了通过计算分析选取合适参数后的模型触水滑跳过程，可以看出，滑跳过程模型倾角变化很小，不会对下一次滑跳过程的初始姿态参数产生很大变化，即可以保持相对稳定的滑跳过程。

图5 模型水面滑跳过程仿真结果Fig.5 Simulation results of skipping process ofmodel

2 水面滑跳试验

2.1 滑跳运动方式可行性验证

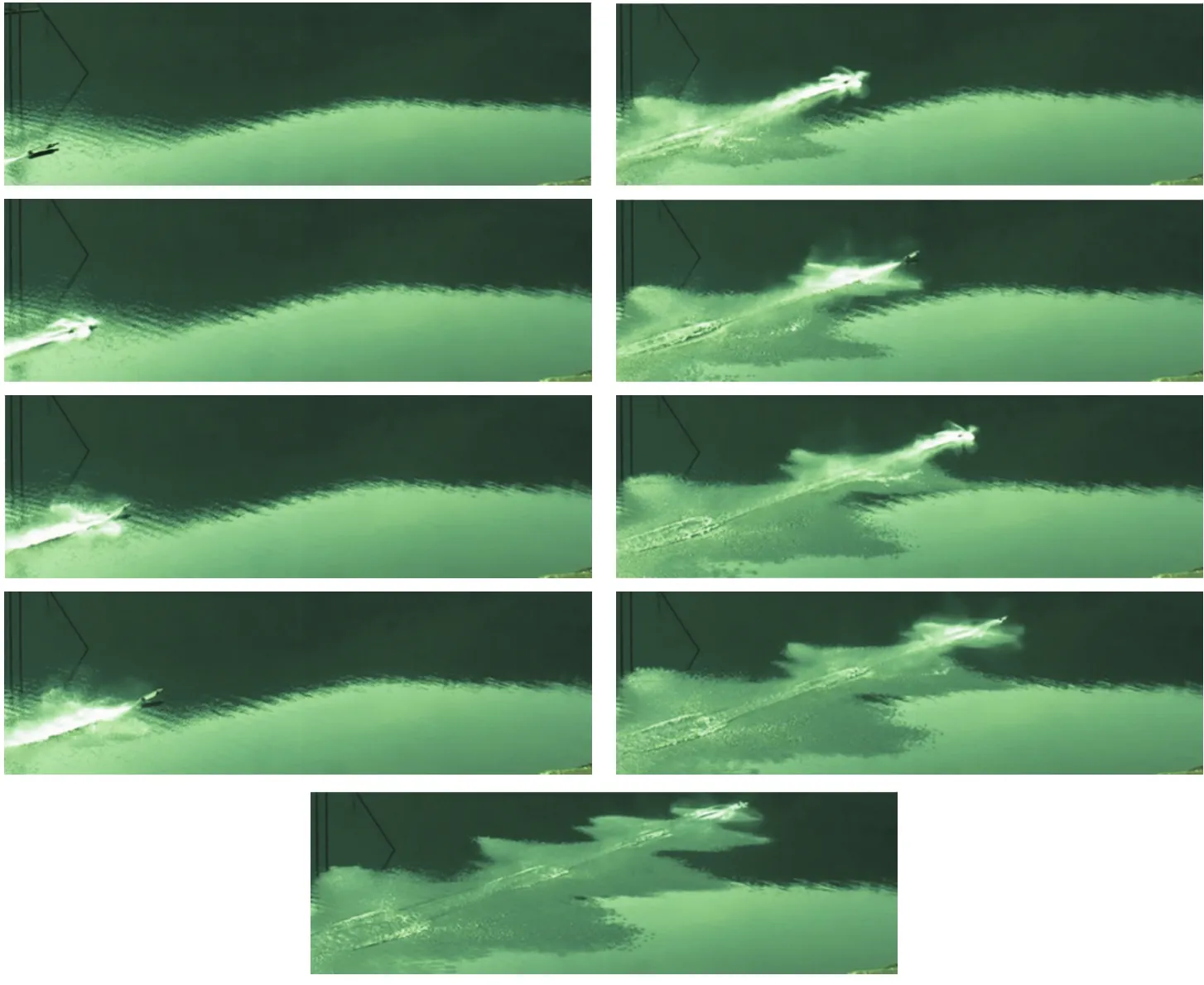
图6 航行体模型水面滑跳过程Fig.6 Skipping process of vehiclemodel on water surface

基于本文设计的滑跳构型，开展了开放水面自由滑跳试验，模型整个运动过程如图6所示。通过试验录像可以看出：模型可以保持连续滑跳的稳定性，稳定滑跳次数达到4次以上；模型整个运动过程基本保持直线运动，没有发生明显的侧倾；运动速度达到预期目标，通过图像判读，模型速度在第二次与第三次撞水之间达到最大值，最大速度约为29.0 m/s，弹跳高度也在此段时间内最大，距水面约0.3 m；滑跳过程中，模型撞水产生的飞溅比较明显，模型失去动力后，速度降低，在第四次滑跳后降至可滑跳最小速度之下，未能继续滑跳。该试验基本验证了本文设计的模型可以实现连续稳定的滑跳运动。

2.2 滑跳运动稳定性及液面飞溅分析

图7 航行体滑跳倾覆过程Fig.7 Capsizing process of skipping

在滑跳模型设计过程中，通过计算发现模型重心会对滑跳过程产生明显影响，试验中亦同样发现这一现象，当模型重心有所改变时，会影响滑跳过程模型触水时刻的倾角，当倾角过大时，会引起滑跳的不稳定性。如图7所示，模型以较大倾角撞水时(图中倾角为26°)，尾部会先触水产生很大的力矩，使模型姿态迅速变化，转变为低头再次撞水，这样的2次连续击水过程使模型失去滑跳稳定性，甚至产生倾覆。本文由于试验次数较少，不能定量提出倾角稳定范围，但从少数发生倾覆的试验工况来看，初步认为撞水倾角超过25°会产生倾覆。因此，滑跳模型的设计应仔细考虑模型重心位置，确保撞水过程不至产生很大的倾角。

图8 未改进前航行体滑跳过程产生的液面飞溅Fig.8 Water splash of unmodified model in skipping process

横向稳定性同样是滑跳稳定的一个重要问题，本文试验模型受构型限制，横滚方向转动惯量较小。试验中也发现外界扰动较小时，模型可以稳定向前滑跳，而当运动过程受到明显侧风影响时，模型易受横向扰动影响而产生侧倾，进而影响滑跳稳定。后期可通过加装机翼来增加横向稳定性。

图9 采用一体化构型后航行体滑跳过程产生的液面飞溅Fig.9 Water splash of modified model in skipping process

下面对滑跳过程中的液面飞溅情况进行初步分析。图8和图9显示了2个工况下模型一次滑跳过程中撞水及液面飞溅过程，2个工况使用的模型有所不同。图8中模型楔形体滑行面与弹体之间通过一平面直接连接，而图9中模型则将画面与弹体之间通过光滑过渡面连接，使模型实现一体化构型。从图8中可以看出，由于尾喷流的作用，模型撞水产生的飞溅流场较为复杂，由于模型主体与滑行板连接过渡段不是光滑过渡，导致撞水过程中该处产生强烈的飞溅，并将其与模型主体产生的飞溅分割开来(如图8中红色圆圈位置所示)。因此，在后续滑跳模型的设计上，应尽可能减少部件之间不光滑的连接过渡，以减小产生的飞溅尺度。从图9(为了更清晰地看到整个液面的变化过程，高速录像从模型运动路线的侧后方拍摄)中可以看出，模型采用一体化构型后，飞溅没有了图8中那样被“割开”的现象。由于滑行面形状为楔形体，尾部滑板撞水过程产生的飞溅主要向两侧发展，尾喷流会对滑跳产生的飞溅产生比较明显的影响，形成复杂的多相流动。

3 结束语

本文针对航行体滑跳运动开展研究，设计了一种适宜滑跳的航行体构型，对航行体的布局进行了初步探讨，并开展水面自由滑跳试验。试验表明：①本文设计的滑跳模型能够实现水面连续稳定滑跳，最高速度达到约29 m/s，最大弹跳高度约0.3m，证明了滑跳运动方式具有一定的可行性；②滑跳模型对重心位置变化非常敏感，滑跳运动过程中应尽可能保持小倾角条件，并且模型整体应该保持光滑过渡。本文的研究仅是对滑跳运动现象的初步探索，后续可在以下2个方面继续深入开展相关研究工作：

1)滑跳模型的进一步改进。本次试验受试验条件限制，对设计的构型进行了一定程度的简化，试验速度也并不很高，未来可继续对构型开展优化，以降低滑跳过程液面飞溅带来的能量损失，并不断提高试验速度以进一步验证滑跳运动在更高速度条件下的可行性。

2)增加模型的主动控制手段。目前试验条件下均采用无控模型，若能通过一些简单有效的控制手段来调整模型撞水过程中的姿态变化，将更有利于模型多次滑跳过程的稳定性。