固体火箭发动机燃气射流噪声数值模拟

彭文均

(海装武汉局,湖北武汉430064)

0 引言

固体火箭发射过程中，在尾喷管出口形成了高速、高温、高压的非稳态复杂燃气流场以及与周围的大气剧烈掺混形成震耳欲聋的燃气射流噪声，对周围人员和环境都可能带来损伤，且不利于火箭武器系统的隐蔽性，甚至影响发射的安全性[1]。在设计火箭发动机过程中，采取准确的计算方法预测射流噪声的分布特性，对于优化火箭发动机性能具有指导性意义。超音速燃气射流噪声的形成机理比较复杂，具有较强的非线性，目前仍是燃气射流研究的难点之一。

Gely[2]等对Ariane5运载火箭发射噪声进行了测试，并分析了发射噪声的主要形成机理。Krothapalli[3]等对超音速热射流气动噪声进行了实验研究，通过对近场和远场的测试获得了声场特性。Cacqueray[4]等采用大涡模拟方法详细描述了高温超音速燃气射流的流场特性，通过等熵线性欧拉方程和完整欧拉方程求解远场声压。Hixon[5]等人采用CFD方法和Kirchhoff积分法结合起来计算了近场中均匀流的噪声，远场噪声可由Kirchhoff积分法得到。在国内，胡声超[6]等人采用大涡模拟对多喷管射流流场进行了三维非稳态数值模拟，根据流场的湍流特性选取积分面，利用FW-H方程计算远场的噪声。马宏伟、刘礼军[7]采用小波分析方法对便携式火箭的脉冲噪声测试数据进行了分析，描述了强噪声的传播规律。徐强[8]对单室双推力实验发动机射流近场噪声进行了测试，并分析了噪声的频谱特性。

本文主要对尾喷管超声速燃气射流噪声进行数值仿真，并分析超声速射流流场和声场的基本特性。

1 计算模型与求解方法

计算模型如图1所示，计算区域由喷管、尾管及外流场组成。由于火药在燃烧室内部燃烧生成燃气流动，在喷管出口产生欠膨胀超声速燃气射流，流出尾管后进一步向外面大气环境膨胀，因此计算区域应包含燃气湍流脉动较大的区域。计算区域轴向为尾管直径的45倍，径向为尾管直径的25倍。对高速可压缩燃气射流来讲，边界条件的处理对流场结构和特性有较大的影响。根据计算区域边界的物理特征分为以下4种边界条件。

1)入口边界条件。

喷管入口是发动机燃烧室燃气的出口，同时也是本文计算区域的入口边界，根据实验数据设定入口压力边界，取16.5 MPa。

2)出口边界条件。

计算区域的出口边界设定为压力出口，选取环境参数。

3)壁面边界条件。

计算区域中的壁面边界包含喷管壁面和尾管壁面，采用绝热、无滑移壁面条件，选用标准壁面函数处理边界湍流。

4)内部边界。

内部声源面设置为内部边界条件，并定义声源面内和面外为不同区域名称，以便在计算中对声源面进行选择。在此边界上参数通过内部插值传递。

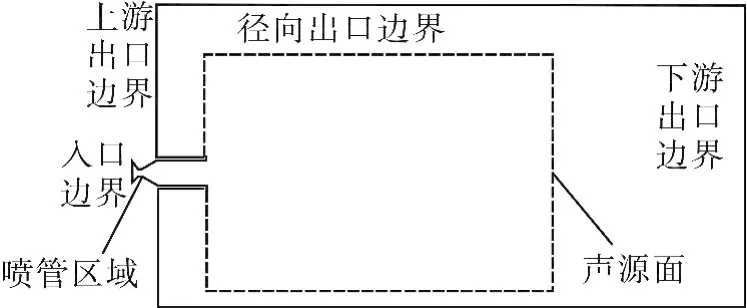
图1 计算区域示意图Fig.1 Schematic diagram of computational domain

将整个计算区域划分成多个子区域，使得结构网格保持较好的正交性，并对喷管、尾管及声源面内部进行加密处理。通过对网格的无关性检测发现，当网格数目达到约80万时，燃气射流流场的变化极小。噪声监测点位置分布是以喷管出口中心点为圆心，半径为r的圆弧上，噪声监测点位置的半径与射流方向的夹角称为方向角，射流方向为0°方向角。

采用LES方法对射流流场进行数值计算。LES方法的主要思想是采用滤波函数对瞬态N-S方程进行滤波，将流场变量分成大尺度涡运动和小尺度涡运动，对大尺度涡运动进行直接数值模拟，而由于小尺度涡运动具有局部平衡性，可以通过建立合适的亚网格模型来模拟进行假设求解。滤波后得到可压缩流连续方程、动量方程为

在获取流场信息后，采用FW-H声学方程对射流噪声进行数值计算[9-10]。FW-H声学方程是将连续方程和动量方程推导为非均匀波动方程的形式，其表达式为

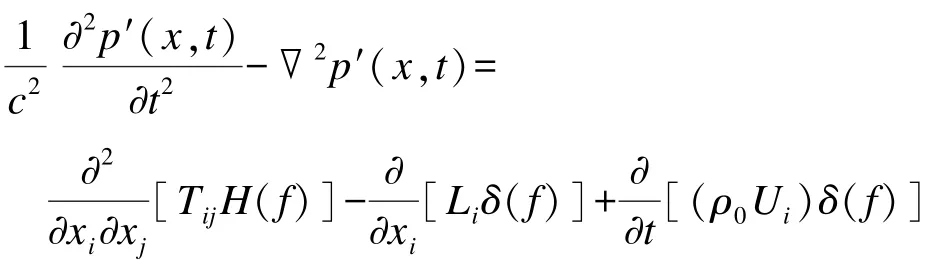
式中：Ui=[1-(ρ/ρ0)]vi+(ρui/ρ0)，Li=Pijnj+ρui(un-vn)；c 为声速；p′为远场声压；Pij、u 表示流体的应力张量、速度；v为物面速度；Tij为莱特希尔(Lighthill)应力张量；H(f)为 Heaviside函数；δ(f)为狄拉克(Dirac delta)函数。

2 计算结果与分析

为了较准确地预测超声速射流噪声，首先需要对射流流场进行模拟，获得射流流场的湍流特性。图2给出了欠膨胀超声速燃气射流瞬时流场的压力分布云图。从图中可以看到，高温高压燃气出尾管后，在大气中迅速膨胀，沿着轴向膨胀最充分的处静压低于环境压力，在射流边界形成反射的压缩波。通过这样的循环，在射流流场形成了不断交替并强度逐渐弱化的膨胀压缩波结构。

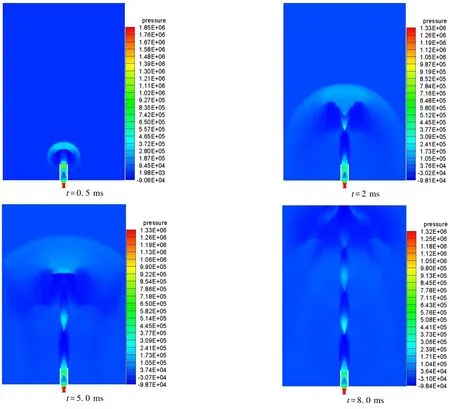
图2 射流的瞬时压力分布云图Fig.2 Distribution nephogram of transient pressure of jet flow

图3为燃气射流噪声的计算值与实验值的比较。从图中可以看出燃气射流噪声的计算值和实验值随方向角的分布规律一致，在方向角45°时射流噪声声压级最大，并在计算范围内随着方向角度的增大呈递减。声压级从方向角45°到115°降低了14.7dB，具有明显的指向性，主要是由于燃气在不同方向的能量分布不均匀所致[11-12]。计算值与实验结果吻合较好，在射流上游方向角最大115°处，两者的声压级相差最大，大约为2.6 dB，即相对误差仅为2.4%，说明了射流噪声数值模拟方法比较准确。

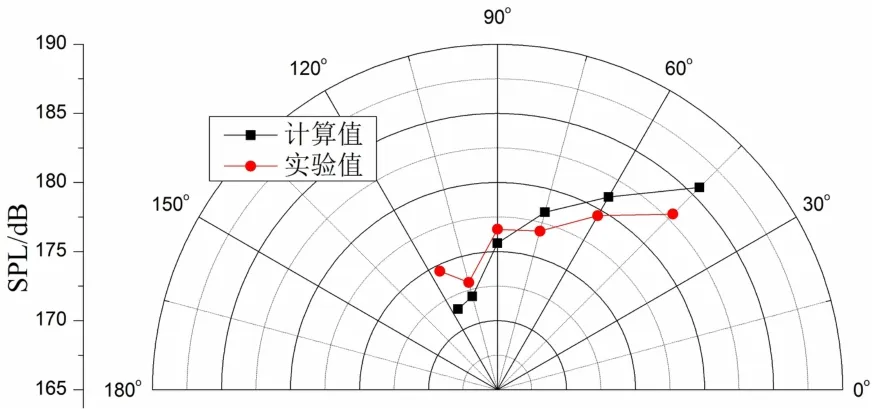
图3 射流噪声计算与实验结果的比较Fig.3 Comparison between calculation and experiment resluts of jet noise

图4为不同燃烧室压力条件下燃气射流在方向角45°处产生的噪声频谱。发动机工作过程中，超声速燃气射流噪声主要表现在低频区。随着燃烧室压力的增大，燃气射流噪声声压级明显增大，但噪声频谱分布规律基本不变。图5为不同燃气温度条件下的噪声频谱，从图中可以看出燃气温度对射流噪声影响较小。

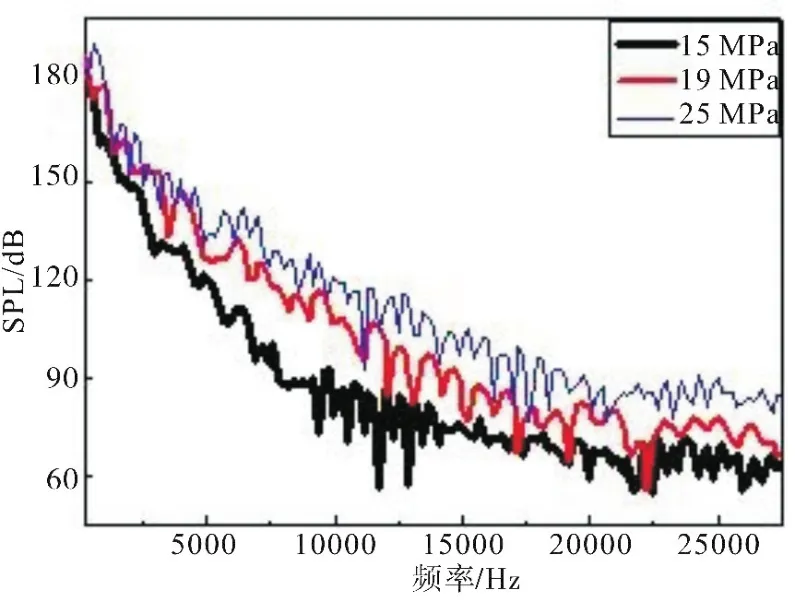
图4 不同燃烧室压力的噪声频谱Fig.4 Noise frequency spectrums of different chamber pressures

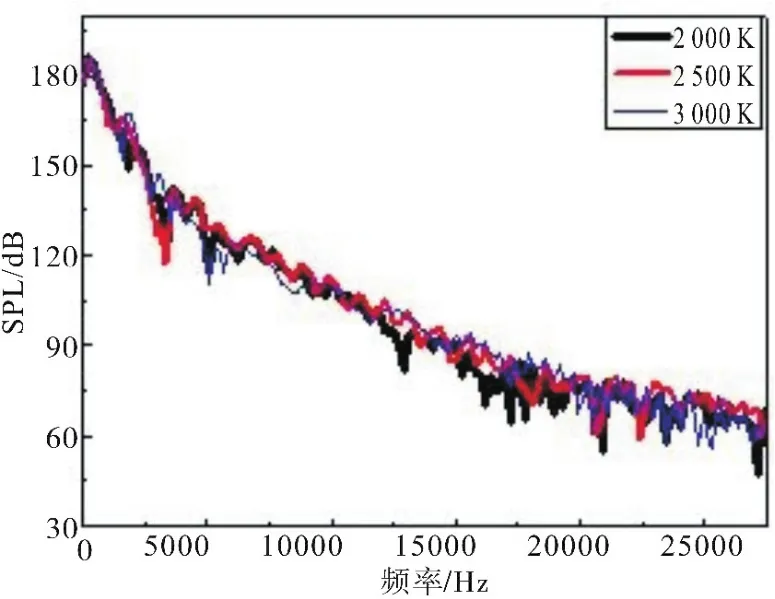
图5 不同燃气温度的噪声频谱Fig.5 Noise frequency spectrums of different gas temperatures

3 结束语

1)对火箭发动机欠膨胀超声速燃气射流噪声进行了LES/FW-H耦合的数值计算，超声速射流声场的计算结果与实验测试结果在空间分布上一致，计算值与实验值的相对误差仅在2.4%以内，验证了本文理论计算的正确性。

2)发动机工作过程中，由于射流噪声源逐渐向下游移动，射流噪声声压级随着方向角的增大而减小，在45°方向角时噪声最大，具有较强的指向性。3)燃烧室压强越大，超声速射流噪声声压级越大，射流噪声主要表现在低频特性，燃气温度对射流噪声影响较小。