降低受信仪行程开关返程误差方法的分析

刘 威,吴建萍

(中国船舶重工集团有限公司第七一〇研究所,湖北宜昌443003)

0 引言

火箭发射装置是弹药发射平台，属于海军重要装舰设备。由于该装备具有旋回、俯仰等功能，并配有控制设备，随时根据战术要求调转发射装置。受信仪作为发射装置的传感设备，具有反馈装置运行位置和控制装置运行、射界范围的功能[1-2]。为了控制发射装置在一定范围内工作，受信仪设计采用了凸轮条和微动开关滚轮的相对运动来控制微动开关通断，实现对装置运行、射界的控制。在实际工作中，受信仪的行程开关返程误差较大，一般在1.0°～1.5°之间波动，影响了运行、射界范围的控制精度。

本文主要围绕如何降低凸轮行程开关返程误差展开研究，针对影响行程因素多，各因素存在交叉影响的实际问题。主要采用PDCA程序，应用了因果图分析方法，将凸轮行程开关的返程误差减小到0.5°以下，提高发射装置运行、射界范围的定位精度，达到了预期的目标。

1 工作原理

1.1 工作过程数学模型

根据受信仪结构特点，建立工作过程的数学模型。将凸轮往返的2个过程分解开，2个过程凸轮运行角度差为凸轮的返程误差。

1)当微动开关由松弛到压紧的过程。

此过程主要是凸轮盘带动凸轮条绕凸轮盘定轴作圆周运动，微动开关位置相对于凸轮盘定轴位置固定，微动开关处于松弛状态；凸轮条圆周运动过程中，凸轮条一边接触微动开关滚轮，滚轮向上抬起，微动开关被压缩实现接通或切断控制电路，从而控制运行、射界范围。工作原理图见图1。

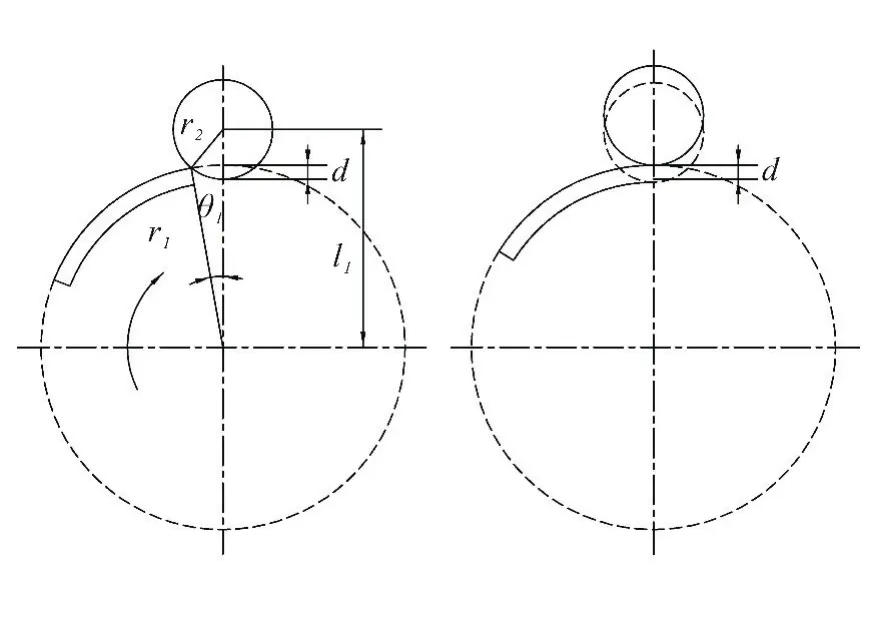
图1 凸轮行程开关工作原理图(一)Fig.1 Working principle diagram of cam liMit sWitch(1)

图1中：r1表示凸轮条的外径；r2表示微动开关滚轮的外径；d表示微动开关的压缩量；θ1为当微动开关由松弛到压紧过程中凸轮的转动角度；l1表示微动开关在松弛状态时凸轮圆心与滚轮圆心的距离，此时由松弛要进入压缩状态：

由三角形余弦定理，可得

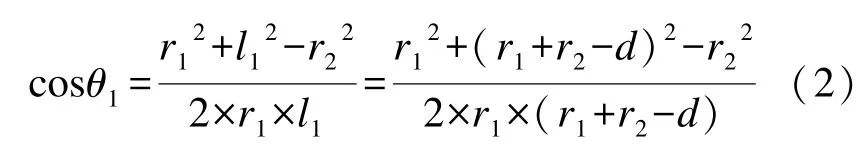
2)当微动开关由压紧到松弛的过程。

此过程主要是凸轮盘带动凸轮条绕凸轮盘定轴作圆周运动，微动开关位置相对于凸轮定轴位置固定，微动开关处于被压缩状态；凸轮条圆周运动过程中，凸轮条一边离开微动开关滚轮，滚轮向下运动，微动开关被释放实现接通或切断控制电路，从而控制运行、射界范围。工作原理图见图2。

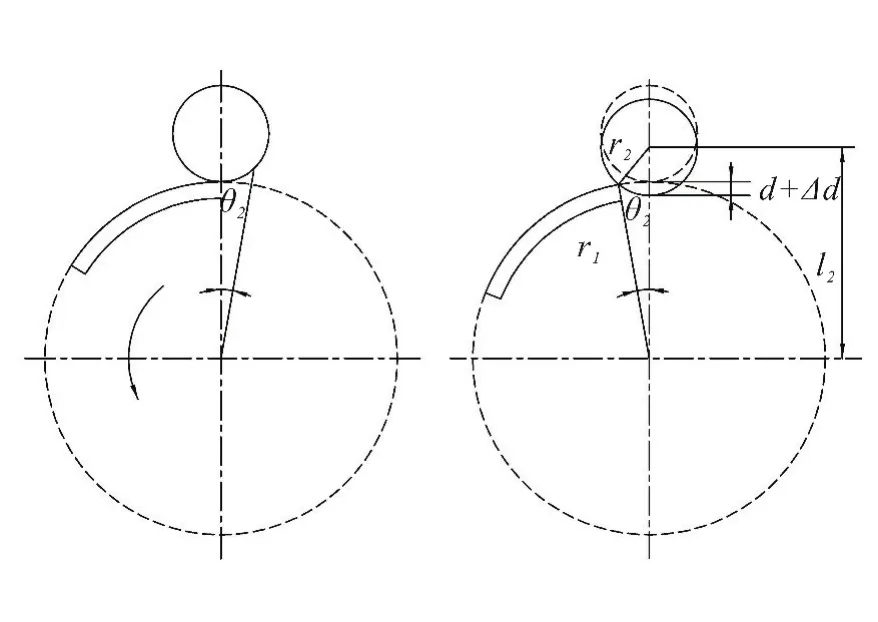
图2 凸轮行程开关工作原理图(二)Fig.2 Working principle diagram of cam liMit sWitch(2)

图2中：Δd表示微动开关的差动量；l2表示微动开关在松弛状态时凸轮圆心与滚轮圆心的距离，此时从压缩回到松弛状态：

由三角形余弦定理，可得

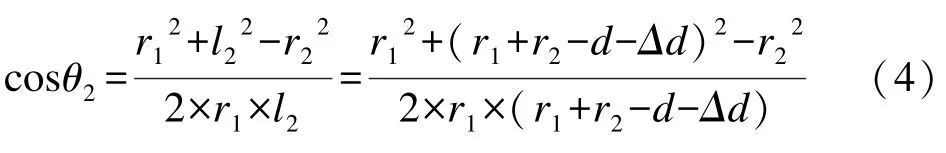
式中Δθ表示凸轮往返过程的回程差，可得：

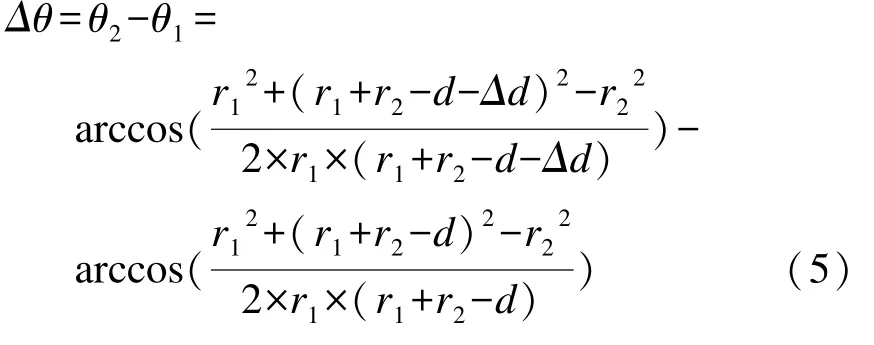
1.2 仿真计算

依据公式(5)，往返过程的回程差Δθ影响因素主要包括凸轮条的外径r1、微动开关滚轮的外径r2、微动开关的压缩量d、微动开关的差动量 Δd等。在MATLAB仿真软件平台中，计算出回程差Δθ与各参数之间关系。

r1与Δθ的关系曲线见图3，其中；r2=4 mm，Δd=0.5 mm，d=2 mm；r2与 Δθ的关系曲线见图4，其中 r1=62mm，Δd=0.5mm，d=2mm；d与Δθ的关系曲线见图5，其中 r1=62 mm，r2=4 mm，Δd=0.5 mm；Δd与 Δθ的关系曲线见图6，其中r1=62 mm，r2=4 mm，d=2 mm。

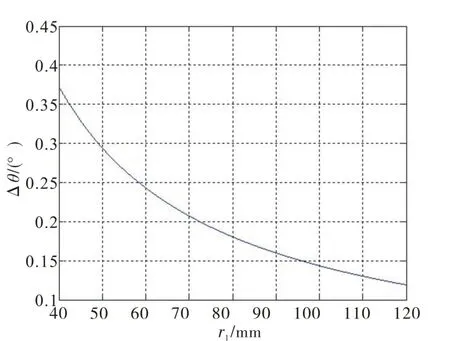
图3 变化曲线图(一)Fig.3 Change curve diagram(1)

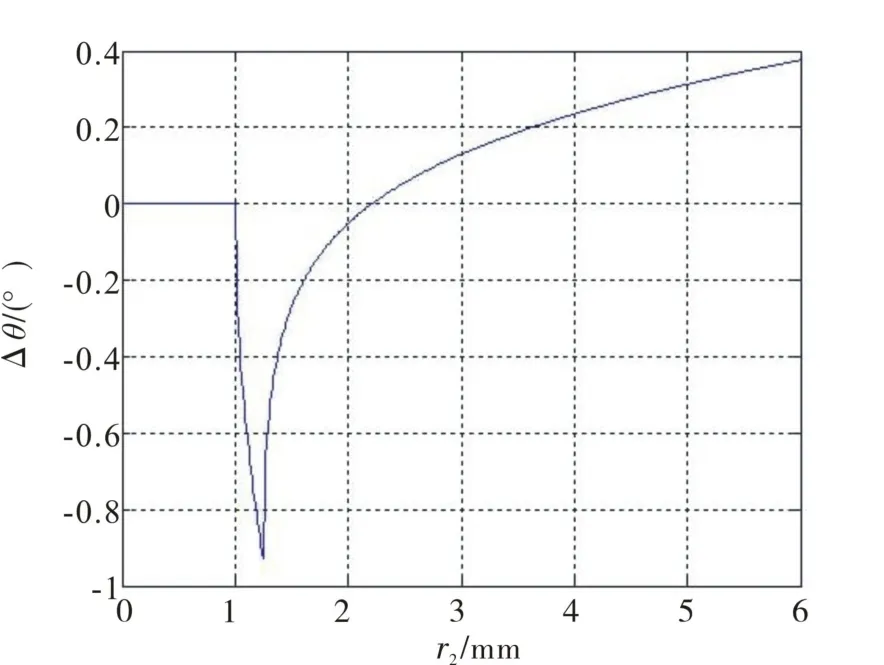
图4 变化曲线图(二)Fig.4 Change curve diagram(2)

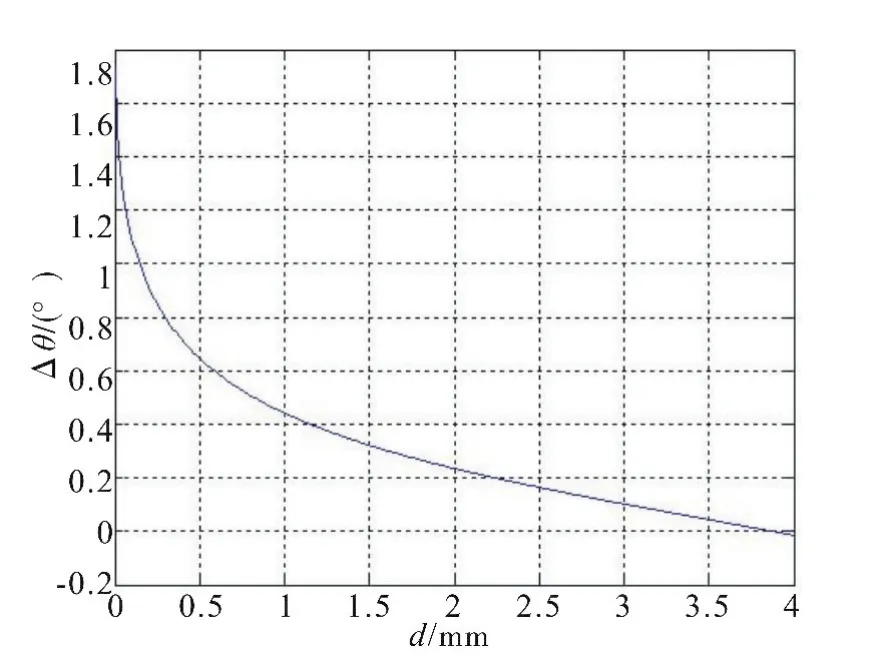
图5 变化曲线图(三)Fig.5 Change curve diagram(3)

由图3-6可得：

1)r1变大时，Δθ变小，即在其它条件不变的情况下，凸轮的外径变大，凸轮条往返过程的回程差变小。

2)r2在(0 mm，2mm)区间上时，r2≤d=2 mm，凸轮条上边缘线直接压在微动开关滚轮轴线上，无法实现压缩微动开关滚轮，Δθ仿真计算数值无实际意义。依据经验，一般要求r2≥2d，保证凸轮条压缩微动开关滚轮的过程顺利完成。当d=2 mm，确立有效工作区间为(4 mm，6 mm)，在此区间内，微动开关滚轮变大时，凸轮往返过程的回程差变大。

3)d变大时，Δθ变小，即在其它条件不变的情况下，微动开关的压缩量变大，凸轮条往返过程的回程差变小。

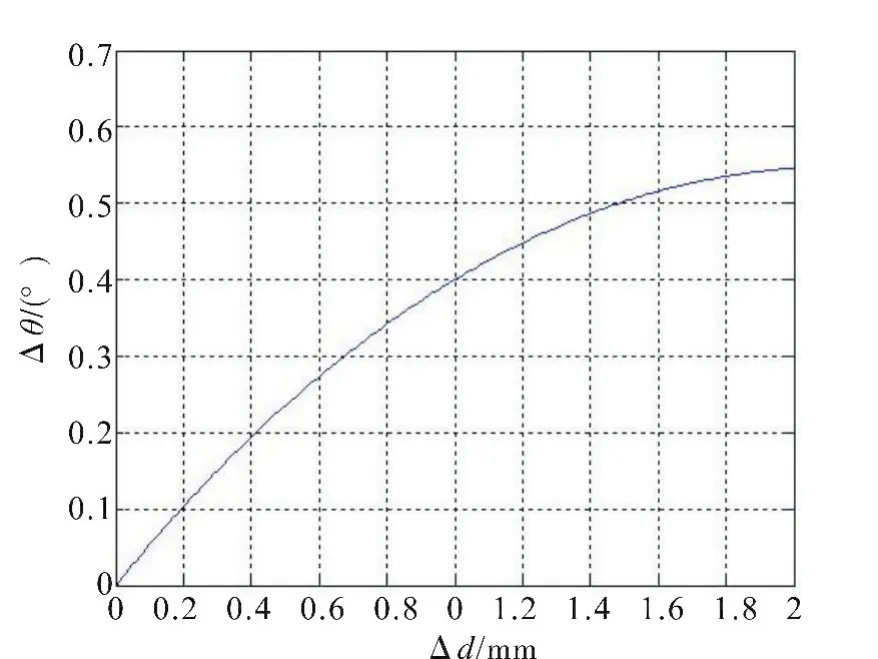
图6 变化曲线图(四)Fig.6 Change curve diagram(4)

4)Δd变小时，Δθ变小，即在其它条件不变的情况下，微动开关的差动量变小，凸轮条往返过程的回程差变小。

由以上 4条结论，可知通过调节r1、r2、d、Δd等参数可以降低Δθ，使其满足目标要求。

1.3 优化求解

复合形法是求解约束优化问题的一种重要的直接解法。它的基本思路是在可行域内构造一个具有个顶点的初始复合形。对该复合形各顶点的目标函数值进行比较找到目标函数最大的顶点(称最坏点)，然后按一定的法则求出目标函数有所下降的可行的新点，并用此点代替最坏点，构成新的复合，复合形的形状每改变一次，就向最优点移动一步，直至逼近最优点[3-5]。

受信仪行程开关返程误差优化目标是误差值最小，同时保证r1、r2、d、Δd等参数满足物理尺寸要求。 令r1=X(1)、r2=X(2)、d=X(3)、Δd=X(4)，由公式(5)构造复合形法的目标函数为

获得上述目标函数和约束函数后，可按下述步骤开展复合形法迭代直接求解[6-7]。

1)根据作图法给定搜索区间a和b，随机产生K个随机点，然后将非可行点调入可行域内，构成初始复合形；

2)计算各顶点的函数值，选出好点X(L)与坏点X(H)；

3)计算除坏点外其余各顶点的中心点X0；

4)计算映射点X(R)；

5)构成新的复合形；

6)判断终止条件，各顶点与好点的函数值之差的均方根值小于误差值ε：

如不满足迭代条件，则返回步骤2)继续下一次迭代；否则，可将最后复合形的好点X(L)及其相应的函数值T启动(X(L))作为最优解输出，并结束运算。

在MATLAB环境下，编写3个M函数，分别为主函数、目标函数和约束函数。经过MATLAB程序运行后，得到目标函数值的收敛曲线如图7。

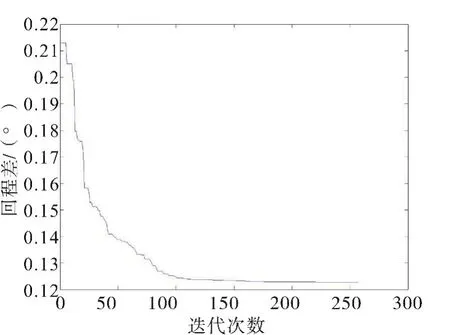
图7 目标函数值的收敛曲线图Fig.7 Convergence curve diagram of objective function value

图7可以看出，随着迭代次数增加，误差值逐渐减少，接近于最优解，直到误差小于规定值时，程序结束。 迭代 180次后，X(1)、X(2)、X(3)、X(4)、Δθ(X)变化极小，确定获得本次计算的最优解：

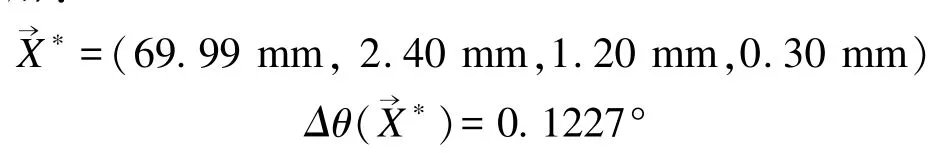
获得r1=70 mm，r2=2.4 mm，d=1.2 mm，Δd=0.3 mm受信仪的行程开关返程误差最小。

2 影响因素分析

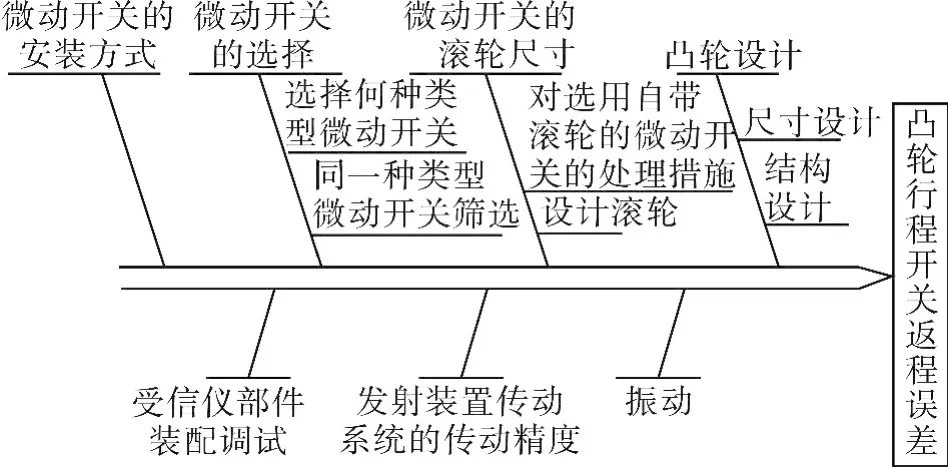
图8 返程误差影响因素因果图Fig.8 Causality diagram of effect factors of return errors

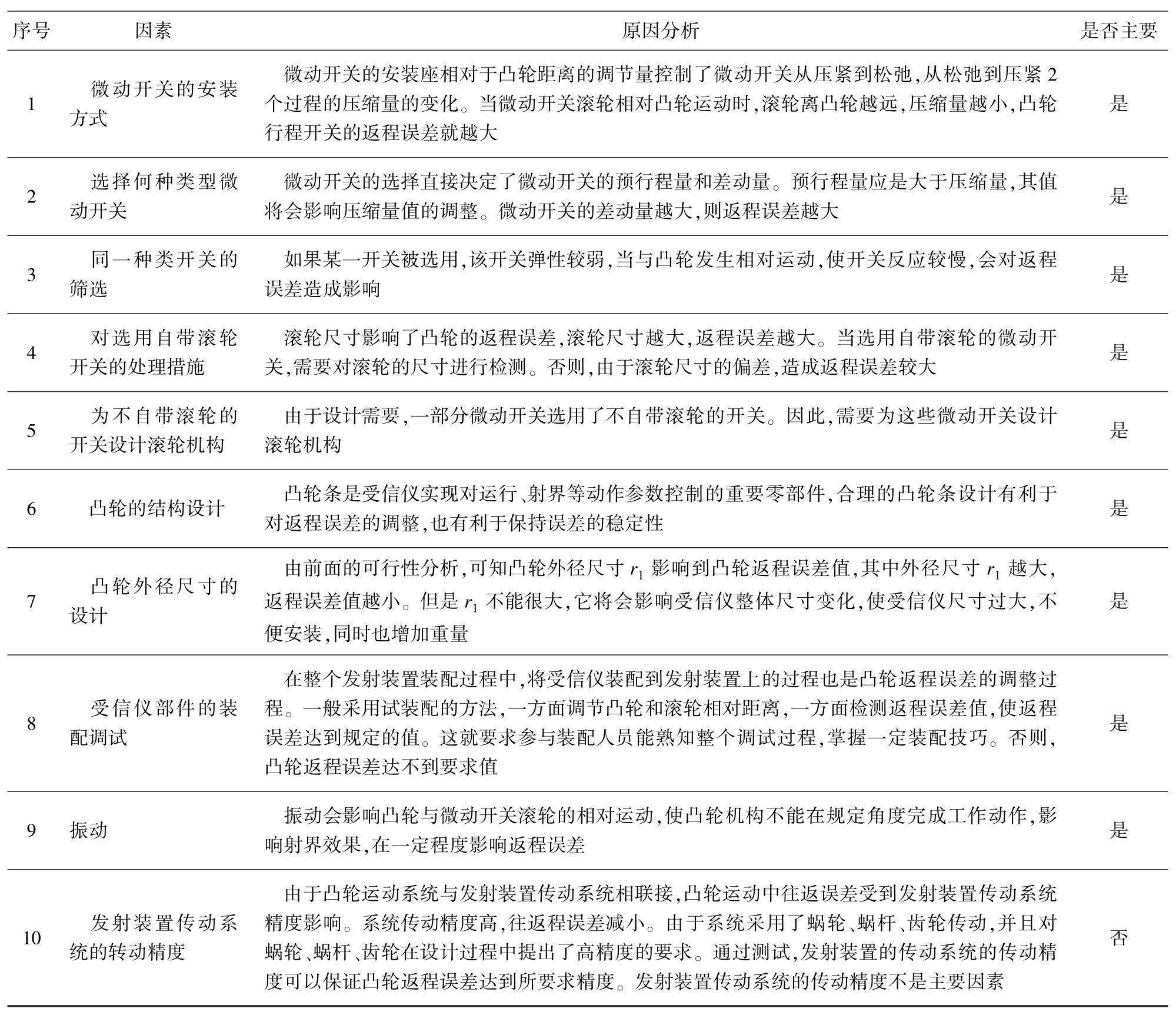
表1 影响因素分析说明表Table 1 Analysis specification of influencing factors

经上述分析，将凸轮行程开关的返程误差减小到 0.5°以下，不仅要求合理确定d、Δd、r2、r1等参数值，还要开展结构和机构合理设计，严控装配环节，从而消除各因素存在的交叉影响的实际问题。依据PDCA管理程序，采用了因果图分析方法，对影响凸轮行程开关返程误差因素进行综合分析，共找出10项因素[8-9]。各因素分析经归纳整理如图8所示。10项因素中，9项可列为引起误差的主要因素，1项作为非主要因素。见表1。

2.1 解决措施

措施一：改进微动开关的安装座结构设计。

将安装座螺钉孔由圆孔改为一字孔，一字孔的长方向应保证调整微动开关的滚轮与凸轮之间的相对距离，如图9-10。

措施二：选择适当类型的微动开关。

微动开关存在多种型号，微动开关种类及参数见表2。选取按钮和短转子2种型式，表2数据表明按钮和短转子2种型式预行程和差动量相对较小。

措施三：筛选开关。

对同一类型同批次开关筛选，因为其中可能有一部分开关弹性不足，可能会出现差动较大，应对开关进行选择。选出弹性有力开关，并由专人负责筛选，保证所用的每一个开关能够达到所需参数要求。

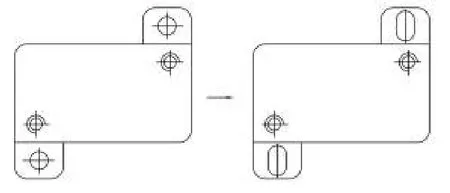
图9 安装座结构改进示意图Fig.9 Schematic diagram of improved install seat structure

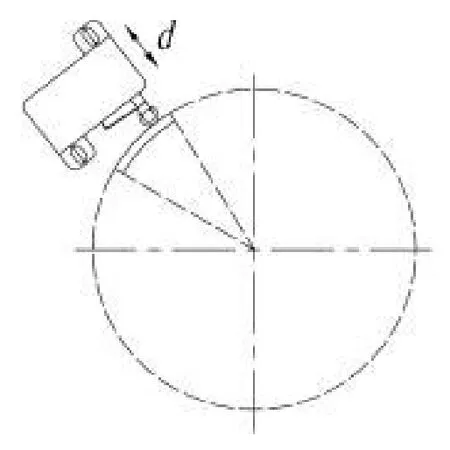
图10 固定座工作示意图Fig.10 Working schematic diagram of fixed seat

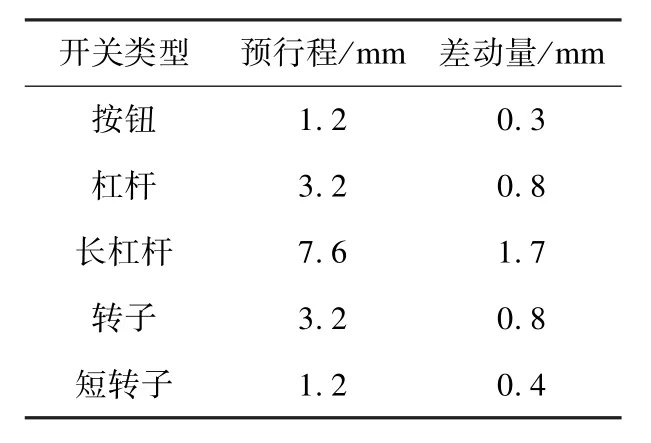
表2 微动开关参数表Table 2 Parameter table ofMicro switch

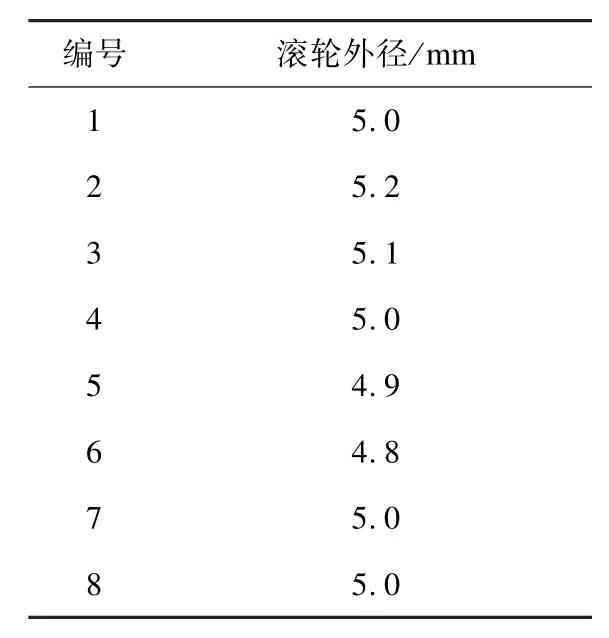
表3 滚轮尺寸检测数据表Table 3 Test data table of roller’s size

措施四：对选用自带滚轮的微动开关的处理措施。

当微动开关选择自带滚轮的微动开关，要对滚轮的外径尺寸进行测量，使被测滚轮外径尺寸小于8 mm。测量结果见表3。

表3中可得，所选的8个滚轮外径在4.8～5.2 mm之间，均小于8 mm，满足要求。

措施五：滚轮机构设计。

当选择不自带滚轮的微动开关，应对微动开关设计一套滚轮机构，如图11。

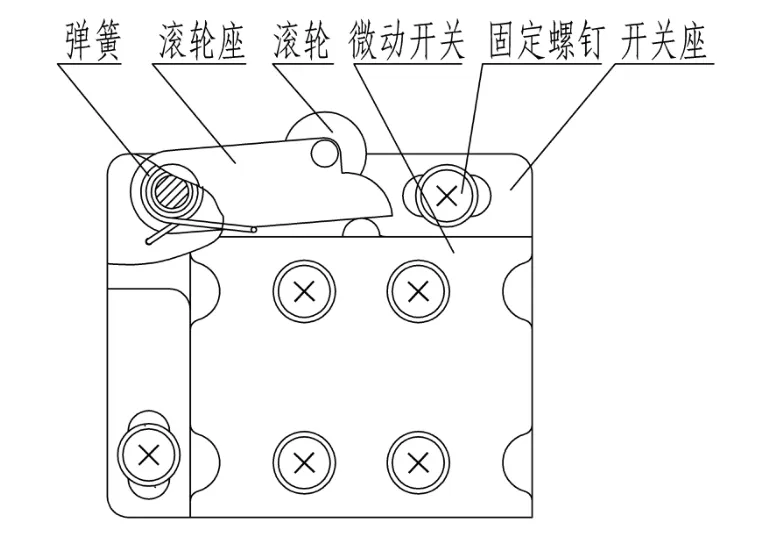
图11 滚轮机构示意图Fig.11 Schematic diagram of roller mechanism

其中，滚轮半径尺寸要小于或等于4 mm，使此机构满足设计要求。

措施六：凸轮结构设计。

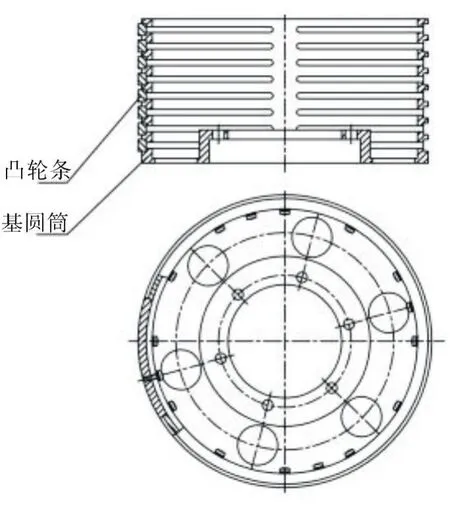
图12 凸轮机构示意图Fig.12 Schematic diagram of cam mechanism

凸轮采用凸轮片与基圆筒相结合方式，如图12。将凸轮片固定在基圆筒上，可以保证牢固可靠，防止凸轮条滑动。采用该结构一方面有利于调整，另一方面结构简单，安装方便。

措施七：凸轮条尺寸的设计。

某型发射装置凸轮条外径尺寸取62 mm，依据优化设计结果，取外径尺寸为 70 mm，则r1=70 mm；根据微动开关的选择，可得d=1.2 mm；Δd=0.4mm；滚轮外径取上限植为r2=4mm，可得：

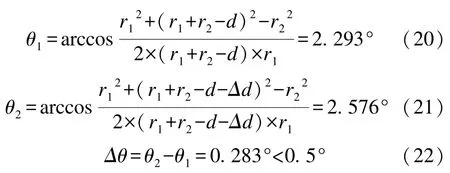
受信仪尺寸满足要求，最终设计尺寸为r1=70 mm。

措施八：受信仪部件装配调试。

在受信仪部件装配时要求保证受信仪转动灵活，在与发射装置装配过程中，采用了试装配法：不断调整微动开关的滚轮与凸轮片之间的距离，同时检测返程误差角度值。如表4。

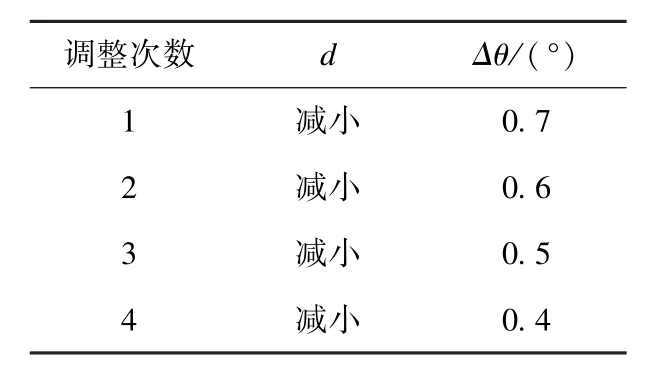
表4 安装过程调整表Table 4 Installation process adjustment table

措施九：防振。

采取防振动措施，主要从2个方面入手：一方面检查所设计的结构是否有防振动措施。由于发射装置具备运转过程中防振动措施：如缓冲器等，使本装置具备防振动措施；另一方面在发射装置运输过程中应有防振动措施。同时在装配调试阶段对微动开关的安装，微动开关安装座的固定，凸轮机构的装配进行检查，对装配中所用的螺钉进行拧紧检查。

2.2 验证效果

方向受信仪凸轮返程误差检测统计情况见表5，其中射界Ⅰ为射界范围下限点，射界Ⅱ为射界范围上限点；运行Ⅰ为运行范围下限点，运行Ⅱ为运行范围上限点；限速Ⅰ为限速范围下限点，限速Ⅱ为限速范围上限点。

高低受信仪凸轮返程误差检测统计情况见表6，其中射界Ⅰ为射界范围下限点，射界Ⅱ为射界范围上限点；运行Ⅰ为运行范围下限点，运行Ⅱ为运行范围上限点。

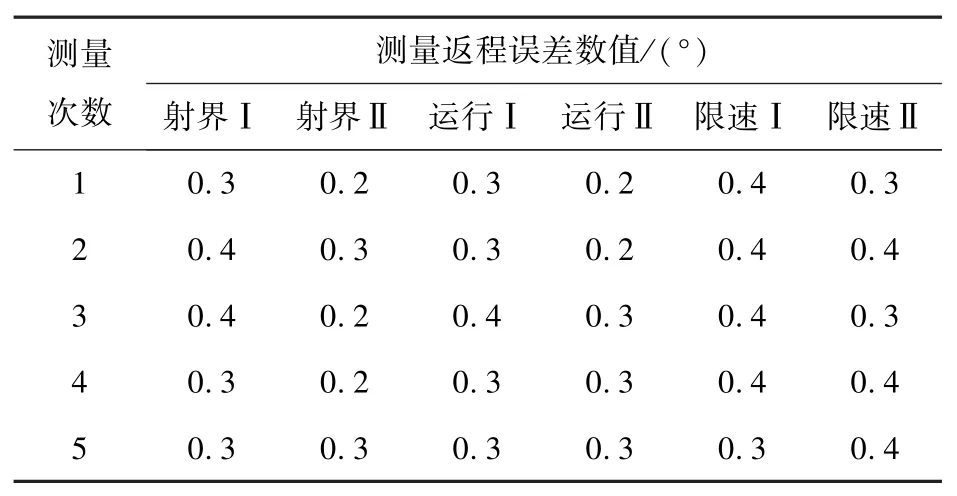
表5 方向旋回检测结果表Table 5 Test result of direction turn process

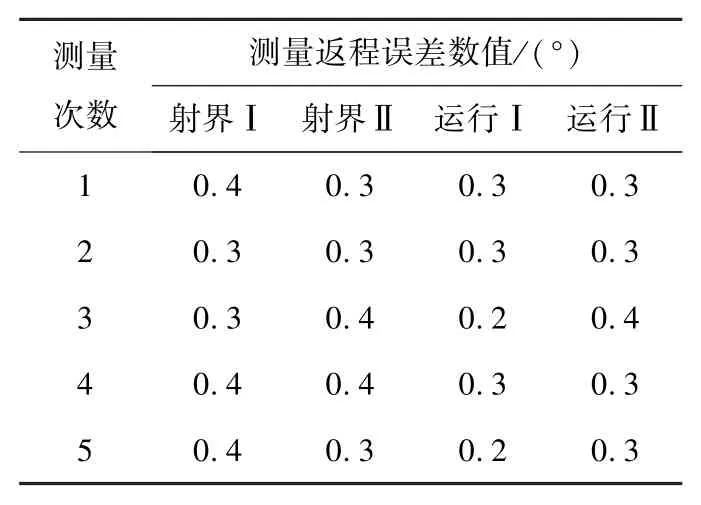
表6 高低俯仰检测结果Table 6 Test result of pitch angle

措施实施后，凸轮返程误差减小到0.5°以下。从表5、表6可以看出，方向旋回运行在射界、运行、限速等3种方式下和高低俯仰运行在射界、运行等2种方式下，经过检测凸轮返程误差均减小到0.5°以下，达到目标要求。

3 结束语

本文针对受信仪的行程开关返程误差较大实际问题，研究了受信仪的行程开关工作原理，建立了工作过程数学模型，采用复合形法开展了参数优化设计。结合PDCA程序，应用了因果图等质量管理工具获得影响误差主要因素，并逐一采取对应措施，将凸轮行程开关的返程误差减小到0.5°以下，提高发射装置运行、射界范围的定位精度，达到了预期的目标。