信号灯作用下的城市隧道路段交通流模型研究

王威，吴中

(河海大学土木与交通学院，江苏 南京 210098)

隧道是道路上常见的交通设施，隧道内外行车环境的差异会造成驾驶行为的不同，隧道路段的交通流特征也与普通路段有所差异，车辆在进出隧道时存在着减速和加速现象，并且隧道内车辆的行驶速度更慢。现有的隧道交通流的研究主要集中在高速公路隧道方面，学者更多地关注隧道驾驶行为研究以及微观仿真模型。林杉[1]建立了一种高速公路隧道元胞自动机模型，发现高速公路隧道会降低相应路段平均车速，同时对下游交通流起平滑作用；张蕾等[2]考虑了隧道路段的结构特征及限速特性，通过定量分析发现隧道所带来的交通延迟主要与交通流、隧道长度以及限速差值有关；Kirytopoulos等[3]在希腊对驾驶员进行问卷，研究驾驶员的驾驶行为和隧道安全措施，发现隧道内交通流与隧道灯光以及限速、安全距离关系紧密。林丽等[4]提出了一种计算加速度干扰的方法，对不同服务水平下隧道路段的城市隧道出入口拥挤情况进行研究，同时就实测数据以及仿真结果进行比对，得到交通流状态和加速度干扰之间的关系。

由于城市交通压力的增大以及土地资源匮乏，许多大中城市在城市内部修建隧道，城市交通流在信号灯的作用之下，呈现明显的间断流特征。龙小强等[5]引入交通流基本函数，推导出流量、密度、速度三者之间的关系，建立了间断交通流方程，并利用该方程研究了交通流经过信号交叉口演化的全过程。王殿海等[6]基于交通波理论，对交叉口车队的排队与消散过程及对上下游交叉口的影响进行了分析，同时就城市干道交叉口间的车队间隔及与信号协调之间的关系进行了研究，建立了相应的数学模型。唐铁桥等[7]考虑了信号灯的影响，改进了现有的跟车方程，得到了一个考虑信号影响的交通流模型，同时给出了其差分形式，通过数值仿真，对信号控制下的交通流的聚集、消散以及停车波、起动波的演化规律进行了研究。吴中等[8]在LWR模型的基础上，给出了空间二阶、时间一阶精度的数值差分模型，考虑了各子路段在不同信号灯下的不同路权特征，建立了黄灯前后边界条件，整体上很好地刻画了交叉口及相关道路交通流的时空变化情况。谭慧丽等[9]建立元胞自动机模型，通过设置信号灯，研究交通激波的形成和传播，发现对于一定的信号周期，流量会出现多个极值现象。傅白白等[10]通过VISSIM软件对交叉口进行仿真，基于仿真结果对信号设置进行优化。

在上述研究中，大多只考虑了信号灯或者隧道单一影响下的交通流特征，很少涉及隧道与信号灯共同作用下的交通流研究。隧道出入口与上下游信号灯的相对位置、上下游信号灯的相位差等因素对城市隧道路段的交通流都会产生一定的影响。

本文研究隧道与信号交叉口共同作用下的交通流特性。对城市隧道路段的交通环境特征及车辆跟驰特性进行分析；建立城市隧道路段的元胞自动机模型，并对单向双车道的城市隧道路段进行数值模拟，对比分析城市隧道路段的交通流时空图、基本图，研究隧道出入口位置设置、相位差等因素对路段交通流的影响。

1 城市隧道路段交通流特征

城市道路上的车流受到信号灯周期性的影响，总体现成队行进的车辆，在一队与另一队之间存在着明显的间隔。研究表明，间断流设施间隔3.2 km是足够产生连续流的距离[11]，而城市路网中很少有间隔大于3.2 km的相邻交叉口，因此，城市道路上的交通流体现为间断流特征。

隧道作为道路上的特殊路段，车辆在进出隧道的过程中，会产生一系列的视觉问题。白天车辆进入隧道时，由明转暗的“黑洞”现象；车辆驶出隧道时，由暗转明的“白洞”现象；驾驶员在行驶时需要时间适应这种视觉反差。尽管隧道中有照明设施的存在，“黑洞”、“白洞”现象依然会对隧道内行车产生一定的影响[12]。由于隧道内通风条件较差，车辆尾气聚集，隧道内能见度较差，为安全起见，驾驶员总采取较低的速度行驶，隧道内的行车速度总是低于隧道外面。此外，在正常情况下，隧道内是不允许随意变道和超车的。

对于城市隧道路段，由于信号灯相位的更迭，车队总是经常性地停车和重新起动，产生停车波及起动波；而车辆进出隧道的过程中，伴随着减速与加速的过程，产生减速波与加速波。当隧道出入口位置与交叉口之间的距离较短时，减速波与起动波、加速波与停车波传递的过程中可能会相互干扰，造成交叉口排队不能完全疏散或者拥堵等，这种影响与信号灯的相位差、交通量、绿信比以及信号灯与隧道出入口的相对位置都有着一定的关系。

2 信号控制下的城市隧道路段元胞自动机模型

本模型不考虑侧向进出对路段交通量的影响，建立如图1所示的城市隧道路段双车道元胞自动机模型，Lsig1、Lsig2为信号灯所在元胞位置，Lin、Lout为隧道进出口所在元胞位置，箭头为车辆的行驶方向，车辆在元胞路段上行驶按时间步长进行更新。

图1 城市隧道路段元胞自动机模型Fig.1 Cellular automata model of urban tunnel section

模型中共存在两类交通瓶颈：一类是交叉口瓶颈，其主要是在路段上某一点设置信号灯来周期性地控制车流通断，车辆在经过交叉口遇到红灯时需要经过停止和再起动的过程；另一类为隧道瓶颈，与交叉口瓶颈不同的是，隧道是路段上的一个较长瓶颈，除了由于隧道内部限速较低导致的车辆进出隧道时的减速和加速现象，隧道内较差的光线和视野，不确定因素较多，会更大概率地发生随机减速行为。

基于城市隧道路段的交通实际运行情况，在本模型中制定如下的交通规则[13]：

(1)在路段上存在着车辆限速，并且隧道内的车辆限速低于隧道外部；

(2)车辆行驶严格遵守信号灯规律，不考虑侧向交通的影响，绿灯时，车辆通过信号灯；红灯时，未通过信号灯的车辆停在信号灯前；

(3)在隧道内不允许车辆随意换道，隧道外部在满足一定的换道条件之后车辆以一定的概率进行换道；

在时间步t→t+1的过程中，城市隧道路段模型中车辆位置的更新步骤[14-15]如下：

Step1：车道变换

车道变换根据STNS模型[16-18]构造出对称双车道换道模型，并作一定的改进，增加了车道变换的位置条件，以适应隧道内部不能随意换道的规则；

位置条件：车辆位置xnLout；

换道动机：车辆与本车道前车间距dndn，其中，vn为本车速度，vmax为道路上车辆限速。

安全条件：车辆与目标车道后车的间距dn,other,back>dsafe，dsafe=vn,other,back，其中，vn,other,back为目标车道上后车的速度。

满足以上条件后，车辆以一定的概率pc进行换道。

Step2：加速规则

对应着驾驶员总期待着以最大速度行驶。

对于隧道外的车辆，即xnLout，车辆速度更新为vn→min(vn+a,dn,vmax)；

对于隧道内的车辆，即Lin≤xn≤Lout，车辆速度更新为vn→min(vn+a,dn,vtm)，其中，a表示车辆加速度，vtm表示隧道内车辆限速。

Step3：减速规则

由于前车阻挡或者信号灯的阻隔所造成的减速。对于车辆经过交叉口的规则，考虑二维元胞自动机模型BML模型[19]的中的减速规定，并进行一定的修改[20-21]，较为拥堵情况下，绿灯时车辆通过交叉口仍需考虑自身与交叉口的相对位置。

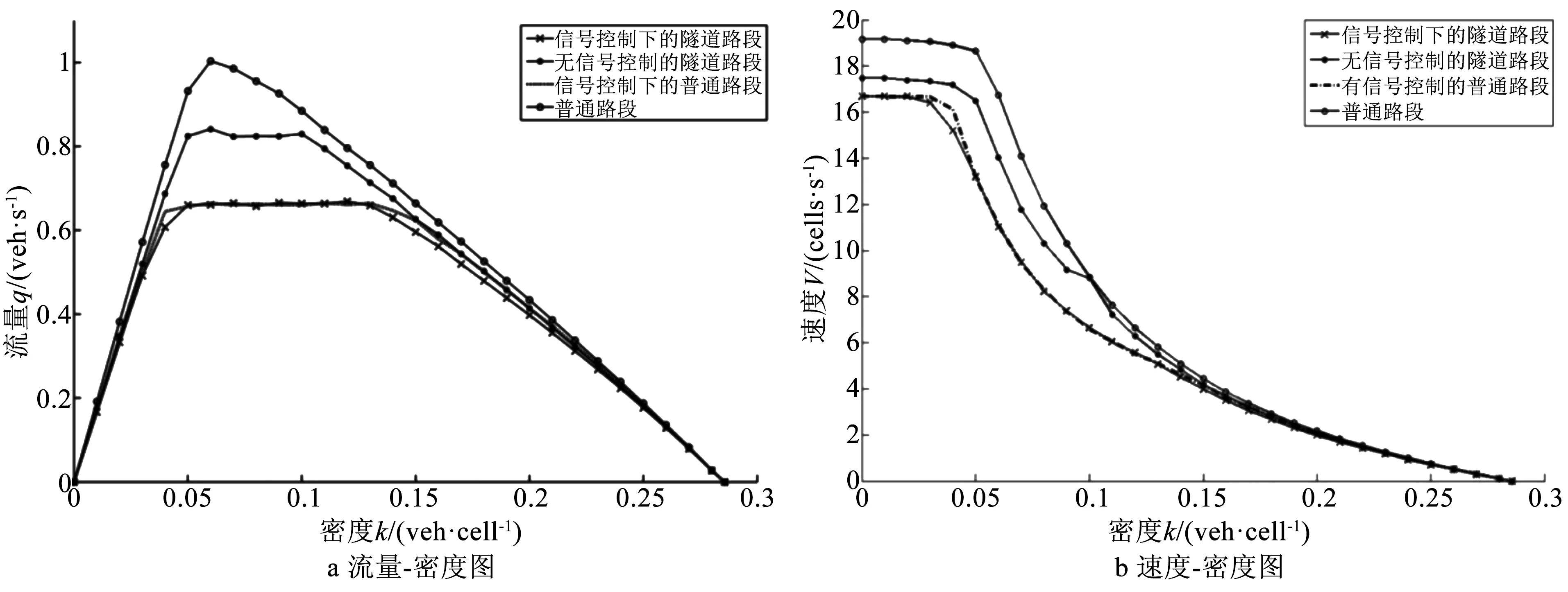
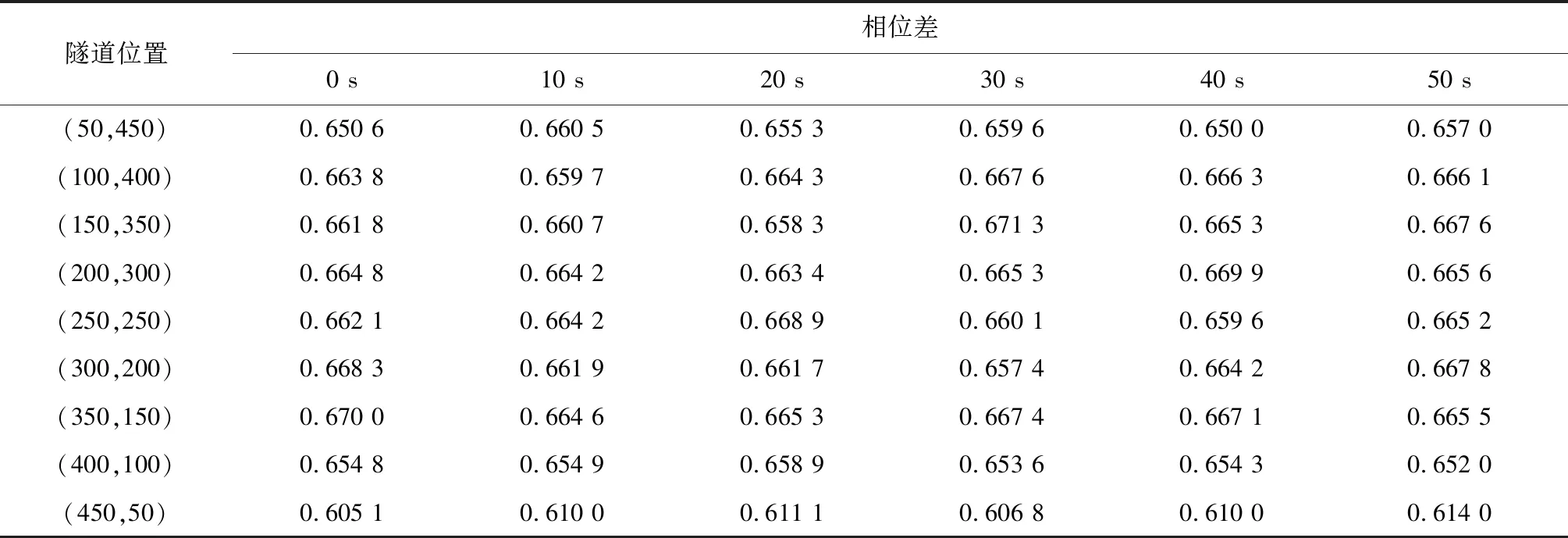
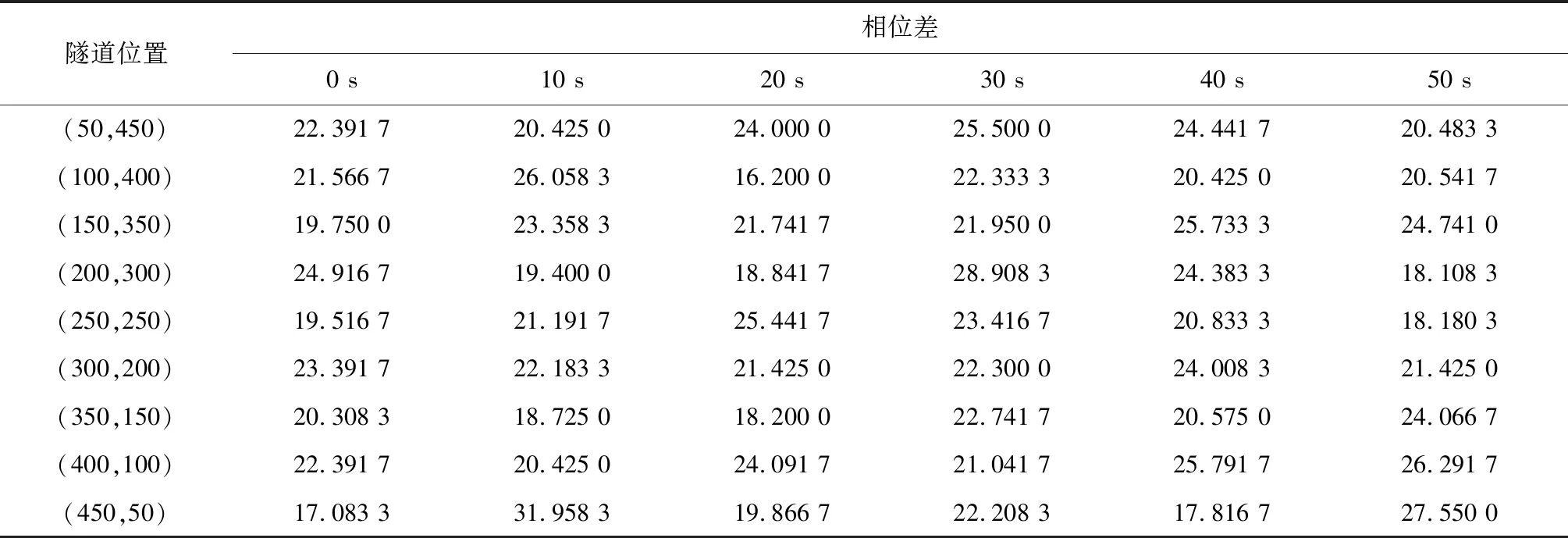
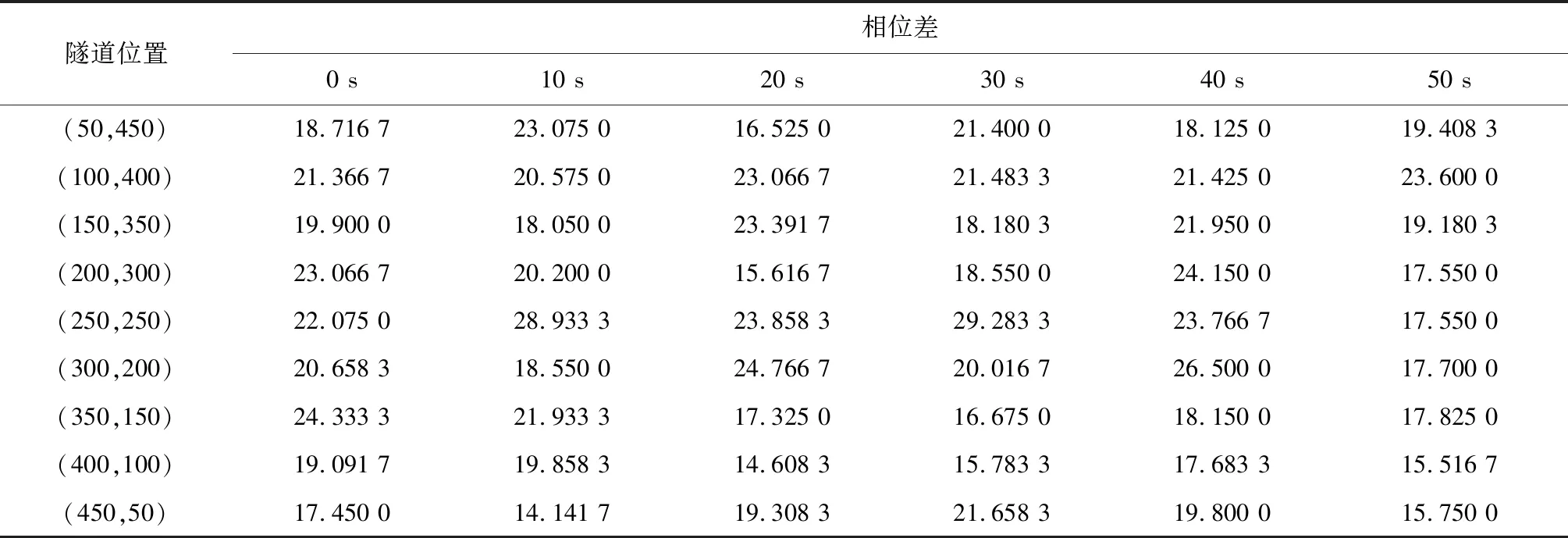
位置条件：当车辆处于信号灯前，即xn

(1)如果车辆前面的信号灯为红灯，那么vn→min(vn,dn,sn)；其中，sn为车辆到信号灯之间的空元胞数。

(2)如果车辆前面的信号灯为绿灯，在交叉口后面紧邻的两个元胞都被车辆占据，vn→min(vn,dn,sn)，否则vn→min(vn,dn)。

位置条件：当车辆通过信号灯或者在隧道中时，即xn≥Lsig2或者Lsig2

此时vn→min(vn,dn)。

Step4：随机慢化

由于道路上各种要素的影响及驾驶员的个人原因，车辆会随机减速。

道路上的车辆以概率pr进行随机慢化，vn→max(vn-a′,0)，a′表示车辆减速度；隧道内的车辆以ptr的概率进行慢化，其中ptr>pr，隧道内影响车辆速度的要素更多。

Step5：位置更新

xn→xn+vn。

本模型采用周期性的边界条件，车辆在离开道路尾端后重新进入道路，每组仿真时道路上的车辆数量保持不变。

3 数值模拟及仿真结果分析

3.1 仿真参数设置

根据常见标准车辆特性和实际道路特征，对实际参数进行了相应的修改，使其符合元胞自动机模型要求。仿真时取单个元胞长度1 m，车辆长度为7 m，道路限速72 km/h，隧道限速54 km/h；道路总长度为2000 m，交叉口之间的距离为1000 m，隧道长度为500 m；车辆加速度与减速度取a=a′=4 m/s2；信号灯的周期为60 s，其中绿灯时间40 s，红灯时间20 s；道路上随机慢化概率pr=0.2，隧道内随机慢化概率ptr=0.3，车辆换道概率pc=0.3。仿真时长13 600 s，取10 001 s到13 600 s为有效仿真时间，消除暂态的影响。

3.2 路段时空图分析

分别对低密度、中密度下隧道位置不同的城市路段进行仿真，仿真过程中，隧道设置于路段中间。如图2所示的是路段车流密度分别为0.05 veh/m和0.1 veh/m时，路段上车辆的时空云斑图。

图2 时空云斑图Fig.2 Spatiotemporal patterns

由图2a、c、e中可以看出，在小密度下，隧道入口越靠近上游交叉口，隧道的减速作用使得刚通过交叉口的车辆无法以较大车速行驶，形成减速波，影响到上游交叉口的车辆起动与车队疏散，导致上游交叉口的排队长度越大；而当隧道靠近下游交叉口时，由于隧道中的车流密度相对较大，下游交叉口出现红灯时，停止波传递到隧道中，使得隧道中出现车辆排队现象。而在图2b、d、f中，车辆出现较严重的拥堵现象，当隧道靠近下游交叉口时，隧道中的拥堵越严重；在图2b中，交叉口2的下游也出现了一定的拥堵，这主要是在周期性的边界条件之下，交叉口1的停车波向上传递所导致的；对于图2f，隧道出口离下游交叉口仅50 m，随着车辆位置的时空图形成了层次明晰的堵塞带，车辆的滞留造成了通行能力的降低。

3.3 基本图分析

分别对信号控制下的隧道路段(隧道位于路段中间，出入口离上下游交叉口各250 m)、普通路段以及无信号控制下的隧道路段与普通路段进行数值仿真，分析其速度-密度和流量-密度基本图。

车流密度k、平均速度v、流量q由以下公式得出：

其中，n为道路上的车辆数，N为路段长度，ΔT为统计时长，t0为统计开始时间，vi,t为t时刻第i辆车的速度。

得到速度-密度、流量-密度关系如图3所示。信号控制下的隧道路段的通行速度及通行能力要低于无信号控制的路段；自由流下，信号控制下的隧道路段通行速度较低主要是因为隧道限速低于路段限速且隧道内的随机慢化概率更高，信号灯周期性间隔作用也会降低车辆的通行速度；在拥堵流区域，各情形下速度-密度曲线以及流量-密度曲线区域基本一致，这是由于拥堵状态下车辆间的相互作用较大，车辆处于较低速度行驶，受隧道限速以及信号灯的影响较小；信号灯控制下的普通路段以及隧道路段的图像基本吻合，主要是因为信号灯的作用明显而隧道与普通路段上的限速差较小，对车辆的降速作用不明显，并且，隧道离上下游交叉口较远，起动波、停止波的传递与加速波、减速波之间的影响较小。

图3 密度图Fig.3 Density chart

3.4 信号灯相位差及隧道进出口位置设置对交通流影响

在城市路段中，隧道出入口与交叉口之间的相对位置不同也会影响车辆运行，需要不同的交通管控手段。本节将以不同的出入口位置及两信号灯相位差的组合研究交通流运行情况，探究城市隧道路段及交叉口通行能力。中密度(k=0.1 veh/m)下不同相位差下隧道处于不同位置时交叉口间路段通行能力及交叉口1、2的平均排队长度如表1～3所示。

表1 不同相位差不同隧道位置路段通行能力

注：表中隧道位置(a，b)，a表示隧道入口距离上游交叉口的距离Lin，单位m；b表示隧道出口距离下游交叉口的距离Lout，单位m。

表2 不同相位差不同隧道位置交叉口1排队长度

注：表中隧道位置(a，b)，a表示隧道入口距离上游交叉口的距离Lin，单位m；b表示隧道出口距离下游交叉口的距离Lout，单位m。

表3 不同相位差不同隧道位置交叉口2排队长度

注：表中隧道位置(a，b)，a表示隧道入口距离上游交叉口的距离Lin，单位m；b表示隧道出口距离下游交叉口的距离Lout，单位m。

表1所示的交叉口间路段通行能力，普遍处于0.65 veh/s(2340 veh/h)以上，在合适的信号配时组合下，通行能力可以得到一定的提升；然而当隧道出口离下游交叉口较近时，通行能力明显下降，且无法通过配时达到明显提升。表2、3则是上下游交叉口的排队状况，上游交叉口与下游交叉口在同样的信号配时下堵塞程度并不相关，一般来说，上游交叉口排队长度越长，下游交叉口排队长度越短，路段通行能力越强。

根据表1～3中数据，可以得出以下结论：

(1)对于城市隧道路段，在不同的配时下其通行能力也有所改变，合理的配时可以有效提高路段和交叉口的通行能力，减小交叉口的排队长度；表中隧道入口离上游交叉口200 m、信号灯相位差20 s时，两交叉口的平均排队长度均达到了最小值；

(2)在表格的最后一行，隧道离下游交叉口仅50 m时，无论在何种配时情况之下，其通行能力均处于比较低的状态，这主要是由于隧道出口与下游交叉口距离较短，隧道车辆原本就处于低速行驶状态，停车波传递到了隧道内，使得隧道内出现拥堵，降低了路段通行能力；

(3)对于表中第一行，隧道离上游交叉口较近，路段的通行能力相对较低，但并不明显，通过合理的配时可以提高路段的通行能力，使路段处于一个相对平稳的运行状态。

4 结论

本文建立了城市隧道路段的元胞自动机模型，通过数值仿真研究城市隧道路段交通流与隧道位置、信号灯相位差等之间的关系，发现城市隧道会降低路段和上下游交叉口的通行能力，合理的配时可以提升路段的通行能力，减小交叉口的排队长度；但是当隧道位置离下游交叉口较近时，路段通行能力明显降低，信号控制对通行能力的提升收效甚微，需要寻求更好的交通管理手段。本研究中，只考虑了单一路段上的交通流行驶对通行能力的影响，没有考虑横向路段的车流干扰，需要进行更加深入的研究。