找准基本教研点 做我们能做的事
姚志富
(安徽省芜湖市第十二中学 241003)
一、中学课堂教学是基本教研点的一片沃土,我们要深耕细作
对来自课堂教学这些教研点的研究,不仅可以丰富我们的教学内容、方法、技巧、思想从而极大地开阔我们的教学视野,还有可能帮助我们从教学人变成教育人.
1.课例的分析和点评
(1)好课的评价标准
①要看教学目标实现度,即必须实现这节课的教学目标,这要从目标的确定和教学各环节的实施效果两方面评价.
②要看教材的处理,即在教学过程中是否能够准确理解教材,驾驭教材,创造性地使用教材.我们主要从知识传授是否准确、把握重难度、突出重点、突破难点的过程和方法是否合理,以及对教材内容的调整是否科学,是否合理选择了教学方法.
③要看教学环节的设计与实施.主要看教学思路的设计是否符合教学内容的要求,是否符合学生实际情况,还要看教学思路是否层次分明、脉络清析,看各环节衔接是否严谨、自然并符合逻辑规律和学生认知规律.
④要看教学方法与手段.主要看方法和手段是否符合教学目标、教学内容的要求,看是否符合学生的身心发展要求和认知特点,看是否充分利用现有的教学手段来辅助教学.
⑤看教师基本功.主要看板书、教态、语言,即教师出手相是否好,语言功底对数学教师很重要,简炼重要,精炼及重要.
(2)有效的教学方法
①要根据教学内容而定.起始课、概念课就不太适合启发式的教学方法和合作、讨论式的教学方法,讲授法更适宜,而复习课就不太适宜讲授法,对内容熟悉的又有一定的方法基础,课堂教学要让学生动起来,在动的过程中发现问题、解决问题、总结提炼问题.
②要根据学生自身的特点.主要是指学生认知水平和思维水平,合作也好,议论也罢,不能走形式,要让学生能走进活动中去,否则就是一场戏.
③要根据教师自身的特点.每个教师都有自己喜欢的教学方法,古板严谨的教师有的是,尤其是数学教师,这也未必就是坏事,有些教学法我们很多人是玩不动、玩不转的,但是偶尔为之是必要的,否则学生是不喜欢你的,也会丧失兴趣的.
2.教材解读
这是我们更进一步理解、掌握并驾驭教材的有效途径,也是很基础的教研点.教材解读有很多种方式,但必须把握的应当有以下几方面:
(1)明确教学内容的课程目标和学习目标,以及这些内容对前后知识的贯穿作用,教学主线是什么,选择什么样的教学方法来实现课程目标和学习目标.
(2)教材内容的具体研读
包括章头图和引言的解读,对具体的概念、定义、公式、定理、推论以及例习题,练习题如何处理得要认真推敲打磨,这些方面主要是依据教材和教学大纲,结合个人的理解,但是我们能明显地感受到不同的教师会有不同的眼界和思维层次.
(3)对教学的建议
教材内容是“死”的,但是如何消化教材,如何运用教材,不同的教师会有不同的想法和做法,教学建议就显得很重要,这不仅体现出自己的认识水平,更是给别人的中恳建议和素材.这是教材解读有特色显个性的地方,建议可以从本章、本节内容的知识结构,重难点的合理定位,开拓创新地突破难点,鼓励学生探究性学习等几方面考虑.
3.解题方法及其解题教学的研究
包括具体数学问题的多途径解决及思考,解题思想和方法的研究以及高考复习过程中复习方法及相关问题的研究,数学竞赛问题的研究,这类问题归结起来就是提出问题,分析问题和解决问题,在尝试一题多题、命题意图分析、问题源分析的基础上,上升为思想方法的分析和指导,直至达到以一个问题解决一类问题的目的.这一基本教研点入口较宽,可以从一个小问题开始,尝试一题多解,一题多变再上升到一类问题解决方法的概括和总结.

解法一(函数法)x+y=5,∴0 解法三(三角函数法)令x=5sin2θ,y=5cos2θ. 这应当是奥赛教练员和爱好竞赛题研究的数学教师可以做的事,像安振平教授对不等式的研究不仅成果颇丰而且成果显著,像安师大郭要红教授对不等式和初等平面几何的研究也是成绩斐然,在这方面青年教师可以大胆尝试,相信会有大回报 这是一个永恒的话题,因为不会解题的老师绝对不是一个好老师,只会解题而不会一题多解、一题多变、融会贯通的老师同样不是一位好老师,在这个领域我们可以大有作为,可以从两方面入手: (1)是解题思维起点的合理性研究,即你是怎么想到的,为什么这么想,这对提高学生合理应用知识和方法有帮助. (2)是对解题过程中思维受阻从思维的合理性进行分析,努力找出原因并力争沿着原来的思维路线在优化思维方法的前提下解决问题. (《在数学案例分析过程中逐步成长》——《数学通讯》2014.4) (1)数学文化没有作为数学教育不可或缺的重要组成部分,给大家的感觉是数学没有历史,没有历史传承与阶段发展史,呈现给大家的仅仅是数学成果,这既与教科书编排没有很好地融入历史观、价值观有关,也与教育者急功近利的思想有关. (2)课堂数学中对数学文化价值的教育活动内容很单薄,零碎而不成体系,有些内容在章头图中,有的内容在“探究与发现”、“阅读与思考”等阅读材料中,让师生感觉可有可无,存在感不突出. (3)当前的高考中将数学文化列入考试内容之一,进一步弱化了数学文化价值的教育活动,如2015年全国课标1卷文科数学第(6)题,以文言文与白话文两种形式呈现,那文言文以及古代的这个数学问题存在又有什么必要呢?不是徒有其表吗?以这样的形式呈现又能说明数学文化什么样的价值呢?数学文化教育的意义又在哪里? (1)树立正确的数学史观.数学史的内容是非常丰富的,数学史是历史,它有过程,有思想方法,有正确的理论,也有疑问和谬误.我们在日常教学中可以挖掘数学相关理论及思想方法推演及演化过程、发展规律,对某些领域代表性的数学家可以研究其思维方式和方法.这对我们来说是一个启示,对某些问题的研究可以少走弯路,很方便地寻找到正确的解决问题的方法.因此在日常教学中,我们对某些问题研究时可以剖析数学家研究的曲折经历,思维方式和研究方法,让学生在这一过程既有情感共鸣,也有与数学家共同研究的实践经历. 例如人教A版选修1-1中“为什么截口是椭圆”这个问题 . (2)让学生感受到数学史就是一部创造史.学习数学史,是让我们感受到数学家“再创造”的思维过程,体会到数学史与其他历史一样,是一部社会发展的创造史,是以推动社会发展为根本目的.如引进负数是社会发展的需要,引进复数是为解决有关数学问题服务的,是为健全数系服务的.因此我们理解有关数学概念,要有“形”还要跳出“形”,最后融合社会需要这个根本,即数学是人类文化的重要组成部分,在推动社会进步和发展的过程中起着重要的作用.






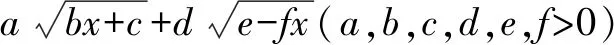
4.关于高中数学竞赛题的研究
5.关于中学解题教学的研究
二、开展对课标的研究,让我们站得更高,看得更远
1.当今关于数学文化价值的教育现状
2.如何有效开展数学文化价值的教育

