基于K-Means算法和重心法求解多配送中心选址问题

许彦宸，戴 韬

（东华大学，上海 200051）

1 引言

随着国民经济的快速发展以及网络的普及，越来越多的人习惯并且喜欢在网上购物，网上购物及一些O2O 服务的核心要素是其背后的配送体系，其中配送中心（配送站）的选址是一个影响最终响应速度的核心基础问题。由于我国幅员辽阔、客户需求井喷式涌现，无论是全国范围的全国性配送问题还是一个城市内的区域性配送问题，都面临着海量需求点的基本挑战，而现有的物流选址模型及算法往往只能求解十几个到几十个需求点的基础问题。因此，提出一种求解海量需求的多配送中心选址算法有非常强的理论与现实意义。

2 文献综述

多设施选址问题一般可以转化为P-中值问题，该问题是由Hakimi 在1964年所提出，具体是指在已知需求点位置、待建中心的数量以及待选点位置集合的情况下，为P 个中心找到合适的位置，并为每个需求点指定一个中心，使得所有需求点到各自对应的中心点的总加权成本最低[11]。对于P-中值问题，学术界有多种求解方法和不同的思路，例如：Hansen等采用变领域搜索算法求解该问题[1]，而变领域搜索算法是常用的求解优化问题的算法之一，而P-中值问题的目标就是优化总加权成本；Mladenovi 等利用元启发式算法求解P-中值问题[2]，Colmenar等采用高级贪婪随机自适应搜索方法来求解[3]，该方法可以对传统的贪婪算法进行改进以降低其陷入局部最优解的可能性；Griffith等利用选址问题中的空间属性，使用空间自相关性方法对P-中值问题进行求解[4]；Youkyung Won则采用广义细胞形成的方法求解大规模多目标P-中值问题[5]；Drezner 等采用改进的启发式算法求解平面P-中值问题[6]，取得了显著的效果；Stefanello等对容量受限的P-中值问题进行了求解[7]；Carrizosa 等在网格上利用平方和为指标对数据进行聚类以求解P-中值问题[8]；而王飞飞和林文则对利用改进的重心—因次分析法求解3PL 配送中心选址问题进行研究并将其与P-中值问题进行联系[9]；张彩庆和赵璐利用改进的P-中值模型对电网检修公司分部选址问题进行研究[10]等。

3 基本模型与算法局限性分析

P-中值模型的数学表达式如下：

上述表达式中各符号的含义如下：i为需求点的编号、j为待建物流中心的编号；D为每个物流网点的需求量（一般与该网点所辐射的辖区内的人口数量成正相关）；W为物流中心与物流网点之间的加权成本（由距离、时间等因素共同决定）；Y 为0/1 决策变量，取0 表示物流中心j 不为需求点i 提供服务，而取1则表示物流中心j为需求点i提供服务；X同样也为0/1决策变量，取0表示该点不建物流中心，取1则表示该点建物流中心。M为所有网点的集合，而N则为待建物流中心备选点的集合。

式（1）是P-中值问题的目标，即加权成本的最小化；式（2）是对物流中心和需求点的关系的约束，具体是指每一个需求网点必须属于一个物流中心且只能属于一个物流中心；式（3）是对待建物流中心的数量进行约束；式（4）是要求需求点必须能被其所属的物流中心辐射到；式（5）是指在当前的j 位置是否建立物流中心；式（6）是指物流中心和物流网点之间仅有两种关系，物流网点属于物流中心与物流网点不属于物流中心[11]。

显然，P-中值问题是一个NP-Hard问题[12]。而求解P-中值问题的传统方法是需要先经过考察，预先指定N个备选点（N＞P），随后使用贪心算法或启发式算法等方法求解。其缺点在于：第一，在指定N个备选点的过程中，可能会受到多个方面的影响（如决策专家的水平等），使得所选择的N个备选点与潜在的正确的P个中心点的位置相去甚远，后续的计算过程也只是徒劳无功。第二，求解P-中值问题的传统算法只能求解规模较小的问题，一般为100个需求点以下。而如果超过该规模，计算的精度和速度都会受到影响。

对于本文所要研究的问题（以下简称本问题）而言，传统的P-中值问题的解决方案无法在付出合理成本的情况下解决。理由是：本问题的规模远超传统的P-中值问题的解法所能解决的规模（从表1可以得知）；此外，本问题并没有指定P 的值，因此N 个备选点的位置也无法确定。如果要进行多次尝试，就要多次确定备选点，所要花费的计算成本是非常巨大的，甚至可能在有效时间内无法得到可行的满意解。

表1 本文的需求规模与其他文献的对比

4 算法设计

4.1 流程图

本文提出的K-Means分类算法与重心法结合的算法逻辑如图1所示。

图1 K-Means算法结合重心法的算法逻辑

4.2 算法的详细描述

重心法是求解设施选址问题中最简单的问题—单一设施选址问题的常用方法之一[17]，数学表达式如下：

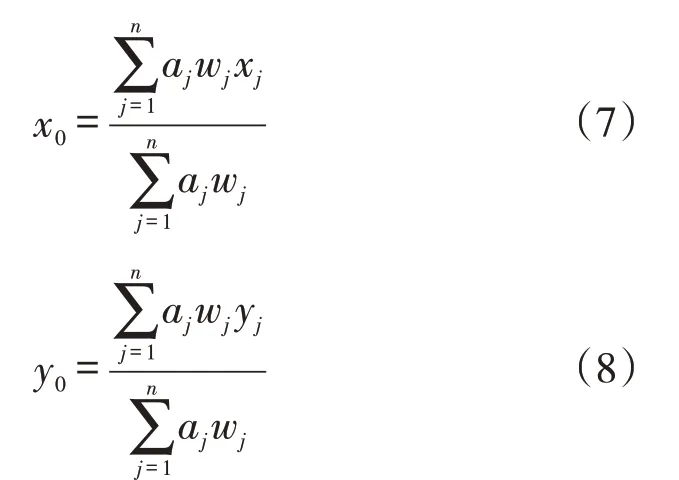
前文已经提及，本文所要解决的问题规模远超传统的P-中值问题的规模，因此需要一个新的方法，而聚类算法就是一个很好的选择。聚类算法的基本思想是将所给数据分为若干簇，使簇内的数据有较高的相似度，而簇间的数据则具有较大的差异性。K-Means算法是数据挖掘中的一种聚类算法，其具有算法思想简单、实现方便；算法的收敛速度较快以及能方便处理海量数据等优点。

基础K-Means算法的步骤如下：

步骤1：获取最大迭代次数Iter及数据集D；

步骤2：随机选择K个点为初始的簇中心；

步骤3：对于每个数据点，分别计算该点与K 个簇中心的距离,与该点距离最小（也称作相似度最大）的簇中心将是该点所属的簇;

步骤4：重新计算K 个簇的中心，中心为该簇内所有点的算术平均值；

步骤5：若迭代次数到达最大迭代次数或当前的簇中心集合与上一次迭代相比没有变化，则转到步骤6；反之则转到步骤3；

步骤6：输出数据集的分类结果（K 个簇中心的位置、每个点所属的簇以及簇内误差平方和等）。

可以注意到，K-Means算法在步骤2选择初始的簇中心集合时是随机进行的，这样会拥有非常快的速度并且该算法的实现非常简单，但是这样的结果是以精确率为代价换来的。因此，Arthur等便提出一种对选取K 个初始点的方式进行改进的K-Means 算法，被称为K-Means++[18]。另外，在Arthur 等的论文中，其中有些数据集的规模超过1 000。因此，本文使用K-Means算法改进算法是合理的。本文使用的改进算法主要针对基础算法的第2步，通过修改初始化K 个中心的方法改善了这个缺点，在减少迭代次数的同时并没有降低该算法的速度及其实现的简单性，其详细步骤描述如下：

步骤1：获取最大迭代次数Iter及数据集D。

步骤2.1：从数据集D 中随机选择一个点c1作为初始的第一个簇中心；

步骤2.2：选择下一个簇中心ci，而数据集中剩余的任意点x'，成为ci的概率是，其中 D（x）是指点x到已确定的聚类中心的距离；

步骤2.3：重复步骤2.2，直至有K 个初始中心被确定。

步骤 3 至步骤 6：与基础 K-Means 的步骤 3-6 相同。

从中可以看出，K-Means++与K-Means的区别仅仅在于步骤2（初始化K个中心的方法上）的不同，其余的步骤完全相同。因此，在实践过程中，仅需要将刚刚的K-Means算法中初始化的部分略作改动即可获得较大的速度方面的提升以及迭代次数的减少。另一点需要注意的则是，尽管在算法步骤5的原始描述的其中一个终止条件是本次迭代结束之后的簇中心集合与上一次迭代结束之后的簇中心集合相比没有变化，在实践的过程中往往利用公式来评判该次聚类的效果[13]，其中为第k个簇的中心，E则是簇内误差的平方和。在实践过程中，通常要求，其中δ是一个充分小的正数。

基于上述分析，本文的基本思路是先将所有的需求点划分为K 个簇，然后将每一簇视为单一设施选址问题利用重心法进行求解[3]。虽然，K-Means++算法的K 值也无法确定，但是可以利用循环结构解决传统的P-中值问题在每次运算之前都需要花大量计算时间去决策的备选点集合的确定问题，可以极大地减少最终的总时间。

根据现实配送管理问题的背景，我们需要让尽量多的需求点在约定的配送距离以内，因此提出以噪音率衡量最终的选址结果。具体是将与其所属的中心点之间的距离大于给定覆盖半径的需求点记为噪音点。

具体的数学表达式如下：

其中，式（9）用于计算每个需求点到其所属中心点的距离，其中k 表示第i 个需求点属于第k 类。而式（10）中Noise Rate的下标d则表示噪音率受到给定的配送中心覆盖半径d的影响。

5 算例实验

5.1 数据预处理

为求解上述问题并验证本文所提出方式的可行性，本文选用“数据超市”中公开的“百度地图POI-全国各城市快递网点数据”的示例数据[19]进行验证，共1 000条数据。尽管初始数据一共有16个特征，但是仅需要使用lat（纬度）和lng（经度）两个特征，在设施选址问题的领域内这种特征的选取方法也是较为常见的[20]。对经过处理的数据执行可视化操作，如图2所示。

图2 所有需求点的位置

从图2中可以看出，该样本的分布基本符合中国各地区的快递情况，因此这份数据是可信的。

5.2 实验结果分析

该算法在CPU为i5-8250U的笔记本电脑上运行的时间在330s 至350s 之间。因此，该方法可以在合理时间内解决大量需求点的选址问题。

仅考虑待建中心数量和噪音率的关系。在给定覆盖半径为120km 的条件下，绘制出结果图，如图3所示。从图3中可以看出，该算法最终是收敛的。但在某些情况下，随着物流中心的个数增加，噪音率同样也会有所波动，这是本文算法作为启发式算法的一个缺点。

为了保持问题的一般性，我们不假设任何与运营相关的效益与成本系数，因此仅以噪音率来刻画配送中心的收益。通过图3发现，在新建100个左右配送站点时，新建站点边际收益迅速下降，当配送站点数量超过175时，收益更是几乎没有任何增加。单从图上来看，100个左右的配送站点可能是较为可行的结果，若现实最终的数量在此范围附近时，需要逐一计算每个点的加权成本加以确定。

将覆盖半径也作为变量加入到考虑中来，绘制出的结果如图4所示。从图中可以发现，在任何变量的搭配下该方法都可以收敛，因此该方法是现实可行的。

6 总结

本文首先提出需求点数量巨大、配送中心数量未知的多配送中心选址问题，并指出传统的求解该类型问题的方法无法在有效时间内解决。因此本文提出一种基于K-Means算法和重心法结合的算法求解该问题，并提出使用K-Means++算法改进基础算法进行需求点的分类。由于一般的K-Means算法中的“距离平方和”指标并不能准确的反映配送问题的实际分类效果，因此，本文又提出了“噪音率”指标来刻画配送管理背景下需求点与配送中心的平均距离。最后，本文选用公开的数据集（共计1 000 个需求点）验证了算法的合理性。本文提出的分类结合重心法的方式为解决现实中海量需求的配送站点选择问题提供了一种新的思路。

图3 待建配送中心个数与噪音率的关系

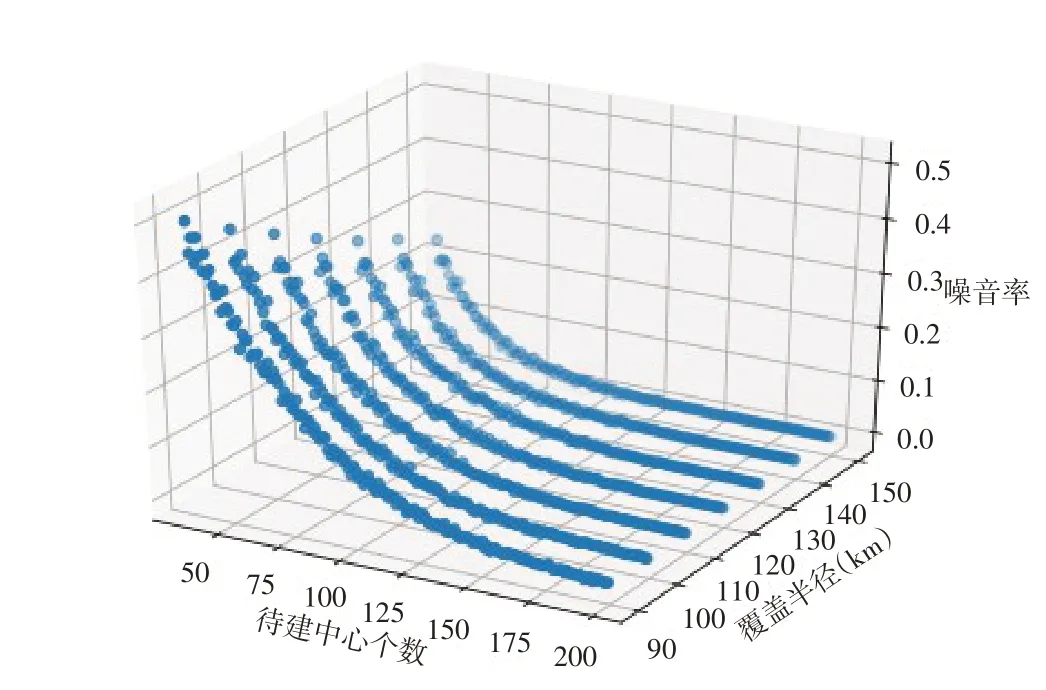
图4 待建中心个数、覆盖半径和噪音率之间的关系