高考巾算法经典问题聚焦
2019-06-26 12:45刘大鸣
中学生数理化·高一版 2019年1期
刘大鸣

算法是高考每年必考内容,大多以客观题形式出现,难度为中等偏下,考查方式多为程序框图或算法语句,按题型划分主要有求结果、填补过程、求输入变量这三类问题。这类问题常与函数、不等式、数列、概率与统计等知识交汇命题。
聚焦1:利用条件结构求分段函数的分界点
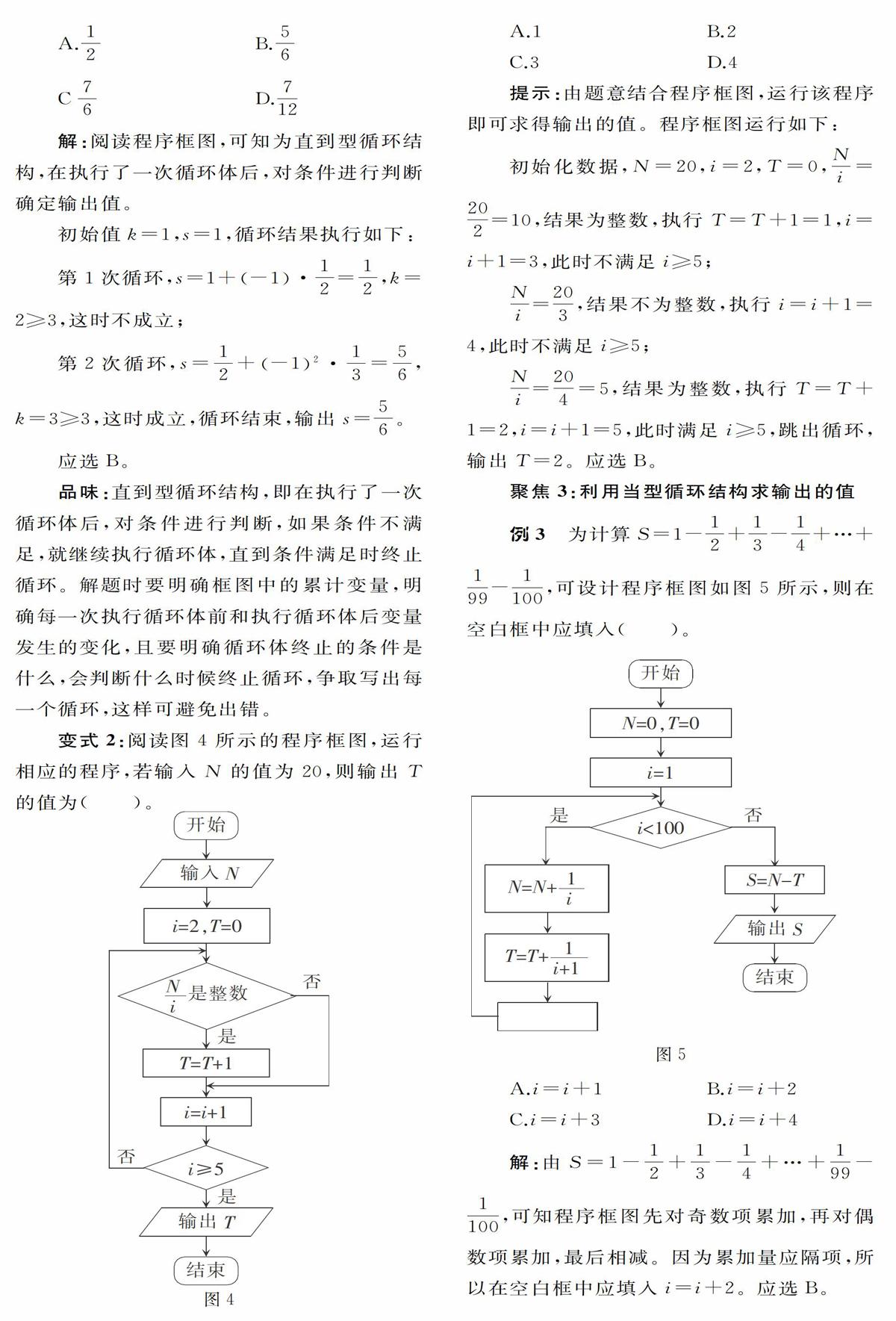
例1 执行如图l所示的程序框图,当输入x的值为4时,输出y的值为2,则判断框中的条件可能为()。
B.x>3
B.x>4
C.x≤4
D.x≤5
解:依據条件结构可知此算法的程序功能为分段函数寻求分界点。
当输入x的值为4时,输出y的值为2或6。由lOg2x=2,可知x=4不满足判断框内的条件,则只能是x>4。应选B。
品味:对于算法与程序框图,要明确算法框图中的顺序结构、条件结构和循环结构。条件结构的程序框图中的条件语句是表达选择结构最常用的语句。条件结构常与分段函数交汇,考查求函数值、值域、自变量的值或寻找分界点。
猜你喜欢
福建中学数学(2021年5期)2021-03-01
语数外学习·高中版中旬(2020年8期)2020-09-10
少儿美术(快乐历史地理)(2020年4期)2020-08-24
中学生数理化(高中版.高考数学)(2020年3期)2020-05-25
中学生数理化(高中版.高考数学)(2018年12期)2019-01-17
中学数学杂志(高中版)(2016年5期)2016-11-01
时代风采(2009年21期)2009-03-23

