基于随机稀疏阵列的滑坡MIMO雷达成像方法

杨中丽， 蒋留兵

(1.桂林电子科技大学 信息与通信学院,广西 桂林 541004；2.桂林电子科技大学 计算机与信息安全学院,广西 桂林 541004)

地基雷达由于受环境因素影响小、具备全天候监测能力，同时可以进行无接触式的监测，充分保证监测人员的安全，近年来用于监测山体滑坡成为人们研究的热点[1]。本研究主要针对山体滑坡监测的关键技术——地基雷达成像进行研究。现用于滑坡监测的典型的成像系统如LISA(linear SAR)[2]和GBInSAR(ground based InSAR)系统IBIS(image by interferometry survey)[3]，均是依靠天线在水平直轨道运动实现高的方位向分辨率。MIMO雷达利用其多发多收体制形成的虚拟天线阵元替代物理天线阵元[4]，可以很好地解决合成孔径的导轨运动控制精度和大孔径阵列的问题。然而由于雷达结构的特殊性，传统的成像算法，如距离多普勒算法和CS(chirp scaling)算法不再适用。王怀军等[5]基于MIMO雷达成像引入后向投影(back projection,简称BP)算法，并进行时延曲线校正，但其串行处理方式严重限制了成像算法的效率。王伟等[6]在标准BP算法和TCC-BP算法基础上，提出一种基于距离补偿和波束形成的改进MIMO雷达BP成像算法，提高了成像的运算效率，但需要的天线数目仍然较多。近年来，有不少学者把压缩感知理论引入MIMO雷达成像中，利用低维测量值获得重构的高质量图像。Gu等[7]在艇载雷达运动目标成像中利用压缩感知理论，实现了高质量的MIMO雷达二维成像，大幅降低了天线数目。HU等[8]结合窄带双基地MIMO雷达和压缩感知理论提出一种超分辨三维成像方法，解决了三维成像的低分辨率问题。因此，结合压缩感知理论的降维思想引入随机稀疏阵列模型，分时发射步进频信号并分时接收回波信号，对接收到的回波信号距离向采用逆傅里叶变换脉冲压缩，方位向利用等效随机稀疏阵列作为低维测量值，结合正交匹配追踪算法进行压缩处理，实现随机稀疏阵列的滑坡监测二维成像。

1 稀疏阵列MIMO雷达信号模型

传统MIMO雷达系统是由M发N收的均匀阵列组成，接收天线间隔为λ/2，发射天线间隔为N(λ/2)，λ为信号波长。这种布阵方式最大限度地利用了合成的等效虚拟阵列，在阵列孔径足够大的情况下，就能够实现方位向分辨率的要求。在实际成像中，阵元数过大会提高系统硬件成本和计算复杂度，为了解决阵元数过大引起的问题，采用稀疏阵列进行MIMO雷达成像。

MIMO雷达模型需要保证各信号通道的独立性，通常发射天线数要远小于接收天线数，所以对数目较多的接收天线进行稀疏布置：从N个均匀布置的接收天线中随机选取N′个，接收阵列稀疏比例定义为η=N′/N。

为保证阵列孔径长度足够大，第一个和最后一个接收天线位置不变，根据得到的N′个随机稀疏接收阵元和M个周期稀疏布置的发射阵元，利用多项式理论[9]得到MN′个虚拟阵元。以2发6收的阵列为例，MIMO稀疏布阵结构示意图如图1所示。

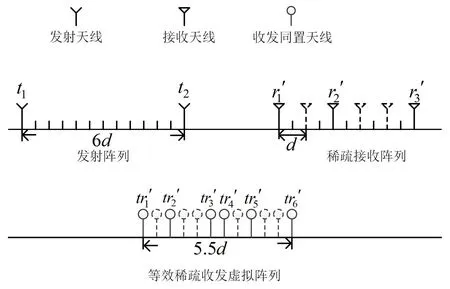
图1 MIMO稀疏布阵结构示意图

MIMO雷达采用上述稀疏天线布阵方式，雷达模型采用分时发射信号波形和分时接收回波信号的工作模式。步进频连续波技术[10]可获得高的距离向分辨率，所以发射信号选取步进频连续波，设发射信号中单个脉冲表示为S(t)，如式(1)，

S(t)=exp(j2π(f0+iΔf)t)rect(t-iTr),

i∈(0,1,,Q-1)。

(1)

其中：f0为脉冲起始频率；Δf为频率步进量；Tr为发射信号子脉冲时宽；Q为子脉冲个数。则第m个发射天线发射的步进频信号为Sm(t)，表达式为：

m∈(1,2,,M),

(2)

其中，Am为第m个发射信号的能量。

雷达信号由M个发射阵列分时发射到监测区域后，回波信号被N′个接收天线分时接收，因此形成了MN′个观测通道。假设第m个发射阵元发射的回波信号被第n′个随机稀疏接收阵元接收，将该观测通道回波信号幅度放大并经过解调采样后为：

i∈(0,1,,Q-1),

(3)

(4)

其中：δ为目标散射系数；τmn′为第mn′个观测通道的时延；(x0,y0)、(xn′,0)、(xm,0)分别为目标和收、发天线的坐标；c为光速。

2 基于稀疏阵列的MIMO雷达成像方法

2.1 逆傅里叶变换实现雷达数据距离向压缩

采用的分时发射和分时接收的方式，在雷达完成一次监测区域照射时已经把各通道的数据分离出来，但是距离向数据还没有被压缩处理。步进频连续波是一个频域信号，变换到时域可以形成一个sinc函数信号，sinc函数实际就是一个窄脉冲，根据窄脉冲出现的不同位置，可以得到斜距不同的目标，从而在距离向分离出不同位置的目标。

根据第1节所述，雷达系统对监测区域完成一次照射后，得到一个原始雷达数据矩阵I[MN′,Q]，Emn′,i为矩阵I第mn′行i列的元素，表示为：

Emn′,i=Amn′δexp(j2πf0(-τmn′))·

exp(j2πiΔf(-τmn′))。

(5)

在小间距布阵情况下，MIMO雷达等效收发阵列的长度远小于目标到各个阵元的距离，距离徙动不明显，因此，距离向只需要进行IFFT变换[10]即可得到较为准确的压缩数据。对矩阵I[MN′,Q]按行分别进行IFFT，得到第mn′行数据为：

sinc(πB(tk-τmn′))

(6)

2.2 基于时延补偿因子稀疏基的压缩感知方位向压缩

(7)

其中观测矩阵Φ={φu,v}为广义单位阵，且

φu,v=

(8)

Φ矩阵由MN′行MN列元素构成，δu由等效稀疏收发天线位置决定，且矩阵的每行只有第δu个元素为1，剩下的全赋值为0。

对应地，原始均匀阵列得到的回波数据Y可由稀疏变换矩阵变换为

Yq=ΨΘq。

(9)

其中：Θq为第q个距离单元的目标散射点信息；Ψ为稀疏变换矩阵。

雷达监测区域距离向从ymin到ymax，方位向从-x到x，根据滑坡监测区域的几何形状，得出监测区域波达角的覆盖范围为(-arctan(x/ymin),arctan(x/ymin))，将其均分为MN份，得

l∈(0,1,,MN-1)，

(10)

令Wl,mn=exp(-j2πf0sinθl(xm+xn)/c)，可由Wl,mn组建MN行MN列时延补偿因子矩阵如式(11)：

(11)

时延补偿因子与信号本身在某种程度上存在一一对应的关系，很全面地反应了散射点的特征信息，故可把其作为稀疏变换的稀疏基进行后续的数据压缩处理。

在构造稀疏接收阵列时，接收天线是随机选取的，等效的虚拟收发阵元的位置也是随机的，满足广义单位阵Φ与Ψ不相干的要求，因此Φ·Ψ满足RIP(restricted isometry property)条件[11]。由以上构造的稀疏变换矩阵和观测矩阵，利用正交匹配追踪算法[12]对X的第q行求解以下问题：

(12)

然后对所有的q=1,2,,Q求解式(12)问题，即可得到二维像。

3 仿真实验

为了验证算法的正确性进行数值仿真实验。雷达发射步进频信号，载频15 GHz,带宽300 MHz,子脉冲数4096个。这里按照稀疏布阵方法布置6发25收的阵列，均匀接收阵元的间隔为λ/2，发射阵元的间隔为50×(λ/2)，阵列稀疏度为50%。根据山体滑坡的实际成像场景设置雷达仿真参数。雷达成像区域为距离向从1000～2000 m,方位向为-150～150 m。点目标的散射系数都设为1，附加噪声为加性高斯白噪声，信噪比为10 dB。

首先分析单点目标成像，目标方位向为0 m，距离向为1500 m，图2给出了文献[6]方法和本算法成像结果。从图2看出，2种方法均对单点聚焦正确成像，但是图2(a)的旁瓣值明显，图2(b)没有这种情况，且图2(a)的分辨率低于图2(b)。表明对于单点目标成像，本方法成像效果明显优于文献[6]方法，且对于单点目标成像没有伪影点出现。

其次，图3分析了多点目标成像,目标点位置信息为：tg1-(0,1500)，tg2-(-25,1505)，tg3-(25,1505)，tg4-(0,1510)。仿真结果如图3。图3(b)中由于阵元的缺失，不能很好处理欠采样数据，呈现出的7个点目标图像模糊，只能大致辨别几个目标点的不同位置信息，且旁瓣水平比单点目标成像恶化明显。图3(c)表明了本方法在稀疏阵列下多点目标聚焦成像的效果优于文献[6]。

为了更加清晰地对比本方法的成像效果，图4分别给出了本方法和文献[6]方法方位向为-25的切面图和距离向为1500的切面图。从图4(a)可明显看出，方法的方位向分辨率高于文献[6]方法，且旁瓣值水平比文献[6]方法好，表明本方法能利用较少的测量值获得较高的方位向分辨率。图4(b)显示的2种方法的距离向分辨率的值相同，这是因为距离向分辨率由发射信号带宽决定的。

图2 单点目标稀疏阵列成像对比

图3 多点目标稀疏阵列成像对比

图4 目标距离向和方位向切面图对比

4 结束语

目前山体滑坡雷达由于导轨式作用机理，使其设备成本高，不利于市场推广。在保持雷达高分辨率的前提下，以降低设备复杂度和成本为目的，结合压缩感知理论，引入了随机稀疏收发阵列，对地基MIMO雷达稀疏成像进行初步研究，提出一种距离向逆傅里叶变换和方位向正交匹配追踪的成像方法。结合滑坡雷达实际场景参数，通过数值仿真对比得出本方法能够利用较少的测量值获得较高分辨率的二维雷达图像。