非剪胀土体中土钉室内拉拔有限元模拟

刘川川，张捷，吴鸣

（汕头大学 土木与环境工程系，广东汕头 515063）

0 引言

室内拉拔试验是很多研究者研究土钉拉拔特性和土钉抗拔承载力时采用的重要手段[1-3]。土钉室内拉拔试验的有限元模拟可对室内试验结果进行验证并深入探究各因素对土钉抗拔承载力的影响。目前，与土钉室内拉拔有限元模拟有关的研究还相对较少。其中Su[4]对土钉在非饱和全风化花岗岩土体的室内拉拔试验进行了有限元模拟，分析了土钉上覆压力和剪切带土体的剪胀角对拉拔破坏界面极限剪应力的影响；Zhou[5]对土钉在饱和全风化花岗岩土体中室内拉拔试验的整个的钻孔、注浆、遇水饱和、拉拔过程进行了有限元模拟。Su[4]和Zhou[5]所模拟土体都是较为密实的土体并且土体剪胀性较强，然而，很少有研究者对非剪胀土体中土钉的室内拉拔试验进行有限元模拟。通常较大围压的松散土体其剪胀性基本可以忽略，可视作非剪胀土体。从现代土力学概念出发，土体内摩擦角可视作由临界内摩擦角和剪胀角两部分组成[6]。土体剪胀角受各种外界因素影响较大，难以精确确定，而临界内摩擦角可视为土体的固有参数。非剪胀土体其内摩擦角φ'与临界内摩擦角φ'c近似相等，变量更为单一，因此从非剪胀性土体出发更易初步探究土钉的拉拔机理，加上很多计算土钉抗拔承载力的经验公式都是基于忽略土体的剪胀性建立的，因此可采用非剪胀性土体中土钉拉拔有限元模拟以对土钉拉拔机理进行探究并对经验公式进行验证。为此本文对Prandhan[7]所建立的松散土体中土钉的室内拉拔试验进行了有限元模拟。本次模拟考虑到对表面粗糙的注浆土钉，拉拔破坏来自于周围土体的剪切破坏而不是钉-土之间的界面滑移，故本次有限元模拟在钉-土之间建立薄层单元模拟钉-土之间的剪切带，进而模拟土钉拉拔过程中土体的剪切破坏。

本文共采用两种有限元模拟方式，一种是考虑钻孔过程的模拟方式，一种是不考虑钻孔过程的模拟方式。最终将两种模拟方式下的模拟结果与Prandhan[7]试验结果进行对比，判定模拟方式的有效性。确定有效的模拟方式后，本文采用其中有效的模拟方式分析了内摩擦角对模拟结果的影响，并利用模拟结果评价了两种普遍采用的计算土钉抗拔承载力的经验公式的合理性。

1 有限元模型的建立

1.1 有限元模型参数确定

此次有限元模拟网格划分在Hypermesh软件中进行，而模型的求解在Abaqus中进行。土钉的密度，泊松比参考Su[4]、Zhou[5]的取值为2e-9t/mm3，0.28， 因模拟的Prandhan[7]室内试验土钉与Su和Zhou所采用土钉具有较大相似性，因此土钉密度和泊松比的参考取值具有合理性。模拟土钉的弹性模量基于钢筋部分和混凝土部分的截面面积进行加权平均，即

式中：Eeq为土钉的弹性模量；Es为构成土钉的金属杆体的弹性模量；Eg为构成土钉的水泥浆体的弹性模量；As为构成土钉的金属杆体的横截面积；Ag为构成土钉的水泥浆体的横截面积。

本次模拟中，根据文献[8]，Es、Eg分别取为200GPa、13.5GPa；构成土钉的金属杆体直径为25mm，土钉的直径为100mm，据此计算出AS、Ag，带入式（1）计算出Eeq=25.2GPa。

在Abaqus中，进行初始地应力平衡时，土体的静止侧压力系数是基于泊松比进行计算的，即

保证有限元模型中静止侧压力系数与正常固结土体静止侧压力系数公式计算结果一致，泊松比满足如下条件

式（2）、（3）中：K0为土体的静止侧压力系数；υ为土体的泊松比；φ'c为土体的临界内摩擦角。

Prandhan[7]室内试验中土体的临界内摩擦角为φ'c=39O，因此按式（3）计算有限元模型中泊松比为υ=0.27。

土体的干密度为ρd=1428kg/m3，土体天然含水量为w=9%，因此有限元模拟中取模拟土体的密度为ρ=ρd(1+w)=1615.4kg/m3。

最终有限元模拟中所有的物理力学参数如表1所示。

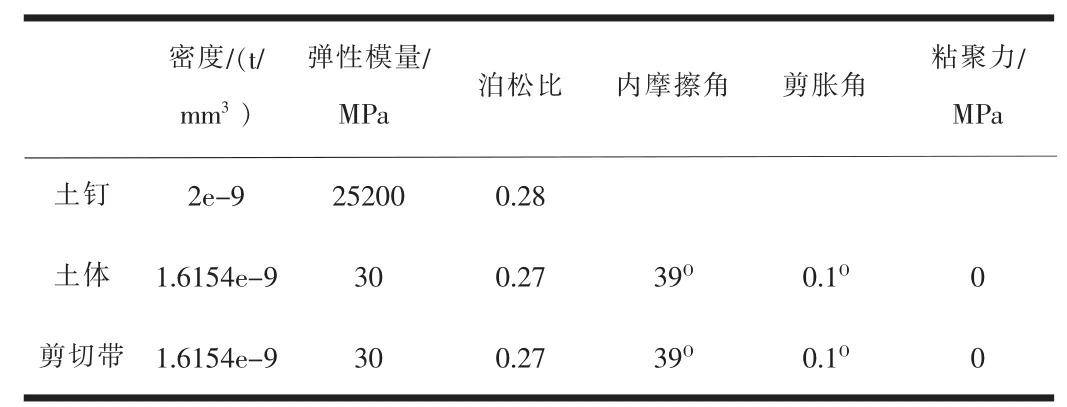
表1 有限元模拟中的物理参数

1.2 有限元模型建立

Prandhan[7]的室内拉拔试验箱尺寸为长×宽×高=2m×1.6m×1.4m，假定土钉安装高度为0.7m，安装位置为宽×高所在截面的中心位置。

图1 单元划分后的有限元模型

本次有限元模拟对土体和土钉皆采用C3D8R单元，土钉单元与剪切带土体单元之间以及剪切带土体单元与外围土体单元之间都采用Tie的方式进行绑定。单元划分完成 后的有限元模型如图1所示。

Prandhan[7]进行了不同上覆压力下土钉的拉拔试验，本文选 取 其 中 上 覆 压 力 分 别 为 17.05kPa、34.43kPa、66.15kPa、94.26kPa、107.03kPa下共5组室内拉拔试验进行有限元模拟。

室内拉拔试验中土钉的上覆压力主要包括两部分，第一部分是土钉上覆土体的自重应力，第二部分是通过液压千斤顶传至模型箱顶面的压力。上覆土体的自重应力可在地应力平衡阶段施加。在本次进行的5组有限元模拟中，土钉的上覆土体自重应力均为1615.4×9.8×10-3×0.7=11.08 kN/m2。 有限元模拟中通过向模型土体顶面施加均布荷载的方式来模拟液压千斤顶传递的压力。从土钉所受的上覆压力中去除来自上覆土体的自重应力，则在5组有限元模型中施加于模型土体顶 面 的 压 力 分 别 为 5.97kPa、23.35kPa、55.07kPa、83.18kPa、95.95kPa。

本次有限元模拟共采用了两种模拟方式。第一种模拟方式考虑土钉安装中的钻孔过程，第二种模拟方式不考虑钻孔过程。

（1）考虑钻孔过程的土钉拉拔有限元模拟需在两个独立相同的模型中得以完成。

模型1中第一步对包括土钉、剪切带土体和外围土体单元在内的有限元模型进行自动地应力平衡，此处进行平衡的地应力包括土钉上覆土体的自重应力和来自模型顶面的压力；第二步利用生死单元的方式移除构成土钉的单元来模拟钻孔过程，并将剪切带土体和外围土体单元的应力导出。

模型2中第一步导入来自模型1的单元应力，第二步进行与模型1同样的地应力平衡和土钉单元移除，第三步通过生死单元的方式恢复土钉单元并通过对土钉钉头施加位移的方式模拟土钉的拉拔。

（2）不考虑钻孔过程的有限元模拟所有模拟步骤在一个模型中即可完成。第一步对包括土钉、剪切带土体和外围土体进行自动地应力平衡；第二步通过对土钉钉头施加位移的方式模拟土钉的拉拔。

如图，在整个模拟过程中，为与实际边界条件一致，在进行地应力平衡时对土体模型底面施加Z方向的位移约束，对土体模型两个侧面施加Y方向的位移约束，对土体模型的正面（与土钉长度方向垂直的面）和反面施加X方向的位移约束，同时对土钉的钉头与钉尾施加X方向的位移限制。在进行土钉拉拔时，解除对土钉钉头与钉尾X方向的位移限制，并对钉头施加X方向正向的位移。

本次模拟中剪切带土体在厚度方向共设一层单元，为探究剪切带厚度对模拟结果的影响，本次有限元模拟分别模拟剪切带土体单元厚度为4mm和8mm的情况，并对结果进行了比较。这里剪切带厚度的选择分别借鉴Su[4]和Zhou[5]在土钉室内拉拔有限元模拟中对剪切带厚度的选定，其中Su[4]选定为4mm，Zhou[5]选定为8mm。

2 模拟结果分析

2.1 考虑钻孔过程与不考虑钻孔过程的模拟结果

选用剪切带厚度为4mm的有限元模型，考虑钻孔过程与不考虑钻孔过程的两种模拟方式下的拉拔曲线分别如图2、图3所示。

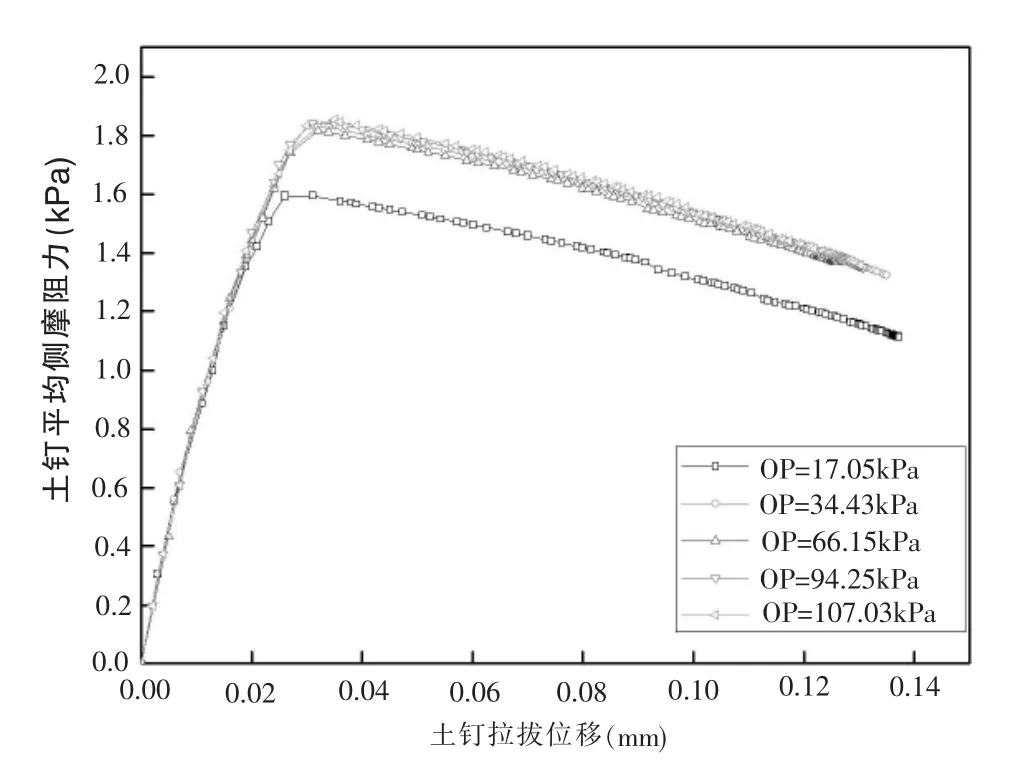
图2 考虑钻孔的模拟方式下不同上覆压力下的拉拔曲线

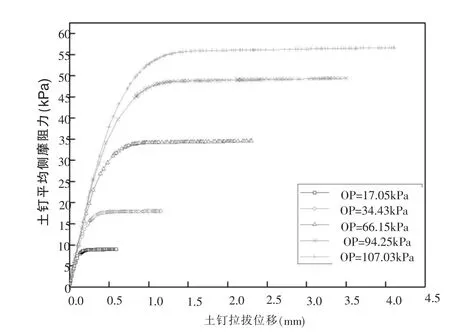
图3 不考虑钻孔的模拟方式下不同上覆压力下的拉拔曲线

将两种模拟方式下得到的土钉极限平均侧摩阻力结果与Prandhan[7]室内试验结果进行对比，对比结果如图4所示。

图4 两种模拟方式下的模拟结果与室内试验结果对比

从图4可以发现，当上覆压力较小时，不考虑钻孔的模拟方式下土钉平均侧摩阻力明显小于室内拉拔试验结果；而当上覆压力大于34.43kPa时，不考虑钻孔的模拟方式下的有限元模拟结果与室内试验结果非常接近。这是因为当上覆压力较小时，即使是松散土体也会表现出很强的剪胀性，而本次有限元模拟完全忽略土体剪胀性。但对上覆压力较大情况下的松散土体，土体剪胀性很小，可基本忽略，所以高围压下不考虑钻孔的有限元模拟方式可得到与室内拉拔试验一致的结果。

另外，从图可发现考虑钻孔的模拟方式下得到的土钉平均侧摩阻力始终远小于室内拉拔试验结果，因此可说明考虑钻孔过程的有限元模拟方式对非剪胀性土体中室内拉拔试验无法进行很好的模拟。这一现象与Su[4]，Zhou[5]在剪胀性土体中有限元模拟结果恰好相反，这是因为在剪胀性土体中，土钉拉拔过程中土体因剪胀受到外围土体约束时应力可得到一定的恢复，但在非剪胀性土体中却难以实现。

2.2 不同剪切带厚度下的模拟结果

剪切带厚度为4mm与8mm时土钉的拉拔曲线对比如图5所示。

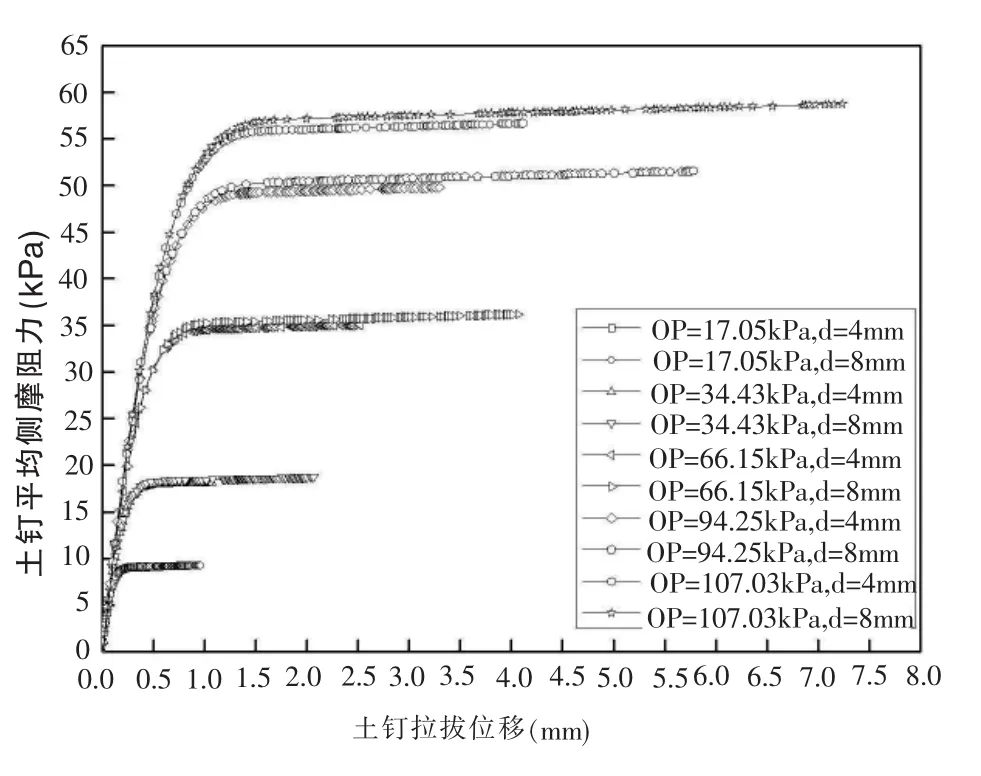
图5 剪切带厚度为4mm与8mm下土钉拉拔曲线对比

从图5图可以发现，同等上覆压力下剪切带厚度为4mm与8mm的土钉拉拔曲线基本重合，而对应的土钉平均侧摩阻力也基本一致，因此剪切带厚度的差异基本不会对模拟结果造成影响。

3 土钉抗拔承载力公式验证

当不考虑土体剪胀时，用于土钉抗拔承载力计算和用于土钉拉拔试验数据回归分析的常见表达式主要有两种，如式（4）、（5）所示。

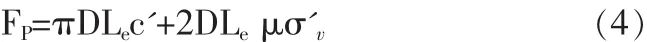
式中：FP为土钉的抗拔承载力；D为土钉直径；Le为土钉有效锚固长度；c'为土体粘聚力；σ'v为土钉上覆压力；μ为拉拔破坏界面摩擦系数。

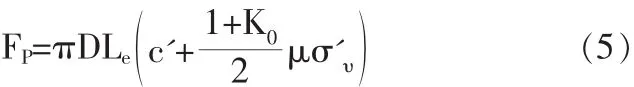
式中：FP为土钉的抗拔承载力；D为土钉直径；Le为土钉有效锚固长度；c'为土体粘聚力；K0为土体静止侧压力系数，取K0=1-sinφ'c；σ'v为土钉上覆压力；μ为拉拔破坏界面摩擦系数。

式（4）、（5）的理论差别主要体现在对作用于土钉表面法向应力的表达式。式（4）中仅考虑竖向应力σ'v的作用，式（5）中的土钉表面法向应力则是基于对土钉周围应力分析得到。

现通过室内拉拔有限元模型对两种计算表达式的合理性进行评价。一般情况下土体的临界内摩擦角范围为33°～40°[5]，因此分别选择临界摩擦角为33°、36°、39°的情况进行有限元模拟来验证两种表达式的合理性。本次有限元模拟假定拉拔破坏面发生在土钉周围剪切带土体，因此对式（4）、（5）中的μ取μ=tanφ'c。表2对有限元模拟得到的土钉极限平均侧摩阻力和式（4）、（5）得到的计算结果进行了对比。

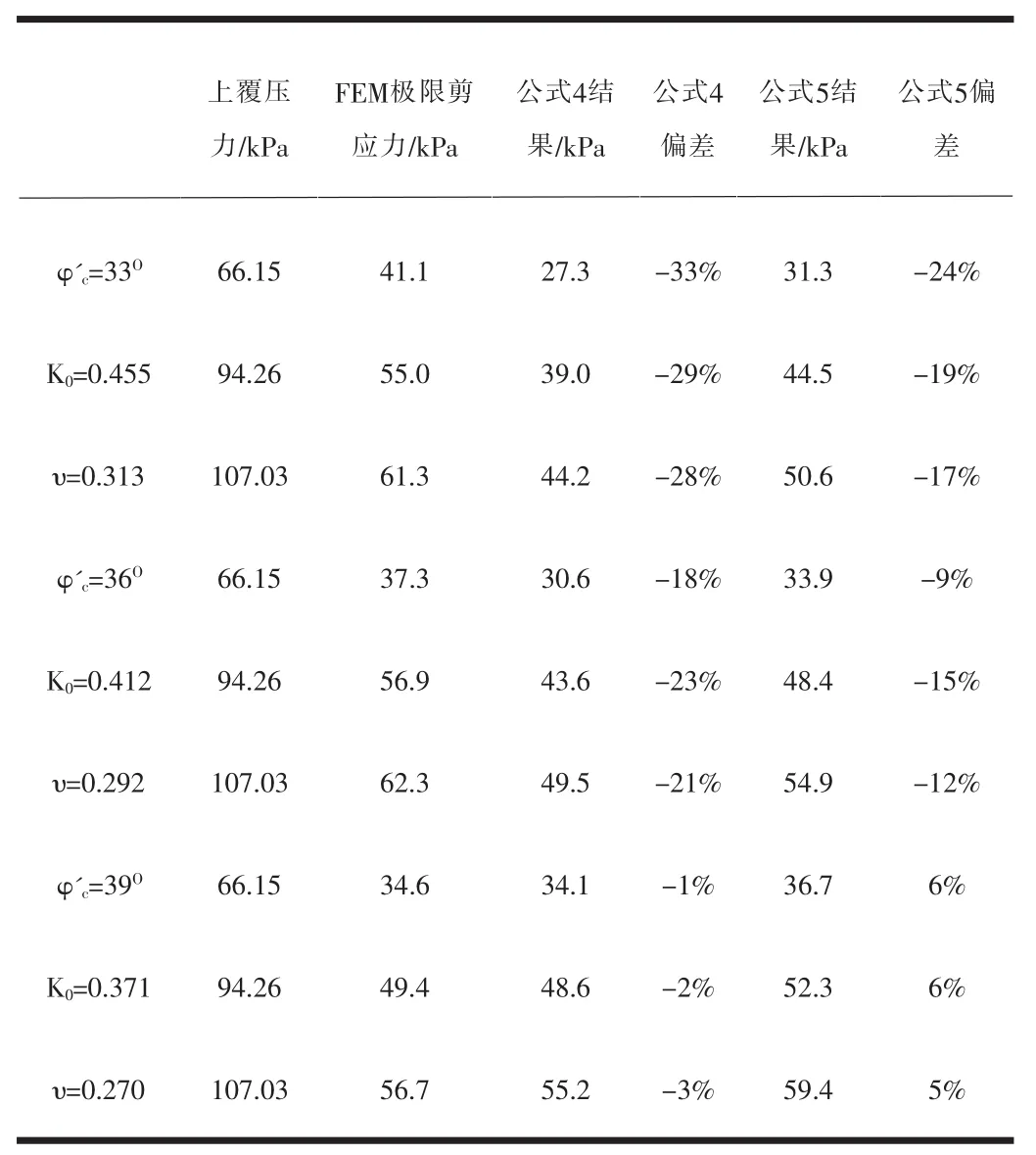
表2 有限元模拟结果与式（4）、（5）计算结果对比

通过表2可以发现，在一般的临界内摩擦角范围内，多数情况下采用式（5）计算的土钉极限平均侧摩阻力与有限元模拟结果更为接近，而式（4）则产生的偏差较大。

4 结语

（1）分别采用考虑钻孔的有限元模拟方式与不考虑钻孔的有限元模拟方式模拟了松散土体中土钉的室内拉拔过程，结果表明对非剪胀性土体（高围压下的松散土体）不考虑钻孔的模拟方式得到的土钉极限平均侧摩阻力与室内试验结果较为接近，考虑钻孔的模拟方式与室内拉拔试验结果偏离较大，因此不考虑钻孔的模拟方式更适用于模拟对非剪胀性土体中土钉的室内拉拔过程。

（2）当采用薄层单元模拟剪切带土体进而模拟土钉拉拔过程时，4mm薄层单元厚度与8mm薄层单元厚度模拟得到的土钉拉拔曲线接近，因此有限元模拟中薄层剪切单元的厚度差异对模拟结果基本不会造成影响。