压电驱动微动平台结构的设计优化和仿真分析
李东明,柴长忠,沈文强,王彦琪,崔云先
(大连交通大学 机械工程学院,辽宁 大连 116028)
0 引言
压电驱动的柔性铰链微动平台因响应快,结构紧凑,分辨率高等优点而被广泛使用,如微机电系统(MEMS)的加工制造,细胞注射,原子力学显微镜(AFM)精度的提高等,均占有极其重要的地位[1]。近年来,Mikio Muraoka等利用位移放大机构设计的二维精密定位平台,定位精度可达10 nm,行程可达400 μm[2];南洋理工大学[3]设计了一种三向大行程操作平台,其具有较大的刚度,各向定位精度在20 nm内;朱军辉设计的刚度为2.21 N/μm二维纳米定位平台,其固有频率为556.02 Hz、559.42 Hz,重复定位精度为±33 nm[4];上海交通大学设计了一种新型的垂直运动精密微定位平台,行程可达112.9 μm,刚度为3.167 N/μm,固有频率为636 Hz[5];南京航空航天大学提出的新型二维压电工作台x、y向刚度分别为4.923 N/μm、5.931 N/μm,两方向行程分别为41.6 μm、42.9 μm,其位移分辨率为50 nm[6]。由此可见,驱动位移和刚度是相互矛盾的物理量,人们希望在满足位移要求时,获得尽量大的刚度和高的定位精度。
本文设计了一种双平行柔性铰链结构的二维微动平台,在满足不低于5 μm的位移条件下,获得了刚度高于5 N/μm的微动平台。对其进行仿真分析表明,微动平台具有良好的静、动态特性。
1 二维微动平台的结构设计
设计的二维微动平台结构如图1所示。平台整体布局采用串联式结构,以双平行柔性铰链结构作传动机构,柔性铰链为双圆弧形,平台可实现在输出位移方向直线运动,无附加位移,输出结果精确。平台由压电陶瓷执行器驱动,其定位精确,分辨率高;x向压电陶瓷驱动平台做左右运动,y向压电陶瓷驱动平台做上下运动,且x、y向的柔性铰链布置方向垂直,平台x向运动时,y向柔性铰链结构相对为刚性结构,反之亦然,即x、y向运动位移无耦合。

图1 二维微动平台结构示意图
2 微动平台结构优化
为了平台能获得更好的静、动态特性,需要对平台作主要传动机构的双平行柔性铰链结构进行结构优化,使平台在给定位移的情况下,刚度达到最大,定位精度和固有频率最高。
2.1 设计变量的确定
根据图1所示的结构可知,本文使用的是半圆弧柔性铰链,其刚度主要由半径r、厚度t决定。由于采用双平行柔性铰链结构作为传动机构,因此,选取r、t和同侧两柔性铰链半圆弧圆心距l作为设计变量,即X=[x1,x2,x3]T=[r,t,l]T。
2.2 目标函数的建立
2.2.1x(y)向刚度
因x、y向结构一致,故两个方向的刚度也一致,只需要计算一个方向的刚度即可。图2为双平行柔性铰链结构的等效力学模型,图3为单个双圆弧柔性铰链模型。
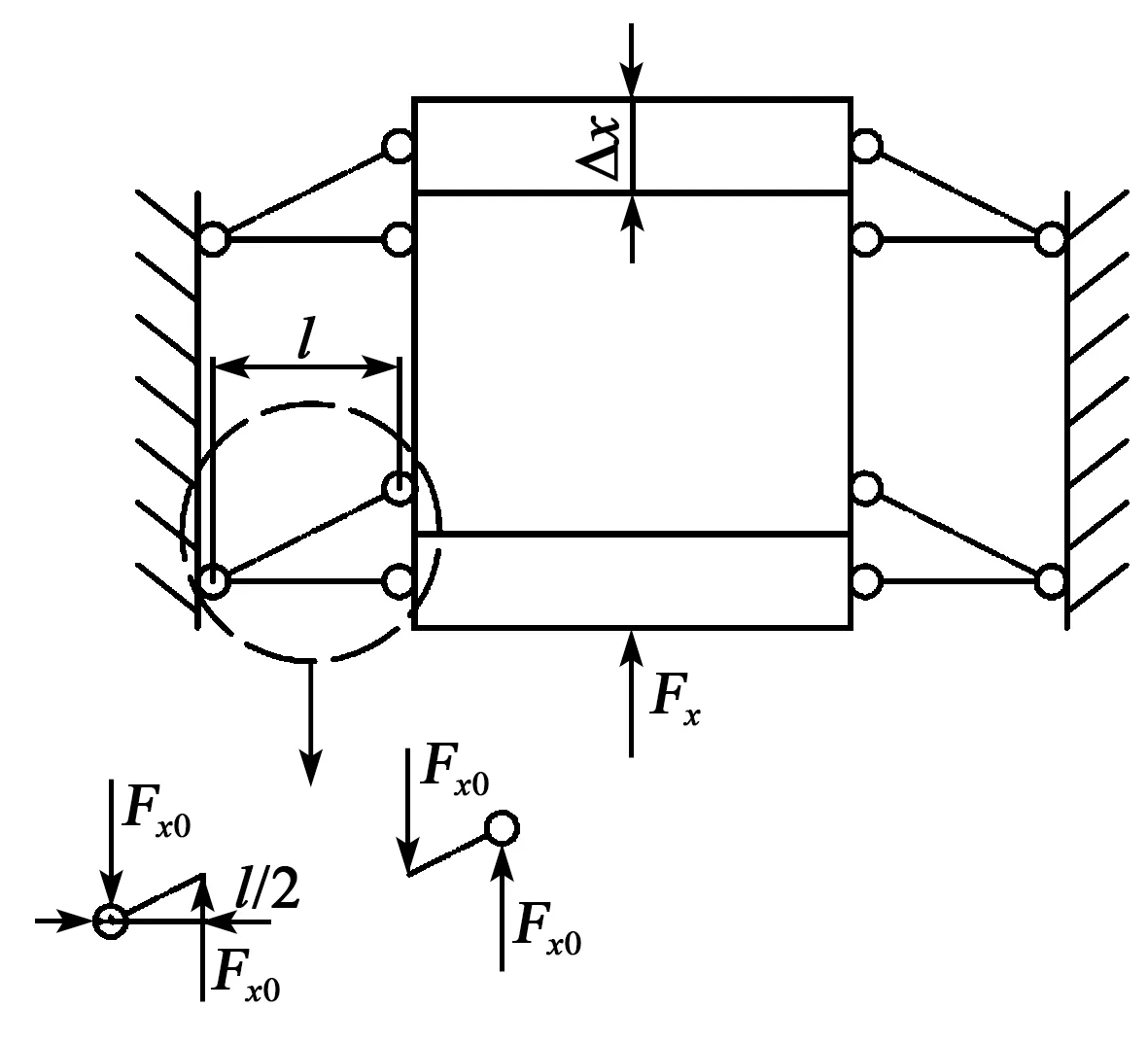
图2 双平行柔性铰链结构等效力学模型
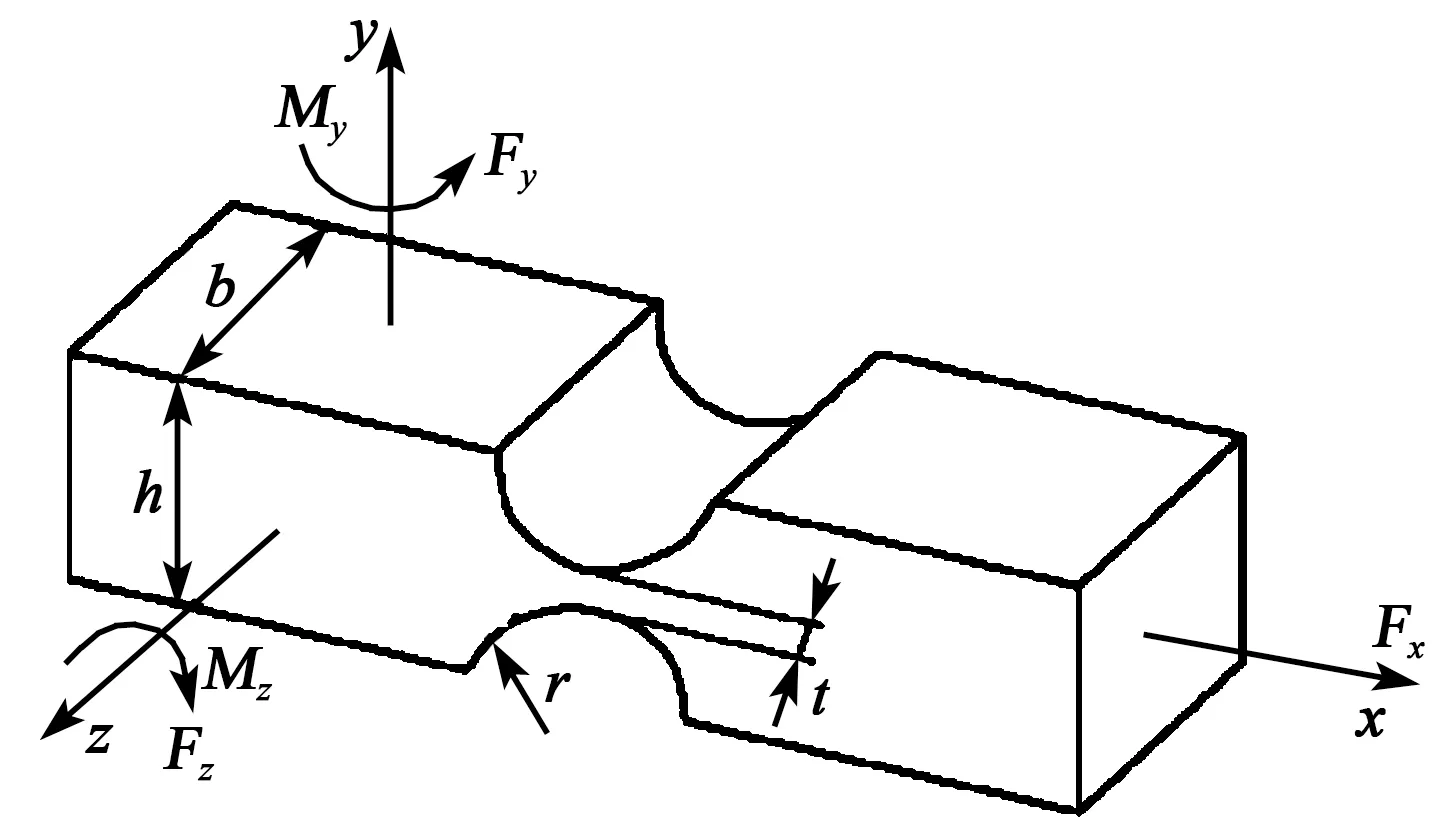
图3 单个双圆弧柔性铰链模型
根据功能原理可知,运动过程中微动平台所积蓄的弹性势能为
(1)
式中:Fx为平台所受的驱动力;Δx为平台的输出位移;Kα为图3中柔性铰链绕z轴的转角刚度;α为柔性铰链绕z轴的转角。
图3中,在绕z向弯矩Mz作用下,根据单轴双圆弧柔性铰链的理论计算式[7]可知:
(2)
式中:E=196.5×109Pa为所用材料的弹性模量,本文所用材料为65Mn;b为柔性铰链z向的长度。
因此,平台x(y)方向的刚度Kx理论计算式为
(3)
2.2.2z向刚度
微动平台在z向刚度的计算方法与x向一致。图3中,在绕y向弯矩My作用下,根据单轴双圆弧柔性铰链的理论计算式[8]可知:
(4)
(5)
式中:Kβ为图3中柔性铰链绕y轴的转角刚度;s=r/t。因此,平台z向刚度为
(6)
2.2.3 平台结构优化多目标函数的建立
在给定的位移条件下,本文要求各方向上刚度最大,此为多目标优化问题。本文采用线性加权法建立综合考虑平台各方向刚度的统一目标函数,因为x(y)方向和z方向刚度同等重要,因此,两个方向的权重值(w1,w2)都取为1,即w1=w2=1。本文目标函数为
(7)
2.3 约束条件的建立
2.3.1x(y)向最大位移至少5 μm
本文要求x(y)向的最大位移Δx≥5 μm,根据选用的压电陶瓷驱动器可得平台所受最大驱动力Fmax=264 N。由此可得
(8)
2.3.2z向最大位移不超过1 μm
本文要求微动平台在Fz=70 N的作用力下z向位移不超过1 μm,即
(9)
2.3.3x(y)向最大应力不超过许用应力
(10)
2.3.4z向最大应力不超过许用应力
微动平台在z向的最大应力计算和x向一样,得出z向最大应力σ2应满足如下条件:
(11)
2.3.5 保持双平行柔性铰链结构形状基本不变
为保证优化后的双柔性铰链结构的形状不发生较大的变化,根据初始值,应满足如下要求:
4r-l≤0
(12)
2.4 平台多目标结构优化的求解
本文以x(y)和z向的结构刚度为优化目标,是多目标优化问题,同时又有约束条件,也是一个有约束非线性规划问题。由于序列二次规划算法在求解有约束非线性规划问题中具有收敛性好,计算效率高,边界搜索能力强的优点,因此,本文采用该算法对平台结构优化数学模型进行求解。
在MATLAB软件中已含有基于序列二次规划算法的优化求解程序,即在MATLAB软件中调用fmincon优化程序便可对有约束非线性规划问题进行求解。因此,使用初始值和上述统一目标函数以及约束条件,在MATLAB软件中进行编程,对结构优化的数学模型进行求解。求解后的微动平台柔性铰链的r、t、l分别为1.01 mm、0.34 mm、4.05 mm。根据优化后的数据可计算出平台刚度的理论值:平台x(y)方向刚度理论值Kx=5.46 N/μm,位移理论值Δx=6.89 μm,z向刚度理论值Kz=70 N/μm。
3 微动平台的有限元仿真
3.1 平台静态性能仿真
本文采用ANSYS软件本身的三维建模模块对平台进行三维建模,并进行静态仿真。对平台进行自动网格划分,划分后平台有878 113个网格单元和1 323 634个节点,对平台添加固定约束和驱动力,而后求解平台的最大输出位移和应力云图。图4、5分别为平台x、y向的仿真应力云图。

图4 平台x向应力云图

图5 平台y向应力云图
由图4、5可知,两方向的最大应力均远小于材料的许用应力,满足应力约束条件。由仿真结果可知,x向位移为7.01 μm,y向位移为6.76 μm,x向刚度为5.36 N/μm,y向刚度为5.56 N/μm,均满足要求。对比位移理论值Δx=6.89 μm、刚度理论值Kx=5.46 N/μm,x向位移误差为1.7%,y向位移误差为1.9%,x、y向刚度误差均为1.8%。根据误差大小可知优化结果可靠。
Solar cycle modulation on the relationship between North Atlantic Oscillation and Middle East subtropical
误差产生的原因主要有:
1)理论计算忽略了铰链的伸缩变形。
2)理论计算忽略了材料变形带来的反作用力。
3)理论计算的简化力学模型与仿真模型有差异。
4)仿真中网格划分的精密程度影响仿真结果。
5)仿真计算求解存在一定的近似计算。
3.2 平台动态性能分析
对上述建立的三维模型进行前6阶的模态仿真,即在分析树处添加要求解的前6阶总变形命令,而后进行求解。观看仿真后的模态振型图,其仿真振型图如图6所示。

图6 微动平台模态振型图
由图6可知,平台x向固有频率为1.363 kHz,y向固有频率为1.027 kHz,两者均大于1 kHz,具有良好的动态特性。
4 结论
1)本文采用双平行柔性铰链结构设计了一种二维串联式微动平台,并用二次序列规划算法对其进行了结构优化,优化结果为:r=1.01 mm,t=0.34 mm,l=4.05 mm。
2)微动平台x(y)向位移理论值为6.89 μm、刚度理论值Kx=5.46 N/μm,满足x(y)向刚度高于5 N/μm,位移不小于5 μm的设计要求。对平台进行动、静态仿真分析,x、y向位移结果分别为7.01 mm、6.76 μm,x、y向刚度分别为5.36 N/μm、5.56 N/μm。与位移理论值相比,x、y向位移误差分别为1.7%、1.9%;与刚度理论值相比,x、y向刚度误差为1.8%,表明优化结果可靠。
3)根据模态分析可知,x、y向固有频率分别为1.363 kHz、1.027 kHz,均大于1 kHz,即微动平台具有良好的抗震性和动态特性。

