四音叉定子驱动的压电旋转电机动力学特性

贺红林，余 九，龙玉繁，付 磊，刘浩康

(南昌航空大学 航空制造工程学院，江西 南昌 330063)

0 引言

压电电机是基于逆压电原理、振动原理、摩擦理论，利用定子推动动子产生旋转运动或直线运动[1-3]。根据其不同的驱动原理，目前典型的旋转超声电机类型包括环形薄板行波类、杆式摇头类、不连续接触纵、扭复合类、不连续接触的弯振复合旋转超声电机。旋转超声电机具有转矩大、速度低，可直接驱动，响应迅速，位置分辨率高，无电磁干扰及运行时无噪声等优点，被广泛应用于航空航天、精密驱动、生物医学等领域。1993年，瑞士学者 G-A.Racine等制造了一种驻波驱动型旋转超声电机[4]，该电机尺寸为6 mm×6 mm×2 mm，在10 V的驱动电压下，无负载转速达600 r/min。1998年，日本新生公司的研究员K.Tani等研发了一种利用悬臂梁的伸缩和弯曲模态的新型结构旋转电机[5]，在驱动电压峰值为10 V 时，转速可达450 r/min。2002年，宾州大学研制出一种中空式结构的定子[6]，工作时转速为570 r/min，输出力矩达1.8 mN·m，电机的工作效率为25%。2002年，浙江大学研究出利用纵扭模态复合的旋转超声电机[7]，该电机的直径为80 mm、长110 mm。2006年，赵淳生院士团队基于Burhanettin Koc发明电机的基础上，提出了一种新型的金属管式电机[8-9]，工作频率为75 kHz，激励电源的幅值为60 V时，空载转速为813 r/min。2016年，纪跃波教授研制的多定子旋转超声波电机，在激励电压幅值为100 V、频率为3.75 kHz时，测得振动行波的幅值为1.76 μm，转速为97 r/min[10]。总体看来，现已推出的旋转超声电机型式有限，电机性能普遍不高。为丰富旋转电机型式，本文提出四音叉定子驱动的旋转电机。本文对电机的驱动机理、动力学优化、运行特性等进行了深入研究。

1 电机运动机理及结构设计

1.1 定子结构设计及工作模态选择

如图1所示，电机定子结构由四音叉结构组成，定子中心开设有通孔，用以通过旋转电机的旋转轴；通孔周围对称设置4个螺纹孔，用以将定子固定在支座上。选取定子的面内弯振和面外弯振作为电机的工作模态，电机耦合两相工作模态，实现绕z轴的旋转运动。

图1 定子结构及工作模态图

1.2 定子压电陶瓷激励配置

根据定子工作模态和振型，其压电极化及供电方式配置如图2所示。用正弦信号Usinωt激励面外弯振，余弦信号Ucosωt激励面内弯振，这使面内、面外弯振响应的相位差为90°。各陶瓷片均沿背离粘贴面方向极化，同时，各陶瓷片与定子基体粘结的电极均接地，以避免短路。为增强各工作模态的振动幅度，将各陶瓷片(PZT)尽量贴在弯振模态波峰(谷)处。

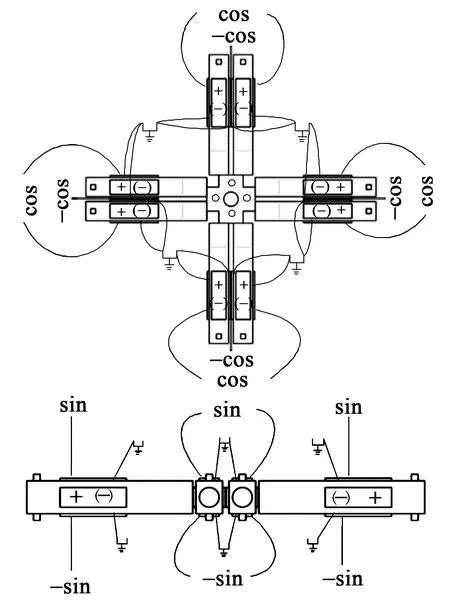
图2 定子上压电陶瓷极化(上)及其供电配置(下)

1.3 驱动足椭圆运动

取四音叉定子的一半驱动段作为研究对象，在该段定子上取杆端的质点A。当定子运动时，质点A的运动轨迹如图3所示。A点的位移可表示为

ux=Uxsin(ωt+φ)

(1)

uy=Uysin(ωt)

(2)

式中：ω为激振电压圆频率；φ为两相振动相位差；Ux,Uy分别为驱动足沿x、y向振幅，其值取决于激振电压。

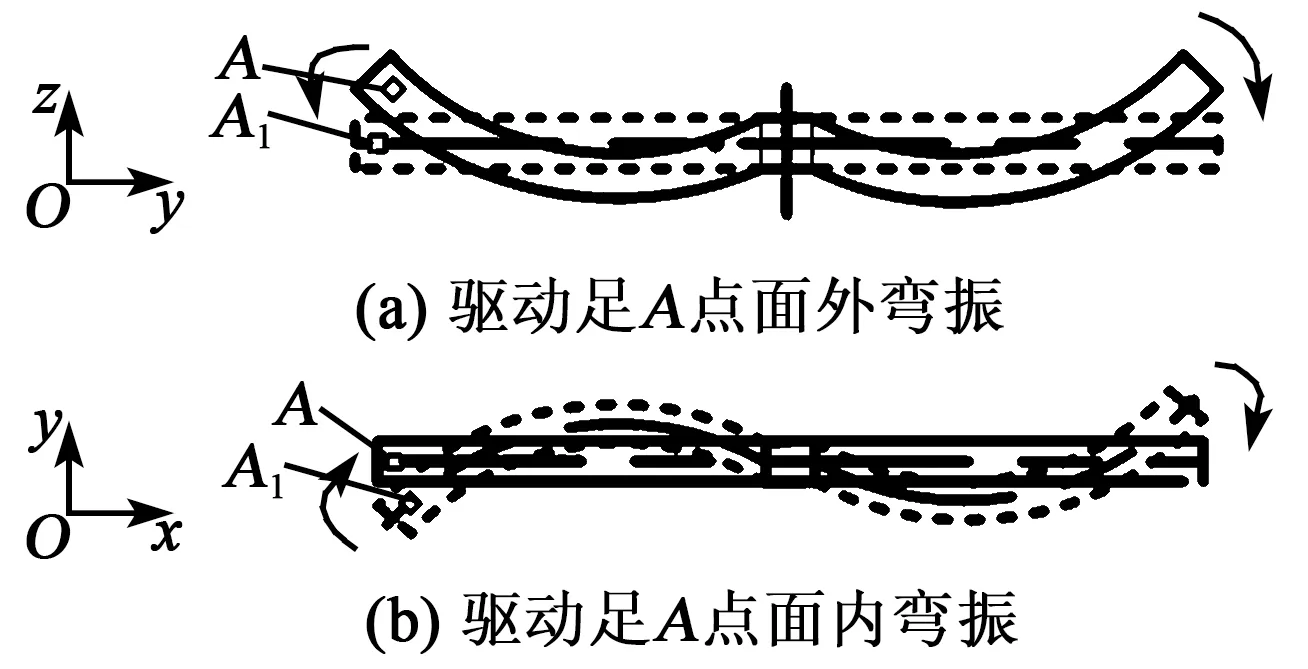
图3 驱动足A点运动轨迹

式(1)、(2)消除公共部分，得到

(3)

由式(3)可以看出，质点A的运动轨迹为形状变化的椭圆，椭圆的形状跟两相运动时间的差值相关。采用Matlab软件对式(3)进行模拟，确定φ值，得到质点A的运动轨迹(见图4)。由图可见，当φ∈[-π/2,0)时，驱动足做正向椭圆运动；当φ∈(π/2,π)时，驱动足做反向椭圆运动；仅当φ=π/2时，驱动足才形成最规则的椭圆轨迹。

图4 不同相位差下的运动轨迹

1.4 定子驱动原理

四音叉定子的旋转运动靠音叉杆面外弯振实现定子与动子的接触，靠面内的异对称弯振实现定子x、y方向的旋转。定子驱动原理如图5所示。将定子的一个振动周期T分为以下4个阶段，则相应的椭圆轨迹由4部分组成：

1)在0～T/4振动时段内，定子面外弯振使上下对称的音叉杆由直杆状成最大前弯状，其上部的驱动足与转子接触；此时，左右对称的音叉杆由直杆状成最大后弯状，且不与转子接触；定子面内弯振使上下对称的音叉杆由初始位置B1行至B2处。在该时段，上下对称的音叉杆上的驱动足同时推动转子产生沿x的正反方向的切向力，形成x方向绕中心轴的旋转力偶，推动转子形成x方向绕中心轴旋转的第一个步距。

2)在T/4～T/2振动时段内，定子面外弯振使上下对称的音叉杆由最大前弯状恢复成直杆状，其上部的驱动足与转子保持接触；此时，左右对称的音叉杆由最大后弯曲状恢复成直杆状，且其上部的驱动足与转子不接触；定子面内弯振使上下对称的音叉杆由B2处行至B3处，在该时段，上下对称的音叉杆上的驱动足同时推动转子产生沿x的正反方向的切向力，形成x方向绕中心轴的旋转力偶，推动转子形成x方向绕中心轴旋转的第二个步距。

3)在T/2～3T/4振动时段内，定子面外弯振使上下对称的音叉杆由直杆状弯成最大后弯状，其上部的驱动足与转子脱离；此时，左右对称的音叉杆由直杆状弯至最大前弯状，其上部的驱动足与转子接触；定子面内弯振使上下对称的音叉杆由B3处行至B4处，在该时段，左右对称的音叉杆上的驱动足与转子接触，推动转子产生沿y的正反方向的切向力，形成y方向绕中心轴的旋转力偶，推动转子形成y方向绕中心轴旋转的第三个步距。

4)在3T/4～T振动时段内，定子面外弯振驱使上下对称的音叉杆由最大后弯状恢复成直杆状，其上部驱动足与转子脱离；此时，左右对称的音叉杆由最大前弯状恢复成直杆状，且其上部的驱动足与转子接触；定子面内弯振使上下对称的音叉杆由B4处恢复至B1处；在该时段，左右对称的音叉杆上的驱动足与转子接触，推动转子产生沿y的正反方向的切向力，形成y方向绕中心轴的旋转力偶，推动转子形成y方向绕中心轴旋转的第四个步距。

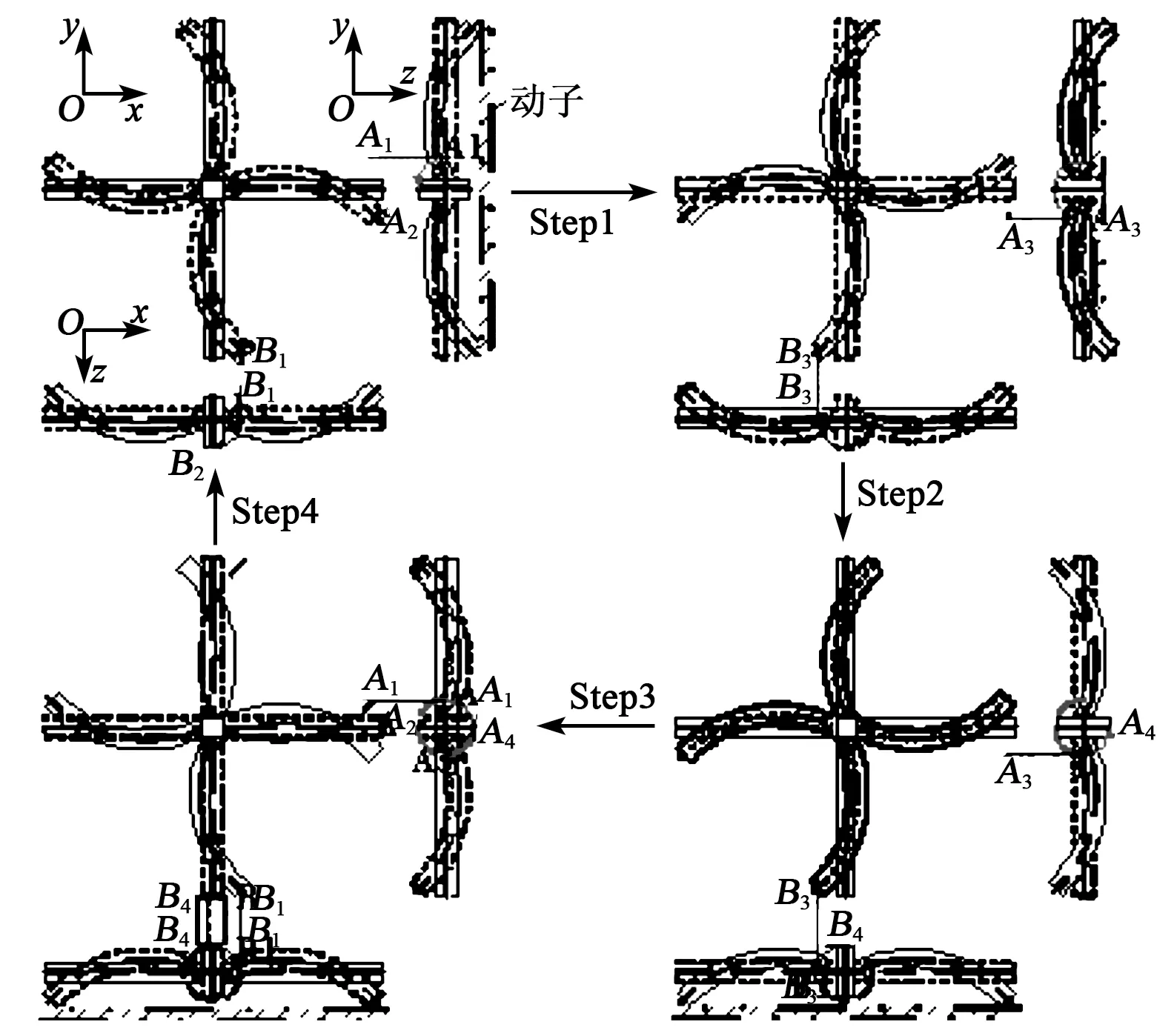
图5 1个周期(T)内定子驱动足运动轨迹

2 结构动力学优化

2.1 定子FEM建模

四音叉式定子结构复杂，故用ANSYS建立其有限元(FEM)机电分析模型。采用Solid185对定子基体网格化，采用Solid5对PZT网格化。定子材料采用磷青铜，材料参数为：密度8 270 kg/m3，弹性模量92.0 GPa，泊松比0.33。压电陶瓷材料选PZT8，由于定子基体既有阶梯结构又有空心圆柱结构，故采用自由网格划分。为了提高计算精度，压电陶瓷采用映射网格划分。图6为定子FEM动力学模型。

图6 定子FEM模型

2.2 频率一致性分析及定子尺寸设计

只有两相工作模态接近且不存在干扰模态，电机才能得到椭圆运动轨迹。通过分析图1所示定子各个尺寸对两相工作模态的影响，再借助灵敏度公式得到各尺寸对模态振型的灵敏度；然后，根据频率一致性的要求确定定子尺寸。定子的结构尺寸灵敏度为每单位尺寸变化引起定子工作模态的变化率，有

(4)

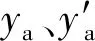
图7为各尺寸对工作模态的影响，取Δx=0.001 m，得到各尺寸灵敏度如图8所示。由图8可见，尺寸L1、L3、R2对频率的一致性影响较小，L2对面内弯振影响较大，R1则刚好相反，L4、H1、K1对频率一致性影响较大。通过上述频率灵敏度，以工作模态一致性为目标，得到定子优化尺寸如表1所示。优化后，定子的面外、面内工作模态分别为26 957 Hz和27 393 Hz(见图1(c)、(d))，频差为436 Hz，不超过工作模态的1.59%，频率一致性良好。定子两相模态振型纯正，有利于振子振动响应控制。

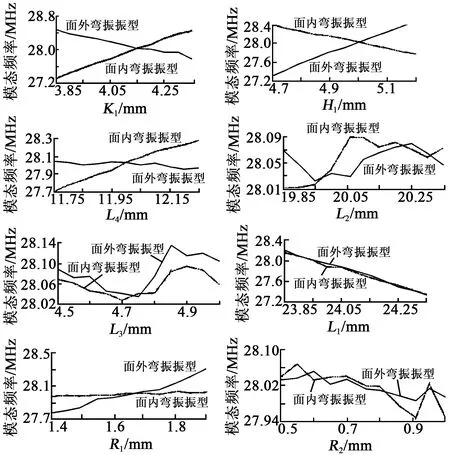
图7 各尺寸对模态的影响

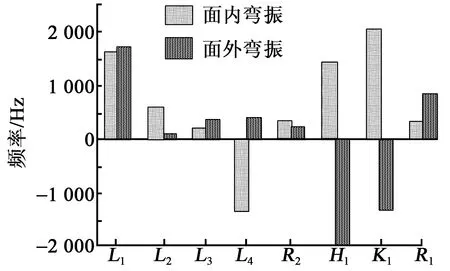
图8 各尺寸对模态的灵敏度

表1 四音叉式定子的优化尺寸

3 定子振动特性分析

3.1 谐响应分析

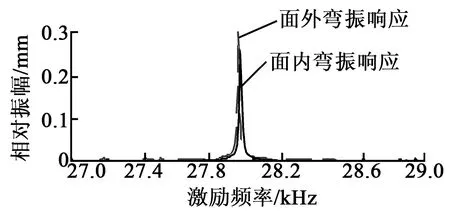
图9 定子驱动足的振动位移频响特性曲线

谐响应分析的目的在于计算出结构在不同激励频率下定子的位移响应，从而分析验证结构工作模态能否被激励，并为排除干扰模态提供依据。对优化后的定子FEM模型施加250 V的简谐电压，设置激励频率为26 900～29 300 Hz，加载子步数为100。仿真得到定子驱动足幅频特性曲线如图9所示。由图可见，在频率为27 950 Hz时，面内、面外弯振的幅值最大，工作模态频率一致性良好；在激励频率范围内，面内、面外弯振均只出现一个峰值，无干扰模态，故定子的振动调节特性良好。

3.2 定子瞬态分析

为了得到定子驱动足振幅，对定子进行瞬态分析。对定子FEM模型施加250 V、28 000 Hz，且相位差为π/2的简谐电压，求解得到驱动足位移响应如图10所示。由图可见，定子面内、面外工作模态均被有效激励，且x、y、z向振幅分别达到1.4 μm、0.8 μm、1.2 μm。图11为驱动足在xOz面内和yOz面内合成的椭圆运动轨迹。由图11可见，驱动足沿椭圆轨迹运动且椭圆轨迹呈扁平状，驱动弧较大，故电机有望得到较好性能。

图10 驱动足瞬态振动位移响应

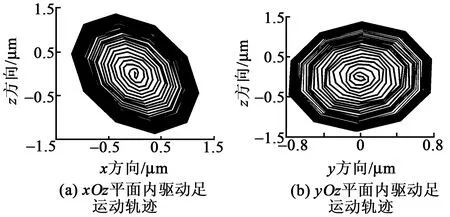
图11 定子驱动足椭圆轨迹

4 电机运动调节特性

因为电机采用交流信号驱动，故分别分析驱动电压、频率、相位差对驱动足运动特性的影响。首先在振子模型上施加不同幅值的驱动电压，得到驱动足调压特性如图12(a)所示。由图可见，驱动电压与驱动足振幅成近似的正比关系。当增大电压时，驱动足切向、法向振幅均增大。

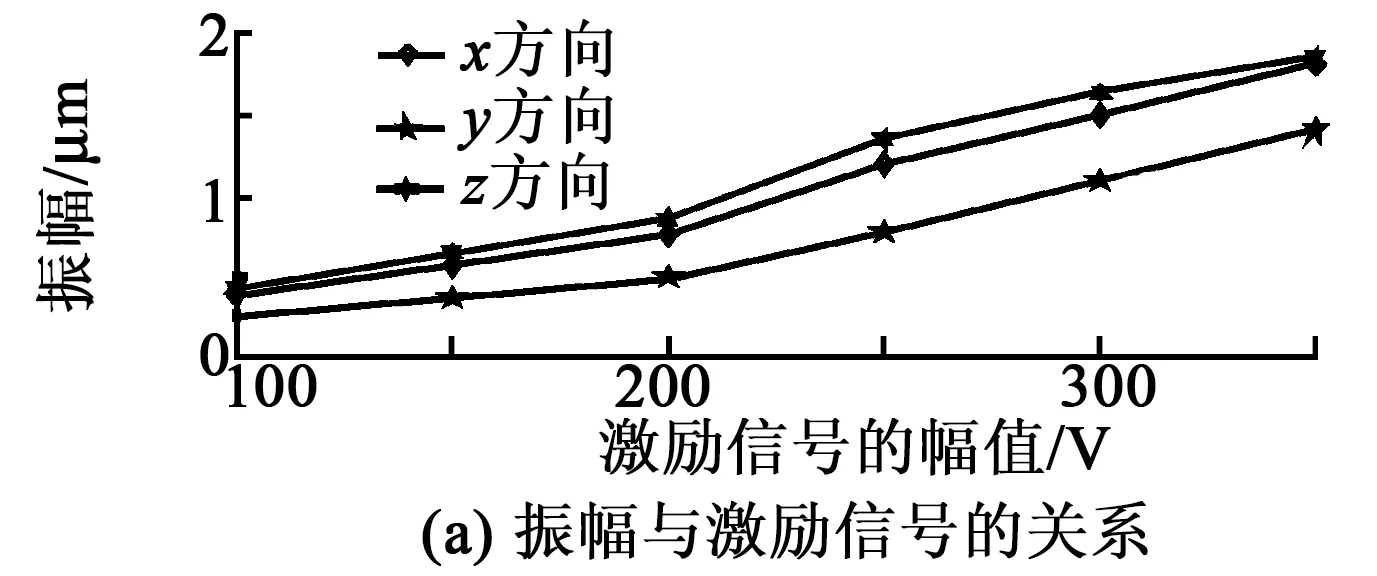
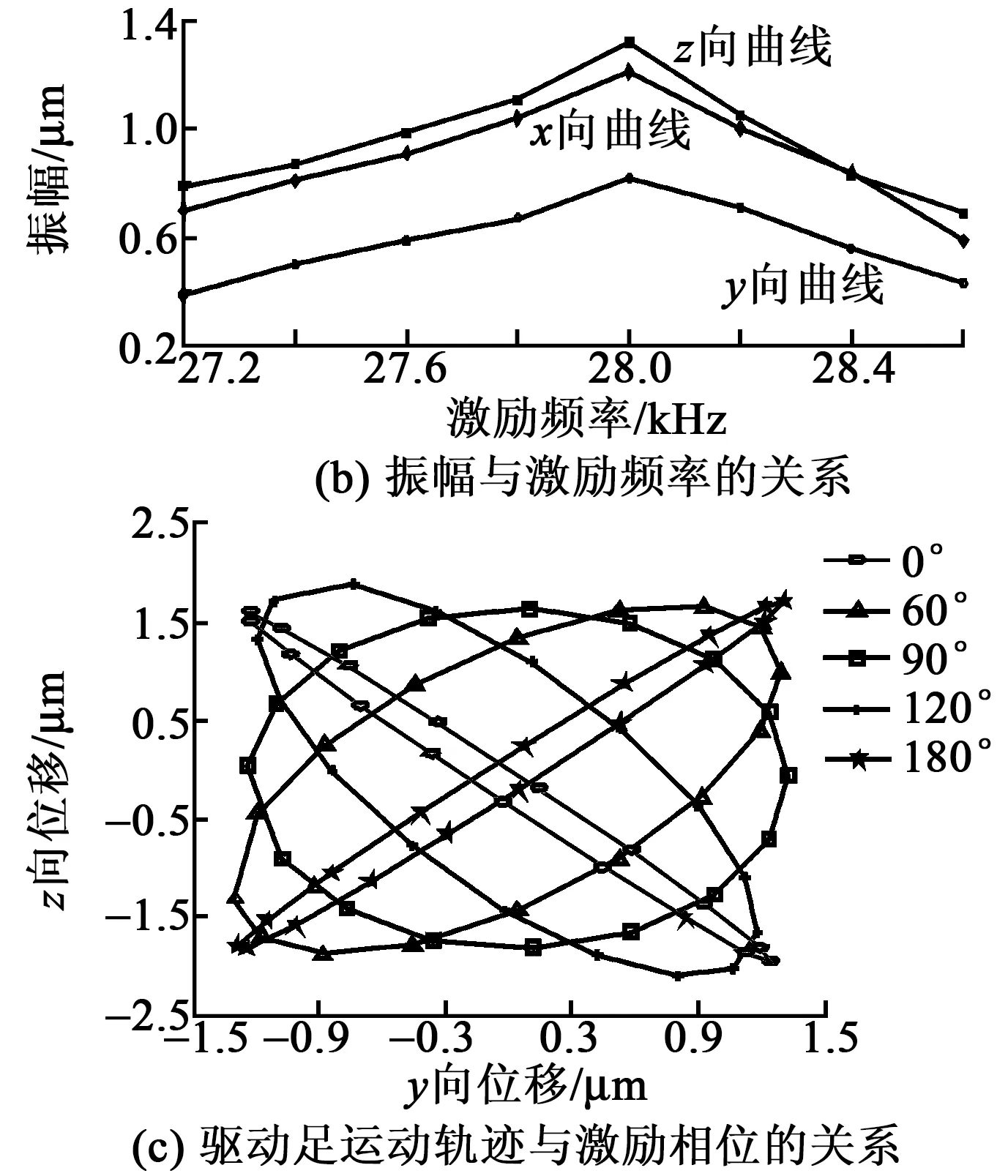
图12 电机运动调节特性

以频率不同的驱动信号激励振子，得到驱动足调频振动特性如图12(b)所示。由图可见，随着激励电源频率的增加，驱动足的幅值出现先增后减的现象，峰值出现在激励频率为28 000 Hz处。三相幅值的大小排列近似不随激励电源频率的改变而改变。

改变激励信号的相位差，得到相位差调节特性曲线如图12(c)所示。由图可见，当两相激励电信号的相位差为90°时，驱动足的输出呈正椭圆的运动轨迹，与式(3)完全符合。当激励信号相位差为0°、180°时，驱动足的输出近似为一条直线，电机不能运动。相位差为60°、120°时，电机输出形状近乎相同、朝向不同的椭圆运动轨迹。因此，相位差只有控制在90°附近区域内，电机才能正常工作。

5 电机装配结构设计

超声电机装配体除满足固定定子的效果外，应满足具有调节预紧力的作用及工作时运动方向不受干扰的特性。本文设计的装配包括定子、转子、防尘盖板、预紧盖板、预紧压环、转轴、轴承等零件，如图13所示。

图13 电机整体装配图

采用防尘盖板是为了减少外界灰尘、水等杂物对电机的运动产生干扰，延长电机的工作寿命。对定子施加的预紧力通过预紧盖板和预紧压环传递给定子驱动足。使用预紧压环施加预紧力是为了减少摩擦力，同时避免预紧盖板与转子运动产生干涉。四音叉定子通过中间部分的螺纹孔固定在底座上，定子中间安装转子轴承，用以固定驱动轴，提高旋转效率。

6 结论

1)提出四音叉式定子驱动的旋转超声电机，选定定子的面外、面内弯振作为工作模态。

2)确定振子压电极化供电配置模式，建立了定子参数化FEM模型及频率一致性优化动力学模型，得到定子音叉杆尺寸为24 mm×4.2 mm×5 mm，公共部分尺寸为12 mm×12 mm×3 mm。设计出电机结构。

3)模拟驱动足的椭圆轨迹，验证了电机原理。当驱动电压为250 V时，驱动足沿x、y、z向的振幅分别达1.4 μm、0.8 μm和1.2 μm。仿真得到电机调压、调频、调相位差驱动足幅值特性。