基于能陷理论的石英力敏谐振器集群的设计

陈福彬，田文杰，高锦春

(1.北京信息科技大学 传感器重点实验室，北京 100101；2.北京邮电大学 电子工程学院，北京 100876)

0 引言

石英晶体谐振器已广泛应用于晶体滤波器、振荡器等系统稳频控制器件中[1-3]。在发现石英谐振器的力敏效应后，利用石英晶体谐振器作敏感组件而构成的传感器应用在运动载体姿态、力(压力)、质量检测等领域[4-5]。本文打破传统石英晶片上单个电极构成谐振器的设计方法，在同一圆形晶片上设计多对电极构成力敏谐振器集群。同一石英基片上集成多个谐振器，谐振器之间存在耦合效应，依据能陷理论及其厚度剪切石英晶体谐振能量分布曲线，确定石英晶片的外形尺寸以及谐振器电极间距，保证各个谐振器能同时独立工作。利用共模抑制原理将谐振器集群输出频率信号作差频处理，温度等因素引起相同的频率漂移，但不产生差频输出，达到了抑制温度等因素干扰的目的。该石英谐振器集群可作为敏感元件应用于高精度的数字式惯性传感器以及相关检测系统。

1 石英力敏谐振器

石英晶体受外界机械压力作用产生压电效应。对石英晶体沿适当的角度切割成薄片，并在两面镀上电极，利用正-逆压电效应，电激励信号通过电极加到石英晶片上使其产生振动。当激励信号的频率与石英晶体的固有频率一致时，可形成谐振，该晶片即为谐振器。当谐振器的谐振特性受到外力的影响，利用这一特性可以制成石英谐振力传感器，如图1所示。

图1 径向受力的厚度剪切石英谐振器

2 能陷理论

能陷理论[4]是弹性波在晶片上传播时，当其频率大于电极区截止频率而小于非电极区的截止频率时，波可以在电极区自由传播，形成驻波，但在非电极区呈指数衰减，其振动能量集中在电极中心区，离开中心区时，振动能量则迅速减小。图2为圆形AT-切石英谐振器结构及电极区(中心区域)、非电极区弹性波传播示意图。

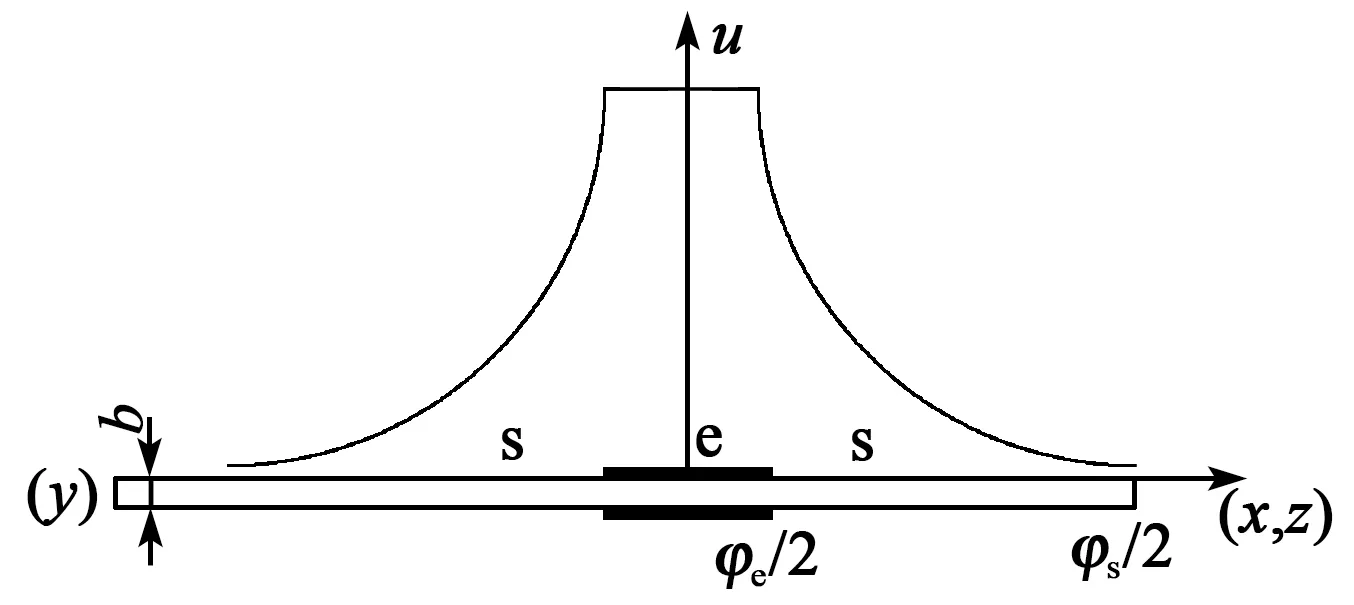
图2 圆形石英谐振器结构及弹性波传播示意图

弹性波在介质中传播的波动方程为

(1)

对于石英晶片，弹性剪切波的波动方程解为

u=Asinyej(β r-ωt)

(2)

式中A为剪切波幅度。

为了便于分析，假定波的能量沿各个方向传播是均匀的，r代表z或x方向的距离，y代表厚度方向的距离。弹性波在电极区(“e”区)可以自由传播，函数式为

(3)

式中βe为电极“e”区的传播系数。弹性波在非电极区(“s”区)内随着r的增大而按指数衰减，有

(4)

式中ηs为“s”区的衰减系数。

(5)

(6)

式中：p为泛音次数；b为石英晶片厚度；fe为电极区(“e”区)的截止频率；fs为非电极区(“s”区)的截止频率。

为了抑制能陷寄生，Shockley等建立了设计单电极石英振子的重要依据，即能陷判别不等式：

(7)

式(7)为多电极谐振器的设计提供了依据。

3 谐振能量的分布

3.1 非电极区能量的分布方程

根据能陷理论，弹性波随着离开“e”区距离r的增加而呈指数衰减，“e”区的谐振能量只有很少的部分进入“s”区，而能量与波的振幅是平方关系，因此，能量的衰减系数为2ηs。

(8)

“s”区的总能量取r→时，对式(8)求积分可得

(9)

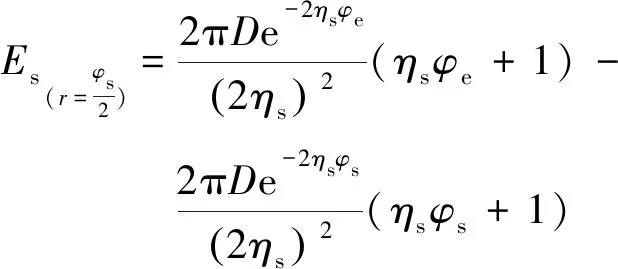
(10)

将式(10)与式(9)相除，可得环内能量与“s”区总能量的比值σ为

(11)

经变换得到“s”区能量分布的近似方程为

(12)

式(11)表示了σ、φe、φs和Ω0的关系，由此可以得到能量的分布曲线。

3.2 能量分布方程的求解

令

ηsφs+1=x

(13)

(14)

将式(5)、(7)取等号相乘，得到

(15)

再将式(15)代入式(14)，可得

(16)

最后将式(13)、(14)代入式(12)，得到一个超越方程，即简化的能量分布方程:

ex=k·x

(17)

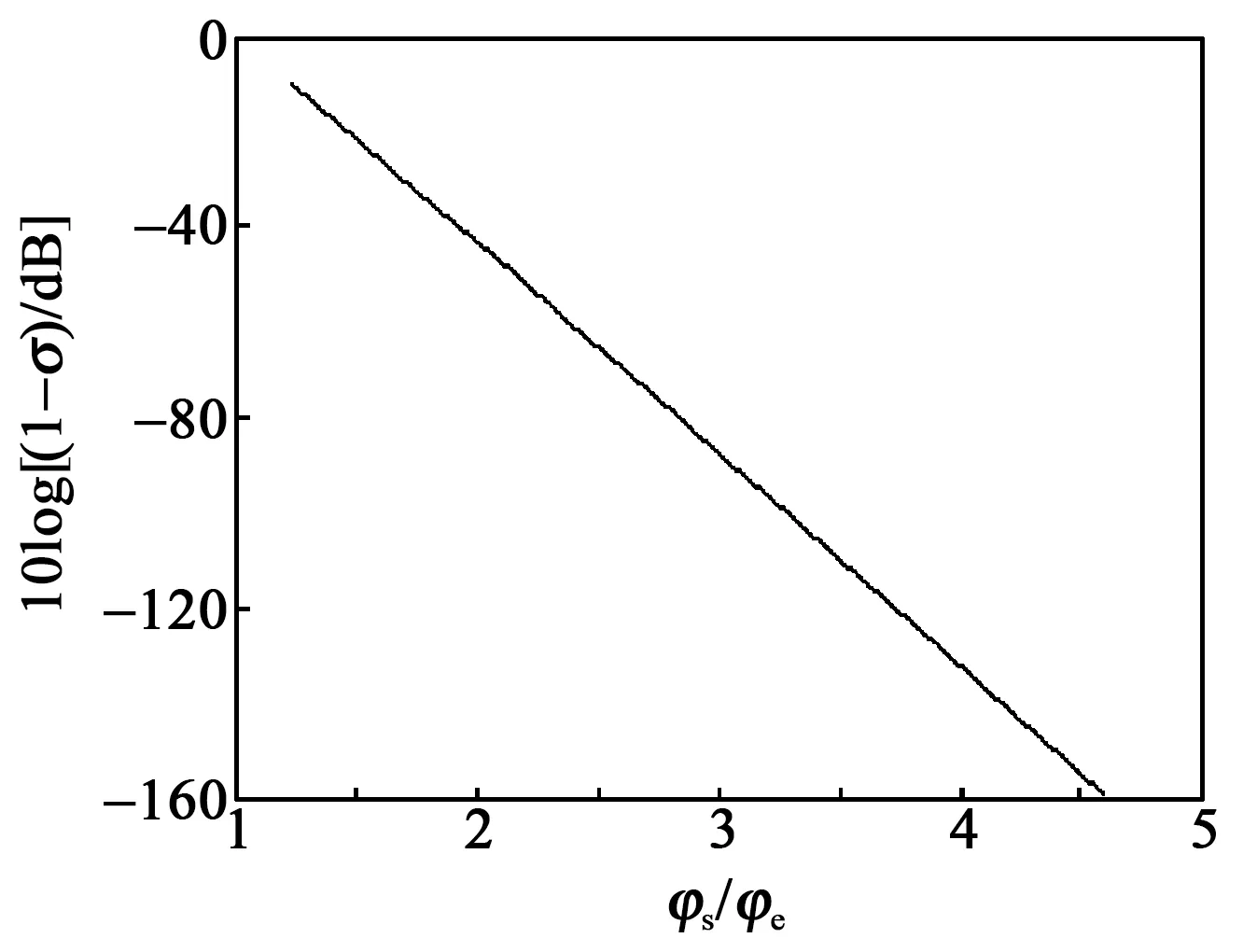
图3 能量分布曲线

由图3可知，进入“s”区的能量大部分集中在电极区的周围，当φs/φe=2 时，φs边缘上的能量仅约为“s”区总能量的-40 dB；而当φs/φe=3时，φs边缘上的能量很快下降到-80 dB，这时传到外边缘的能量已经很少。通过对能量分布曲线的分析可以得到晶片与电极尺寸以及多对电极间距的设计准则：

1)对于由电极电场激励的晶体谐振器，由图3可见，φs/φe取大或φe取小为宜。φe减小，可以减小谐振器的静态电容，也可以改善振荡器的稳定性。同时，φe减小，电极面积就减小，可以减小电极面积下晶片厚度不均匀所产生的杂散寄生。因此，在确保激励和高品质因数(Q)值的情况下，应尽量选取大的φs/φe值。

2)同一石英基片上集成多个谐振器，应避免谐振器之间的耦合。由图3可见，φs/φe=3时，φs边缘上的能量已下降到“s”区总能量的-80 dB，晶片直径取电极直径的3倍。实验证明，这样的取值合适。

利用该结论可以在同一圆形晶片上设计多对电极，形成谐振器集群。通过电极的合理设计，保证各个谐振器能同时独立工作，减小谐振器之间的相互干扰和噪声影响，以及改善频率的稳定性。

4 谐振器集群实验及分析

实验系统包括石英谐振器集群、6个独立振荡电路、恒温箱、频率计、频稳测试仪和数据处理，如图4所示。

图4 谐振器集群实验系统原理

4.1 温频特性

将谐振基频为20 MHz的6对电极谐振器集群置于温度试验箱内，在大气环境条件下测试-50～70 ℃对应的谐振器的谐振频率,得到的温度频率特性如图5所示。将谐振器对应的两个谐振频率作差频处理，得到的差频输出温度频率特性如图6所示。

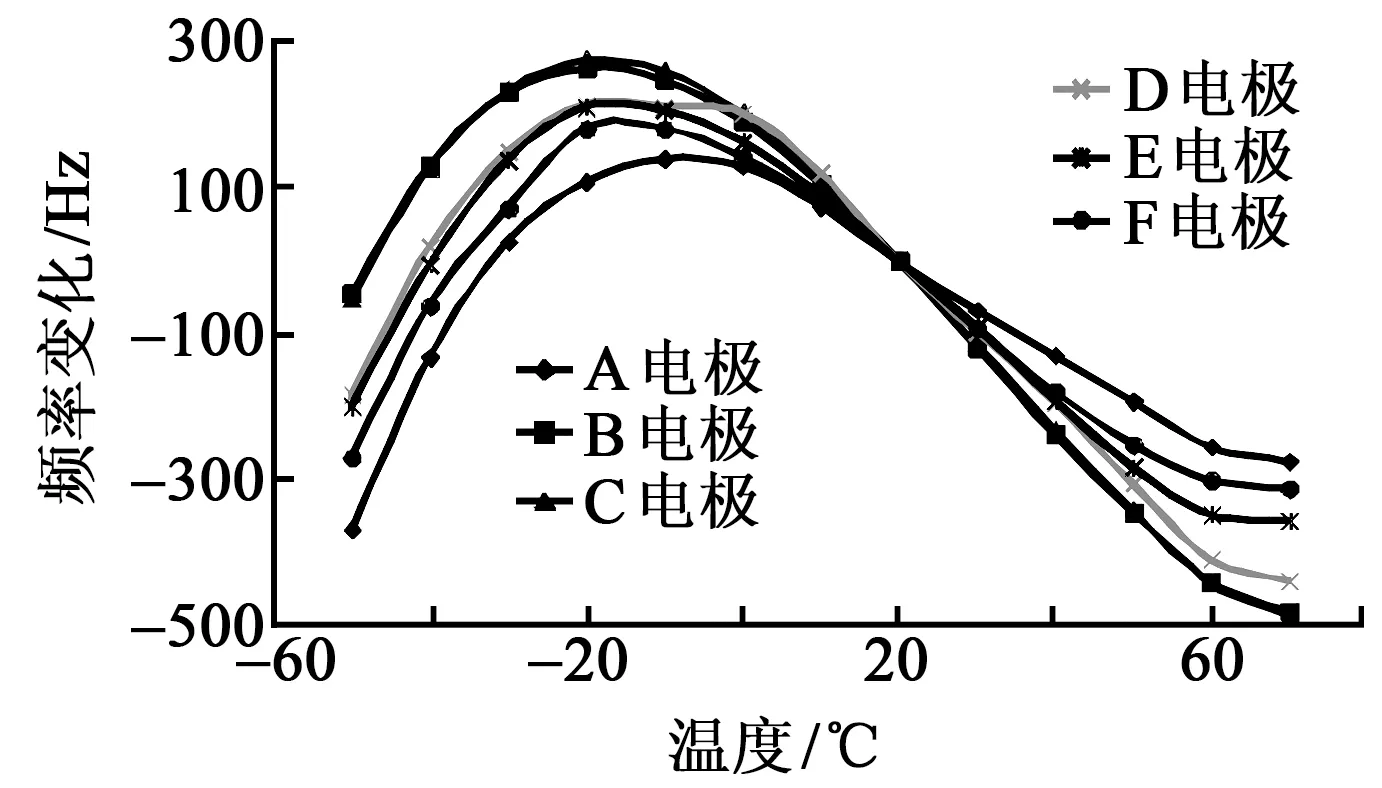
图5 谐振器集群的6个谐振器温度-频率特性

图6 谐振器集群差频输出的温度-频率特性

由图5、6可知，在温度为-50～70 ℃时，同一晶片上的6个谐振器谐振频率变化为-500～300 Hz，相对频率变化约为(-25～15)×10-6。其温度-频率特性与单电极谐振器的温度-频率特性相似，经过差频处理后，输出的频率变化为-300～200 Hz，相对频率变化约为(-15～10)×10-6。差频输出的温度-频率特性明显优于单个谐振器的温度-频率特性，谐振器集群具有较小的温度-频率变化率。

4.2 力-频特性

通过静力实验装置对石英晶体谐振器集群的力-频特性进行测试。基频为20 MHz，电极在石英晶片中心位置的传统单个石英晶体谐振器力-频特性的理论值为f=714.28F(Hz/N)，实验得到的力灵敏度略小于理论计算值。现在广泛采用的差动型双谐振器传感器系统力-频特性约为单谐振器的2倍，力灵敏度较低[5-7]。

石英晶体谐振器集群在径向力作用下，加力方位角为0°时，谐振器输出频率变化量为fA、fB、fC、fD、fE、fF。实验测试结果如表1所示。

表1 六电极石英谐振器的力-频特性

利用共模抑制原理将谐振器集群力-频特性差异较大的谐振器输出频率信号作差频处理，得到8组谐振器差频输出,并作最小二乘法线性拟合，得到力-频特性结果如图7所示。由图可见，差频输出力灵敏度系数最大为1 489.1 Hz/N，最小为9 66.56 Hz/N。将8组差频输出信号进行叠加求和，得到力灵敏度系数为9 992 Hz/N，提高了谐振器集群整体的力灵敏度系数。

图7 石英谐振器集群差频输出的力-频特性

5 结束语

本文利用能陷理论的结论，推导了石英晶体厚度剪切振动能量的近似分布方程，得到了能量分布曲线，提出了在同一圆形晶片上设计多对电极构成石英谐振器集群的设计依据，设计的石英谐振器集群满足抑制相互干扰的要求。利用共模抑制原理将谐振器集群输出频率信号作差频处理，抑制了温度等因素的干扰。将差频输出信号进行叠加求和，能提高石英晶体谐振器集群整体的力敏特性，力灵敏度系数可达9 992 Hz/N。利用这种具有显著力敏特性的石英谐振器集群作敏感元件构成的数字式惯性传感器系统(如加速度传感器、角速度传感器、水平姿态传感器等)具有广泛的应用前景。