退化数据驱动的气缸剩余寿命在线预测*

李 锋， 苑志凯， 何祯鑫， 王兆强

(1.火箭军工程大学二系 西安，710025) (2. 火箭军工程大学三系 西安，710025)

引 言

气缸是一种重要的机械元件，具有污染小、维护成本低等优点，被广泛应用于汽车生产线、半导体检查装置等工业设备。在气缸寿命预测方面，目前主要方法是通过加速寿命试验预测其完整使用寿命[1-3]，缺乏了对其使用过程中剩余使用寿命预测的研究。目前剩余寿命预测方法有很多，其中基于Wiener过程的剩余寿命预测模型因具有较为清晰的物理意义和良好的计算分析性质，应用最为广泛[4]。彭宝华等[5]将该模型与Bayes估计方法相结合，对金属化膜脉冲电容器的剩余寿命进行了预测。Wang等[6]将Wiener过程的退化建模应用于发光二极管的剩余寿命预测。李瑞等[7]用Wiener过程建立退化模型对自动加热电缆剩余寿命进行了预测。国内目前在机械元件剩余寿命预测方面对该方法应用较少，主要应用集中在对航空发动机的剩余寿命预测[8-9]。

笔者对传统的基于Wiener过程的剩余寿命预测模型进行改进，提出了一种基于退化路径的Wiener过程剩余寿命在线预测方法。选取CA2系列标准气缸为对象，进行了磨损退化实验，并将改进后的剩余寿命在线预测方法应用于该气缸，通过理论预测与实验结果的对比验证方法的有效性。

1 气缸剩余寿命预测模型构建

1.1 退化模型构建

气缸的故障原因有很多，主要的故障模式有密封圈磨损造成的过度泄漏和启动摩擦过大两种，这两种故障模式都是摩损累积退化失效过程。令X(t)表示气缸在t时刻的性能退化量，以一元Wiener过程可将退化过程{X(t),t≥0}描述如下

X(t)=X(0)+λt+σB(t)

(1)

其中：X(0)为气缸的初始退化(不失一般性，可令X(0)=0；实际中若X(0)≠0，可以对数据进行平移变换将其化为0[4,10])；λ为随机参数，用来刻画同类设备不同个体之间的差异；σ为共性参数，用来刻画同类设备之间的共性；B(t)表示标准布朗运动，用来刻画退化过程中的随机动态特性。

以上假设和规定是一元Wiener过程退化建模中的常用规定[5,8,9,11-12]。

在基于退化数据的可靠性建模中，通常将性能退化量超过某一预设的失效阈值作为产品出现故障的判定，这一阈值通常由实验、工程经验或工业标准等确定[6]。在这一故障定义下，产品的寿命和剩余寿命均用其性能退化量首次超过预设失效阈值的时间来表示，称之为首达时间。在首达时间的意义下，气缸的寿命T可表示为

T=inf{t:X(t)≥ω,t≥0}

(2)

其中：ω为失效阈值。

根据文献[13]可知，寿命T的分布为逆高斯分布，进一步推导可以得到，寿命T的概率密度函数(probability density function，简称PDF)为

(3)

1.2 剩余寿命预测模型构建

在1.1节已经建立了基于Wiener过程的气缸性能退化模型，并且得到了该模型下气缸寿命的概率密度函数。这一部分任务是依据观测到的历史退化数据，求解气缸剩余寿命的概率密度函数，从而实现对气缸剩余寿命的预测。目前大多数模型都是建立在剩余寿命的概率密度函数仅决定于当前时刻的性能退化量，笔者对传统的模型进行改进，建立一个依据退化路径对剩余寿命进行预测的模型。

定义气缸在t1,t2,…,tk时刻的退化数据为X1:k={x1,x2,…,xk}，表示气缸在tk时刻前的退化路径。在首达时间的意义下，气缸的剩余寿命Lk是指从当前时刻开始到性能退化量X(t)首次超过失效阈值的时间。因此，气缸的剩余寿命可表示为

Lk=inf{lk:X(lk+tk)≥ω|X1:k}

(4)

其中：lk表示剩余寿命Lk的实现。

由一元维纳过程的齐次马尔科夫性和独立增量性质，可得到剩余寿命Lk在给定随机参数λ和退化数据X1:k时的概率密度函数，表达式为

(5)

要实现气缸剩余寿命的预测，需要消除式(5)中的未知参数，求出气缸在退化路径X1:k下剩余寿命的概率密度函数fLk|X1:k(lk|X1:k)。下面思考如何根据已知的退化路径X1:k对未知参数进行估计，求出fLk|X1:k(lk|X1:k)。

考虑到退化模型中参数λ的随机性，可以通过全概率公式来求解fLk|X1:k(lk|X1:k)

(6)

2 剩余寿命预测模型求解

前面已经给出了气缸在退化路径下剩余寿命概率密度函数求解的全概率公式，要实现剩余寿命的预测还需求解随机参数λ的后验分布，并对未知参数进行估计。

2.1 参数λ后验分布的Bayes估计

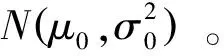
(7)

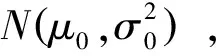
(8)

由于λ|X1:k服从正态分布，可以得到

(9)

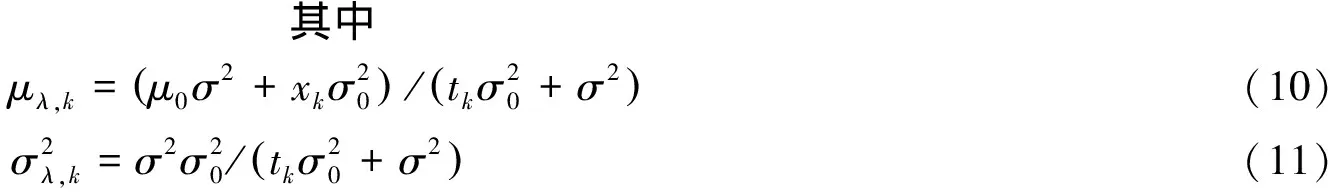
2.2 基于EM算法的未知参数估计

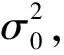
为实现对Θ的估计，需求解似然函数

lk(Θ)=lnp(X1:k|Θ)

(12)

其中：p(X1:k|Θ)为退化路径X1:k的联合分布密度函数。

在退化数据X1:k下的最大似然估计量为

(13)

由于参数λ的随机性和不可观测性，式(13)将很难直接求解，这里引入期望最大化算法(expectationmaximizationalgorithm，简称EM算法)对其求解。EM算法的核心思想是通过添加数据包括“缺损数据”、未知参数等，利用简单的迭代运算，求解复杂分布的极大似然估计。算法分两步：a.求期望，称为E步；b.求极大值，称为M步。笔者通过添加未知参数λ，利用EM算法求解似然函数lnp(X1:k,λ|Θk) 实现对p(X1:k|Θ)的极大似然估计，方法如下。

E步

(14)

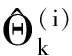
M步

(15)

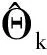
首先求解添加未知参数λ后的似然函数

lnp(X1:k,λ|Θk)=lnp(X1:k|λ,Θk)+lnp(λ|Θk)

(16)

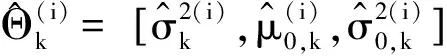
(17)

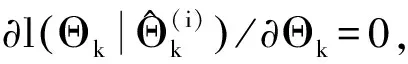
3 气缸剩余寿命预测在线更新算法

前面求解了p(λ|X1:k)并对未知参数Θ进行了估计，完成了剩余寿命的PDF随退化路径X1:k的在线更新的准备工作。实现剩余寿命的PDF随退化路径X1:k的在线更新方法如下。

首先，由全概率公式可得

(21)

进一步推导可得到剩余寿命PDF的在线更新解析式为

(22)

到此已经完成了气缸退化模型的建立、剩余寿命概率密度函数的求解以及未知参数的估计和在线更新。基于以上工作，可总结得到气缸剩余寿命实时预测的算法如下：

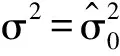
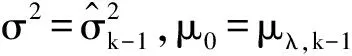
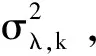
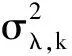
5) 当观测得到tk+1(k≥1)时刻的新的退化数据xk+1后，重复步骤 2，3，4实现剩余寿命的更新。

4 实 验

4.1 问题描述

气缸的故障原因有很多，主要的故障模式有密封圈磨损造成的过度泄漏和启动摩擦过大。因气缸过度泄漏故障通常发生在启动摩擦过大之后[2]，笔者针对启动摩擦过大造成气缸失效的退化过程进行研究。气缸的最小启动压(minimumoperatepressure，简称MOP)可以用来表征启动摩擦力的大小，且测量方便，因此选取该指标作为气缸的性能退化量。ISO1997 3-3[14]规定在正常使用状态下，MOP应小于120kPa，因此将气缸的失效阈值定为120kPa。气缸的寿命通常用作动次数(cycles)表示，活塞在缸筒两端往复一次记为一个作动次数。

笔者在正常工作状态(23℃)下对3个CA2系列标准气缸样本进行了磨损退化实验。实验中供气压力为0.70MPa，活塞杆速度为600mm/s，负载为3kg，频率为1Hz。实验气缸缸径为φ50mm，行程为250mm。经过近10个月18×106cycles的测试，每隔5×105cycles记录气缸MOP值，最终获取3组实验数据。只有第3组MOP退化实验数据最终超过了失效阈值，所以选取第3组实验数据(37个采样点)验证本研究剩余寿命预测方法的准确性。第3组MOP退化实验数据的退化路径如图1所示，最终在采样点15.5×106cycles时MOP超过失效阈值，将此时刻作为气缸的失效时刻。

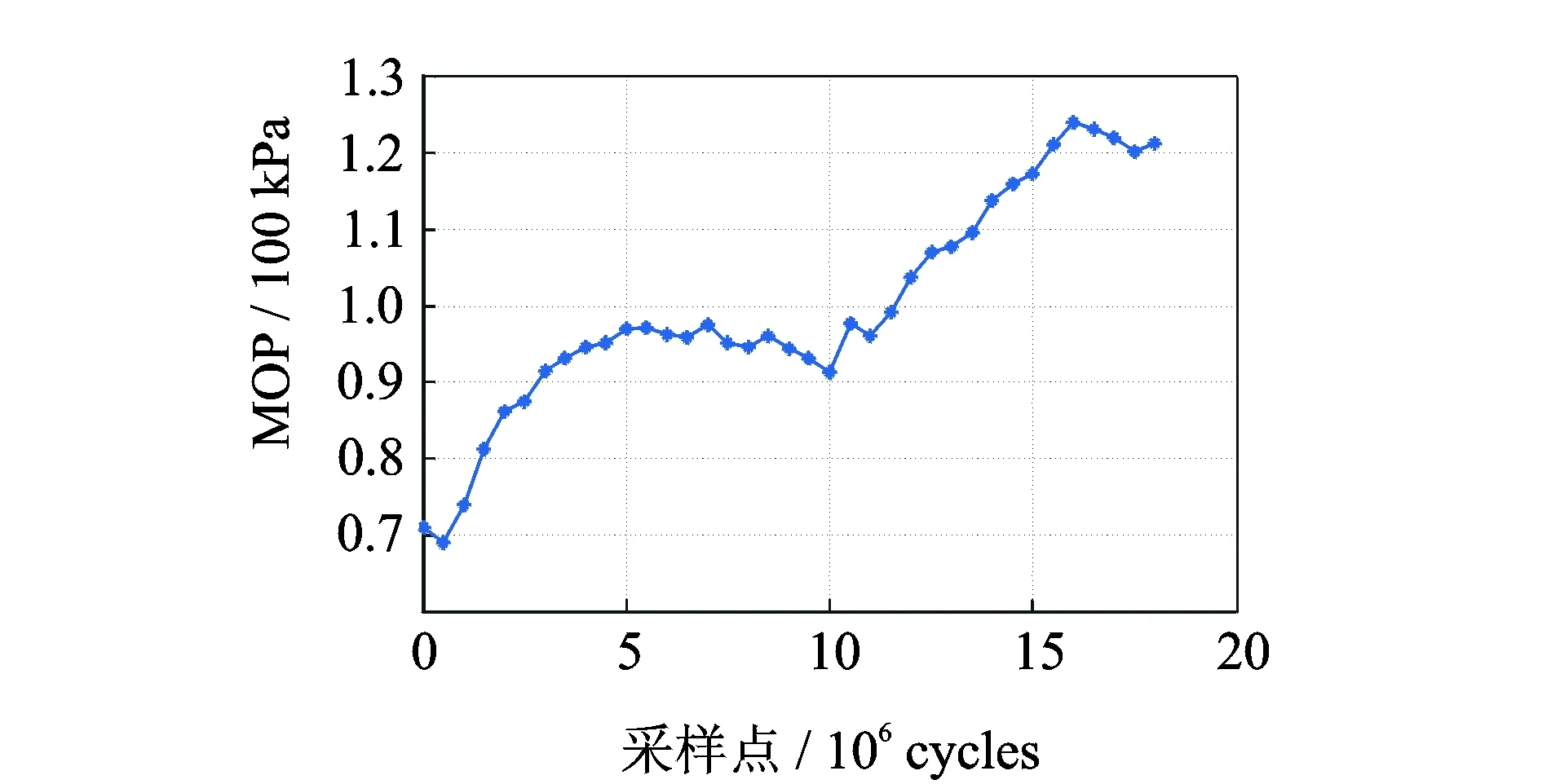
图1 气缸MOP退化路径Fig.1 MOP degradation path of the cylinder

4.2 实验结果及分析

把气缸MOP退化实验数据带入笔者提出的剩余寿命在线预测方法进行计算，并与文献[5]中的剩余寿命的预测方法进行对比，验证本方法的可行性和准确性。同时，由于所提算法需要给定初始参数，这一部分也将通过调整初始参数对本方法的参数初始值敏感性进行分析。为方便叙述，下面均将文献[5]中的剩余寿命的预测方法称为文献[5]方法。

4.2.1 选择合适参数时的预测结果

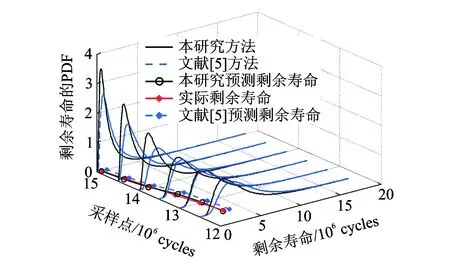
图2 最后6个采样点剩余寿命的PDFFig.2 The PDF of the residual life at the last six points

为进一步从数值角度比较本研究方法与文献[5]方法对气缸退化数据的在线预测能力，采用均方误差(meansquareerror，简称MSE)作为评价指标[15]。定义tk时刻的均方误差为

(23)

其中：k为第k个采样点；xk为第k个采样点实际退化数据；E(X(tk))为预测的第k个采样点退化数据X(tk)的期望。

经计算，在整个退化过程中，两种方法得到的MSE如图3所示。由图3中两条曲线的对比可以看出，在整个气缸退化过程中本研究方法的MSE几乎始终要小于文献[5]方法，说明本方法对气缸退化数据的预测要更准确。

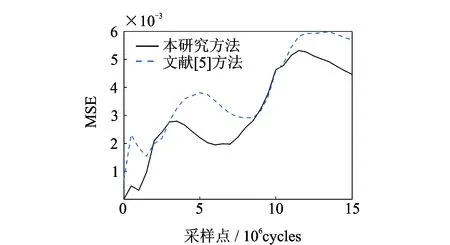
图3 两种方法的MSE对比Fig.3 Mean squared error of the two methods

4.2.2 参数初始值敏感性分析

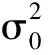
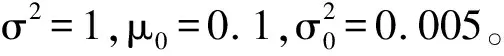
为比较参数初始值对气缸剩余寿命预测结果的影响，选取气缸MOP首次超过失效阈值前的6个采样点，在3种初始参数设置情形下分别计算它们的MSE，计算结果如表1所示。3种情形下的MSE都很小，可见本研究方法对初始参数给定不敏感。

表1 3种情形下最后6个采样点的MSE

Tab.1 The mean squared error of the three cases at the last six points

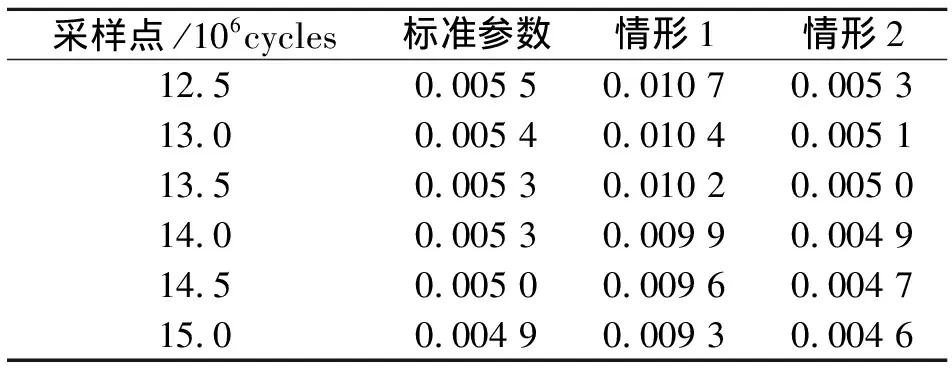
/106cycles1212.50.005 50.010 70.005 313.00.005 40.010 40.005 113.50.005 30.010 20.005 014.00.005 30.009 90.004 914.50.005 00.009 60.004 715.00.004 90.009 30.004 6

5 结 论

1) 在小样本情况下与文献中同类方法相比，本研究方法能更准确地预测气缸剩余寿命且预测的不确定性更低。

2) 该方法对初始参数精度要求不高，具有较强鲁棒性。

3) 下一步可以通过融合其他相关信息来提高本研究方法预测的准确性和可靠性，例如融合同种(类)产品的离线退化数据、寿命数据等。