水电机组振动信号的自适应VMD分析
张长伟,徐成劢,王卫玉,郑 阳,陈启卷
(1.国网浙江省电力有限公司紧水滩水力发电厂,浙江 丽水 320000;2. 武汉大学 水力机械过渡过程教育部重点实验室,武汉 430072)
在实际的水电机组运营生产中,机组的不稳定性随着运行条件的复杂化变得越来越强烈,不稳定性问题一般都是由水力因素、电气因素、机械因素引起,而故障与诱因之间并不是一一对应的关系,这也是水电机组故障诊断的难题[1-4]。
水电机组振动信号具有非线性非平稳性特点。常用的快速傅立叶变换FFT适用于分析更规则的线性信号[5];虽然小波变换[6]在分析非平稳信号方面具有一定的优势,但它没有适应性。同时,如果存在强噪声,小波变换会产生明显的信号混叠现象[7];经验模态分解(EMD)新型自适应信号时频处理方法,从不同层面对振动信号进行分解,获得一系列固有模态分量。然而,当故障发生时,振动信号的不稳定性、非线性增强,用经验模态分解会出现较强的端点效应和模态混叠问题[8],这也是经验模态分解方法的局限性。
集合经验模式分解(EEMD)方法是一种基于EMD开发的新型信号分析技术。它在研究信号的局部特征方面具有一定的优势。EEMD方法通过向原始信号添加足够的零均值白噪声集,以及通过EMD分解和IMF分量求和来抑制EMD分解的最终效果和模态混叠。但是,EEMD方法仅部分抑制了最终效果和模态混叠。仍存在 EMD分解中出现的一些问题,并产生了加入噪声残留和原信号噪声影响等一系列新的问题,影响EEMD方法在实际中的应用。
为解决EMD、EEMD等方法的局限性,一个新的信号处理方法----变分模态分解方法被提出,该方法有较为严格的数学理论基础支撑,计算速度快,但是不能够自主分解不同的振动信号,需要通过设定参数数值从而保证其优越的信号分解效果[9,10]。
为了能够准确分析水电机组运行状态,提升振动信号分解效果,获取较为明显的信号特征,本文提出一种适用于水电机组振动信号的自适应VMD分析方法,首先选择对信号分解效果影响较大的VMD预设参数,然后通过回溯搜索算法计算最佳参数数值,使得信号分解结果真实有效。对某水电机组振动信号分析处理的结果显示,本方法在处理水电机组振动信号上面具有较大优势,是一种行之有效的信号处理方法。
1 基本原理
1.1 变分模态分解
在变分模态分解中,固有模态分量(IMF)是一种调幅调频信号。第K个分量信号uk(t)如下所示:
uk(t)=AK(t) cos[ϑk(t)]
(1)
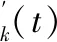
VMD对每一个分量用hilbert变换构造分析信号,得到单边频率谱,然后根据傅立叶变换的特殊性质,将分解所得IMF分量的频谱在基带中展现。最后利用Gauss解调法计算带宽。最终的目标是让得到最低的模态分量带宽之和,其计算公式被表示为:
(2)
(3)
式中:{ωk}为VMD分解所得结果;{ωk}为每个IMF分量的中心频率;K为分解所得的IMF个数;限制条件为分解后所得IMF分量可以重新组合成源信号。
将求解最优化问题更换为一个求解无约束的问题,为此我们加入一个惩罚项和拉格朗日乘数,公式如下所示:
(4)
式中:α为惩罚系数;λ为Lagrange乘子参数。
VMD使用交替乘法器方法(ADMM)对该方程进行求。获得K个IMF分量。VMD算法运算流程参考文献[8]。
1.2 全局敏感性参数分析----Sobol法
参数敏感性有两个目的:确定对信号分解结果造成影响较大的预设参数;去除对信号分解影响较小的参数,从而有效缩减优化过程的计算时间。Sobol方法是一种可以寻找对信号分解结果影响最大的单个或几个参数选择方法,不仅能够计算单一参数对分解结果的影响程度,还能够计算几个参数组合对信号分解的影响程度。具体计算方法参考文献[11]。
1.3 回溯搜索优化算法
回溯搜索算法(Backtracking search Algorithm, BSA)是一种全以局最小化计算器为基础的,以社区为优化目标的搜索算法。回溯搜索算法的计算过程运算步骤如下[12,13]:
(1)初始化种群P。
Pi,j~U(lowj,upj)
(5)
式中:i为从1到N的整数值;j为从1到D的整数值;N为种群规模大小;D为求解问题的数量;U()代表了均匀分布;Pi,j是遵循均匀分布分布原则的随机数。
(2)选择1。选择1是一个选择历史种群oldP的过程。
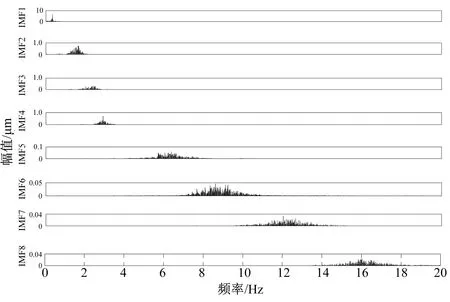
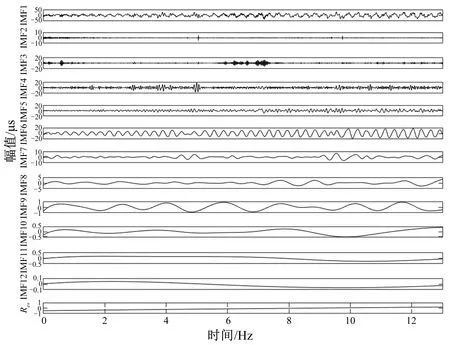
ifa (6) (3)突变。在确定了历史种群后,就对群体中的个体进行随机排序,并将排序后的结果重新赋予历史种群oldP。 Mut=P+F(oldP-P) (7) 式中:F为变异程度系数,F=3randn;rand为符合标准正态分布的随机值。 (4)交叉。回溯搜索算法的交叉过程是两种等概率交叉策略的组合: (8) 式中:dimrate为交叉概率;dim为问题维数。 两种方法的等概率随机方式组成了回溯搜索方法的交叉过程,最终产生了新的种群M。 (5)选择2。对比历史种群P和新生种群M的相同个体适应度,当新生种群M中的第Mi个体适应度小于Pi时,将Mi作为当代种群。 (9) 随后,开始又一轮计算,在本方法中,将信息熵作为适应度函数。 (6)判断。当运算结果满足算法终止条件时,输出当前最优解; 否则,重新返回选择1阶段进行计算。 信息熵是一种评价信息混乱程度特性的指标。固有模态分量由实测信号经自适应VMD分解所得,IMF分量中包含的有效机组特征的信息越多,噪声成分越少则该分量的熵值越小,说明该信号的规律性越强。根据信息熵值的这一特性,本文选择信息熵作为回溯算法的寻优适应度函数[14,15]。信息熵计算如下所示: (10) 预设参数数值的不同,分解所得的固有模态分量也有变化。需要预设的参数共有4个:模态数K、惩罚参数α、保真度τ、判别精度tol,针对不同的研究对象,我们所需要优化计算的预设参数也不相同。文献[15]通过粒子群算法对惩罚参数α、模态分解数K值进行优化,有效的从滚动轴承振动信号终获取所需特征。文献[16]通过确定模态数K,保真度τ的数值,有效分析水电机组上机架信号。每个参数对机组不同位置振动信号分解结果的影响大小程度有所不同。本文提出一种参数敏感性的分析方法----Sobol方差分解法,该方法可以选取对分解效果影响较大的参数,大大地降低了优化所需时间。 Sobol方差分解法是一种全局敏感性分析方法。相对于局部寻优法通过分析单个参数的改变,得到该参数对目标的影响,Sobol法可计算不同的参数组合对分解结果的影响程度,得到较为全面的结果,有效地避免了局部最优解的发生。 回溯搜索算法与枚举的搜索尝试过程具有相似性,是一种全新的全局寻优算法。相较于传统的遗传算法、蚁群算法,回溯算法可以在保持原有的寻优特点的基础上,大幅度缩短寻优时间。 Sobol法与回溯算法都是以适应度函数为目标进行搜寻优化。基于信息熵值对信息混乱程度评价的特点,选择信息熵作为适应度函数。既能够保证寻优过程有效性的,也能保证其寻优搜索方向的一致性。基于此,本文提出了一种自适应VMD方法(见图1),可以针对不同类型水电机组振动信号自动调整参数数值,实现分解效果最优化,方法步骤如下: 图1 自适应VMD分解算法 (1) 加载水电机组振动信号。 (2) 以信息熵作为评价指标,通过Sobol选择对该振动信号分解影响较大的预设参数(K、α、τ、tol)。 (3) 将被选择的预设参数作为回溯算法的寻优目标,为保证一致性,同样将信息熵作为适应度函数。 (4) 对加载的振动信号进行VMD分解。 为了验证提出方法的有效性,以某电厂开机升转速过程上导Y向水平振动信号为例进行说明。水电机组开机过程中的振动信号具有非平稳、非线性特点,能够在一定程度上表现机组运行状态。机组额定转速为200 r/min、额定出力为50 MW。图2为开机过渡过程的上导Y向水平振动信号波形。 图2 上导Y向水平振动波形图 从图2可以看出,上导Y向的振动信号中振动幅值随时间逐渐变大,但最终趋于稳定,主要是初始过程的小振幅、振幅随时间增加、达到稳定转速后保持稳定3个阶段。首先利用Sobol法选择对上导Y向振动信号分解效果影响较大的参数,计算结果如表1所示。 表1 参数影响程度 根据表1的结果,模态数K、惩罚因子α、保真度τ对于分解结果有较大影响。因此在第二步,选择这3个参数,用回溯算法对其数值优化计算,图3是对实测信号进行分解后所得的固有模态分量。图4是相对应的频谱图。回溯算法在寻优过程计算所得的最优参数K=8、α=2337、τ=0.1。 图3 Y向振动VMD分解结果 图4 IMF分量频谱图 VMD分解Y向振动信号所得结果及对应频谱如图3和图4所示。分析可得到结论:IMF分量可分为3个部分。IMF1为第一部分,与原始振动信号去噪后所得信号较为相似,能够粗略表达上导Y向振动在机组升转速过程中的大致变化规律。IMF2~IMF4为第二部分,可以看到每个分量中都存在一个纺锤形信号,并且随开机时间的变化,纺锤形信号的位置逐渐向后移动。虽然还存在一定的模态混叠现象,但仍然可以看到其规律性,可以表达该机组在开机升转速过程中的振动变化规律。其中IMF4的频率为3.3Hz,对应机组1倍频。第三部分则为IMF5~IMF8,可以明显看出为噪音干扰分量,频率较高而能量较低。 EEMD通过在信号中加入多次均值为零、方差相等的随机白噪声,能够保证对每个模态函数在时域上的连续性的同时减少了模态混叠现象。EEMD通过叠加白噪声使信号中的频率成分能在整个时域内获得合适的时间尺度,能够在一定程度上减少因各种频率成分导致的模态混叠,使得IMF分量失真较小,具有明确的物理意义。相对于基础的EMD方法,EEMD方法减少了模态混叠现象的同时也在一定程度上抑制了端点效应的发生。 为说明自适应VMD方法的高效性,与集合经验模态方法进行比较。EEMD分解波形及频谱如图5和图6所示。可以看出,波形图中低频率低能量的虚假分量较多,并且存在大量的模态混叠现象,分解所得IMF分量不能表示明确的物理含义,对机组状态评价的准确性造成影响。对比两种信号处理方法,VMD在处理非平稳性、非线性信号时,可以有效地避免模态混叠现象的产生,提取的IMF分量可以表征一定的物理意义,分辨率较高,具有较好的适用性与优越性。 图5 EEMD分解波形 图6 EEMD分解频谱图 (1)本文针对VMD不能够自主调整预设参数的缺陷,提出了一种基于参数敏感性分析与回溯算法的自适应VMD信号处理方法,该方法在保证较好分解效果的同时,有效减少了寻优时间。 (2)对上导Y向实测信号的分析结果表明,在振动信号分解方面,相较于集合经验模态分解方法,自适应VMD算法大幅度减少了模态混叠的出现,准确提取了信号特征,是一种具有较强适应性的信号处理方法。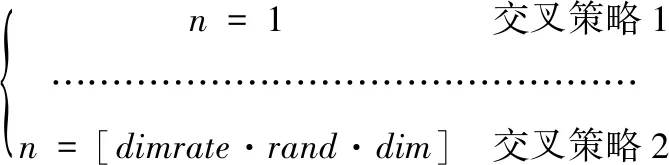
1.4 信息熵评价指标
2 基于全局寻优的VMD方法

3 实测信号分析
3.1 实测信号VMD效果分析
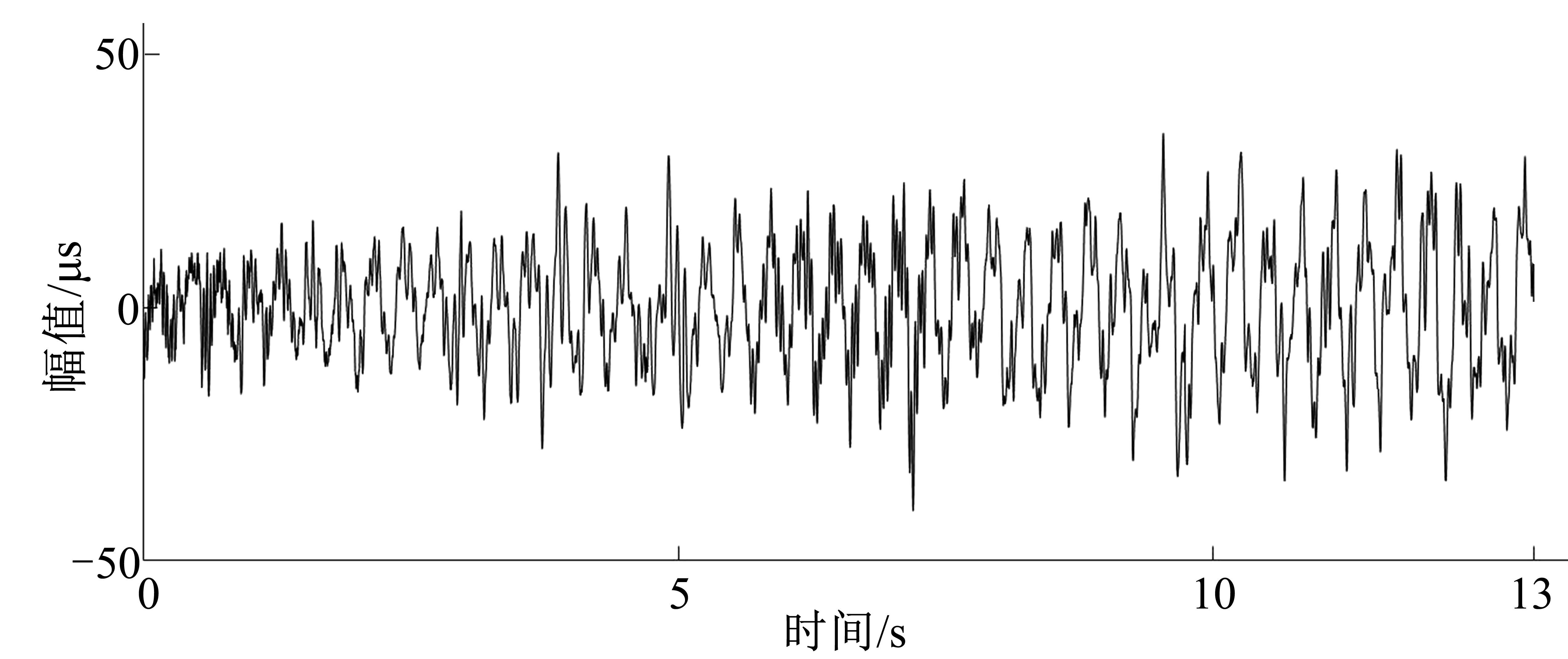

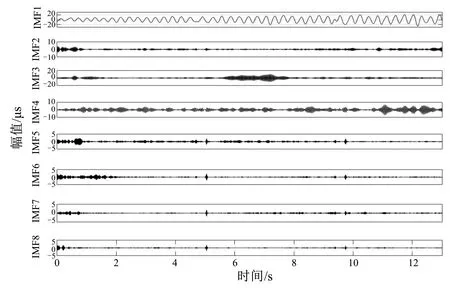
3.2 实测信号EEMD分解对比

4 结 语

