基于改进不变矩与概率神经网络的水电机组轴心轨迹特征提取研究

袁喜来，刘 东，胡 晓，刘 冬

(1. 湖北能源生产技术部，武汉 430072；2. 武汉大学动力与机械学院，武汉 430072)

水电机组的安全稳定运行对于提高电力系统稳定性具有重要意义，对水电机组进行状态监测和特征提取是一项十分必要的工作。目前在水电机组故障诊断中，常用的诊断方法是对机组振动波形信号进行频谱分析，而转子轴心轨迹作为机组实际运行的信息载体，其形状特征和进动方向对于判断机组运行状态非常重要[1]，因此当监测数据间存在较强的非线性关系、尤其是频谱信息缺乏有效性时，识别轴心轨迹对于水电机组的故障诊断具有十分重要的意义。

究其本质而言，轴心轨迹的识别可以看作是对二维图像的分类处理和模式识别问题。轴心轨迹的特征提取方法理论众多，比较有代表性的有特征矩理论、傅里叶描述子理论、高阶相关特征、链编码直方图与形状编号法等。孙国栋等[2]针对旋转机械轴心轨迹的识别准确率低、识别速度慢等问题，提出了基于高度函数的旋转机械轴心轨迹识别算法，并结合BP神经网络进行识别验证；张征凯等[3]通过联合轴心轨迹的分形特征和几何特征对旋转机械的转子运行状态进行了评定，获得了良好的区分度；付婧等[4]采用统计分析的方法定义了轴心轨迹的识别参数，并对机组不同负荷下的轴心轨迹进行了特征识别；Wang, CQ[5]等提出链编码与概率神经网络相结合的方法对液压发电机组轴心轨迹进行识别，表明了该方法的有效性。

HU不变矩[6]是由M-K HU在1962年提出的用于表征图像区域的几何特征的一组矩向量，被广泛应用于图像的特征提取与识别领域。祝晓燕等[7]利用转子轴心轨迹图像不变矩与支持向量机相结合的方法对转子故障进行诊断；李友平等[8]提出将灰色理论关联度与不变性矩相结合对水电机组轴心轨迹进行特征提取，并取得了较好的识别效果；刘其洪等[9]结合HU不变矩，提出一种基于LabVIEW的轴心轨迹故障自动识别的新方法，并对旋转机械转子不对中故障下的轴心轨迹进行了有效识别。本文提出了将改进HU不变矩与概率神经网络相结合的方法用于水电机组的故障诊断，通过改进HU不变矩算法对经小波降噪后的水电机组典型的轴心轨迹进行特征提取，构建轴心轨迹的矩特征向量，并利用概率神经网络训练时间短、分类准确的优点对提取的轴心轨迹特征向量进行识别分类，从而达到对机组不同运行状态进行判别的目的。

1 不变特征矩原理

1.1 矩及其不变性

对于定义在o-xy平面的二维图像f(x,y)∈L(R2)，其在R2平面上的p+q阶原点矩为：

(1)

f(x,y)表示图像在二维平面上的质量密度，离散状态下图像的p+q阶原点矩为：

(2)

此时的p+q阶矩依赖于图像在坐标系中的位置，不满足平移不变性，经变换后得到满足平移不变性的p+q阶中心矩：

(3)

为进一步满足伸缩不变性，将μpq进行正规化处理，得：

(4)

对ηpq进行进一步处理得到满足平移、伸缩和旋转不变性的7个完备的2阶和3阶特征矩φ1～φ7：

1.2 离散状态下的改进不变矩

在水电机组实际信号采集中，所得机组信号为离散信号，而7个特征矩在离散状态下并不具有伸缩不变性[10]。本文采用改进不变矩算法[11]，在原有7个特征矩的基础上构建新的不变矩，使其满足在离散状态下的平移、伸缩和旋转不变性。新的不变矩特征向量为：

(6)

本文将φ1～φ6作为新的矩特征向量用于水电机组轴心轨迹的特征提取。

2 概率神经网络算法

概率神经网络(Probabilistic Neural Network，PNN)是基于贝叶斯决策理论的前馈型人工神经网络。其基本原理是通过应用贝叶斯决策规则，从多维空间分离出决策空间，根据分类误差期望最小化原则对训练样本进行模式分类。由于结合了径向基神经网络和经典概率密度估计理论，概率神经网络不像传统的多层前馈神经网络那样需要用BP算法进行误差反向传播计算，它训练时间短，不易产生局部最优，而且在数据样本足够多的情况下可以保证获得贝叶斯准则下的最优解。PNN的结构图如图1所示。

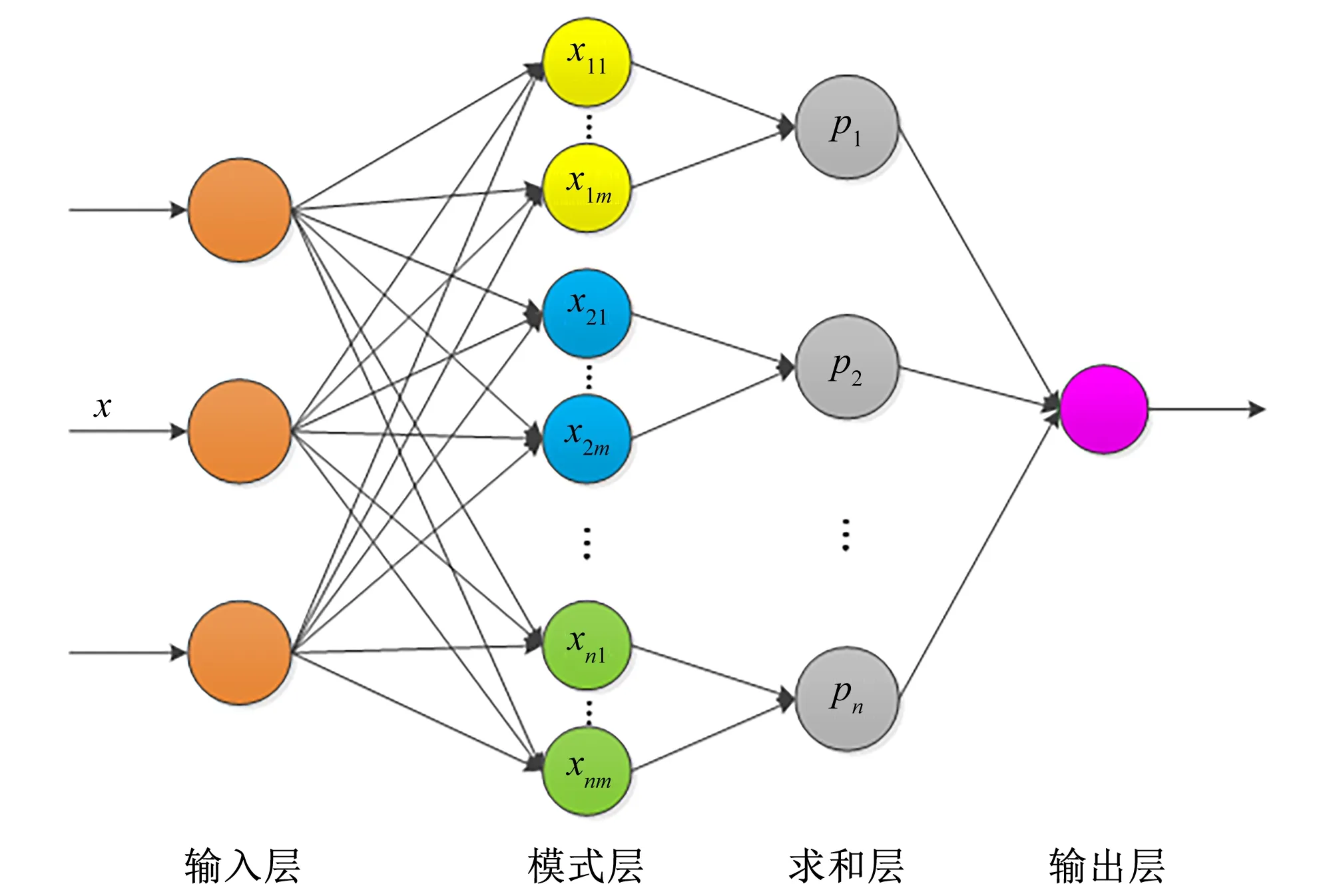
图1 PNN结构图Fig.1 PNN structure

PNN分为四层结构。分别是输入层、模式层、求和层和输出层。输入层负责接收训练样本的值，并将其传递至模式层，输入层神经元个数等于输入向量的长度。模式层通过连接权值与输入层相连接，该层负责计算输入训练样本的样本中心，并得出输入向量与样本中心的欧氏距离，通过激活函数得到输入向量与样本中心的相似度，每个神经元对应一个训练样本，该层神经元个数与输入训练样本个数相同。求和层负责将模式层各个类别的神经元相连接，该层神经元个数为训练样本分类个数。输出层负责输出分类识别结果。

在PNN中，模式层中第i类样本第j个神经元输入与输出的相似度表示为：

(7)

式中：x为样本输入向量；xij为模式层第i类样本的第j个中心；d为输入向量的维数；σ为最优平滑系数，对网络的性能有着至关重要的影响。

将模式层中属于同一类模式的神经元输出进行加权平均，得：

(8)

式中：vi(x)为输入向量x与PNN中第i类样本的相似度；L为第i类样本的个数。

最终取相似度最大的一类样本作为输入向量的判断类别：

y=arg max[vi(x)]

(9)

式中：y为输入向量经PNN后最终的输出类别。

3 基于改进不变矩与PNN的水电机组轴心轨迹特征提取验证分析

在相同运行状态下，水电机组的轴心轨迹形状基本相同，而不同运行状态下轴心轨迹的形状也会随之发生改变，如转子质量不平衡时轴心轨迹的形状为椭圆形，转子不对中时轴心轨迹的形状为外8字形，油膜涡动时轴心轨迹的形状为内8字形等。本文分别从构建仿真信号和机组实测信号两个方面对不同形状的轴心轨迹进行特征提取，并将提取的特征向量输入概率神经网络验证了分类效果。

3.1 模拟仿真实验验证

本文针对机组常见的故障，仿真生成了4种典型的轴心轨迹，如图2所示，其对应的机组运行状态分别为：油膜涡动(内8字形)、转子不对中(外8字形)、转子质量不平衡(椭圆形)、转子不对中和不平衡(香蕉形)，每种轴心轨迹各60组信号。为消除背景噪声对轴心轨迹形状识别的影响，本文运用多小波相邻系数降噪法[12]对轴心轨迹进行提纯，结果如图3所示。

图2 原始轴心轨迹Fig.2 Original shaft orbit

图3 降噪后轴心轨迹Fig.3 Denoised shaft orbit

结合离散情况下改进不变矩算法得出上述几种轴心轨迹的6个不变特征矩φ1～φ6，即可将这6个特征矩作为判别水电机组轴心轨迹的特征向量。不同轴心轨迹提取得到的不变矩特征向量如表1所示。

利用4种轴心轨迹的各60组仿真信号的特征样本创建PNN，每种类别选前30组信号作为训练样本输入，后30组作为测试验证，与预测分类结果进行比较，经训练确定式(7)中的最优平滑系数σ为0.01，分类识别结果如图4所示。

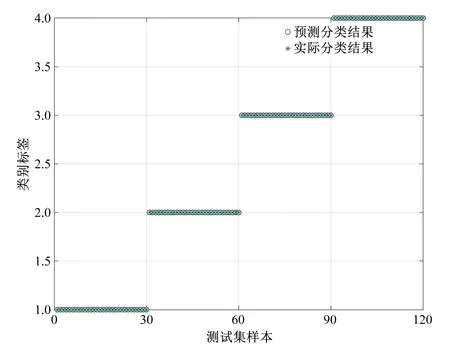
图4 改进不变矩特征向量经PNN后的分类结果Fig.4 PNN classification results of improved invariant moment vectors

从图4可以看出，4种轴心轨迹经改进不变矩算法所得到的特征向量的PNN分类均为100%，由此表明基于改进不变矩与概率神经网络的特征提取与分类方法对水电机组的轴心轨迹有着很好地识别与区分效果。

3.2 机组实测信号验证

已知S电站三号机组2015年8月发生掉转轮室里衬故障，转速为107.1 r/min，采样频率fx=458 Hz。本文选取该机组故障状态(以下简称“状态一”)以及经扩容改造后的正常状态(以下简称“状态二”)两种情况下的轴心轨迹进行分析，每种状态采集40组导轴承X、Y向摆度信号，合成的轴心轨迹图如图5所示。

表1 仿真模式下轴心轨迹的不变矩特征向量Tab.1 The characteristic moment vectors of shaft orbit under simulation model

图5 原始轴心轨迹Fig.5 Original shaft orbit

为消除机组运行时的背景噪声，运用多小波相邻系数降噪法对轴心轨迹进行提纯，结果如图6所示。

图6 降噪后轴心轨迹Fig.6 Denoised shaft orbit

结合离散情况下改进不变矩算法得出机组在两种运行状态下轴心轨迹的6个不变特征矩φ1～φ6，构建特征向量如表2所示。

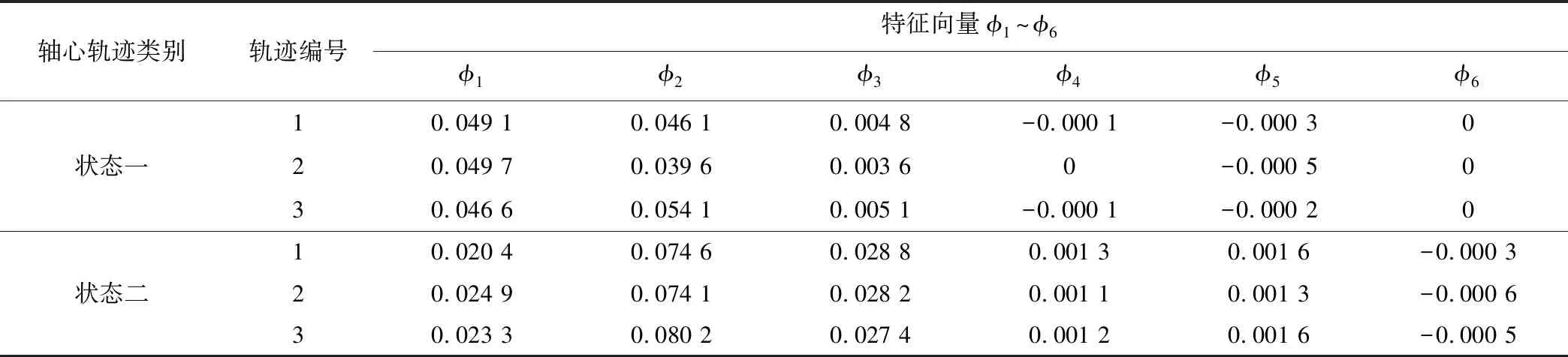
表2 实测模式下轴心轨迹的不变矩特征向量Tab.2 The characteristic moment vectors of shaft orbit under practical model

将不同状态下的轴心轨迹特征样本输入PNN进行识别分类，每种状态取前20组用于分类训练，后20组用于分类测试。得到的分类结果如图7所示。

图7可以看出，PNN对机组在两种运行状态下轴心轨迹的识别率为100%，充分表明了本文提出的基于改进不变矩与概率神经网络的特征提取与分类方法在水电机组轴心轨迹识别上有着很好的实际应用效果。

4 结 语

本文将图形处理中的改进不变矩与概率神经网络相结合，利用图形不变矩的平移旋转、伸缩不变性和概率神经网络训练时间短、分类准确的特性，对水电机组几种典型的轴心轨迹进行了识别与分类，同时结合机组实测数据进行了验证。结果表明，该方法能有效的识别水电机组不同形状的轴心轨迹，从而判别机组的不同运行状态，为水电机组的故障诊断提供有效的指导。

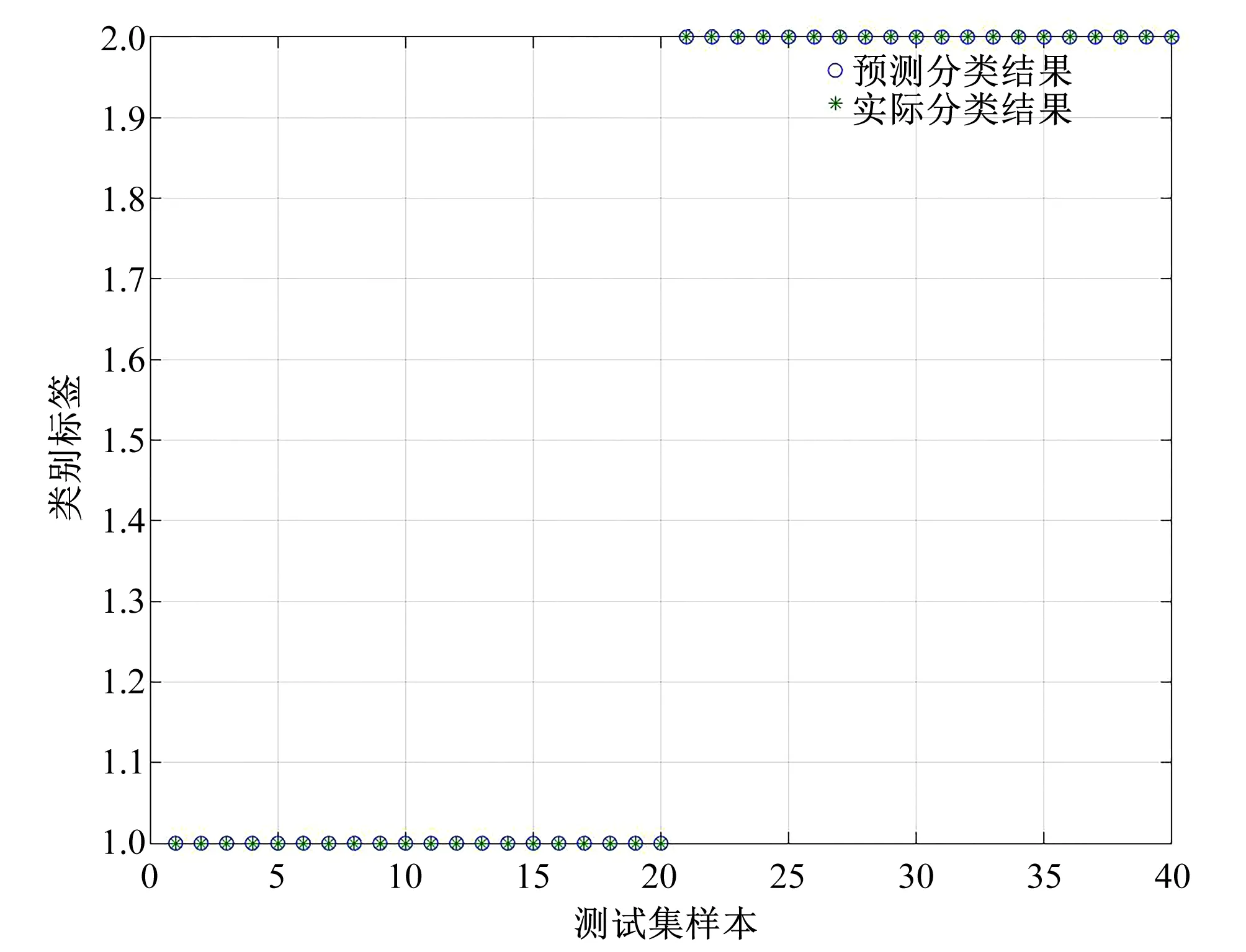
图7 改进不变矩特征向量经PNN后的分类结果Fig.7 PNN classification results of improved invariant moment vectors