一种高速重载码垛机器人误差分析
吴 振,万英和,吴连松,饶金海,武冰昕
(1.北京机械工业自动化研究所有限公司,北京 100120;2.北京万集科技股份有限公司,北京 100193)
0 引言
国产码垛机器人经过多年发展虽然取得了显著的成果,但是在末端定位精度上与国外码垛机器人相比还是有一定的差距,提高机器人末端定位精度主要途径是进行误差补偿,而误差补偿的理论基础是建立机器人末端位姿误差模型[1~3]。国内外许多学者在该领域做了大量的研究工作,并取得了许多成果[4~6]。童上高[4]等人,基于摄动法对沃迪公司的TPR-120/200码垛机器人进行了定位误差分析,并提出了各个可能引起末端位置误差的因素以及相应的误差补偿算法。宁凤艳[5]等人同样基于摄动法对MJR混联码垛机器人进行了误差分析,建立了其位姿误差模型,通过数值仿真分析了结构偏差,这种分析思路可以作为常用机器人误差分析方法。
本文基于D-H参数法建立码垛机器人构件间误差传递函数和手腕体末端位姿误差模型。综合考虑各个可能引起末端位姿误差的因素,从中提取对定位误差影响较显著的因素,研究其对位姿误差的具体影响,为码垛机器人加工、装配过程提供理论依据。分析机器人结构参数误差一定时,机器人末端位置误差随驱动关节转角的变化规律,之后研究了在重力作用下驱动关节柔性与杆件柔性对于末端误差的影响,并对不同位姿下的末端误差进行了计算。
1 建立码垛机器人误差模型
1.1 D-H参数法建模
基于D-H参数法[7],建立码垛机器人坐标系,如图2所示。其中静坐标系O0-X0Y0Z0固定在机架上,关节连接处建立各动坐标系,其中Zi轴均沿关节轴线方向,Xi定义为由Zi-1轴指向Zi轴方向。
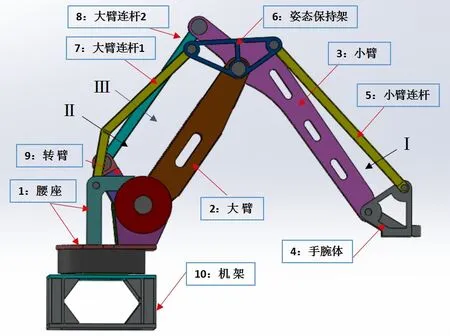
图1 码垛机器人三维示意图
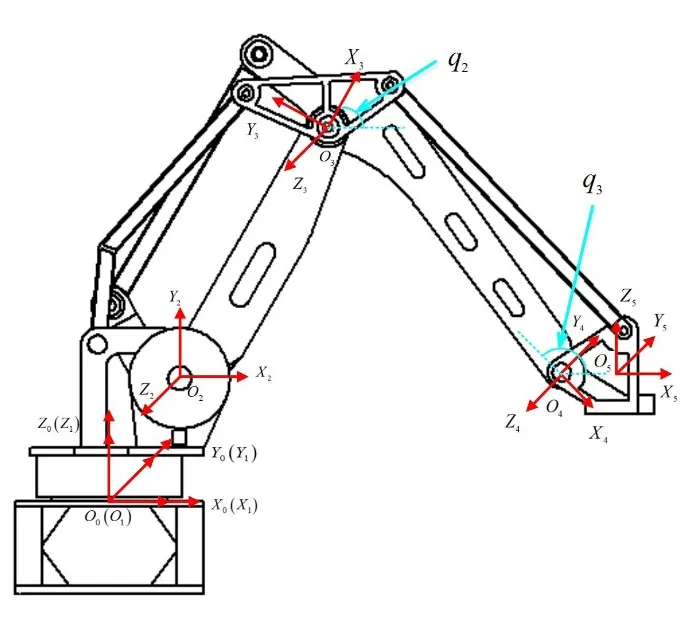
图2 基于D-H参数法的码垛机器人坐标系
构件结构参数以及理论值如表1所示,其中q1、q2、q3、q4分别表示腰座、大臂、小臂、手腕体四个驱动关节处的转角,同时。
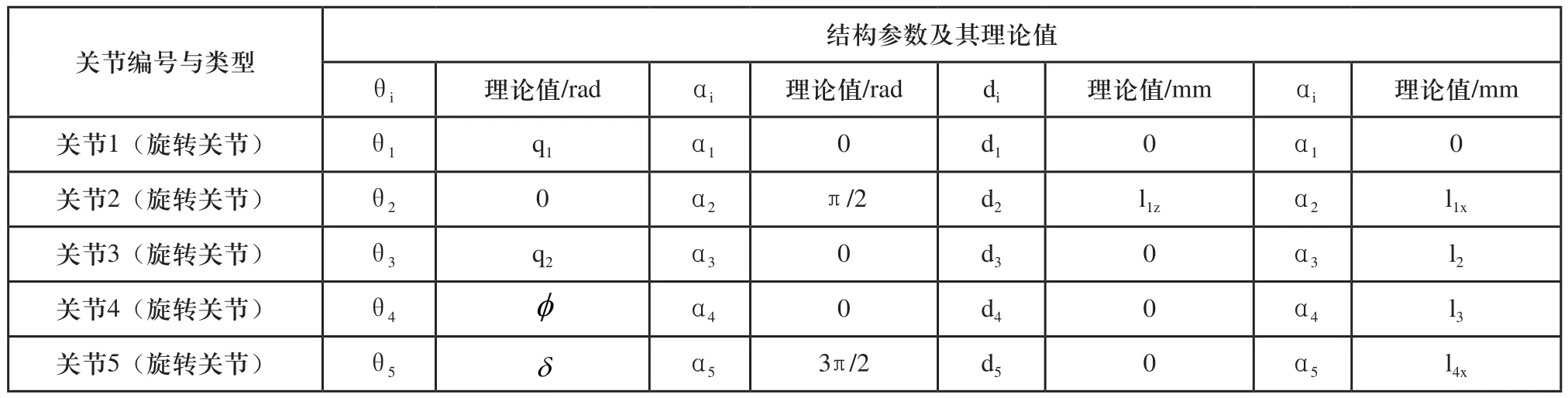
表1 机器人各构件结构参数及其理论值
根据D-H建模法得末端抓手位姿矩阵为:
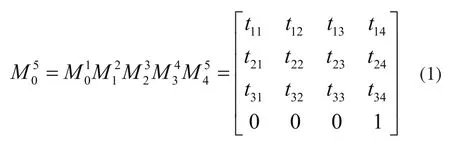
末端抓手静坐标系下位姿向量N为:

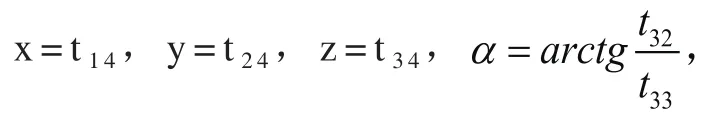
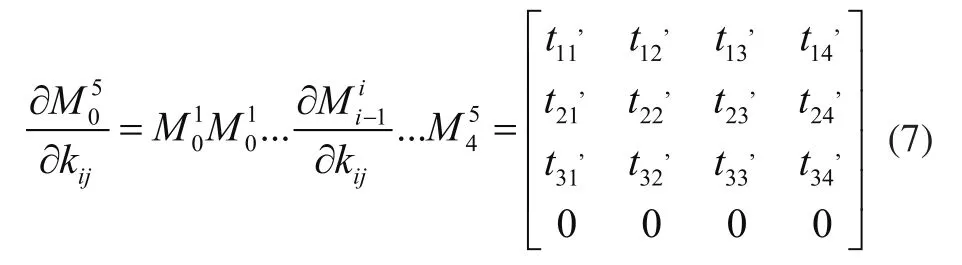
2.2 码垛机器人误差模型
码垛机器人各构件的加工、装配误差,机械传动误差等因素会导致各构件运动变量与结构参数产生误差,即:,进而最终影响末端手腕体的位姿误差。
相邻两构件之间的姿态变化矩阵对各结构参数的偏导,即位姿变换矩阵对θi、αi、ai、di偏导数为:


设ki1、ki2、ki3、ki4分别表示码垛机器人各构件的运动变量和结构参数码垛机器人末端的位姿矩阵对于kij(i=1,2,3,4,5;j=1,2,3,4)的偏导数可以表示为:
在静坐表系下的位置姿态误差,可以用向量ΔN表示:
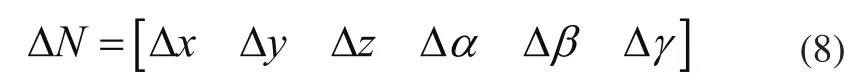
上式中,Δx、Δy、Δz为位置误差,Δα、Δβ、Δγ为姿态误差。结合姿态变化矩阵的偏导函数式(7)可得,位置误差函数与姿态误差函数:


至此,便得到了码垛机器人误差模型,基于码垛机器人误差模型可以对机器人各结构参数与运动变量的误差对机器人末端姿态误差的影响进行分析。
2 码垛机器人静态误差分析
本文重点研究零件制造、安装、机械传动误差造成的影响。暂不考虑重力、温度造成的零件变形误差与控制系统误差。在分析码垛机器人静态误差时假设机器人各构件均是纯刚体,忽略构件柔性与关节柔性对于末端变形的影响。本文主要考虑由于腰座、大臂、小臂、手腕体的加工、装配以及机械传动等因素造成的误差。此外姿态保持架与大臂连杆1和大臂连杆2的加工与安装误差也会造成末端位置姿态误差产生影响,本文重点考虑由于姿态保持架及相应连杆加工与安装误差对末端造成的平面度误差Δβ。
2.1 机器人末端位置误差分析
腰座、大臂、小臂、手腕体的加工、装配以及机械传动等因素造成的机器人末端位置误差,主要体现在各构件结构参数与运动变量参数误差造成的机器人末端位置误差。在各构件结构与运动变量参数一定的情况下,随着驱动关节角度变化,机器人末端位置误差也会随之变化。因此本节主要研究固定位姿下各构件结构参数与运动变量参数的误差对末端位置误差的影响,以及在结构参数与运动变量参数误差一定的情况下随着机器人驱动关节(大臂、小臂驱动关节)角度的变化,机器人末端误差的变化规律。
1)考虑各构件结构参数与运动变量对末端位置误差的影响。
首先给定码垛机器人位姿,设大臂驱动关节转角为45°,小臂驱动关节转角为135°,腰座驱动关节转角为0°。本文研究中为单一变量的误差对机器人末端位置误差的影响。
考虑腰座与机架关节处的3个结构参数α1、a1、d1与1个运动变量参数θ1存在的误差对末端位置误差的影响。首先分析腰座与机架关节处加工误差造成的a1与d1对末端位置误差的影响,如图3所示,其对末端位置误差没有放大效应,只是单纯的等比例误差影响。其次考虑由腰座加工与装配过程中产生的同轴度误差引起的Δα1以及腰座驱动关节误差引起的Δθ1对末端位置误差的影响,如图4所示。

图3 Δa1、Δd1对末端位置误差的影响
对于大臂与腰座关节、大臂与小臂关节、小臂与手腕体关节、手腕体与抓手关节处存在的其余16个结构与运动变量参数αi、ai、di、θi(i=2,3,4,5),在的其余16个结构与运动变量参数αi、ai、di、θi(i=1,2,3,4)对末端位置误差的影响,其分析方法与α1、a1、d1、θ1相同。限于文章篇幅有限,只分析某些对末端误差影响较大的参数。


图4 Δ1θ、Δ1α对末端位置误差的影响
腰座与大臂关节处,由于腰座加工与腰座、大臂装配过程产生的同轴度误差a2、Δθ2经大臂、小臂杆件放大作用后,对机器人末端位置Y轴方向误差产生较大影响,其影响规律如图5所示,对X轴与Z轴方向误差影响非常微小。由于腰座加工误差造成的a2与d2对末端位置误差没有放大效应,只是单纯的等比例误差影响。

图5 Δ2α、Δ2θ对机器人末端沿Y轴方向误差的影响
对大臂与小臂关节处,大臂与小臂关节处由于大臂加工过程与大臂、小臂装配过程产生的同轴度误差a3经小臂杆件放大作用后,对机器人末端位置Y轴方向误差产生较大影响,如图6所示。大臂与小臂关节处的运动变量误差(驱动关节产生的误差)Δθ3经小臂杆件放大作用后,对机器人末端位置X轴与Z轴方向误差均会产生一定的影响,如图6所示。大臂加工误差造成的d3对末端位置误差没有放大效应,只是单纯的等比例误差影响。
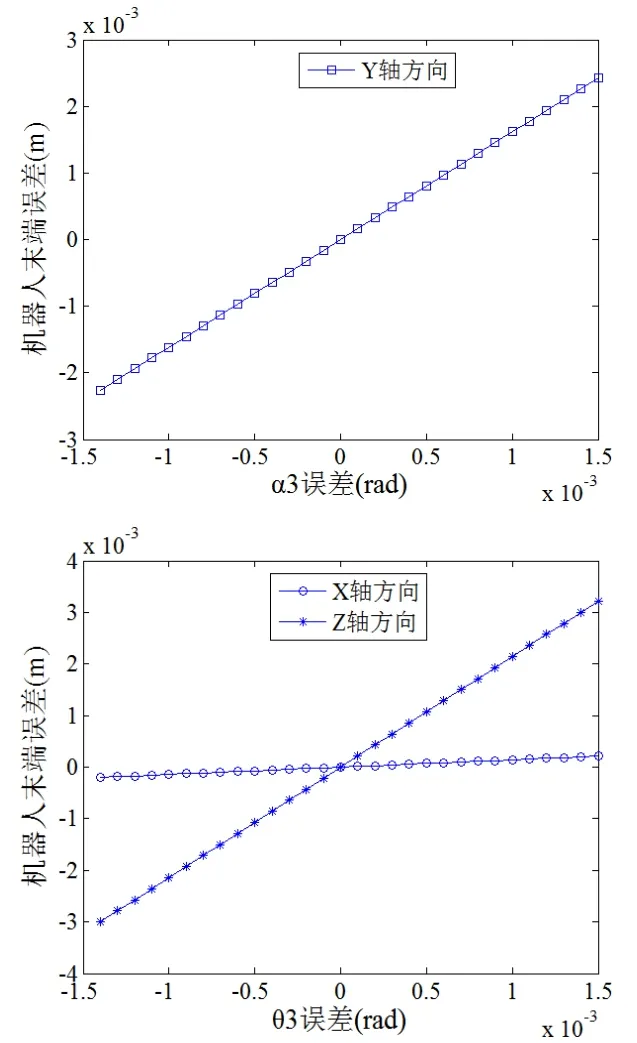
图6 Δ3α、Δ3θ对机器人末端误差的影响

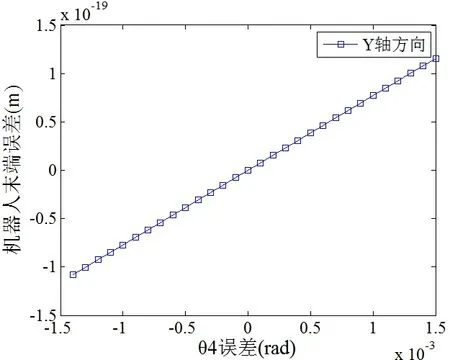
图7 Δ4θ对机器人末端误差的影响
考虑手腕体与抓手关节处的3个结构参数α5、a5、d5与θ5对末端位置误差的影响。由手腕体与末端抓手连接处加工误差引起的a5与d5对末端位置误差没有放大效应,只是单纯的等比例误差影响。由加工过程与装配过程中产生的同轴度误差引起的a5与Δθ5对末端位置误差很小,此处不再讨论。
2)考虑各驱动关节转角对末端位置误差的影响:
在各构件结构参数误差一定的情况下,考虑不同位置(各驱动关节转角不同)时,末端误差随驱动关节转角的变化规律。给定各构件结构参数误差:设ai、di的位移误差为0.05mm,设iα、θi的角度误差为0.5°。码垛机器人四个驱动关节中,腰座与手腕体驱动关节转角变化对末端位置误差没有影响。大臂、小臂驱动关节转角对末端位置沿Y轴方向误差影响成简单的线性关系,即随着码垛点距离机架位置越远,其末端位置沿Y轴方向误差越大;大臂小臂驱动关节转角变化对末端位置沿X轴与Z轴误差影响较为复杂。其影响规律如图8所示。

图8 大臂与小臂转角对末端位置误差的影响
由图8可以看出,在小臂转角一定时,随着大臂转角q2从0rad到2.4rad变化,末端Z轴方向误差先增大后减小,X轴方向误差线减小后增大;在大臂转角一定时,随着小臂转角q3从0.6rad到3.2rad变化,末端Z轴方向误差先一直减小,X轴方向误差线增大后减小;码垛机器人在大小臂运动过程中,其末端Z轴方向最大误差为7.68mm,其末端X轴方向最大误差为3.85mm。
2.2 机器人末端姿态误差分析
1)主要构件结构参数与运动变量误差对末端姿态误差的影响
由腰座加工与装配过程中产生的同轴度误差引起的Δα1,会对机器人末端沿X轴转动方向产生等效的误差Δα,对机器人末端沿Y轴与Z轴转动方向误差没有影响,如图9所示。由腰座驱动关节误差引起的Δθ1对末端位置误差的影响会对机器人末端沿Z轴转动方向产生等效的误差,对机器人末端沿X轴与Y轴转动方向误差没有影响,如图9所示。
在以改善生存条件和促进转型发展为特征的一系列试点示范基础上,随着我国经济社会发展和社会福利改进需求的调整,我国可持续城市建设逐渐从关注生存环境、经济转型发展等议题向关注社会的公平、人的发展公平以及社会与环境的协同发展方向转型,可持续城市关注的议题更加综合,更注重人与社会、人与自然、社会与自然的协调发展。
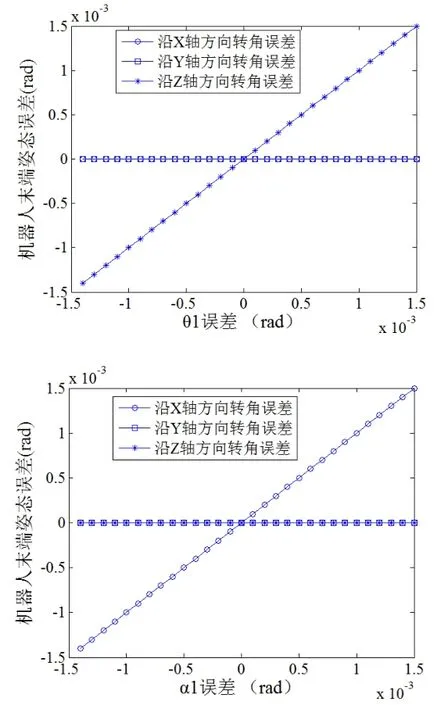
图9 Δ1α、Δ1θ对机器人末端姿态误差的影响
对于大臂与腰座关节、大臂与小臂关节、小臂与手腕体关节、手腕体与抓手关节处存在的其余8个结构与运动变量参数ai、θi(i=2,3,4,5)对末端姿态误差的影响,其分析方法与a1、θ1相同。
2)姿态保持架系统造成的姿态误差
码垛机器人结构简图,如图10所示。平行四边形ABFI与平行四边形BCDE的作用是保持手腕体下表面始终与地面平行。因此姿态保持架与姿态保持杆的加工与安装误差会造成的末端手腕体的平面度误差,即β。另外,姿态保持架与相应连杆的加工与安装误差也会对a、产生一定影响,因其影响较小,本文暂不考虑。
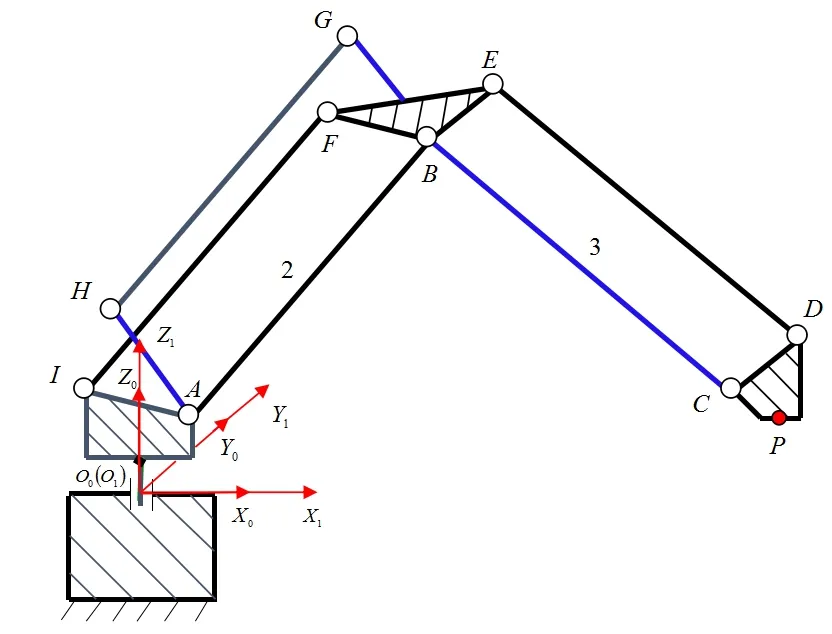
图10 机器人结构简图
考虑大臂连杆2与腰座连接处的I点加工位置或者安装位置误差对于手腕体末端平面度误差的β影响:设I为理论坐标点,设加工或者装配过程造成I点产生误差到I’点,根据杆长不变原理,可以求得F点的坐标:

由F点与B点坐标可以求解姿态偏差角:

上式中:θ表示AI连线与X轴的夹角(锐角)。
同理,可以求解由于F、E、D点处的加工位置或者安装位置误差对于手腕体末端平面度误差的β影响。
3 重力对机器人末端误差的影响
在前面分析机器人静态误差时,为了方便分析杆件单一结构参数对机器人末端位置姿态误差的影响,并没有考虑杆件以及关节的柔性。工程实践表明,码垛机器人在大负载情况下,重力造成的末端位置误差较大,不可忽略,因此本节重点研究重力造成的末端误差。在研究重力对码垛机器人末端误差的影响时,将机器人杆件作为柔性杆件,并且考虑驱动关节的柔性。
由码垛机器人整机运动微分方程[8,9]可得,静态下(各驱动关节角速度、角加速度为零)机器人在重力作用下的变形可以表示为:

其中:[K]表示291×291的系统刚度矩阵;{q}表示291×1的系统节点弹性位移;[G]表示系统所受的重力;
在重力作用下,码垛机器人末端沿静坐标系X轴方向误差以及沿Z轴方向误差可以表示为(设腰座驱动关节转角位零):

上式中:{q}67表示系统节点广义坐标系第67个坐标的弹性位移;{q}69表示系统节点广义坐标系第69个坐标的弹性位移;
码垛机器人系统刚度矩阵是与大臂、小臂转角有关的函数矩阵,系统刚度矩阵会随着大臂与小臂转角的变化而变化,即机器人在重力作用下末端误差会随着大臂与小臂转角变化而变化。在给定机器人各构件参数下,结合式(13)与式(14)可以求得不同驱动关节转角时,重力对末端位置误差的影响。随着大臂转角、小臂转角的变化,重力对机器人末端沿静坐标系X轴方向与Z方向的误差影响如图11所示。
由图11分析可知,在大臂转角一定时,随着小臂转角的增大,机器人沿Z轴方向误差先增大后减小;沿X轴方向误差,在机器人末端达到最远点之前,随着小臂转角的增大而增大,达到最远点之后,随着小臂转角的增大,沿X轴方向误差先减小后增大。

图11 重力造成的末端误差与大臂、小臂转角之间的关系
4 结论
本文主要对码垛机器人误差进行了分析,基于D-H参数法建立了码垛机器人误差传递函数;对机器人静态误差进行分析,重点研究了各构件结构参数对末端位置误差的影响,并对末端位置误差与关节转角的关系进行了分析。对机器人末端姿态误差,进行了研究,并对主要构件造成的误差影响进行了分析与讨论;建立了码垛机器人大臂、小臂静态驱动动力数学模型。对重力造成的末端误差,尤其是重力影响下导致大臂、小臂驱动关节转角误差对末端位置误差的影响进行了分析。为对应误差补偿提供了理论基础。

